不同饱和水汽压模型对GNSS反演可降水量的影响分析

李得宴,杨维芳,高志钰,4,李蓉蓉

(1.兰州交通大学 测绘与地理信息学院,兰州 730070;2. 地理国情监测技术应用国家地方联合工程研究中心,兰州730070;3. 甘肃省地理国情监测工程实验室,兰州730070;4. 中国地震局地质研究所,北京 100029)

0 引 言

水汽作为气象学和天气预报中关注的一个重要因素,其变化驱动着天气、气候产生相应的变化,同时也参与了地球气候系统的能量流动和水循环[1]．Bevis等[2]在1992年提出了基于GPS的大气水汽探测方法,为大气水汽探测提供了一种新方法．大气加权平均温度Tm作为地基全球卫星导航系统(GNSS)水汽反演过程中的一个重要变量,可以利用探空站资料通过数值积分的方法精确获得．但是计算Tm需要饱和水汽压Es参与其中,气象学研究中各研究人员建立了多种饱和水汽压模型,目前在国内地基GNSS水汽反演研究中计算饱和水汽压主要选取了其中的三种模型(Magnus-Tetens模型、BUCK模型、Goff-Gratch模型),查阅资料发现这三种饱和水汽压模型无论是结构还是计算结果都存在一定的差异,可能会对大气可降水量(PWV)的准确反演产生影响, 这将不利于不同研究人员研究结果的对比和气象数据的融合．所以本文以香港为研究区,利用上述三种不同的饱和水汽压模型计算饱和水汽压Es,通过数值积分的方法计算Tm;利用GAMIT解算得到了旱雨两季(2、7月)的天顶湿延迟(ZWD),然后利用Matlab编程模拟了由ZWD转化为PWV的过程．代入探空站数值积分求得的Tm和GAMIT解算得到的ZWD并最终计算得到每天的PWV,进一步对比三种不同饱和水汽压模型参与计算得到的Tm和PWV,最后分析这三种饱和水汽压模型是否均适用于地基GNSS水汽反演．由于在研究过程中发现部分研究人员将Buck模型中的变量T作为露点温度来进行相关研究,所以本文就这一问题进行了探究,并阐述了该做法的不合理性,这将为地基GNSS水汽反演中的部分研究提供参考．

1 GNSS水汽反演原理

1.1 PWV的计算步骤

在GNSS气象学中,利用GAMIT软件解算GNSS观测数据可以得到对流层天顶总延迟(ZTD),利用干延迟模型可以计算得到天顶对流层干延迟(ZHD),ZTD减去ZHD就可以得到对流层天顶湿延迟(ZWD)．

ZWD=ZTD-ZHD.

(1)

最后通过转换系数Π将ZWD转换为PWV．

PWV=Π×ZWD.

(2)

转换系数Π为

(3)

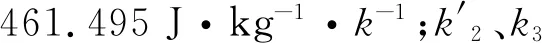
1.2 大气加权平均温度的计算

大气加权平均温度Tm的计算方法有以下三种方法:①常数法；②探空资料数值积分法；③模型法.本文将选择不同饱和水汽压模型在气温t下计算得到有差异的饱和水汽压值并通过数值积分(方法②)来计算得到不同的Tm，然后进行进一步计算、对比和分析。探空资料数值积分计算Tm公式为

(4)

式中，ei为传感器随探空气球上升过程中测得的第i和i+1层水汽压的平均值,但是水汽压e的值不能直接由传感器测量得到,需要通过测得的相对湿度RH和测得的第i和i+1层的平均温度Ti所对应的饱和水汽压值Es计算得到(如式5)．

(5)

式中：e为饱和水汽压；RH为相对湿度;Es为饱和水汽压.

2 饱和水汽压计算模型

饱和水汽压是定量的空气在给定的温度下所能保持的最大的水汽压,温度越高,空气达到饱和所需的水汽就越多．当水汽压高于饱和水汽压时,水汽将会凝结为小水滴．下面的三种模型是目前国内研究人员在地基GNSS水汽反演的研究中所采用的不同的饱和水汽压模型．

2.1 Magnus-Tetens模型

(6)

(7)

式(6)为相对于纯水面的饱和水汽压公式(适用温度为-45 ℃～60 ℃),一般情况下,水会在 0 ℃以下结晶成冰,但是研究发现纯水可以在-48 ℃时还以液态存在而形成过冷水,并且在层云和积云中存在过冷水,所以式(6)虽然为相对于水面的饱和水汽压公式,但将其温度适用范围扩展到0 ℃以下,使其也可用于过冷水状态下的饱和水汽压的计算[3-5]．式(7)为相对于纯冰面的饱和水汽压公式(适用温度为-60 ℃～0 ℃),式(6)、式(7)中,T为大气温度(℃),Esm代表该模型在相应温度下求得的饱和水汽压值(hPa),该模型由德国气象学家O. Tetens在1930年提出[6]．1967年Murray对其进行精度的评定,发现该公式精度较高,可以被应用于气象学中,但是其相对精度会随着温度的降低而降低[7]．文献[8-9]在地基GNSS研究的过程中均应用了该公式,但是在应用过程中并没有根据温度明确地区分应用水面、冰面公式,而是只用了相对于水面的饱和水汽压公式来计算探空气球上升过程中的每一层的饱和水汽压．

2.2 Goff-Gratch模型

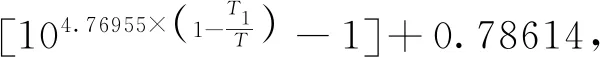
(8)

(9)

式(8)为相对于纯水面饱和水汽压公式(适用温度为0 ℃～100 ℃),式(9)为相对于纯冰面的饱和水汽压公式(适用温度为-100 ℃～0 ℃),式(8)、(9)中,Esg代表该模型求得的饱和水汽压值(hPa),T为大气温度(K),T1为水的三相点温度(273.16 K)．该模型由Goff和Gratch于1946年提出,Goff在1957年对该公式做了修订后被世界气象组织(WMO)作为计算饱和水汽压的推荐公式[10]．式(8)的适用温度为(0 ℃～100 ℃),但在WMO(2000)的技术规范中注明该模型在温度为-50 ℃的过冷水面上仍然可以使用,且误差极小[4-5,11]．但是由于该模型建立之初并未考虑过冷水状态,所以本文应用模型时该时仍以0 ℃作为分界点．文献[11-12]在地基GNSS水汽反演的研究中利用该模型来计算饱和水汽压,但仅应用了相对于水面的饱和水汽压模型来参与Tm的计算[12-13]．

2.3 BUCK模型

(10)

(11)

式(10)为相对于纯水面的饱和水汽压公式(适用温度为-45 ℃～60 ℃),所以式(10)也适用于过冷水状态下的饱和水汽压的计算,式(11)为相对于纯冰面的饱和水汽压公式(适用温度为-65 ℃～0 ℃),式(9)、(10)中,Esb代表该模型求得的饱和水汽压值(hPa);T为大气温度(℃)．该模型由Buck于1981年利用极小极大曲线拟合(Minimax fitting)法将不同温度区间的最大拟合误差最小化,进而得到该模型的最优系数[4-5,14]．文献[15-18]在利用数值积分法计算Tm时均使用该模型来得到所需的饱和水汽压值[15],但是目前在地基GNSS反演中应用该模型时,有大部分研究人员将T当作露点温度Td(℃)来计算[16-18],所以下面就该模型分别将T作为大气温度和露点温度的两种情况进行讨论,并对比这样的处理方式对Tm产生的影响,下文中把T当作露点温度来处理的BUCK模型称为BUCK 2模型．

3 研究区域及其方法

本文研究区域为香港,地处亚热带季风气候区,分旱雨两季,5—10月降雨较多,其余月份降雨较少[19]．香港king’s park探空站与香港地区卫星定位参考网中的昂船洲(HKSC)站相距约3 km,距离较近;海拔高度相差约40 m,地形起伏差异较小．一般情况下,利用GAMIT解算PWV时所用到的Tm都是通过建立的Tm模型来得到,但是为了避免建立模型环节带来的误差导致直接观察到不同饱和水汽压公式参与计算引起的PWV差异,本文近似地使用king’s park探空站的2016年旱(2月)雨(7月)两季高空气象数据计算得到的Tm来代替HKSC站进行解算时所用到的Tm．选取第二小节所述的不同饱和水汽压模型计算得到的饱和水汽压Es参与Tm的计算,将计算得到的不同的Tm分别应用到HKSC站点的GNSS水汽反演中并得到不同的大气可降水量PWV值,将king’s park探空站的PWV视为真值,对比在反演过程中不同饱和水汽压模型值参与计算得到的PWV值的差异,并分析差异存在的原因．探空站计算大气可降水量的公式如式(12)所示,式(13)为式(12)的数值积分式:

(12)

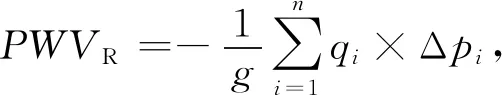
(13)

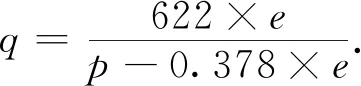
(14)

式中:g(m/s2)为地球重力加速度，m/s2;pi为不同高度观测层的气压,hPa;qi为不同高度观测层的比湿,g/kg,其计算公式为式(14);e为水汽压．

分别查阅香港天文台2013、2016版的香港气象及潮水观测摘要了解到,隶属于香港天文台的king’s park无线电探空站所使用的无线电探空仪是由芬兰Vaisala公司研发制造的．且该探空站在2006年7月之前使用Vaisala WS80型探空仪,2006年7月1日至2016年11月使用Vaisala RS92型探空仪,2016年11月至今使用Vaisala RS41型探空仪[20]．查阅Vaisala公司关于探空仪的技术支持报告,了解到Vaisala系统在计算饱和水汽压时采用了国际水和水蒸气性质协会 (IAPWS)于1995年推荐的饱和水汽压公式,如式(15)、(17)所示[21],式(15)为相对于水面的饱和水汽压公式(适用温度为0 ℃～373 ℃),式(17)为相对于冰面的饱和水汽压公式(适用温度为-100 ℃～0.01 ℃)．式(15)由A.Saul和W.Wagner于1987年提出,W.Wagner于1992年参照ITS-90(1990国际温标)进行了修订得到了式(15)[22],以下将式(15)、(17)简称为W.Wagner模型．

c4v3.5+c5v4+c6v7.5),

(15)

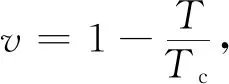
(16)

(17)

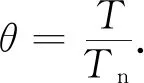
(18)

式(15)中：es为饱和水汽压;pc=22.064 hPa,为零界压力;Tc=647.097 K,为零界温度;T为大气温度, K; 系数c1=-7.859 517 83;c2=1.844 082 59;c3=-11.786 649 7;c4=22.680 741 1;c5=-15.961 871 9;c6=1.801 225 02;v的计算如式(16)所示．式(17)中,pn=6.116 57 hPa,为三相点温度的水汽压;系数a0=-13.928 169;a1=34.707 823,θ的计算如式(18)所示,其中T为大气温度,K;Tn=273.16 K,为水的三相点温度．

虽然在地基GNSS水汽反演的各研究中并未将式(15)、(17)应用到饱和水汽压的计算过程中,但是由于在对比时将香港king’s park探空站的PWV作为真值来参考,由上所述可知式(15)、(17)参与了探空站的PWV的计算,所以在下面的讨论中式(15)、(17)也将参与地基GNSS水汽反演过程中的Tm的计算,并和其他模型进行比较．

此次反演对比试验将会分别选择旱雨两季降水量差异较大的2月、7月份分别进行,且在基线解算时引入LHAZ、PIMO、SHAO、CUSV四个IGS站．IGS站、探空站、卫星定位参考网中的HKSC站的地理位置分布如图1所示．

图1 IGS站、CORS站、king’s park 探空站分布

4 不同饱和水汽压模型对Tm及PWV的影响

因为选择不同的饱和水汽压模型MT模型、GG模型、BUCK模型、BUCK 2模型、WW模型会首先影响大气加权平均温度Tm(下面的分析中将各不同饱和水汽压模型参与计算得到的Tm简写为Tm(MT)、Tm(GG)、Tm(BUCK)、Tm(BUCK 2)、Tm(WW)),进而影响PWV的反演精度,所以在讨论不同饱和水汽压模型对PWV精度的影响之前会先对比利用不同饱和水汽压模型计算得到的Tm的差异,再将GNSS最终反演得到的PWV值与探空站PWV值对比分析．

4.1 饱和水汽压模型的选取对大气加权平均温度(Tm)的影响

由于大气水汽几乎全部集中在气象学定义的对流层(0～12 km)内,所以在利用数值积分法计算Tm时仅采用探空数据中的大气高度为0～12 km记录的数据．通过分析香港地区2016年低温月份(2月)、高温月份(7月)在最接近大气层12 km处的温度发现:2月大气层顶最低温度为-56.5 ℃,最高温度为-44.5 ℃,平均温度为-49.9 ℃;7月大气层顶最低温度为-52.9 ℃,最高温度为-43.5 ℃,平均温度为-47.19 ℃．目前的地基GNSS水汽反演的研究中所采用的饱和水汽压模型以及香港探空站使用的Vaisala探空仪采用的W.Wagner模型已分别在第2、3小节中做了简略介绍,且由上述介绍可知Magnus-Tetens模型、BUCK模型的水面和冰面公式的适用温度范围存在重叠,文献[12]就存在以0 ℃作为冰、水面公式的分界点,还是以-45 ℃作为冰、水面公式的分界点的问题进行了实验验证,实验表明:利用探空仪测定的相对湿度计算水汽压时误用冰面饱和水汽压公式对对流层层顶(12 km左右)的影响在高精度需求中是不容忽视的[23]．世界气象组织(WMO)建议在0 ℃以下的相对湿度的测定应相对于水面,且Vaiaala探空仪在0 ℃以下的相对湿度的测定也是相对于水面的[24]．综上原因,本文在计算饱和水汽压时选择-45 ℃作为Magnus-Tetens模型、BUCK模型的水面和冰面公式的温度分界点．图2是由不同饱和水汽压模型计算得到2月、7月的Tm变化趋势图．对比图2中的(a)、(b)两张图可以看出,7月的Tm明显高于2月．单独分析图(a)、(b),可以发现在其余气象因子都相同的情况下,利用不同饱和水汽压模型通过式(4)数值积分计算得到的Tm变化趋势相同;但是由BUCK 2模型(以露点温度Td作为变量的饱和水汽压模型)参与计算得到的Tm与其他饱和水汽压模型参与计算得到的Tm相差较大,并且七月份的差异大于二月份．

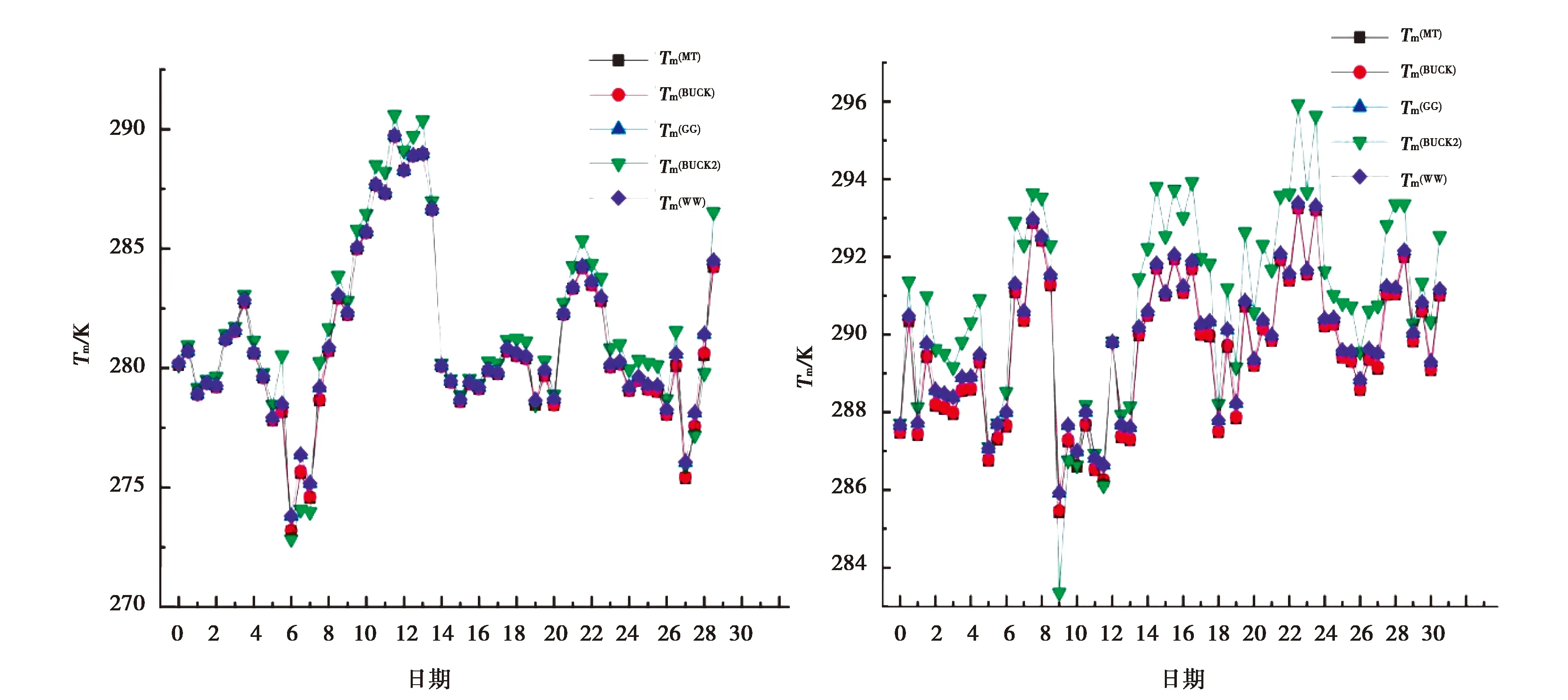
(a)2月份 (b)7月份图2 利用不同饱和水汽压模型通过数值计算法得到的香港2、7月份Tm变化趋势

各饱和水汽压参与计算得到的Tm月平均值m如式(19)所示,计算结果如表1所示．

(19)

式中：m为单个饱和水汽压模型参与Tm计算得到的Tm的平均值；Tmi为探空气球第i次升空探测并计算得到的Tm值；n为探空气球升空探测次数．

表1 不同饱和水汽压模型参与计算得到的香港2、7月份Tm的均值m K

通过图2中的(a)、(b)两张图及相应的表1可以看出Tm(BUCK)、Tm(MT)、Tm(GG)、Tm(WW)相差不大,一致性较好,但是Tm(BUCK 2)与其他的Tm值相差较大,存在明显的系统性差异．下面将结合图3所示的饱和曲线图分析这种较为明显的差异性的存在原因．图3的横轴为大气温度T,纵轴为饱和水汽压Es,红色曲线为饱和曲线,在饱和曲线上的水汽处于饱和状态,水的蒸发速率等于凝结速率,水在气态、液态两种状态之间的转换处于动态平衡．在曲线上的相对湿度为100%,所以此时的饱和水汽压等于实际水汽压(Es=e),且大气温度等于露点温度(T=Td)．相对湿度、饱和水汽压、水汽压的关系为

(20)

在曲线下方的区域A中,水汽处于不饱和状态,水的蒸发速率大于凝结速率,相对湿度小于100%,如果水汽压e不变,而想要处于A区域的不饱和状态3变为饱和状态2,就需要将状态3的温度(气温T)降低到状态2的温度(露点温度Td),使得饱和水汽压值Es的值降低,式(22)中的相对湿度RH就会达到100%,既水汽达到饱和状态．在曲线上方的区域B中,水汽处于过饱和状态,水的凝结速率大于蒸发速率,如果水汽压e不变,使处于B区域的过饱和状态1变为饱和状态2,就需要将状态1的温度(气温T)升高到状态2的温度(露点温度Td)．然而分析发现由king’s park探空站的探空仪所测得的相对湿度数据中只有个别值能达到100%,且相对湿度随探空仪高度的上升有下降趋势,所以由上述分析可知,探空仪上升过程所观测的水汽并没有全部达到饱和状态,而用露点温度Td作为BUCK饱和水汽压公式的变量,得到的就是水汽为处于饱和状态时的水汽压,就会高于实际值．所以就会导致Tm产生如上所述的明显差异,使得无论是Tm(BUCK 2)的平均值还是标准差都高于其他饱和水汽压模型参与计算得到的Tm．

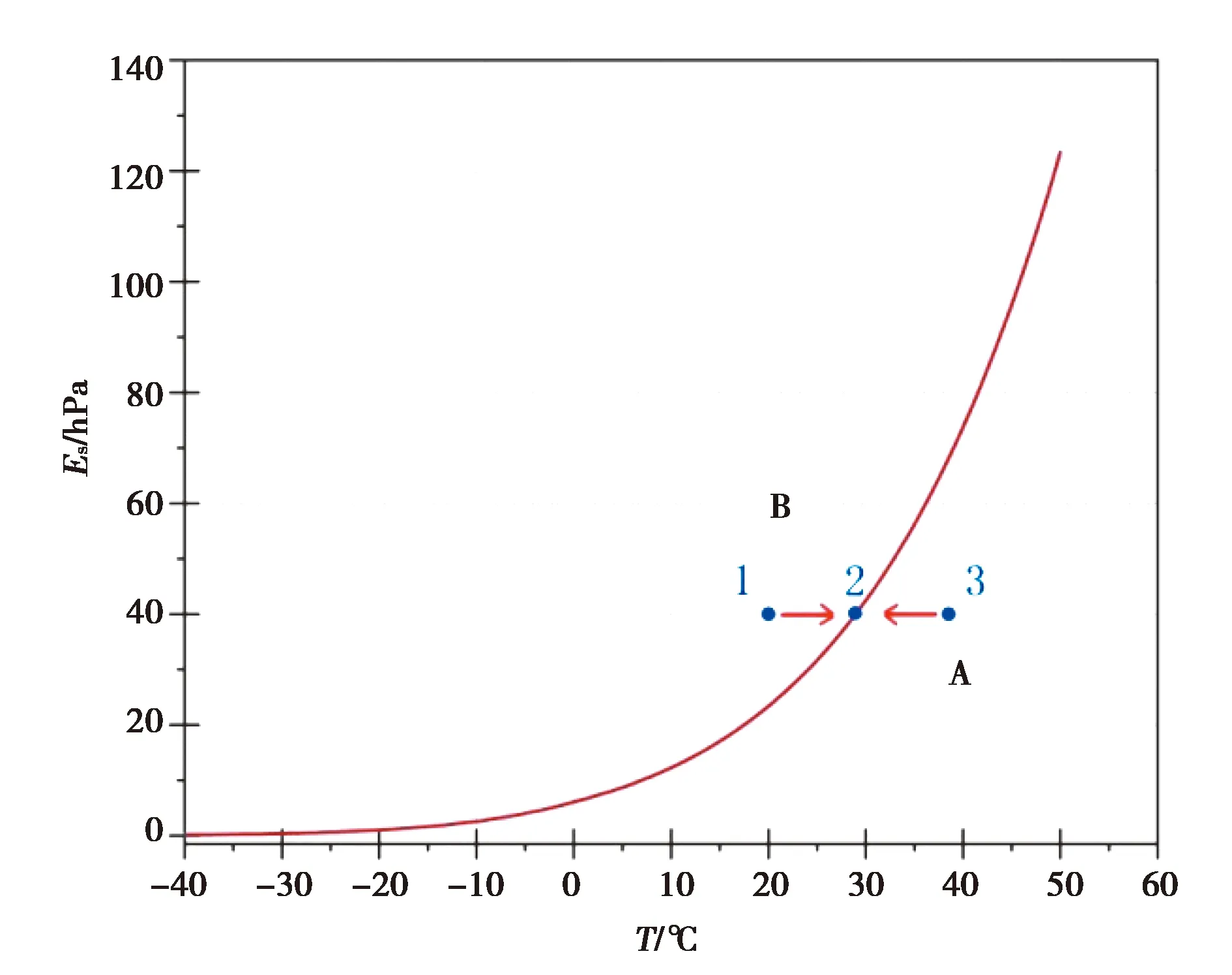
图3 饱和曲线

4.2 饱和水汽压模型的选取对PWV的影响

因为在GAMIT中为了一般化和方便大量计算,通常是利用文件中默认的以测站温度为变量的Bevis线性Tm模型或者是将其替换为较精确的本地化Tm模型来计算Tm,但为了避免建立模型环节带来的误差而导致直接观察不同饱和水汽压公式计算得到的值参与反演引起的PWV的差异,本文直接将距离HKSC较近的king’s park探空站所求得的Tm值作为计算转换系数Π时的输入值,只利用了GAMIT解算得到的湿延迟ZWD,将反演后续的转换系数Π及PWV的计算过程利用Matlab编程实现．且由上述分析,采用BUCK 2模型是不合理的,会引起较大的误差,所以在下面的PWV的对比分析中将不再讨论BUCK 2模型参与计算引起的PWV的差异．不同饱和水汽压模型参与计算得到的PWV的趋势图如图4所示(下面的分析中将各不同饱和水汽压模型参与计算得到的PWV简写(PWVMT、PWVGG、PWVBUCK、PWVWW):

由图4中的(a)、(b)图可以看出,GNSS反演得到的PWV的趋势与Radiosond探空站数据中PWV趋势一致,不同饱和水汽压参与计算得到的PWV差异较小．以探空站PWV数据为真值,计算了PWVMT、PWVGG、PWVBUCK、PWVWW的平均偏差(MEAN)、平均绝对误差(MAE)、均方根误差(RMSE),结果如表2、3所示.

(a)2月份 (b)7月份图4 2、7月份大气可降水量(PWV)趋势图

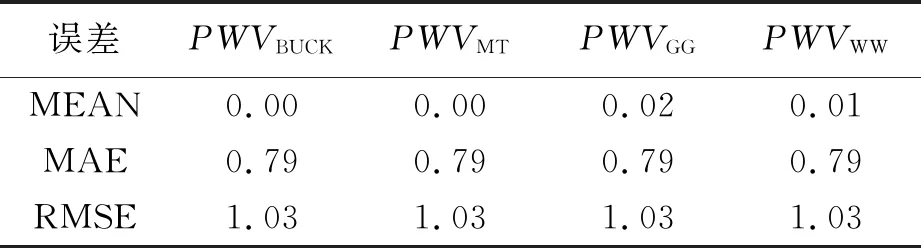
表2 2月份PWV精度验证 mm

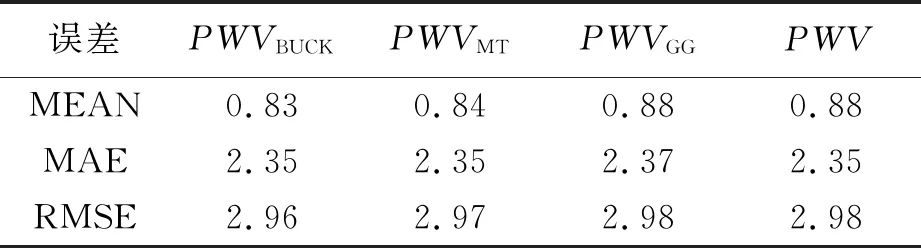
表3 7月份PWV精度验证 mm

进一步通过独立样本检验来研究讨论四种不同的饱和水汽压模型参与计算得到的PWV与探空站真值的差异性．在进行数据差异性检验之前,应先通过W检验(Shapio-Wik检验)来检验各组数据是否近似服从正态分布,然后再决定使用哪一种独立样本检验．当一组数据的W检验的显著性P值小于0.05时,否定原假设,认为该组数据不近似服从正态分布．结果表明,除7月的探空站PWV的W检验的P值为0.2明显大于0.05以外,其余各组数据的W检验的P值均小于0.05．说明除了7月的PWV(Radiosond)近似服从正态分布,2月、7月的其他组的PWV均不知道其分布状态,又因为Mann Whitney检验属于非参数检验,进行该检验前并不需要知道总体的分部情况,所以本文将采用Mann Whitney检验来判断两组独立的数据之间是否存在显著差异．该检验通过检验两组数据的均值是否存在差异来判断两个独立的样本是否存在显著差异,即若两个样本有差异,则他们的中心位置就会不同．当一组GNSS反演得到的PWV值与探空站的PWV值的Mann Whitney检验的显著性P值大于0.05时,接受原假设,认为反演得到的PWV与真值(探空站PWV值)不存在明显差异．2月、7月的GNSS反演PWV值与真值的Mann Whitney检验的显著性P值分别列在表4中.

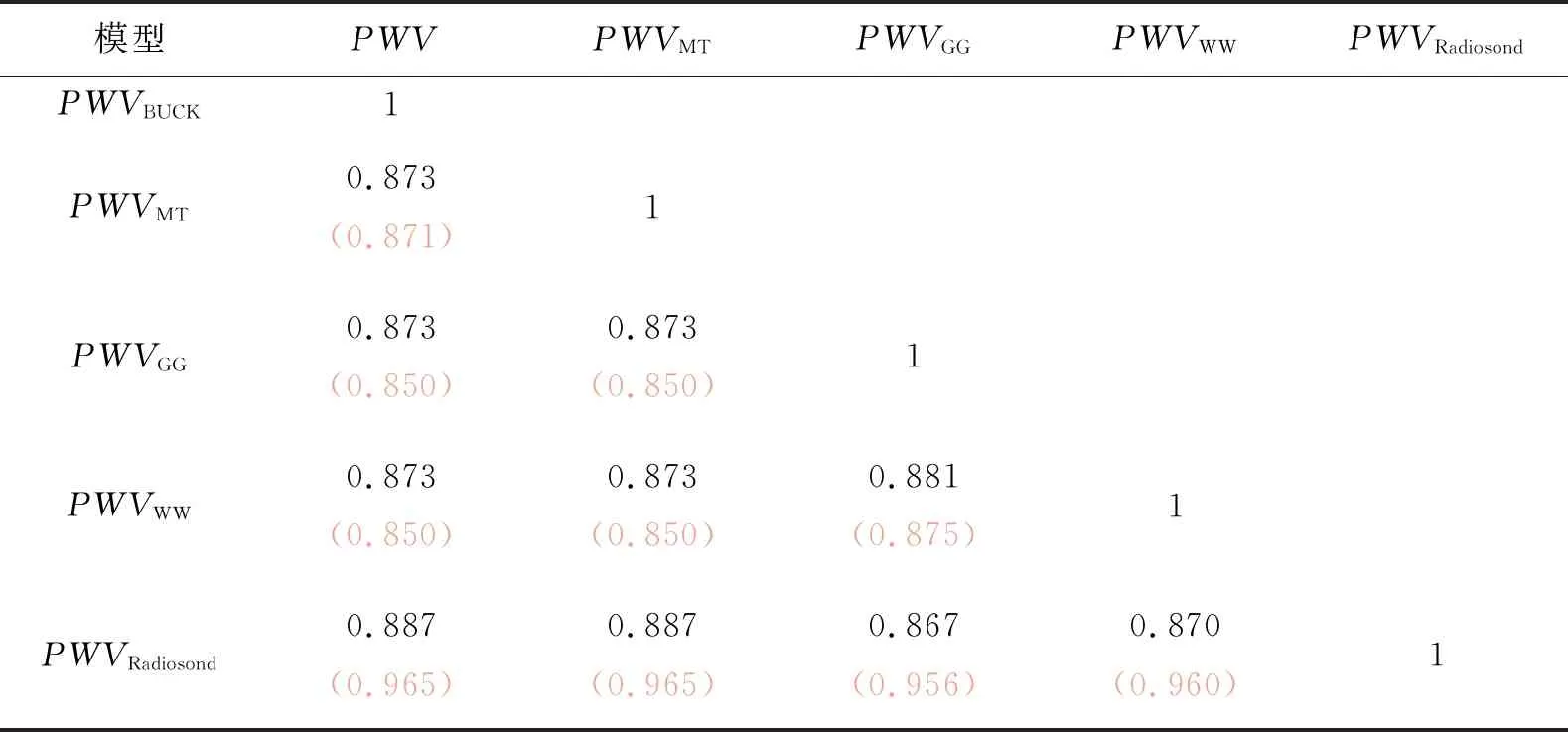
表4 Mann Whitney独立样本检验的显著性P值

由表3、4可以看出,2、7月的PWV反演精度都较高,且整体上2月份的PWV反演精度要高于7月份．但是反演得到的PWV的精度差异不大．在表5中,进一步通过Mann Whitney检验的显著性P值可以看出,无论是2月还是7月,显著性P值均大于0.05,所以可以进一步明确各不同饱和水汽压参与计算得到的PWV与真值之间不存在具有统计意义的显著性差异．这说明各饱和水汽压公式虽然存在形式和计算结果上的差异,但是该差异并没有使得GNSS反演得到的PWV值产生明显的不同．

5 结 论

本文针对目前地基GNSS水汽反演研究当中计算Tm的过程中所应用的三种不同的饱和水汽压模型,对比在反演过程中不同饱和水汽压模型参与计算得到的饱和水汽压值所引起的中间变量Tm和最终反演得到的PWV值的差异,评价这三种饱和水汽压模型能否较好地应用于地基GNSS水汽反演的研究中,得到如下的结论:1)Magnus-Tetens模型、Buck模型、Goff-Gratch模型应用在地基GNSS水汽反演过程中都能得到较好的反演精度,且利用三个不同模型反演得到的PWV值的差异性也较小．利用Vaiaala探空系统采用的饱和水汽压模型参与GNSS水汽反演得到的PWV值和中间值Tm与上述三种模型参与计算得到的值有很好的一致性．所以利用数值积分求Tm值并用来建立Tm模型时,这三个不同的饱和水汽压模型都可以被用来提供计算样本Tm时所用到的饱和水汽压．2)在使用BUCK模型时,误将T作为露点温度来计算饱和水汽压是不科学、不合理的,将会产生较大的误差,所以以后的研究中在使用该公式计算饱和水汽压时,应该将T当作大气温度,才能利用BUCK模型得到合理的饱和水汽压值,进而应用到GNSS水汽反演过程中．