星载加速度计校准对GRACE轨道动力学平滑的影响分析

高松涛,游为,范东明,余彪,生永赟

(1.西南交通大学 地球科学与环境工程学院,成都 611756;2.广东省交通规划设计研究院股份有限公司测量部,广州 510507)

0 引 言

近年来,基于星载GPS技术进行低轨卫星精密定轨的研究取得了很大的进展,根据是否采用低轨卫星所受的摄动力模型及与力学模型的关系,可以将定轨方法分为运动学(或称几何学)定轨、动力学定轨和简化(或称约化)动力学定轨[1-5]．

国内外学者均对星载GPS卫星定轨做了深入研究．Yunck[6]等提出不依赖动力学模型的方法,完全基于星载GPS观测值进行定轨,即几何法定轨．Schutz[7]等采用动力学定轨得到连续的轨道,但是轨道精度受力模型精度的影响比较大．接着,Yunck和Wu[8]等又提出一种把动力学模型信息和几何观测值按一定权重结合起来的动力学定轨模型,称为约化动力学法．Bertiger[9]等利用美国航空局(NASA)和法国国家空间研究中心(CNES)联合发射的海洋卫星TOPEX/Poseidon,得到其实际径向定轨精度为3 cm．在国内,对星载GPS定轨方法的研究也取得了一定的成果．李建成等[10-12]对GRACE卫星进行了轨道计算,并与美国喷气推进实验室(JPL)提供的事后精密星历进行比较,GRACE-A卫星单天非差运动学轨道的径向精度为3～4 cm,GRACE-B为3～5 cm．郭金运和孔巧丽等[13-16]采用动力学法对HY-2A卫星进行SLR、DORIS精密轨道仿真,发现动力学定轨精度均在厘米级．吴林冲[17]分析了点火脉冲对加速计校准结果的影响,得到其对校准结果的影响在X、Y、Z方向上高达10-10m·s-2．

在动力学定轨中,卫星所受的摄动力对于轨道的影响较大,以上学者在以加速度计代替非保守力摄动的方法中,通常只估计加速度计三个偏差和三个尺度参数,没有详细分析各种尺度和偏差参数,以及估计时间对轨道的影响[10-11]．

1 定轨策略

首先建立卫星运动的摄动力方程,通过对初始轨道和先验摄动力模型数值积分得到积分轨道作为参考轨道,然后求解卫星轨道相关偏导数[18-22]．

1.1 动力学定轨理论

动力学法定轨的基本原理是将卫星位置和速度视为卫星所受摄动力和卫星初始状态以及时间的函数,即

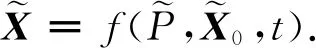
(1)

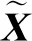
1.2 参数估计策略

SuperSTAR加速度计作为GRACE卫星关键有效荷载之一,安装在GRACE卫星的质心上,用来测定作用于GRACE卫星的非保守力．在卫星运行过程中,仪器本身的物理特性和外部摄动力作用使得加速度计观测数据产生了偏差和尺度因子变化[23-26],将加速度计校准参数引入卫星动力学模型中,以加速度计测量值代替非保守力模型

(4)

引入加速度计校准参数并将非保守力转换至惯性系中

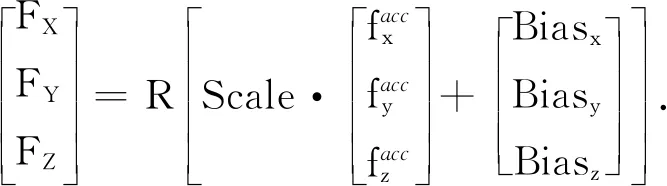
(5)

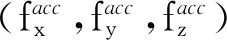
1.2.1 偏差参数模型

(6)

式中：Ci为偏差系数;ΔTi为待估的时间到参数作用起点的时间差;N为所选偏差模型的阶数．

1.2.2 尺度参数模型

1) 对角阵常量尺度模型

(7)

式中:SX、SY和SZ分别代表切向、法向及径向的尺度参数,影响加速度分量在切向、法向、径向的大小[20].

2) 全矩阵尺度模型

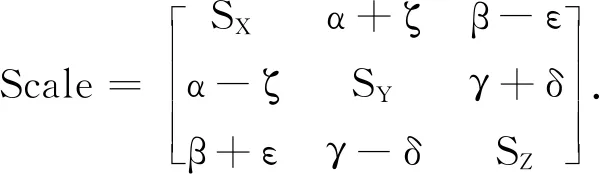
(8)

式中:α、β与γ为对称剪切参数,表示加速度计轴非正交性之间的关系;ζ、ε与δ为斜对称旋转参数,表示科学参考框架(Scientific Reference Framework)与加速度框架(Acceleration Framework)之间的未对准误差[20,27].

2 不同估计策略下的轨道平滑结果

分析

本文先以JPL发布的2009年5月1日的约化动力学轨道数据作为观测值,采用动力学方法进行轨道平滑,在优化先验背景场和每弧段卫星初始状态的过程中,积分弧长为24 h,卫星初始状态每弧段校准一次,摄动力模型的优化主要为加速度的校准即尺度改正和偏差改正．

2.1 不同的时间估计策略

首先，分析加速度参数的估计时间对轨道平滑的影响.由于尺度模型和偏差模型对轨道误差的敏感性不同,尺度参数的估计策略为每弧段估计一次,偏差参数对于轨道加速计的影响较为明显,不同的估计时间会有明显的差异,故以偏差参数的估计时间为基准来分析时间对其影响.因积分弧长为24 h,设置偏差参数的估计时长由长到短分别为12 h、6 h、4 h、2 h、1 h、15 min和12 min,分析估计时间对轨道平滑的影响,并实验得到不同估计时间下所对应最佳的偏差模型,如表1所示，图1～7为不同偏差参数估计时间下的轨道平滑残差图．

表1 不同偏差参数估计时间对应的估计策略

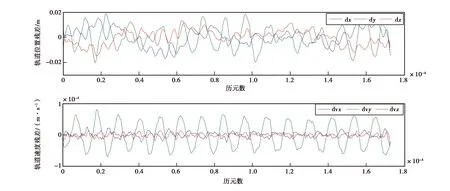
图1 采用12 h估计策略得到的GRACE卫星2009年5月1日积分轨道与JPL发布的约化动力学轨道的残差

图2 采用6 h估计策略得到的GRACE卫星2009年5月1日积分轨道与JPL发布的约化动力学轨道的残差

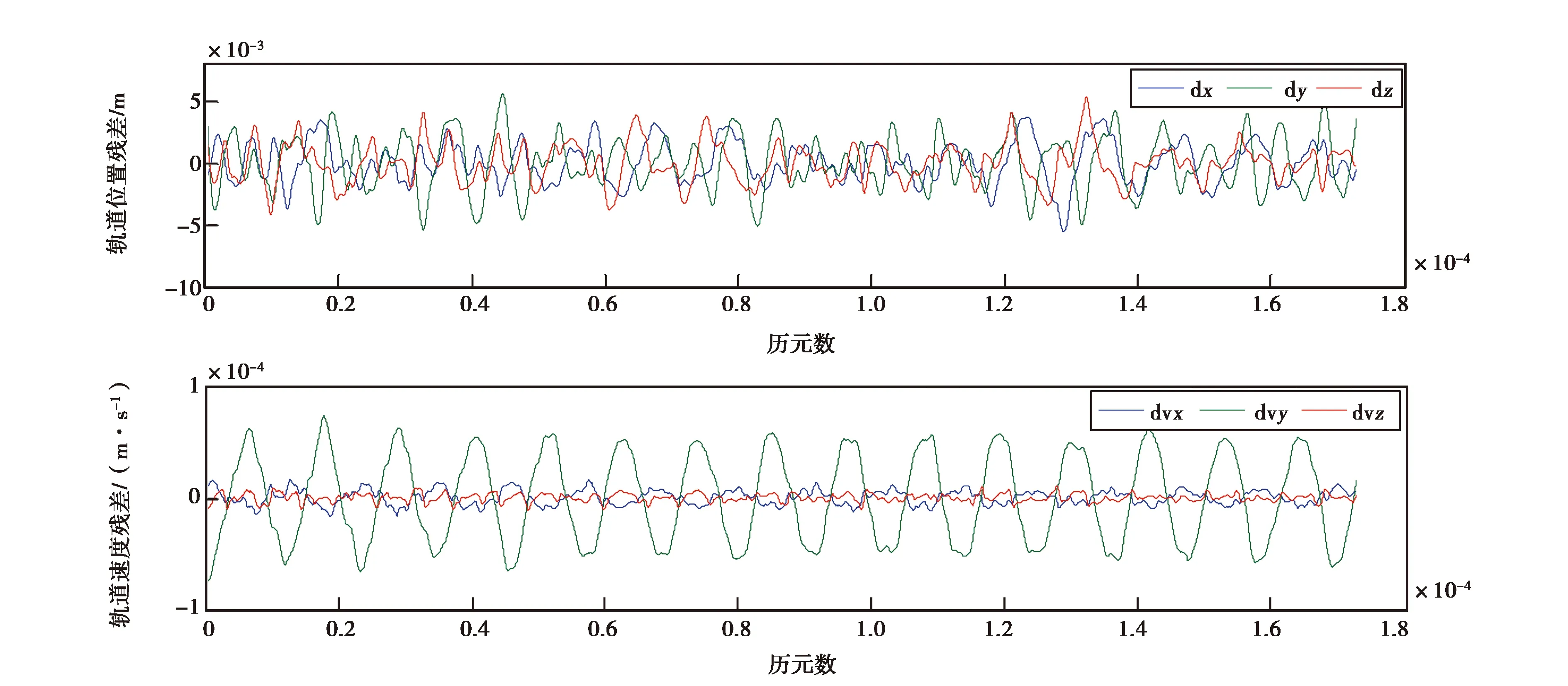
图3 采用4 h估计策略得到的GRACE卫星2009年5月1日积分轨道与JPL发布的约化动力学轨道的残差

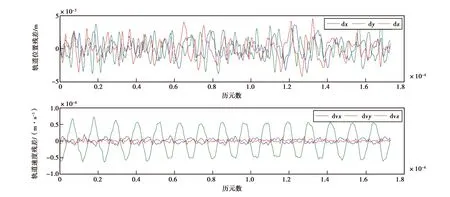
图4 采用2 h估计策略得到的GRACE卫星2009年5月1日积分轨道与JPL发布的约化动力学轨道的残差

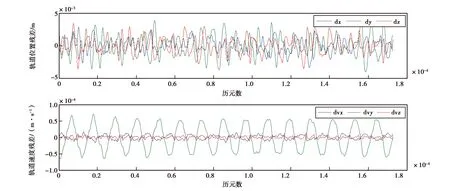
图5 采用1 h估计策略得到的GRACE卫星2009年5月1日积分轨道与JPL发布的约化动力学轨道的残差

图6 采用15 min估计策略得到的GRACE卫星2009年5月1日积分轨道与JPL发布的约化动力学轨道的残差

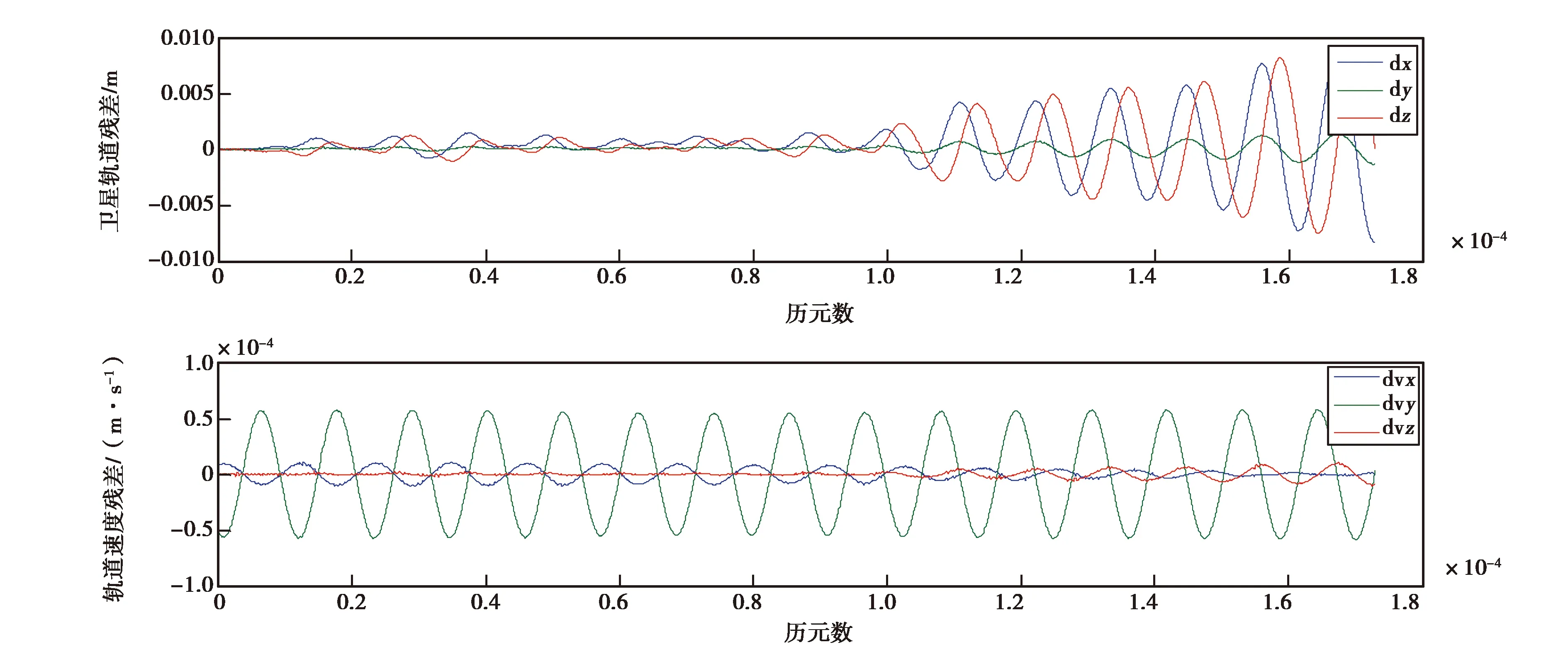
图7 采用12 min估计策略得到的GRACE卫星2009年5月1日积分轨道与JPL发布的约化动力学轨道的残差

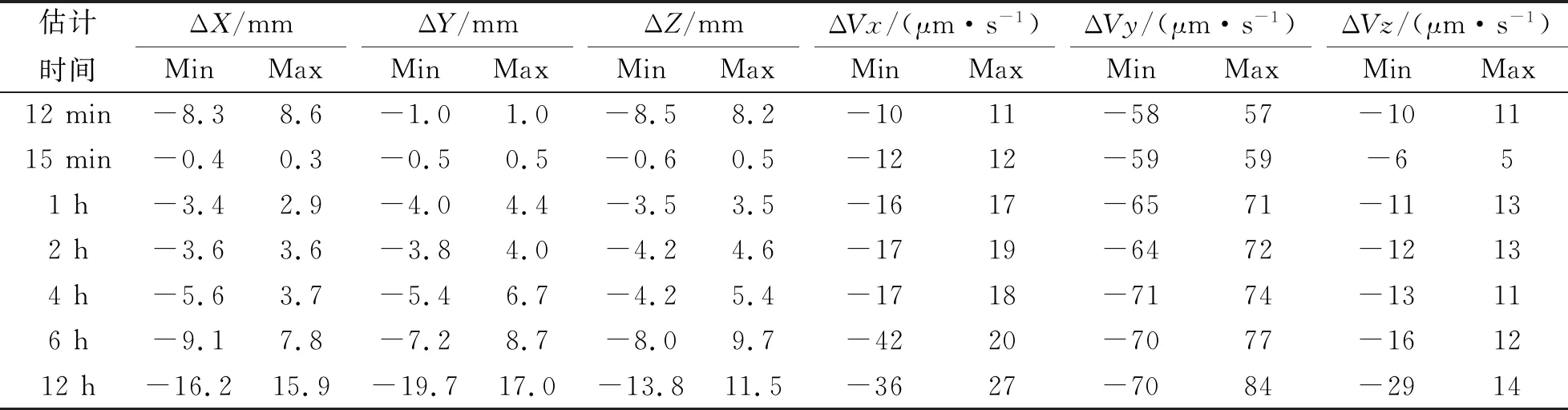
表2 不同偏差参数估计时间得到的轨道位置和速度残差

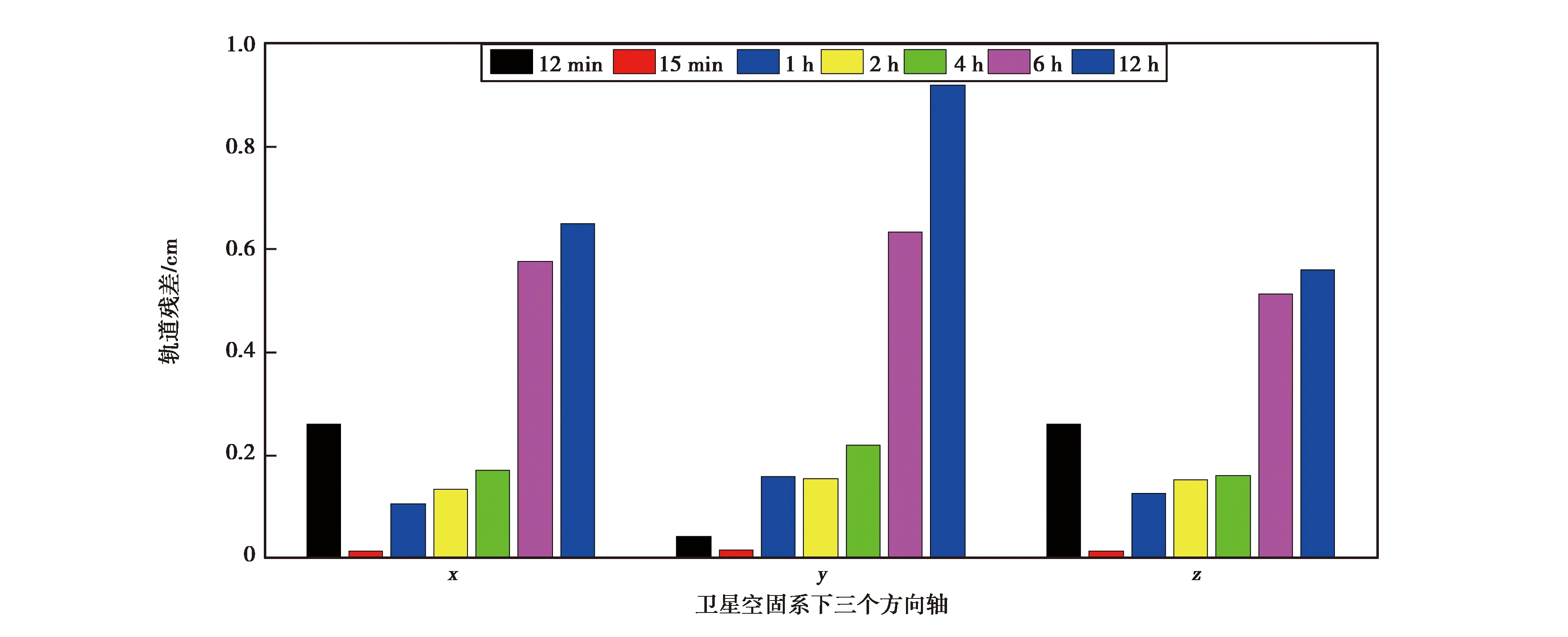
图8 不同时间估计策略对应GRACE卫星轨道残差分析

表1～2分别表示偏差参数在不同估计时间对应的策略、平滑后的轨道位置和速度残差,由图1～7不同策略对应的轨道残差图可知,当偏差参数估计时间分别为12 min、15 min、1 h、2 h、4 h、6 h和12 h时,得到三个方向上所对应1天的轨道残差的范围分别为:-0.85～0.86 cm、-0.06～0.05 cm、-0.40～0.44 cm、-0.42～0.46 cm、-0.56～0.67 cm、-0.91～0.97 cm、-1.97～1.59 cm．可知偏差参数估计时间大于15 min时,随着估计时间增加得到平滑后的轨道在X、Y、Z三个方向的轨道残差逐渐增大,可见偏差参数的估计时间对轨道平滑的影响明显,估计时间的缩短可很好地吸收摄动力模型的误差．尺度和偏差参数都是时间的函数,随着估计时间由12 h至15 min,同弧段偏差参数估计量由20增加到192个,使得每弧段卫星初始状态和先验背景场更逼近真值,得到的平滑轨道精度更高．当偏差参数估计时间为12 min时如图7所示,轨道残差在X方向、Y方向和Z方向随着积分时间逐渐增大,此时法方程解算过程存在病态问题,造成解算轨道不可靠．由图8看出,估计时间大于15 min时三个方向的轨道均方根(RMS)值也随着估计时间的增加而增大,且Y方向RMS值大于另外两个方向的RMS值,原因可能在于科学参考框架(SRF)下Y方向上的非保守力对轨道的影响没有其他两个方向敏感,因此参数估计时Y方向校准参数精度也最差,得到的轨道残差也相对较大．

12 h和15 m的偏差模型分别采用高阶多项式和低阶多项式去估计,轨道残差如图1和图6所示,残差范围分别为±2 cm和±0.05 cm．低阶多项式短时间估计和高阶多项式长时间估计各有优缺点,以高阶多项式长时间估计策略的优点是参数相对较少,法方程相对稳定[26],以低阶多项式短时间估计策略的优点是可以估计出一些高频的误差,得到轨道精度较高．

2.2 不同的尺度模型

对于加速度的校准中尺度参数和偏差参数对于时间是敏感的．在2.1的基础上,本节主要分析如何选择合适的尺度模型使动力学平滑后的轨道精度更高．当偏差参数估计时间固定时,以不同的尺度模型为变量进行实验来分析其平滑后的轨道残差,如表3所示.平滑结果如图9～11所示.

表3 不同尺度模型对应的估计策略

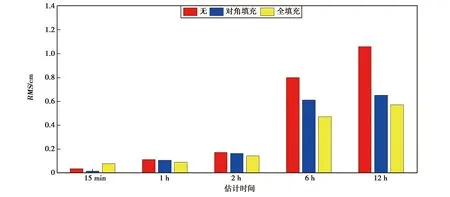
图9 不同时间估计区间下，三种尺度模型积分轨道所对应的X方向的RMS

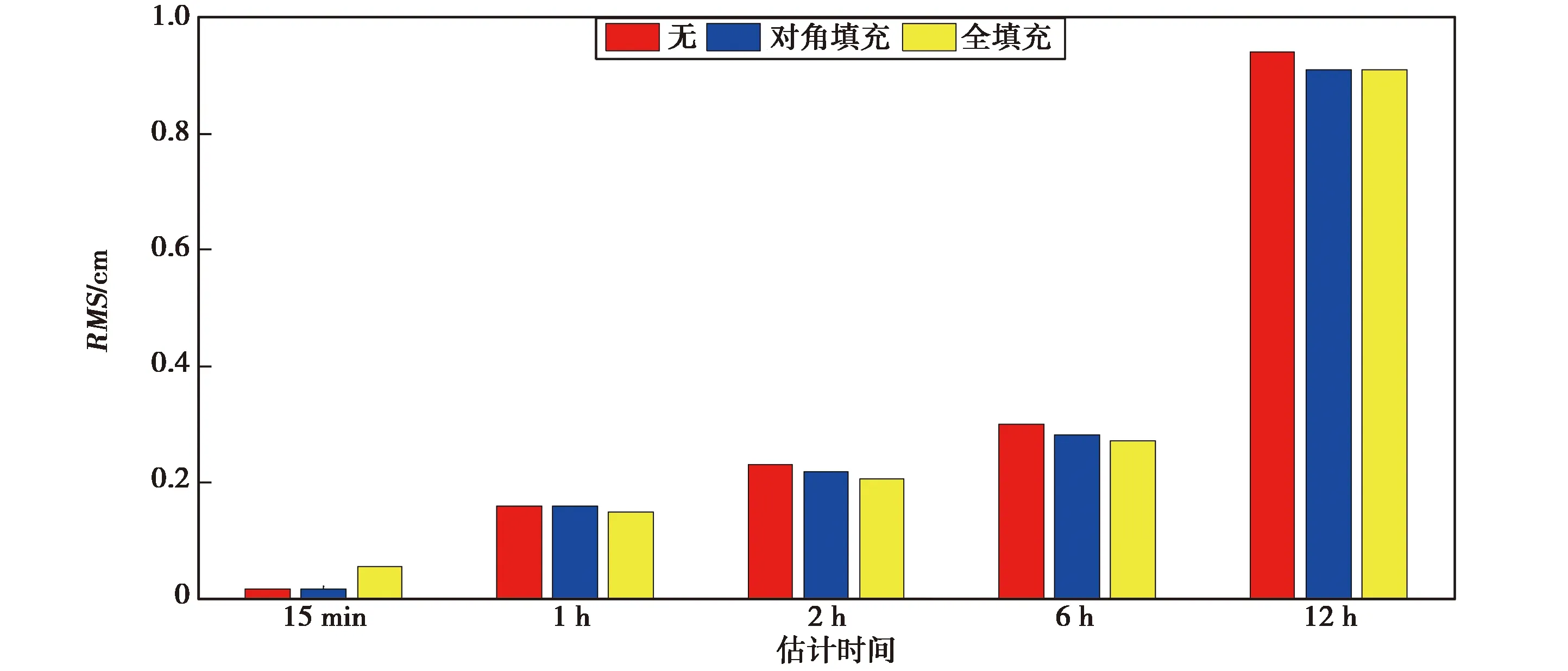
图10 不同时间估计区间下，三种尺度模型积分轨道所对应的Y方向的RMS

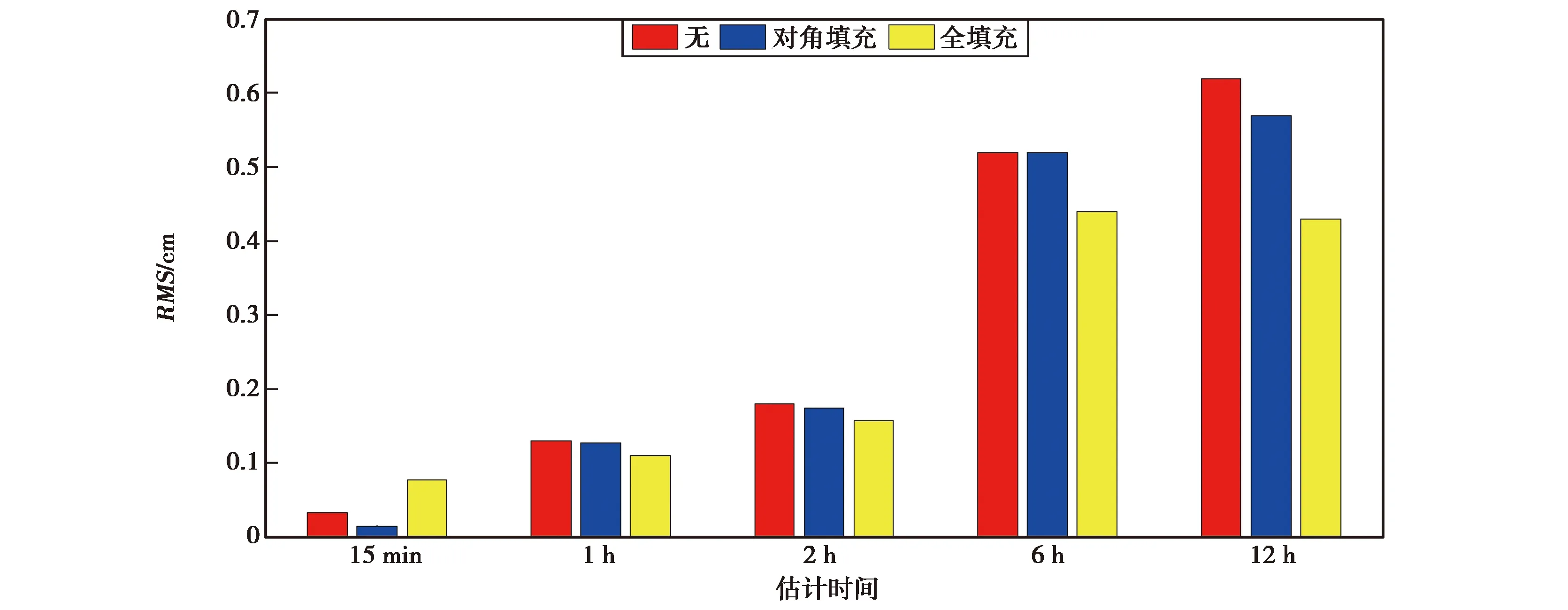
图11 不同时间估计区间下，三种尺度模型积分轨道所对应的Z方向的RMS

图9～11分别为X、Y、Z方向上不同偏差参数估计时间下三种尺度模型所对应的轨道RMS值,由图10可知:在偏差参数估计时间为15 min、1 h、2 h、6 h和12 h时,尺度模型的设置对轨道Y方向影响较小,如估计时间为12 h的轨道在Y方向RMS值在三种尺度影响下分别为0.94 cm、0.91 cm、0.91 cm;估计时间2 h轨道在Y方向的RMS值分别为0.23 cm、0.22 cm和0.21 cm;由图9～11可知在偏差参数选择估计时间时,尺度模型对于积分轨道的影响较小,且其影响小于偏差参数估计时间对轨道的影响．当估计时间为15 min时,不考虑尺度模型和对角填充的尺度模型的RMS值小于全填充的尺度模型,尺度模型的设置主要校准加速度计安装误差所导致的加速度轴的非正交性[20,27],在加速度校准过程中尺度参数为每弧段24 h估计一次,当偏差参数估计时间较为频繁时,对于尺度参数的校准会产生影响,故尺度参数不能频繁的估计．估计时间较长时应采用全填充的尺度模型,估计时间较短可采用对角填充的尺度模型或不考虑尺度参数的影响．

3 对ITSG发布的几何轨道进行分析

采用ITSG发布的几何轨道作为观测数据,来探究以上实验方法的可行性,并对结果进行详细分析．上述结论中,得出采用15 min间隔的偏差估计策略得到的轨道与JPL发布的约化动力学轨道残差和RMS值最小,采用该策略对GRACE几何轨道进行处理,几何轨道经不同处理后与JPL发布的约化动力学轨道比较残差,如图12～14所示.

图12 ITSG机构发布的2009年5月1号几何轨道与JPL发布的约化动力学轨道残差

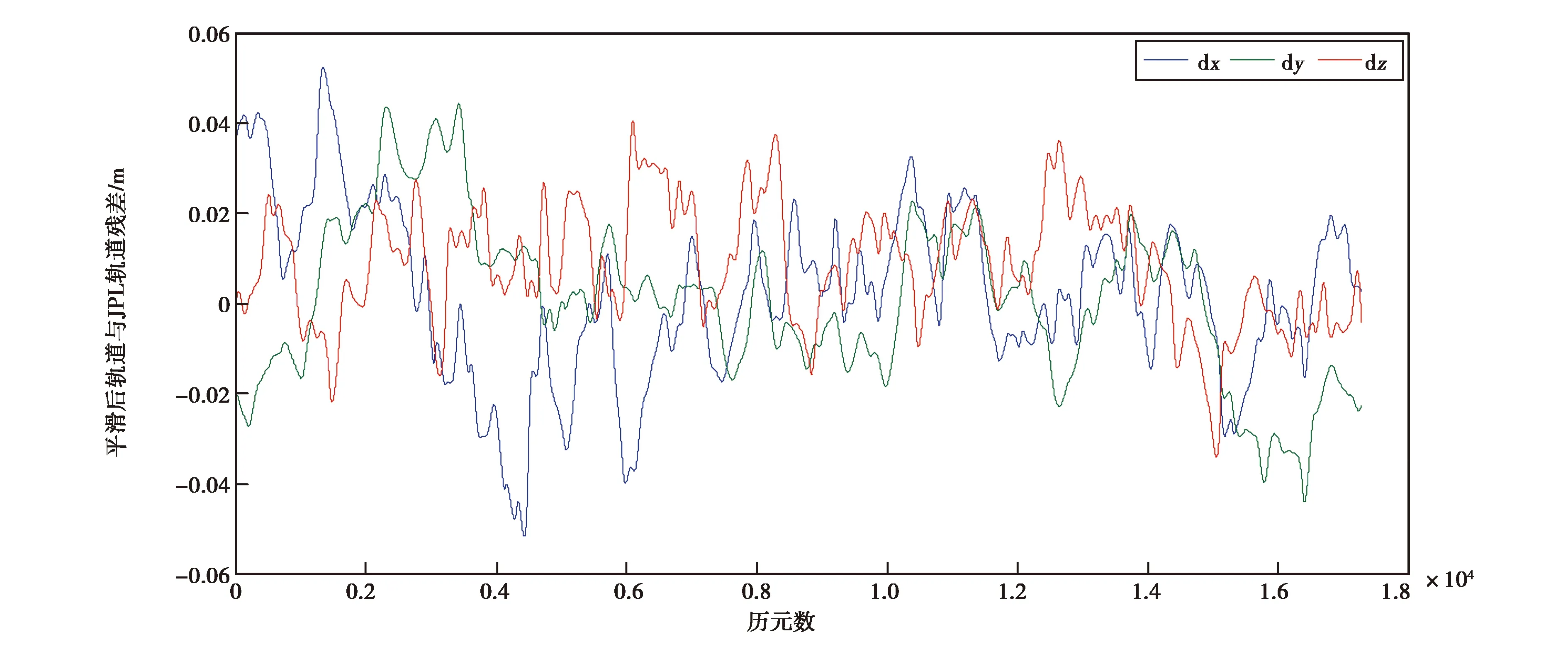
图13 估计策略下积分轨道与JPL发布的2009年5月1号的约化动力学轨道的残差

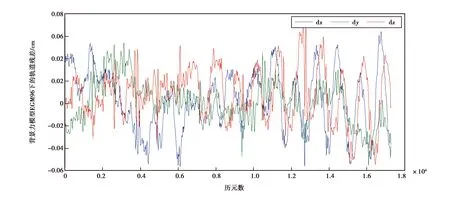
图14 背景力模型为EGM96下的积分轨道与JPL发布的2009年5月1号的约化动力学轨道的残差

表4 GRACE卫星轨道RMS值

由图12～14可知,原始的几何轨道含有明显的偶然误差或者粗差,平滑后的轨道比ITSG的几何轨道更加平滑且数据是没有间断的．由表4可知,平滑后的轨道与JPL约化动力学轨道残差的均方根误差在X方向、Y方向和Z方向相较于ITSG几何轨道均有减小,也证明了实验数据的结论,即在对GRACE几何进行平滑的过程中可通过设置加速计尺度参数和偏差参数来提高轨道的精度．图14为背景重力场模型改为EGM96并采用相同估计策略得到的轨道,当改变背景重力场模型为EGM96时,得到的卫星轨道残差变大,这是由于EGM96重力场模型与GGM05S重力场模型精度差异造成的,先验重力场模型对积分轨道影响明显,只估计尺度和偏差无法有效吸收先验重力场模型的不足．

4 结 论

在利用动力学法实现GRACE卫星轨道平滑的过程中,验证了偏差参数估计时间、偏差估计模型及尺度模型对卫星轨道平滑的影响．基于对比分析得出以下结论:

1) 当采用偏差参数估计时间为15 min、尺度模型为对角填充、偏差模型为1阶的估计策略对GRACE卫星几何轨道进行平滑时,得到平滑后的轨道与JPL发布的约化动力学轨道在三个方向的RMS分别为1.89 cm、1.76 cm、1.56 cm,从整体精度看,解算的GRACE轨道的残差也在cm级．偏差模型的选择和估计时间对平滑后的轨道影响较大,通过缩短偏差参数估计时间,选择对角填充的尺度模型的估计策略,可有效削弱几何轨道的偶然误差,提高轨道精度．

2) 当偏差估计时间增加时,通过选择高阶的偏差模型,也可提高GRACE几何轨道平滑的精度．对于估计时间和参数模型两种条件的影响,估计时间对于轨道平滑的结果影响较为显著．

3) 对于尺度模型的设置可知,其对轨道的影响小于偏差参数及估计时间对轨道的影响,估计时间较长时应采用全填充的尺度模型,估计时间较短可采用对角填充的尺度模型或不考虑尺度参数对轨道的影响．