师徒结对教研形式下，优化初中数学课堂教学的实践与思考

陈晨 周方园

本学期伊始，为促使教师提升教学能力，我校推出了师徒结对制教学形式。其中一项重要的举措是：结对教师每周至少要有一节同课异构。先由徒弟上一节常态课，再由师父给予点评和指导，师徒共同研讨后，由师父上一节示范课，最后设计合适的检测卷，对两个班级学生进行同步测试，从而对比教学效果。

笔者有幸担任了一位刚工作不久周老师的师父。周老师的授课内容是苏科版数学七年级上册“有理数的加减法混合运算”，课后笔者和周老师进行了详细和深入的交流，并整理成文。

一、教学实录和课后研讨

1.复习引入。

（1）教学实录。

周老师（下面简称周）：同学们，上节课我们一起学习了有理数的减法法则：减去一个数，等于加上这个数的相反数。下面，我请四名同学到黑板前做四道练习题：①（-14）-（+16）;②15-（-15）;③（-7）-（-10）;④0-（-13）。

学生板演。

（2）课后研讨。

师父（下面简称师）：周老师，你是如何设计这部分教学的？

周：因为上节课我们学习的是减法法则，而本节课是加减法混合运算，需要将运算中的减法统一改为加法，所以在课堂的开始阶段，我进行了减法运算的专题复习。

师：复习时引入的课堂设计是可以的，但是学生的练习是否应该更多样一些？我建议设计这样一组练习：（1）（-14）-（+16）;（2）（- [34]）+（-20.125）

+[18]+0.75。这样设计既可以考虑到练习的多样性和梯度性，又能让学生复习前面学习的减法法则和加法运算律。因为在加减法混合运算的法则中，除了要将减法转化成加法外，还要注意加法运算律的应用，所以很有必要一起复习。

2.问题探究。

（1）教学实录。

周：请同学们思考，怎样计算（-8）-（+12）+（-3）-（-9）？请同学们先在练习本上独自完成，然后与其他同学讨论交流。

（学生全都独立完成，但是几乎不交流。）

周：（板书正确结果）答案和老师一样的同学请举手。

（一些学生举手，另一些学生则在低头订正。）

周：请同学们思考一下，加减法混合运算中，它的运算步骤是怎样的？同学们可以互相交流一下。

（少部分学生交流。教师参与学生讨论，极力引导学生。）

周：这位同学说说看。

生：减法转化成加法。

周：说的不错，还有吗？

生：想不起来了。

周：老师帮同学们总结一下有理数加减法混合运算的解题步骤：①减法转化为加法;②运用加法运算律;③按有理数加法法则计算。

（2）课后研讨。

师：周老师，你是如何设计这部分教学的？

周：我给出了一个较为简单的有理数加减法混合运算的题目，引导学生去思考并总结出加减法混合运算的步骤。

师：你在复习引入时，只涉及减法法则，大部分学生能通过尝试知道将加减混合运算统一成加法计算。但是，你知道为什么学生在总结加减法混合运算的步骤时，总结得不够全面吗？

周：不知道。

师：因为你在复习引入和问题探究中的例子过于单一，不具有代表性，学生想不到要运用加法运算律。我建议可以这样设计问题：同学们，如果老师把刚才的复习题（- [34]）+（-20.125）

+[18]+0.75，变成（- [34]）-（+20.125）+[18]-（-0.75），你们又将如何解答呢？我相信，学生会饶有兴趣地思考，并知道先将减法转化成加法，然后运用加法运算律，最后利用加法法则得到答案。这样学生就能很快总结出加减混合运算的解题步骤了。

3.例题讲解。

（1）教学实录。

周：下面请同学们继续思考一组例题，并观察老师的解题步骤。

①14-25+12-17;

②（-0.8）+1.2+（-0.7）-（+2.1）-（-0.8）;

③（- [34]）+（-20.125）-6.5+[18]-（0.75）;

周：同学们，只要我们能严格按照刚才总结的三个步骤，就能很好地解决有理数加减法混合运算的习题。

（学生认真看老师的板书。）

（2）课后研讨。

师：周老师，你是如何设计这部分教学的？

周：我想通过一组例题的示范，加深学生对解题步骤的记忆，并能规范书写。

师：你的初衷是好的，但是陷入了应试教育的圈子。主要问题有：此处例题②与之前问题探究中的第①个问题重复;整个过程学生参与度不高，教师反而成为引导学生死记运算步骤的“刽子手”。

師：我建议这样设计习题。

①14-25+12-17;

②（- [34]）+（-20.125）-6.5+[18]-（0.75）。

师：教师到学生身边进行针对性指导，然后请三名完成较为出色的学生到黑板前完成，并依次讲解解题的过程，让学生担任小老师。

4.小结思考。

（1）教学实录。

周：请同学们谈谈这节课的收获。

（学生回答。）

（2）课后研讨。

师：周老师，你觉得如何谈收获？

周：一谈知识收获，二谈其他收获。

师：你所谓的其他收获是什么？学生能回答出来吗？

周：比如小组合作的重要性、数学源于生活等。

师：你说的对，但问题是学生不一定能体会到。此处建议这样设计：①请学生谈收获，②请学生谈还有什么疑问。

二、课堂教学效果对比

笔者在查阅相关文献的基础上，初步设计了“有理数的加减法混合运算”知识问卷，并邀请数学教研组全体教师对问卷内容进行逐一评价，结合教学实际和问卷专业评价标准，如内部一致性系数、内容效度指数等，提出修改意见。

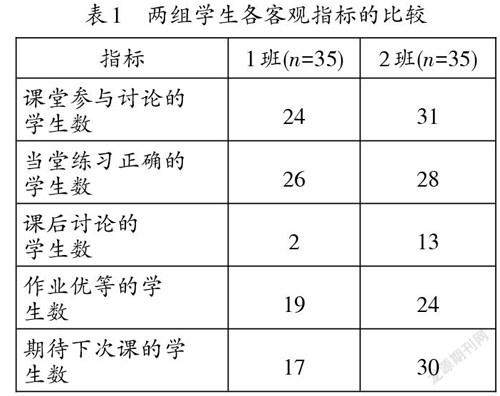
接着，笔者随机抽取本校七年级学生70名，分成两个班，每班35名学生。其中，1班由周老师任教，2班由笔者任教。两班学生在性别、课前测试成绩等方面均无统计学差异。笔者邀请数学教研组教师全程参与两节课课堂教学，记录学生各项客观指标，并在课后将问卷发放给学生填写。

通过分析数学教研组教师的记录数据（如表1），可以很直观地看出，經教研讨论、修改后的教学设计，学生的参与度更高，知识获得率更好，且学习的兴趣更浓。

对于学生问卷调查的结果，笔者利用统计软件，采用统计学方法进行分析。首先对比两班的概念题、基础练习、提高练习的总分和均分，然后对比两班学生问卷总得分和及格情况（总分30分，得分小于18分为不及格），结果显示，笔者重新设计的教学效果明显优于周老师的教学。但对于有理数加减法的提升练习，学生均分差异不是很显著，这说明还需长期训练，教师要多为学生提供提高和展示的舞台。

三、教学反思

在师徒教研的形式下，本节课不是“浓妆艳抹”的公开课，而是更趋于真实的常态课。正因为它的不完美，才造就了它美丽的一面。对于本节课课后教研，还有一些细节值得讨论和分析。

1.怎样培养学生的数学思维？

这是一个始终困扰教师的问题。对于刚工作不久的青年教师来说，他们想让学生从自己课堂上学习到更多的知识。但教师应该怎样设计教学，才能既让学生感受到课堂的妙趣横生，又能收获满满呢？笔者在周老师这节课的教学设计的基础上，做了一些调整：（1）在复习引入和问题探究环节设计了问题串式的提问;（2）例题讲解环节请学生担任小老师做示范;（3）课堂练习环节请学生互相命题和解答;（4）实际应用环节引入数学游戏。

这里每一个设计环节都可以有效地提高课堂的趣味性，通过设计这些数学活动，最终达到培养数学思维的目的。课堂上最美丽的声音，一定是学生的声音;课堂最美丽的收获，一定是学生互动生成的;课堂上最美丽的身影，一定是学生占据课堂核心舞台的纵情表演。因此，要培养学生的数学思维，一定要抓住课堂这个主阵地。

2.为什么减法要转化成加法？

这个问题显然已成为初中数学教材中的一种“人文规定”，但作为教师，要学会理解其中的深刻数学思想。正如北京师范大学郜舒竹教授所言：“数学课程中‘人文规定’的内容，具有较强的主观性，其中蕴含着丰富的思想。”笔者思考了这个问题，觉得有两方面的原因：其一，加法的法则和运算律已经很详细，而减去一个数可以看成加上这个数的相反数，因此，如果将减法转化成加法，既可以减少运算符号的数量，也可以达到简便计算的目的;其二，类比这种方法，乘除法混合运算也可以统一成乘法进行运算。这样就更凸显出这节课承上启下的作用。

（作者单位：江苏省太仓市第一中学）

【参考文献】

[1]陈敏.师徒制下数学新教师MPCK发展的个案研究[D].苏州：苏州大学， 2019.

[2]韩新正.推敲“理所当然”  感悟数学严谨[J]. 课程·教材·教法， 2018（9）.

[3]胡梦尧，陈天宇.对有理数四则运算的深度剖析[J]. 数学教学通讯， 2017（5）.