Energy Efficiency Maximization Strategy for Sink Node in SWIPT-Enabled Sensor-Cloud Based on Optimal Stopping Rules

Zhe Wang,Lina Ge,Taoshen Li,Guifen Zhang,Min Wu,4

1 Institute of Artificial Intelligence,Guangxi University for Nationalities,Nanning 530004,China

2 Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis,Nanning 530006,China

3 School of Computer,Electronics and Information,Guangxi University,Nanning 530006,China

4 Guangxi Power Grid Co.,Ltd,Nanning 530023,China

Abstract:Leveraging energy harvesting abilities in wireless network devices has emerged as an effective way to prolong the lifetime of energy constrained systems.The system gains are usually optimized by designing resource allocation algorithm appropriately.However,few works focus on the interaction that channel's time-vary characters make the energy transfer inefficiently.To address this,we propose a novel system operation sequence for sensor-cloud system where the Sinks provide SWIPT for sensor nodes opportunistically during downlink phase and collect the data transmitted from sensor nodes in uplink phase.Then,the energy-efficiency maximization problem of the Sinks is presented by considering the time costs and energy consumption of channel detection.It is proved that the formulated problem is an optimal stopping process with optimal stopping rules.An optimal energy-efficiency(OEE)algorithm is designed to obtain the optimal stopping rules for SWIPT.Finally,the simulations are performed based on the OEE algorithm compared with the other two strategies to verify the effectiveness and gains in improving the system efficiency.

Keywords:sensor-cloud;SWIPT;optimal stopping theory;energy efficiency;channel quality

I.INTRODUCTION

Sensor-cloud system is produced by injecting the cloud computing technology into wireless sensor networks (WSNs).The former expands the WSN's capabilities in data processing and storage.It can deal with the data generated by the underlying sensor network,which makes the system autonomy and gives users remote access.The latter realizes the connection between the information system and the real world,and becomes an important part of the Internet of Things (IoT) and Cyber-Physical Systems (CPS).However,the development of the sensor-cloud system is restricted as its growing scale and quantity lead to greater energy consumption,and the sensors' energy is limited and difficult to recharge at the same time.

Recently,applying energy harvesting (EH) and wireless power transfer(WPT)techniques in networks led to the emergence of energy harvesting network(EHN),in which nodes are equipped with EH devices to extract energy(wind,solar,radio frequency,and so on) from their surroundings.The energy harvested by nodes is converted to DC power to revive themselves for perception and communication [1-4].The EHN provides two forms of wireless information and power transfer,namely Simultaneous Wireless Information and Power Transfer (SWIPT) and Wirelessly Powered Communication Networks (WPCNs).The former realizes the operation of wireless energy transfer(WET)and wireless information transfer(WIT)using a same radio wave simultaneously,while the latter is operated in different time sequences.Therefore,in order to make a breakthrough in the application of the sensor-cloud system,EHNs are considered to take into account to reduce the traditional energy consumption of the system and prolong nodes'lifetime.

Traditionally,there are two ways to recharge a EH node in WPT-enabled WSN.One is to transfer wireless power to the node through the planned path using a Wireless Charging Vehicle(WCV)carried electromagnetic radiation devices [5-8],the other is to power the node through magnetic resonances [9-12]or beamforming[13-18]wirelessly by a dedicated hybrid access point(H-AP).In[13],to maximize the energy transfer efficiency in wirelessly powered sensor networks,the authors propose a cooperative SWIPT Scheme.Furthermore,this works show that shadings and non-line-of-sight links make the energy power transfer inefficiently,which is unfavorable for WPT applications.Reference [14]studies the beneficial combination of WPT and millimeter-wave(mmWave)communications in WSNs.In particular,an mmWave beamforming scheme is considered,where the AP transfers wireless power to sensor nodes in a selected cell.The performance of the network is discussed based on the energy outage probability during downlink phase and the beam outage probability during uplink phase,respectively.The results show that the performance suffers from both small-scale block fading and large-scale path-loss effects as the mmWave channel is characterized by strong line-of-sight link and weak non-line-of-sight link,separately.In [15],a problem of joint optimal sensor deployment,WET scheduling,and node activation is posed and investigated in wireless powered sensor networks,in which the channel states are modeled as bounded functions to use least number of chargers under minimum sample rate constraints.The work in[16]studies the system achievable rate maximization problem in SWIPTenabled cognitive WSNs.the authors jointly optimize the transmit power and power split (PS) radio under tolerable interferences.In particular,the channel coefficients are affected by end-user's distance,path loss index and Rayleigh fading coefficients.Different from[16],[17]analyzes the channel performance based on Nakagami-m fading model in SWIPT WSNs.In detail,the probability density function and cumulative distribution function of the signal-to-interferenceplus-noise-ratio in high signal-to-noise ratio region are characterized firstly,and then the authors study the outage and ergodic capacity performance of the backward links through Monte Carlo simulations.The WSNs with MIMO SWIPT are further studied in[18],where base station transmits the energy signal to sensors at first phase,and schedules sensors intelligently to reduce interference based on beam-domain distributions of channels at second phase.Finally,the receive beamformers are formed by base station according to the reception of signals transmitted by sensors.In particular,the downlink in first phase and the uplink in second phase are both modeled as general cluster channels[19].

In WPT-enabled WSNs,the gains of the system are not only related to the operation decisions,but also the channel states.The decisions made by above works are not able to deal with the time-very nature of the channel states even which is well described by different channel models.Meanwhile,the power and information are transmitting at all times,when the channel state is not good,the transmit power has to be increased to meet the node's energy harvesting demands,which leads to a waste of system resources.On the other hand,due to the Double near-far [3,4,20]appearances,channel state affects both the energy transfer of the downlink and the information transmit of the uplink,the efficiency of energy will be greatly improved if the best channel state is selected dynamically to transmit the power and information.Therefore,in the WPT-enabled WSNs,the time-varying characteristics of channels should be taking into account;system decisions should choose the good channel states to obtain higher energy utilization.

To overcome the fluctuation of wireless fading channels,opportunity scheduling schemes are proposed to dynamically allocate resources to the best Instant Wireless channel,which are divided into Centralized Opportunistic Scheduling (COS) and Distributed Opportunistic Scheduling (DOS).The former estimates the channel and makes system decisions centrally in the base station,while the latter are separately optimized in an uncooperative way [20].Reference [21]firstly proposes two DOS schemes for Ad-hoc with random access channels.The one maximizes the total throughput by user cooperation,another maximum each user's throughput without cooperation.Furthermore,[22]adds average delay constraints for problem formulation,maximum the throughputs based on the two schemes proposed in [21].Similarly,[23]develops a DOS two-level detection method to solve the channel estimation problem in [21],the result shows that the two-level detection method is improved by 110% system gains.Reference [24]pointed out a shortcoming of DOS in [21],[22]and [23],that is,the DOS schemes are formulated only considering the situation of user totally saturated,such as the user's transmission queue is completely backlogged.However,in practice,the queues of different users are not the same,it is necessary to consider the case where the user may not have enough data for transmission when participating in channel competitions,which is called the no user transmission intervals.Afterwards,an adaptive DOS(ADOS)strategy is proposed by optimizing the transmission rate threshold and access probability to overcome the shortcoming.The results show that the ADOS strategy increases the energy efficiency with respect to DOS up to 30%for proportional fairness cases.However,those strategies in above works are not applicable for WPT-enabled networks as they are meanly designed for information networks.Meanwhile,due to the limitation of energy,an appropriate time should be well selected for energy transfer to reduce the path loss of energy in wireless channels,and improve system efficiency.

Generally,the channel state in a wireless network is varying with time,which determines the energy utilization in the channel use.That is to say,when the energy is always transmitted at the best of the channel state,the energy utility efficiency of WPT-enabled network will be the best.Inspired by the opportunity scheduling,this paper proposes an optimal energy efficiency strategy for SWIPT in downlink of WPTenabled sensor-cloud networks based on optimal stopping theory.A central goal of this strategy is to find the optimal time for Sink nodes to begin SWIPT and maximizes energy efficiency while considering the channel's time-varying characteristics.This is in contrast to traditional optimization approaches for sensor nodes diversities based on instantaneous CSI,and is also in contrast to the recent work[25]that proposes a clusterbased opportunistic scheduling policy to group energy receivers (ERs) into clusters for WET based on Received Signal Strength Indicator (RSSI).In [25],a channel estimation method is designed to realize the ERs diversities to determine which nodes or clusters are allowed to receive wireless energy.However,the transmitter is still working all the time for WET even the selected cluster does not have a good enough but is the best RSSI at present.This problem will be well studied in this paper by optimal stopping rules to find the best time to begin SWIPT in an activated cell.The main contributions of this paper are summarized as follows.

(1) System operation sequence design.For WPTenabled WSN in sensor-cloud,we first design a downlink SWIPT and uplink information transmit time sequence,in which the base station chooses the best time to begin SWIPT for cloud assignment dispatching during down phase,and collects the data generated by sensors during up phase.All the energy for sensors operation is harvested from SWIPT signals transmitted by the Sink nodes.

(2)Optimal energy-efficiency problem formulation.Due to the different channel state in different intervals,the downlink SWIPT allows the Sink detects the channel dynamically for many times and chooses the best intervals for SWIPT.This process can be formulated as an optimal energy-efficiency problem by considering the time costs and energy consumption of channel detections.The problem is an equilibrium problem with optimal stopping rules.

(3) Optimal energy-efficiency algorithm.Based on the optimal stopping theory,optimal energy-efficiency algorithm is designed to obtain the optimal stopping rules for SWIPT,that is,the best time for downlink SWIPT begins.The optimal energy-efficiency algorithm is compared with two different transmission scheduling strategies.

The rest of this paper is organized as follows.The system model is introduced in Section II based on the design of system operation sequence.Section III formulates the optimal energy-efficiency problem and proves the optimal stopping rules exits.In Section IV,an optimal energy-efficiency algorithm is designed to solve the problem and find the best approaches.Finally,simulations and analysis are given in Section V,followed by the conclusions in Section VI.

II.SYSTEM MODEL AND OPERATION SEQUENCE

The framework of sensor-cloud system is shown in Figure 1,where the sensor nodes are uniformly distributed in the underlying as a cellular network composed of many hexagonal cells.The Sink nodes are supposed to be in the central of each cell and powered by stable supplies.The sensor nodes are harvesting energy and decoding information simultaneously from the RF signals transmitted by Sink nodes based on power splitting (PS) mechanism.Limited by the size and cost of wireless devices,both the Sink nodes and sensor nodes are equipped with single antenna.This configuration does not make a difference on the fairness of the optimization goals and the single scenes can be expand to antenna arrays by converting channel coefficients into channel vectors.

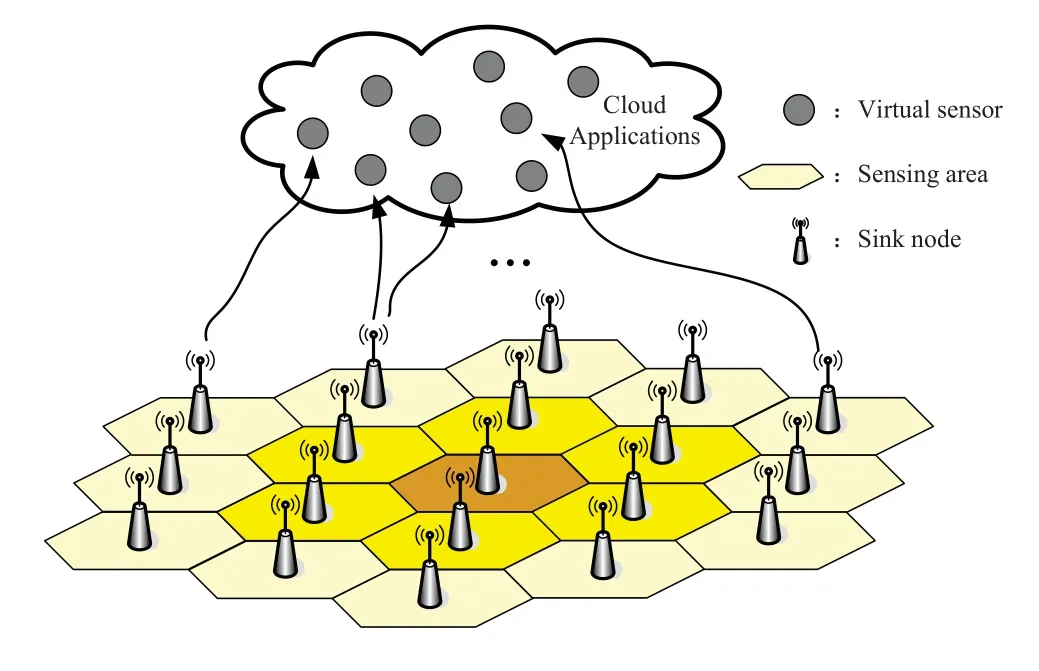
Figure1.Sensor-cloud system.

In the underlying network,the Sink node in a central cell can detect the communicating status of other Sink nodes in the neighbor cells.That is to say,the central Sink node and its six neighbor Sink nodes are competing to access the downlink channel randomly,only one Sink node in a time slot can be allowed to provide SWIPT for sensor nodes in the same cell after a successful competition.Specially,the Sink node can obtain the channel-state information (CSI) to the channel,which may be good or bad during to the time-varying characteristics of channel fading.The goal in this paper is to find the good channel to begin downlink SWIPT to maximum resource utilization of sensor-cloud.

2.1 Operation Sequence

Assumed that the channel states of neighbor links can be obtained by the Sink node through sharing information in the upper cloud.The Sink nodes in the interference range access randomly channel and the successful Sink node obtains the CSI.If the information and power are transmitting in a channel with bad CSI,the Sink node have to increase its transmitting power to meets the sensor nodes' energy harvesting needs.Even worse,the appearance of Double near-far in WPT-enabled networks makes the remote sensors needs more energy than the closers.All these disadvantages lead to an inefficient and high consumptive SWIPT for sensor-clouds.A reasonable approach is to plan the Sink node to choose a better channel to start SWIPT with good CSI.

Based on the above descriptions,we design the sensor-cloud operation sequence,as shown in Figure2.Suppose the system performsYtasks,each task's process contains three steps.First,the Sink node participates in channel competitions until successful access the channel.Second,the Sink node decides whether to start downlink SWIPT by broadcasting in current channel use based on the CSI.If the CSI is good (which will be evaluated based on optimal stopping rules in the Section IV),SWIPT is started immediately in the current slot,otherwise,the Sink node gives up this channel use and waiting for the next competition.Third,the sensor nodes upload collected data to the Sink node using the energy harvested during the previous downlink SWIPT time slot.In the sensor cloud system,it is assumed that the period of WPCN composed of Sink nodes and sensor nodes isT,in which the downlink duration istand the channel detection time isτ.In the wireless link composed of Sink node and sensor node,the channel gaingobeys a certain distribution(such as Rayleigh distribution [26]).It is assumed that the channel detection period is greater than the coherent time length of the channel,and the downlink SWIPT time should not be greater than the coherent time length of the channel.Then,we establish the system mathematical models.

2.2 Downlink Phase

Suppose that the central cell and neighbor cells are formed as an interference network.Here,the number of Sink nodes in the interference network isK,K=7.

The once channel competition in the interference network can be described as follows:

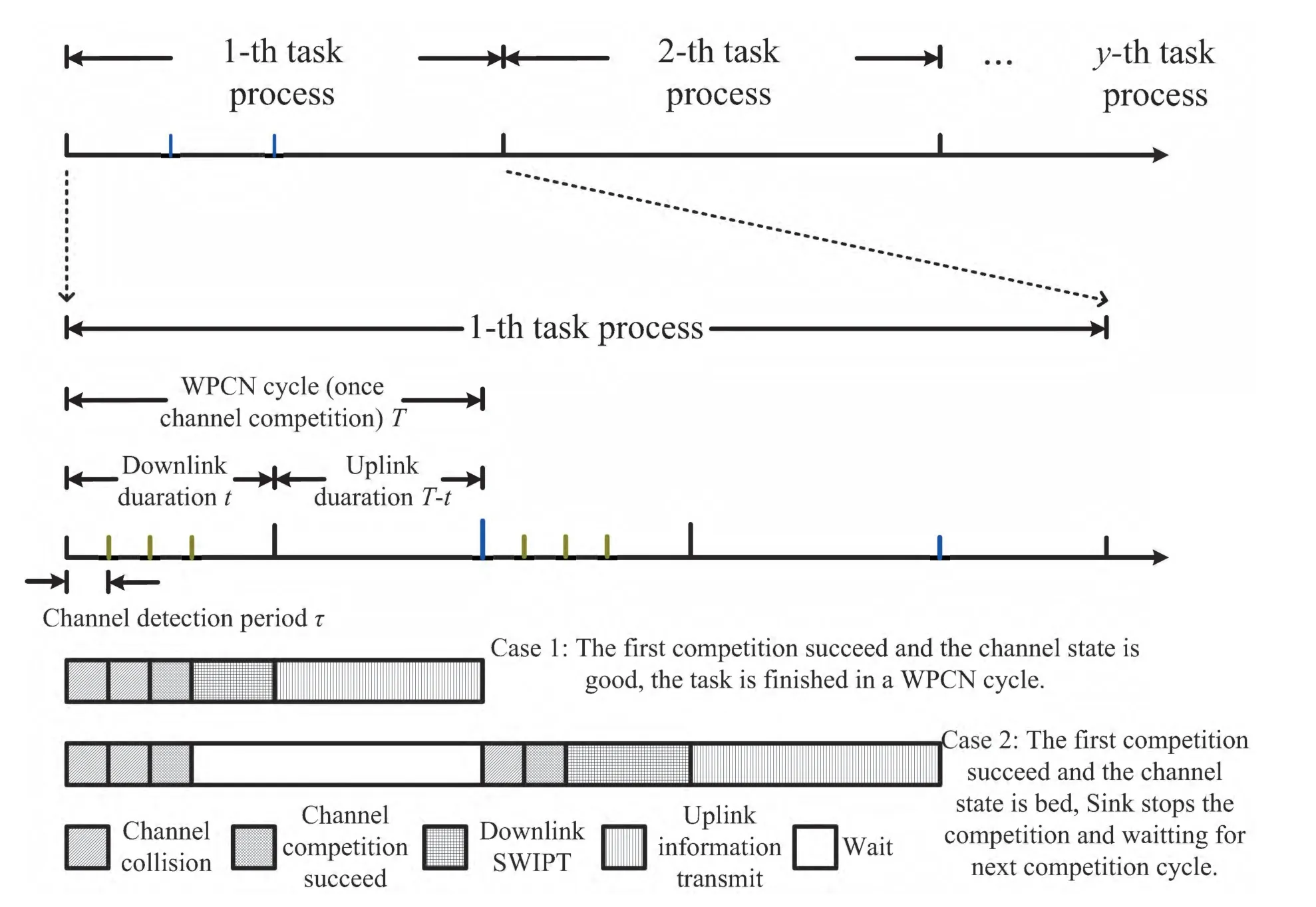
Figure2.System operation sequence.

TheKSink nodes participate in channel competition with equal probabilityp,p=1/K.When only one Sink node is competing channel while the downlink is idle at this moment,it is called that the first-time channel competition successfully.Here the access node is denoted as Sink A.If the channel quantity is good for SWIPT,Sink A transmits the information and power to sensor nodes in its servicing cell simultaneously;otherwise,the Sink A quits from the channel competition and waiting for next competition while theK-1 Sink nodes continue to compete the channel.The second time channel competition is successful when there is only one Sink node access the channel which can be called Sink B.Sink B performs the same operation as Sink A.Sink B begins downlink SWIPT if the CSI is good at this time.Otherwise,Sink B quits while the remainingK-2 Sink nodes continue.

During the downlink phase,the Sink node competed successfully obtains the chance for SWIPT in the rest of the durationt.Therefore,the channel in the interference network is competed successfully forKtimes.

In the current interference network,the probability of channel successfully be competed in thei-th competition can be denoted as

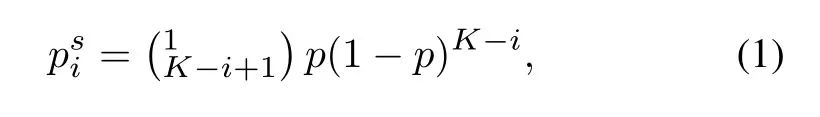
Then,the expected time of competition needed for the channel successfully competed ati-th is obtained,which isni=1/psi.And the expected time of competition for the Sink node accessed the channel isnip.The total expected time of competition for downlinkSuppose the transmit power of the Sink node isP,then the consumption for once channel competition isPτand the total expected consumption for downlink competitions can be expressed asIf the channel quality is good at the moment,downlink SWIPT begins.Therefore,the time consumed until the channel successfully competed at first time and the rest of the time for SWIPT are separately denoted asn1τand(t-n1τ).

In practice,the Sink node cannot wait for SWIPT all the time.We set the maximum delay for SWIPT asD.If a Sink node successfully accesses the channel and the maximum delayDis reached at present,the downlink SWIPT begins immediately without considering the channel quality.Obviously,the total exis pected number of competitions when the Sink node reached the maximum delay isn1p,the corresponding expected consumption,expected consumed time and rest time for SWIPT arePτn1p,n1τand (t-n1τ),respectively.

According to the Shannon theorem,the better the channel quality is,the more energy the sensor node can harvest and the bigger throughput is realized for the Sink node.Specially,the throughput of uplink is established in the following section.

2.3 Uplink Phase

As a result of downlink durationt,the remaining duration for uplink is (T-t).The sensor nodes transmit data simultaneously to the Sink node using the energy harvested during the previous downlink SWIPT duration and the transmitted signals will be detected by Sink node with Maximal Ratio Combining(MRC)algorithm [26].Suppose the number of sensor nodes in the cell isM,then the energy harvested ofm-th sensor node during the downlink SWIPT phase can be denoted asηmαmPtS,in which theηm,αmandtSseparately represent the path loss factor,power splitting ratio and downlink SWIPT duration.Based on Shannon formula,the rate achieved by the sensor nodemduring uplink phase can be written as

where theRmis channel capacity,gmis the channel gain,Wmis the bandwidth,Psmis the transmit power of sensorm,N0is the spectrum density of noise.Then,the throughput of sensor nodemin the cell during uplink phase is

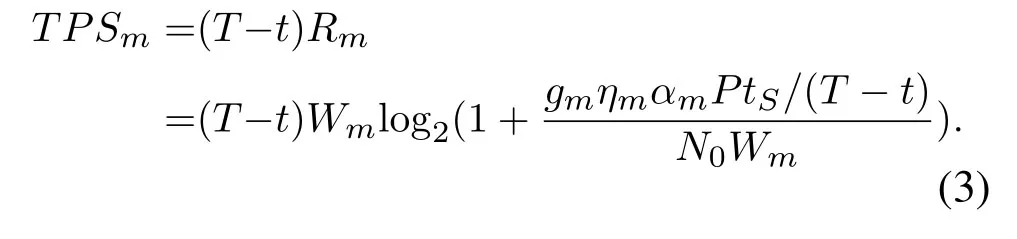
2.4 Sink's Energy-efficiency Model

Assumed that the amount of information transmitted by the Sink node in the downlink phase is far less than the energy,that is to say,the information for the task can be transmitted completely during the downlink duration.The power split ratio of sensor node for harvesting is preseted as a fixed value,thus the task information can be fully received and decoded in the downlink phase.Then,the energy harvested by the sensor node depends on the Sink transmit power and the CSI.According to the law of energy conservation,the energy consumed by a sensor node for sensing and information processing is a part of the SWIPT energy transferred by the Sink node.We assumed that the transmit power of sensor node for uploading is equal to the ratio of node's energy harvested to the uplink duration,that is,the sensor node completely uses the energy harvested in the downlink phase for uplink data transmission.Then,the process of a task successfully performed can be defined as a continuous procedure from the Sink node accesses the channel for downlink SWIPT to the sensor nodes upload their data to the Sink node completely.A task process containsNchannel competitions.Due to the maximum delayD,theNbelongs to the set{1,2,...,ND},whereND=D/T」.Hence,we define the system energyefficiency as the total throughput of uplinks achieved by all sensor nodes divided by the total energy consumption of Sink node for the task in the current cell,which is

In (4),the numerator is the sum of sensor node's throughput for uploading their collected data,the denominator is the total energy consumption of the Sink node.Specially,the energy consumed for SWIPT isPts,wherets=t-n1τ.TheEis the total consumption of the Sink node before accesses the channel successfully,which can be denoted as

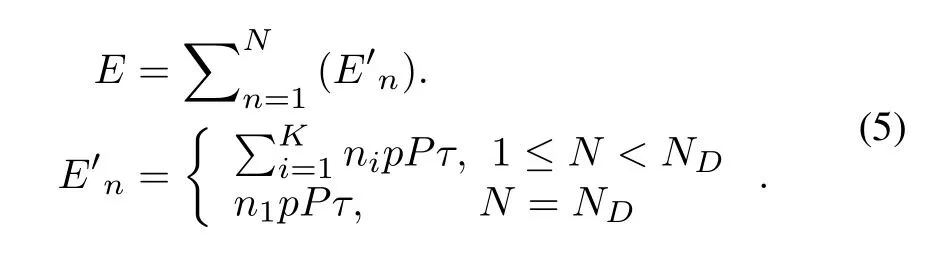
Generally,the average energy-efficiency ofYtasks is given as:

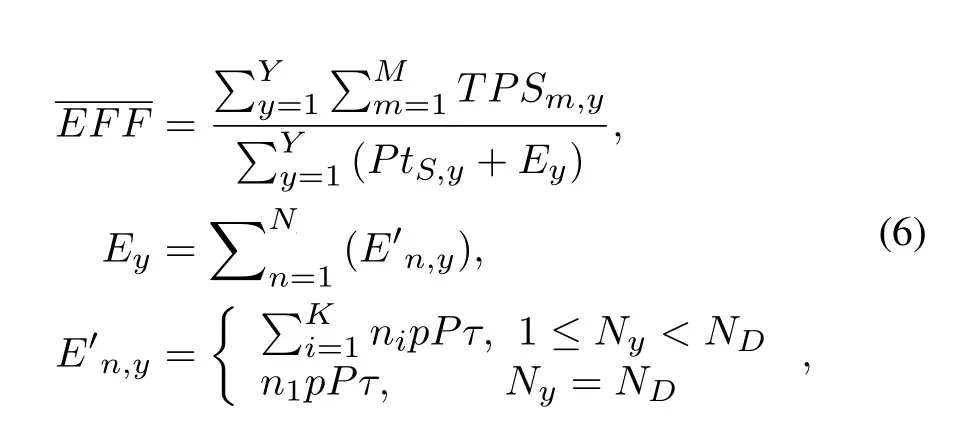
whereTPSm,y,tS,yandNyare the uplink throughput achieved bym-th sensor node,the downlink SWIPT duration and the number of channel competitions iny-th task.

III.PROBLEM FORMULATION

According to the average energy-efficiency,we formulate the optimal energy-efficiency problem in this section,and prove the optimal stop rules are existed.

Based on the Law of Large Numbers,equation (6)approaches to

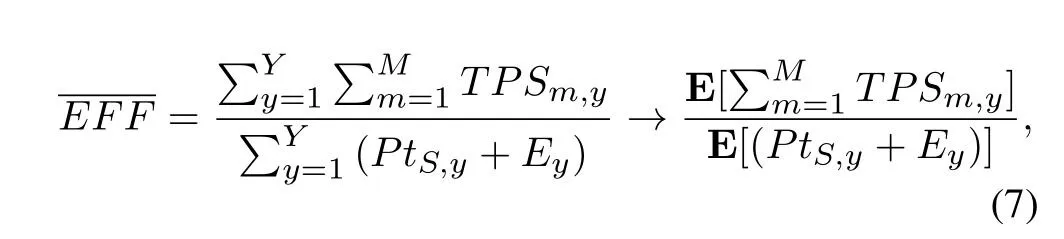
in which the E[·]is the mathematical expectation function.Define the set N={1,2,...,ND},then the average energy-efficiency maximum problem is formulated as

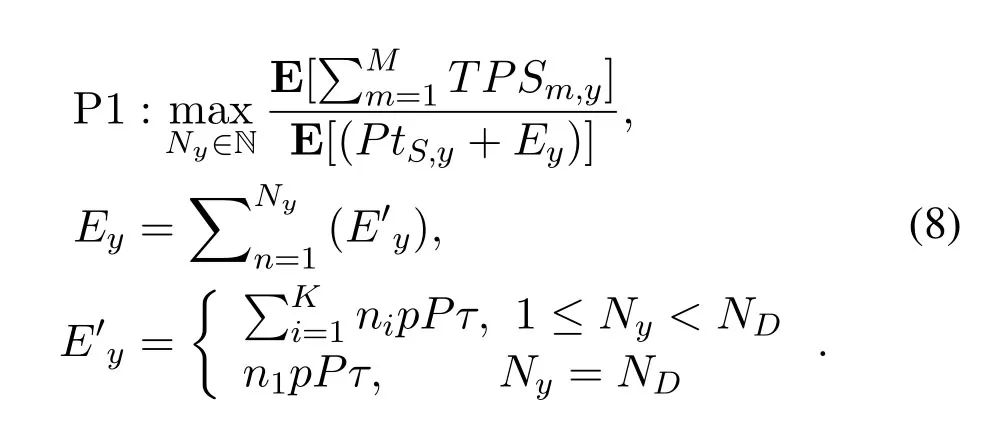
Then,the optimal average energy-efficiency of the system afterYtasks is obtained by combining (7)and(8),which is written as

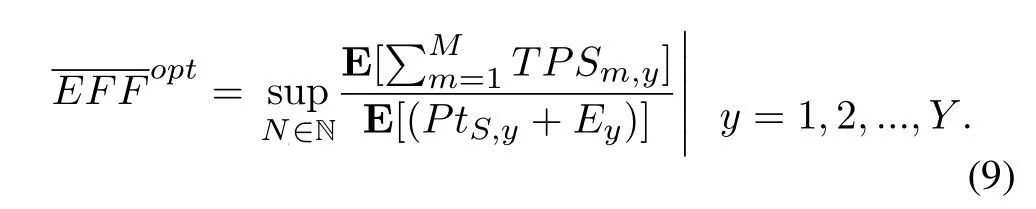
After equivalence transformation,the (9) can be rewritten as

The(10)is an optimization problem for the expectation reward Emaximum with respect toin which the reward function denoted byis

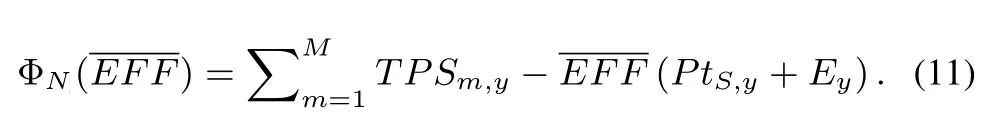
Consequently,the optimal stopping problem can be produced from(8)as:

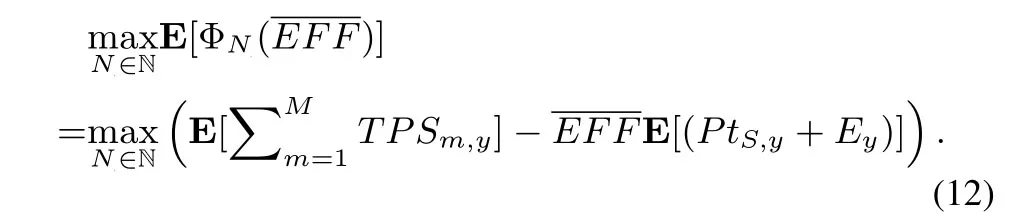
The goal of (12) is to find the optimal average energy-efficiencywith the optimal stop timeof channel competition.Here,the system maximum expectation reward isand the corresponding optimal stop timeis written as

Next,the average energy-efficiency maximum problem in(12)is proved to be a limited optimal stopping problem with optimal stopping rule exists.

Theorem 1.There is an optimal stopping rule to the maximum problem of average energy-efficiency in(12).

Theorem 1 is proved in Appendix A.

IV.OPTIMAL STOPPING RULE

The Sink node participates in the channel competition at the beginning of each task.After successfully accesses the channel,Sink decides whether to transfer wireless power and information to sensor nodes in current duration according to the detected CSI.In practice,the decision is made by the comparison of expectation reward for current and for future.If the Sink node obtains the channel use after Ny channel competitions,then the reward for it stop competing and begin downlink SWIPT is

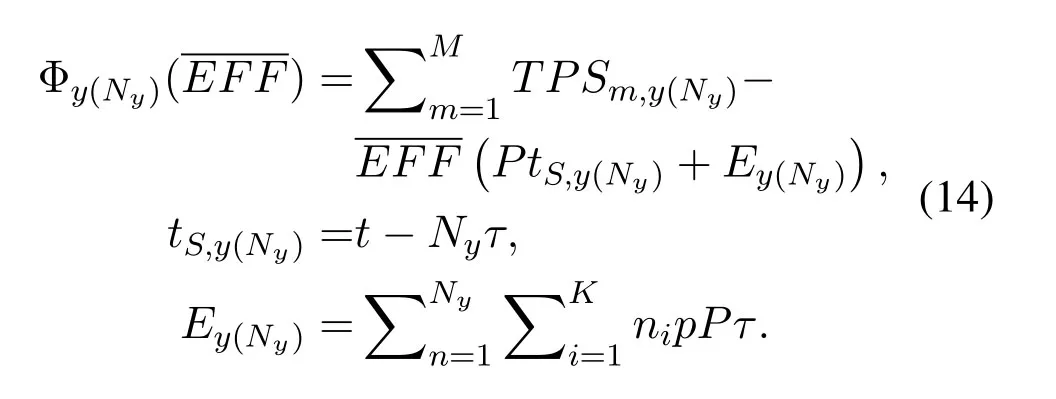
where,y(Ny)is defined as the Sink node successfully accesses the channel afterNychannel competitions iny-th task while the SWIPT begins subsequently.If the Sink node gives up the chance for SWIPT this time,the expectation reward obtained is

In (15),Fy(Ny)denotes the uplink throughput sequencethe duration sequencetS,1(N1),...,tS,y(Ny)for SWIPT and the total consumption sequenceE1(N1),...,Ey(Ny)for competitions separately obtained byytasks.Based on the candidate optimal stopping rules [27],if the expected rewardfor SWIPT while the Sink node accesses the channel successfully afterNycompetitions iny-th task is not less than the expectation rewardthe Sink node should begin to provide downlink SWIPT to sensor nodes immediately.Otherwise,the Sink node waiting for the next competition.Therefore,the condition for SWIPT begins afterNycompetitions,is

Theorem 2.Ifas well as the stopping rule satisfies thethesopping rule is optimal.Where,

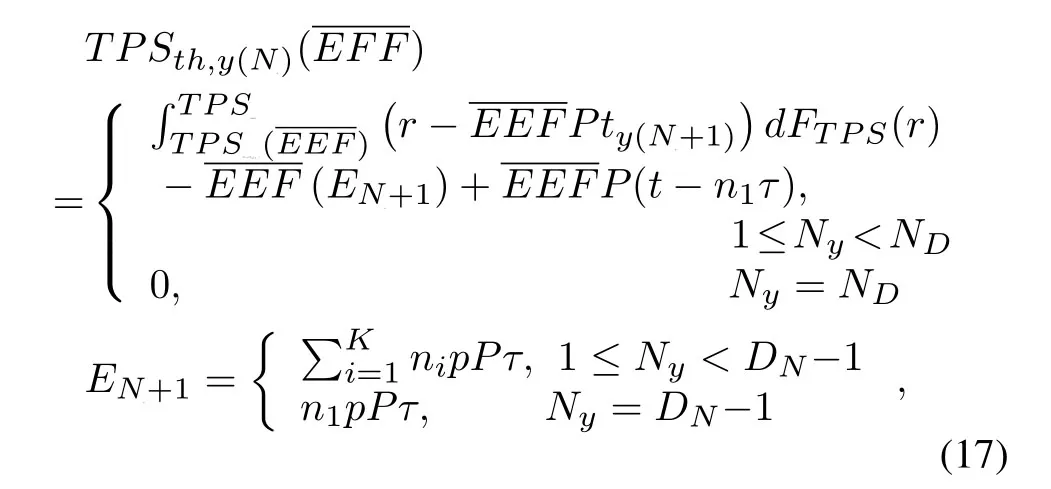
the FTPS(r)is the cumulative distribution function(CDF)of uplink throughput.

Theorem 2 is proved in Appendix B.

Depending on Theorem 2,the optimal stopping rule of(12)can be written as

Finally,the optimal average energy-efficiencyis obtained by substituting(18)into(9).

Assume that the channel gaingmhas the CDFF(gm),and the CDF of uplink throughput isFTPS(r).Due to the probability for Sink node access the channel of in each channel competition isp=1/K,the probability of first time for the Sink node successfully competition and SWIPT begins can be calculated,which isand the probability of Sink node quits isTherefore,the probability for Sink node access the channel after competitions and begin SWIPT is

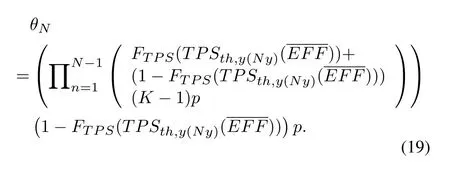
At this point,the expected duration for downlink SWIPT and the expected uplink throughput are

respectively.Afterytasks,the system total throughput,downlink SWIPT expected energy consumption and expected competition consumption are

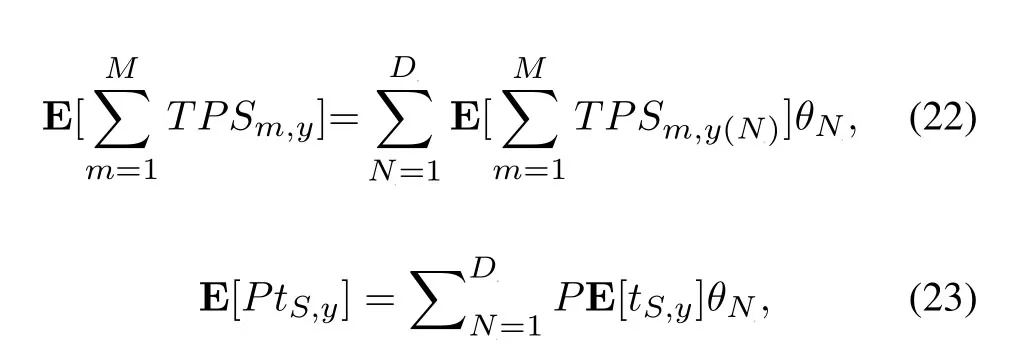
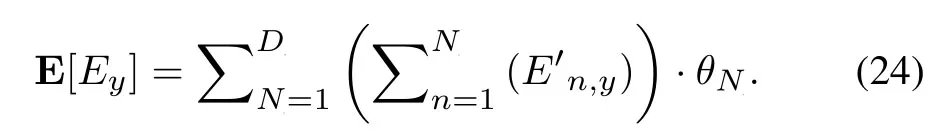
After substituting(22),(23)and(24)into(9),the optimal average energy-efficiencyis obtained.We design an optimal energy-efficiency (OEE) algorithm 1 to find the optimal average energy-efficiencyAfter initialized theis chosen by Newton iterative method.

?

Algorithm 1 quadratic convergences to the optimal solution.At least,the optimal average energyefficiencyis substituted into optimal stopping rule(17),then the Sink node obtains the uplink throughput threshold of downlink SWIPT after Ny-th successfully competed channel,which contributes to the optimal downlink starting time.

V.SIMULATION AND DISCUSSION

In this section,simulations are carried out for the proposed optimal energy efficiency downlink SWIPT strategy.It is assumed that the sensor nodes in the cell immediately start the uplink data transmission at the beginning of the uplink phase,and the transmission power is equal to the ratio of the energy harvested in the downlink phase to the duration of the uplink phase.The fluctuation characteristics of the wireless channel obey a known long-term statistical distribution function,and the probability density function of the channel can be directly estimated by the nonparametric density estimation method based on the measured data [28].At the same time,it is assumed that the transmitter can sense the instantaneous CSI of the channel based on the channel estimation method of pilot or training [29].Therefore,the minimum time intervalτbetween two competing channels of a link is greater than the coherent time of the channel,and the channel state remains stable in the coherent time[29,30],Therefore,the number of computationsKfor a channel successful accessed is a geometric random variable.Assuming that the transmit power of Sink is a certain value during the downlink SWIPT,that is,the channel state is invariant during the process,and the transmission time of SWIPT should be less than or equal to the channel coherent time.Considering that the channel fading obeys Rayleigh distribution [31],Rician distribution[31]and Nakagami-m distribution[32]respectively.Then the effectiveness of the proposed OEE algorithm for the three fading channels is verified.Finally,the optimal energy efficiency strategy is compared with the other two strategies to prove the system gains realized by the proposed method.The parameters for simulation are shown in Table1.

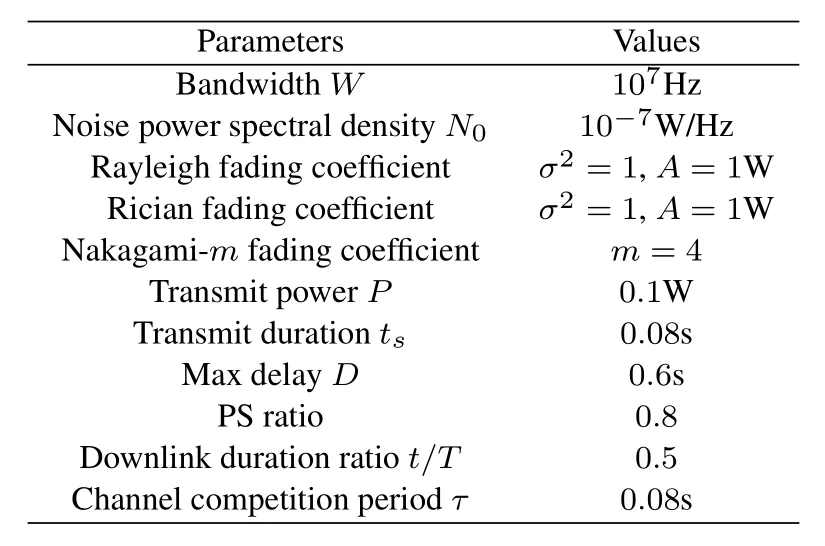
Table1.Parameters for simulation.

5.1 Simulation Of Algorithm

First,30 tasks are carried out to obtain the optimal stop time by Algorithm 1.In practice,theis initialized as bit/Hz/J.Different maximum delays are set to verify the effectiveness of Algorithm 1.The optimal stopping rules for Sink node starts SWIPT are shown in Figure3.For different delays,the optimal stopping rules realized under the three channel models are significantly different,which are distributed between the minimum 1 and maximumND.It is worth noting that the optimal time for SWIPT is more likely distributed close to the maximum delay.This is because the optimal stopping rule made in current period is based on the average energy-efficiency sequence which is achieved in the previous periods,that is,the sensorcloud system tends to the future periods to have better expected system performance.On the other hand,a longer downlink SWIPT duration can increase the system's degree of freedom,which means that in the case of a longer competing duration,the number of tasks with the maximum delay reached for the downlink SWIPT is far less than the number of tasks with the maximum delay reached in the case of a shorter competition period.

5.2 Simulations Of Optimal Energy-Efficiency Downlink SWIPT

In this section,the optimal energy-efficiency strategy proposed in this paper is compared with the other two strategies to verify the effectiveness and gains in improving the efficiency of energy.The strategies participated in the comparative simulations are as follows:

Second,different transmit power of the Sink node are set up to get the optimal stopping rules by Algorithm 1 for 50 calculations under three different channel models,as shown in Figure4.Among them,the optimal stopping time under Rayleigh channel is closer to the maximum delayNDthan the rules obtained under other two channels.Because the other two channels are more coincident with real cases and have less uncertainties,the system needs more time to match the optimal stopping rule that can meet the preset error value.Meanwhile,with the increase of the transmit power of Sink node,the optimal solution calculated by Algorithm 1 is occurred ahead of time.This is because the larger transmit power makes up for the uncertainty of the channel to a certain extent and achieves the compromise for system gains.

Strategy I:Optimal energy-efficiency strategy.The parameters are shown in Table1;

Strategy II:Random downlink strategy.K Sink nodes access the channel randomly.When only one sink node participates in the channel competition,the channel is obtained and the downlink SWIPT starts.Otherwise,the Sink node waits for the next round of channel competition until the maximum delay is reached;

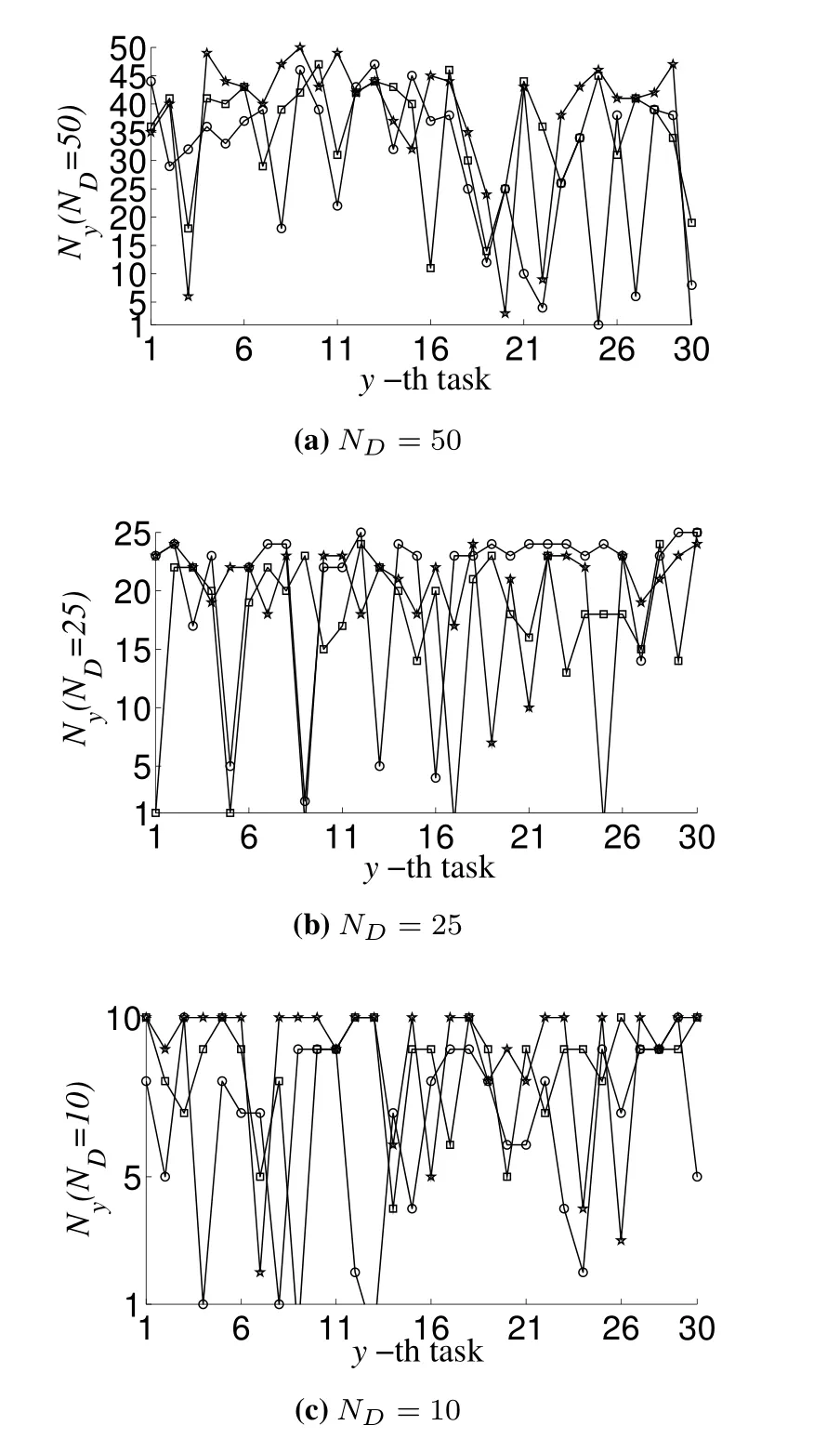
Figure3.Optimal starting time for downlink SWIPT in 30 tasks with different maximum delay ((a)ND=50,(b)ND=25,(c)ND=10).

Strategy III:Distributed opportunistic scheduling strategy in Reference[29].KSink nodes compete for the channel.When only one Sink node competes for the channel and the transmit rate is greater than the threshold,the Sink node starts the downlink SWIPT.Otherwise,the Sink node gives up and waits for the next round of channel competition.The transmission rate refers to the maximum expected transmission rate that can be realized after the channel is obtained.

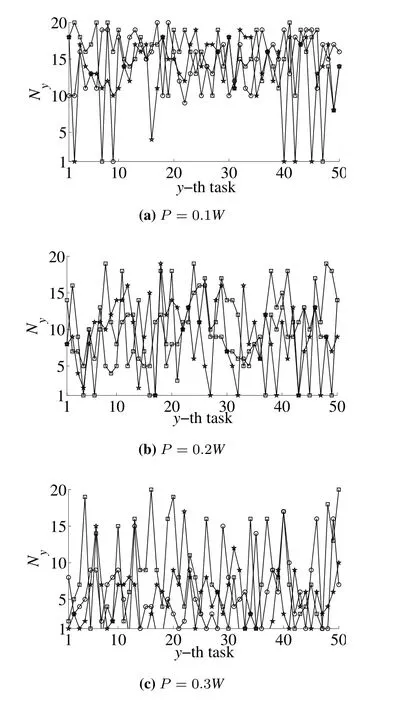
Figure4.Optimal starting time for downlink SWIPT in 50 tasks with different transmit power by the Sink node((a)P=0.1W,(b)P=0.2W,(c)P=0.3W).

The system energy efficiencies of those three strategies are calculated under the Rayleigh fading channel,Rician fading channel and Nakagami-mfading channel,as shown in Figure5.The comparisons of the system energy efficiency realized by three different strategies are made from the aspects of the length of downlink durations,the durations of channel quality retain,transmit power,the number of sensor nodes,the maximum delay and the channel competition period.It is concluded that the optimal energy-efficiency strategy in this paper achieves better system gains than the other two strategies,and the random downlink strategy does not consider the channel Quality,which is followed by the optimal energy-efficiency strategy.In Strategy III,the optimal threshold does not consider the maximum downlink delay and the channel quality remaining,when the downlink fails to reach the optimal threshold,it needs to wait for channel competition all the time,which results in the increase of competitive energy consumption and the worst system performance.Figure5a shows the system energy efficiency realized by different downlink periods.When the downlink duration increases to a certain extent,the system energy efficiency declines.This is because that although the longer downlink period leads to more energy harvested by sensor nodes,the system competitive energy consumption and transmission energy consumption are also increased.Figure5b shows that with the channel quality maintaining for a longer time,the system energy efficiency results in a slight decrease.Meanwhile,the increase of the Sink node's transmit power promotes the improvement of the system energy efficiency,as shown in Figure5c.The reason is a bigger transmit power compromises the poor channel quality.As the number of sensor nodes increases,the energy utilization rate of the system in the downlink phase decreases,so the system energy efficiency also decreases,as shown in Figure5d.The maximum delay of the system determines the maximum number of competitions,which means that the better channel can be obtained to some extent for downlink SWIPT.The relations between maximum delay and system gains are shown in Figure5e.The channel detection time affects the downlink SWIPT duration of the system,so that the increase of the detection time reduces the system energy efficiency,as shown in Figure5f.

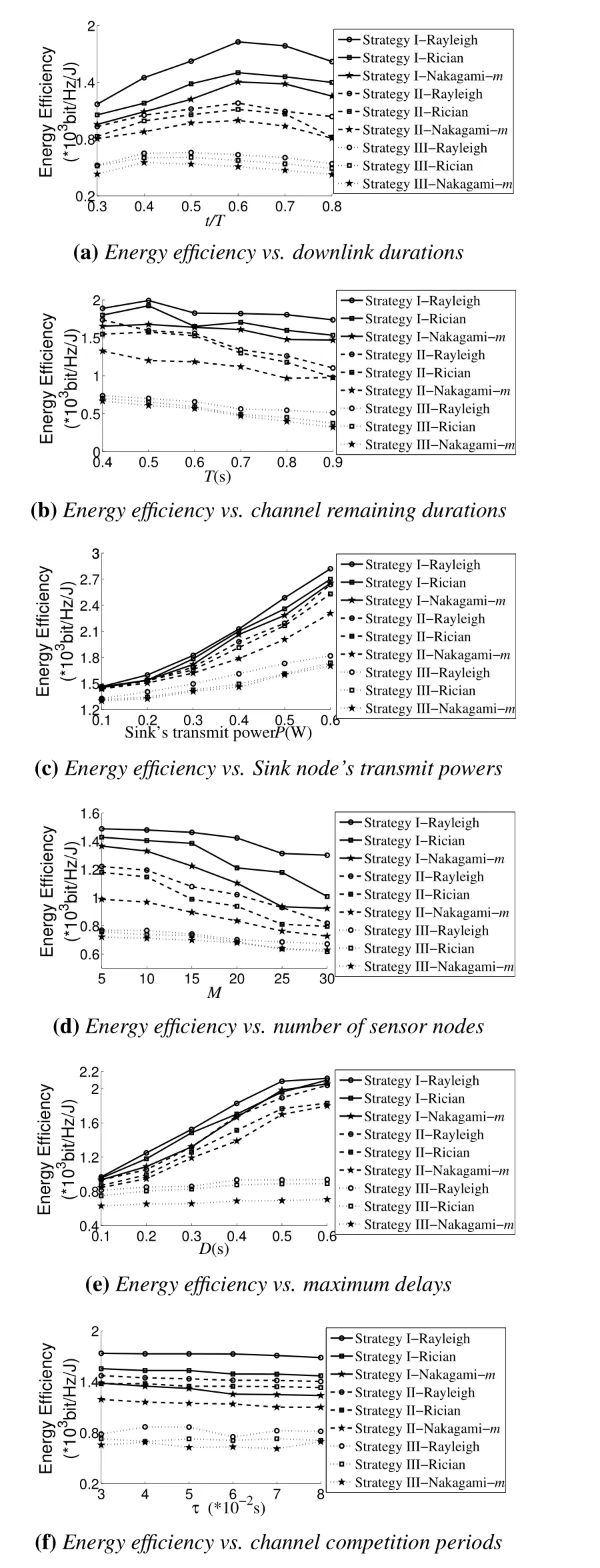
Figure5.Energy efficiency of the system.

VI.CONCLUSIONS

With the explosive growth of sensor terminals and cloud services,the energy conservation and emission reduction demand in the network are increasingly urgent.This paper focus on the energy efficiency of the SWIPT-enabled sensor-cloud network.Inspired by the COS and DOS,we design a system operation sequence where the Sink nodes in an interference network compete channel use for SWIPT in the downlink phase and collect data transmitted from the sensor nodes in the uplink phase.The problem is formulated as a system energy-efficiency optimization process with optimal stopping rules.Next,the optimal energy-efficiency algorithm is designed based on the optimal stopping theory to find the optimal stopping rules for the system.This work provides a distributed opportunity scheduling strategy for the energy harvesting communication networks,which overcomes the increase of transmission energy consumption caused by the time-varying of channel quality.In addition,the strategy can be further extended to other resource allocation cases,such as edge computing,internet of things and crowd-sensing.

ACKNOWLEDGEMENT

This work was supported by Scientific Research Ability Improving Foundation for Young and Middle-Aged University Teachers in Guangxi(No.2020KY04030),The school introduces talents to start scientific research projects (No.2019KJQD17).This work was supported in part by the National Natural Science Foundation of China (No.61762010,No.61862007),Guangxi Natural Science Foundation(No.2018GXNSFAA138147).

APPENDIX

Proof.A.Proof of the Theorem 1 According to[15],the optimal stopping rules of problem(12)exist if and only if the following conditions are satisfied

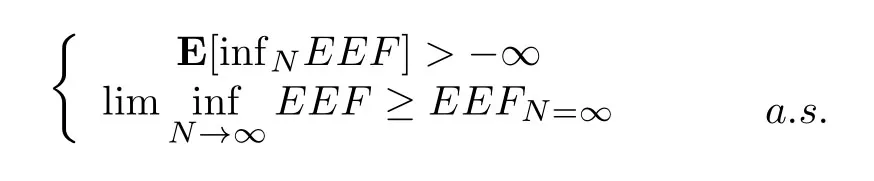
Due to the channel competitions count forN ∈{1,2,...,ND},and the channel gainsgmare the independent and identically distributed random variables with limited errors,theEEF ＞-∞is founded.Besides,the cumulative consumption for Sink nodes participated in the competitions tending to infinity as theN →∞,which makes the

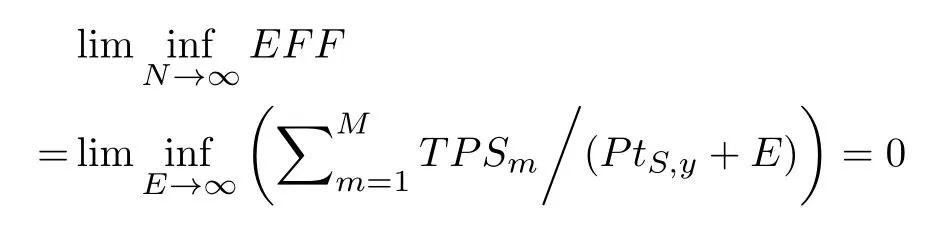
established.Hence,the condition limEFFN=∞is satisfied,which completes the proof.

Proof.B.Proof of the Theorem 2 Based on (12),it can be established that

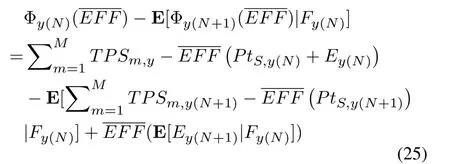
in which,E[Ey(Ny+1)|Fy(Ny)]is the expected energy competed for(Ny+1)-th competition.

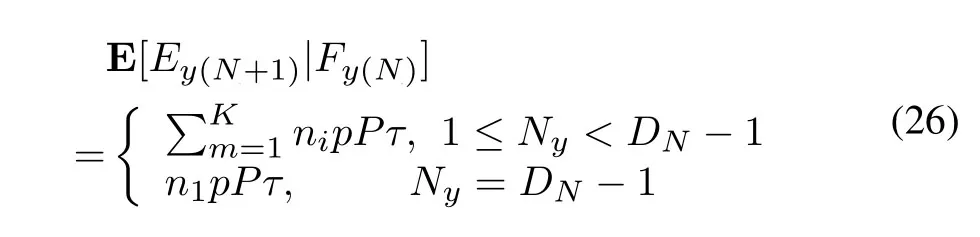
Due to the maximum delay of downlinkD,the Sink node starts SWIPT as soon as theND-th competition is successfully achieved.At present,the threshold of uplink throughput is zero,that is

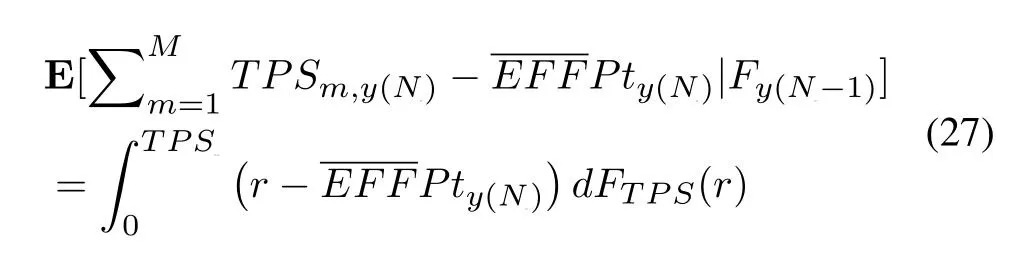
wheretS,y(ND−1)≤t - n1τ.Note that,the (28) is irrelevant to the transmission tasksy.This is because that different tasks influenced the system in the coefficientEFFandTPSmax.

Based on(28),the Sink node's throughput threshold for downlink SWIPT at(ND-1)-th successful competition is

Next,(29)can be rewritten as

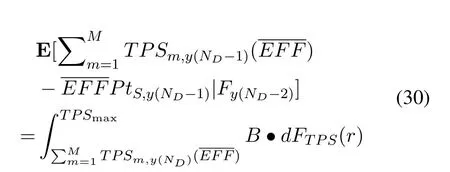
From(16),the Sink node's throughput threshold for downlink SWIPT at(ND -2)-th successful competition is

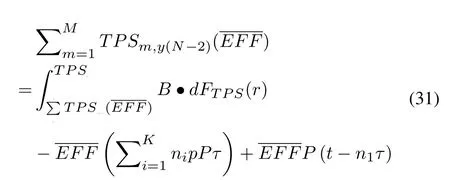
Repeat the above process,the throughput threshold of Sink node for SWIPT starts at (ND -3)-th,(ND-4)-th,...,1-th successful competition are separatelyFurther,it can be proved that the Sink node begins downlink SWIPT atNy-th competition successfully should satisfies the (17).In addition,that the (16)is monotonic as the Sink node's throughput satisfies the.Therefore,the stopping rules in Theorem 2 is optimal.