An Improved Equalization with Real Interference Prediction Scheme of the FBMC/OQAM System

Feng Yang,Yue Wang,*,Lianghui Ding,Liang Qian,2

1 Department of Electronic Engineering,Shanghai Jiao Tong University,Shanghai 200240,China

2 Shenzhen Institute of Guangdong Ocean University,Shenzhen 524088,China

Abstract:FBMC/OQAM transmission system has a better spectral efficiency than OFDM.However,its orthogonality condition is only considered in the real field.In the presence of fading channels,the real orthogonality of FBMC/OQAM might be lost,which calls for new equalization schemes.In this paper,an improved equalizer with real interference prediction (ERIP) scheme of FBMC/OQAM is proposed.We analyze the correlation between the real and the neighboring imaginary interference components taking Doppler shifts into account,and derive the improved ERIP scheme.The simulation results show that the proposed scheme can outperform the original ERIP and the one-tap equalization in time-varying multipath scenarios with an affordable complexity.

Keywords:equalization;ERIP;FBMC/OQAM;interference cancellation;time-varying multipath

I.INTRODUCTION

Orthogonal Frequency Division Multiplexing(OFDM) has been the popular transmission technique for many years due to its good performance and simple realization.Compared to OFDM,Filter Bank Multi-Carrier with offset quadrature amplitude modulation (FBMC/OQAM) further develops a time frequency well-arranged pulse shaping which can limit stopband energy and require no cyclic prefix(CP).Hence FBMC/OQAM has better spectral efficiency,higher-rate data transmission and looser synchronization requirements than OFDM[1-3].

FBMC/OQAM replaces the complex orthogonality feature of OFDM with real domain orthogonality.However,the complex nature of the real-world channel causes the real-orthogonality destruction that introduces intrinsic interference to FBMC/OQAM systems [4,5].Therefore,designing efficient equalizer for FBMC/OQAM with the time-frequency staggered structure becomes a hard but significant task.Many channel equalization techniques have been studied and developed for FBMC/OQAM while assuming time invariant or slow varying [6-10].There are a few papers focusing on the double selectivity problem[4,11].[11]proposed a simplified n-tap Minimum Mean Squared (MMSE) equalizer considering neighboring time symbols along with neighboring subcarriers.Based on[11],[4]further considered channel estimation errors and proposed a linear MMSE equalizer for high mobility scenarios with a slightly increased complexity.However,the MMSE equalizers have a high computational complexity,making them hard to be applied in practical systems.

[6]proposed an algorithm named Equalization with Real Interference Prediction (ERIP) which removed some residual interference after ZF by exploiting the imaginary interference to estimate the residual interference.Compared to MMSE schemes,it is more practical with much lighter online calculation.In this paper,we further improve this ERIP scheme for time-varying multipath scenarios.The improved ERIP schemes take neighboring time symbols as well as neighboring subcarriers into consideration and utilize their correlations with the current interference independently for interference cancellation.This paper is organized as follows.In Section II,we derive the analytical interference form in time-varying multipath channels,and analyze the interference correlation in a single path.In Section III,we improve the approach of ERIP and give the equations of necessary coefficients.Section IV shows the performance of improved ERIP in different scenarios.

Figure1.FBMC/OQAM baseband system model.

II.PRELIMINARY

2.1 System Model Of FBMC/OQAM

Based on the FBMC/OQAM modulation model depicted in Figure1,the continuous-time baseband transmitted signals can be written as[12]

wheream,nis the real-valued symbol atmth subcarrier andnth time symbol.The transmitted signal consists ofMsubcarriers andNstime symbols.v0is the subcarrier spacing withv0=1/2τ0,τ0the time spacing.g(t) is the impulse response of a symmetrical realvalued prototype filter with the length ofKM,Kthe overlapping factor.

A delay-Doppler impulse responseh(τ,v) [13]is used to represent the time-varying multipath propagation with delayτand Dopplerv.The received symbols can be expressed as

wherew(t) is the noise.After the demodulation,we suppose that the colored noise can be neglected according to[14].And the demodulated signalym0,n0is written as

where∗denotes the complex conjugation,p=mm0,q=n-n0.Ag(τ,v)is the ambiguity function ofg(t),defined as

In practice,the signal processing of FBMC systems is implemented in discrete-time.Using a sampling periodTs,we have 2τ0=MTs=2NTs.Then,the discrete-time representation of the demodulated signal is

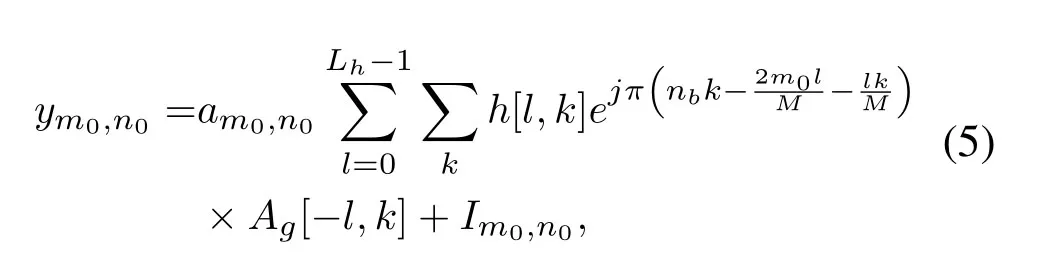
with

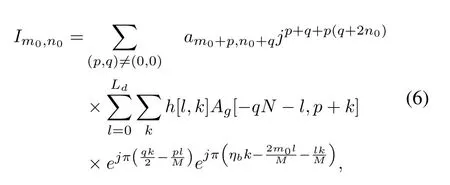
k=v/v0represents the normalized Doppler frequency shift,named as Doppler factor later in this paper.Equation(5)is divided into two parts:the useful part of the current time-frequency position andIm0,n0,the summation of ISI and ICI.

In addition,Ag[l,k]=Ag(lTs,kv0).Considering thatAg(τ,v)=Ag(aτ,v/a),a ∈R,a/=0 withg(t)normalized,the termAg[l,k]is free of the sampling periodTs.The ambiguity function reflects how the time and frequency selectivity influence the demodulated signal,lfor the time desynchronization,kfor the frequency desynchronization.Naturally,the power ofAg[l,k]is concentrated on the center point(l=0,k=0).To satisfy the real orthogonality condition,there isAg[2lN,2k]=0,(l,k)/=(0,0).When|k| ≥2,the frequency desynchronization is over two subcarrier spaces thatAg[l,k]is null as FBMC pledges that a sub-channel overlaps only with its neighbors in the frequency domain [15].And when|l| ≥KM,Ag[l,k]is null.

The coefficient of a 1-tap ZF equalization can be expressed as

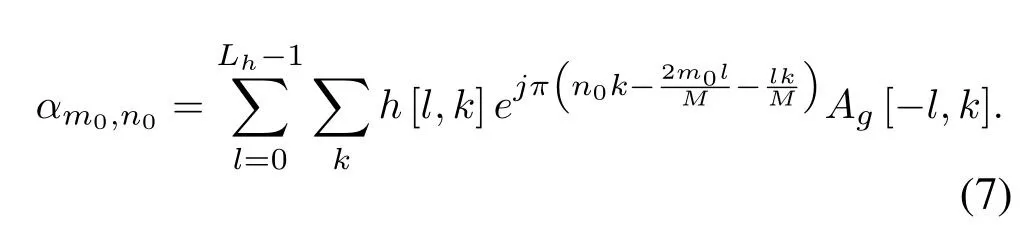
After the ZF equalization,the usual operation is to discard the imaginary component and take the real component as the equalization result.

2.2 Interference Correlation Analysis in A Simple Channel Model

The idea of ERIP is to exploit imaginary components which mainly contain interference to estimate the residual interference.In this part,we deduct the relationship between the real part and the imaginary part of the interference to find the imaginary components suitable for estimation.In order to make the interference correlation analytically tractable,we consider a single channel path withldthe delay in samples andkdthe Doppler factor.

After the ZF equalization,the interference in this case is

Its real part is written as

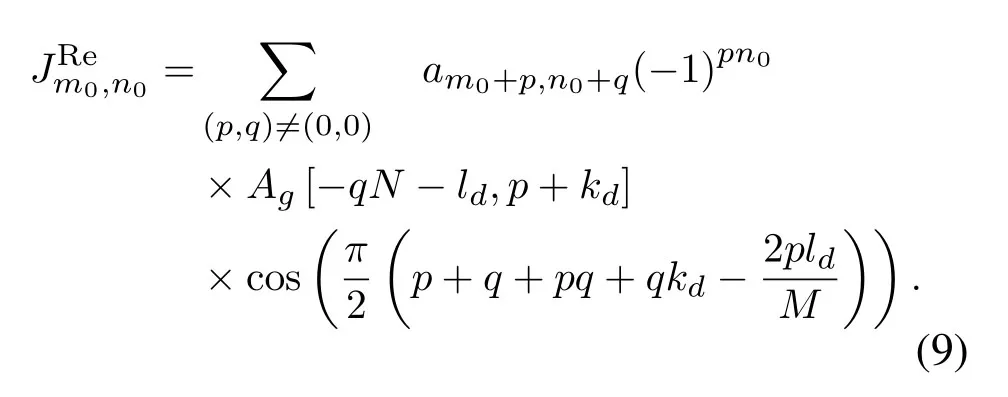
Its imaginary part is written as

We use RPI standing for the real part of interference (9),IPI for the imaginary part of interference(10).For an orthogonal prototype filter,we haveAg[2Nl,2k]=0 if (l,k)/=(0,0),l,k ∈Z.RPI is null when(ld,kd)=(0,0),and the real part extraction can be enough.When(ld,kd)/=(0,0),RPI still existing in the ZF result corrupts the demodulated symbols.

The covariance betweenJRem0,n0andJImm0+u,n0+twithuan integral subcarrier shift factor andtan integral time shift factor can be calculated by

whereσ2arepresents the variance of the real-valued zero-mean OQAM symbols.

The variance of RPI can be expressed as

Equivalently,the variance of IPI in this case can be expressed as

Then we can use the Normalized Correlation Coefficient (NCC) to find the correlation of RPI and a specific IPI.NCC can be calculated as

By plugging(11),(12)and(13)into(14)we can see that NCC is independent ofm0,n0in the single path situation.As a result,the NCC to be considered here is a function of four factors,the time shift factor,the subcarrier shift factor,the time delay,and the Doppler factor.The analysis of NCCs helps us identify the relative positions of IPI useful for RPI estimation.

The impact that negativekdmakes on sinusoids might lead to negative correlation.For this reason,we consider the absolute value of NCC (abs(NCC)).We setM=128,K=4 and have numerical tests to demonstrate positions suitable for RPI estimation.It should be emphasized that the precise NCC is also bonded by prototype filters.In this paper,we employ three prototype filters,which are respectively the frequency sampling (FS) filter,Hermite filter and rootraised cosine(RRC)filter with roll-off one[16,17].

First,we test abs(NCC) at different positions with randomly changingld ∈[0,10],kd ∈[-0.1,0.1].

In Figure.2(a) useful NCCs mainly appear atu=0±1 while Figure.2(b) NCCs appear symmetric to some extent.The omitted figure of RRC is like FS.Overall,FS owns better frequency selectivity and Hermite has better time selectivity.Both figures intuitively illustrate that abs(NCC)s are obvious in the four adjacent positions of the current position.And at (u,t)=(0,0),IPI has little correlation with RPI.Therefore,we can assume that the idea of ERIP has generality.

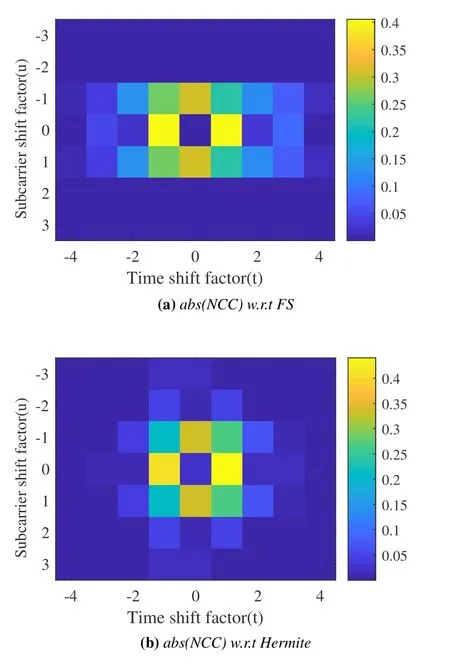
Figure2.The correlation distribution using different prototype filters.

As is stated in[6],the correlation based on the sum of IPIs at(u,t)=(0,±1)tends to decrease when the time delay increases,and the best frequency selectivity of FS yields this correlation higher than other filters.For the Doppler factor,we can also examine NCC with different filters at(u,t)=(1,0)in Figure3.

It is reflected in Figure3 that the Hermite filter owns the best time selectivity,and whenkd ＞0,NCC is relatively stable.If the channel is time-invariant,considering IPI at the adjacent subcarriers is needless due to tiny NCC.

III.THE IMPROVED ERIP SCHEME

In this section we improve the approach of ERIP and calculate related coefficients to adapt our scheme to time-varying multipath scenarios.

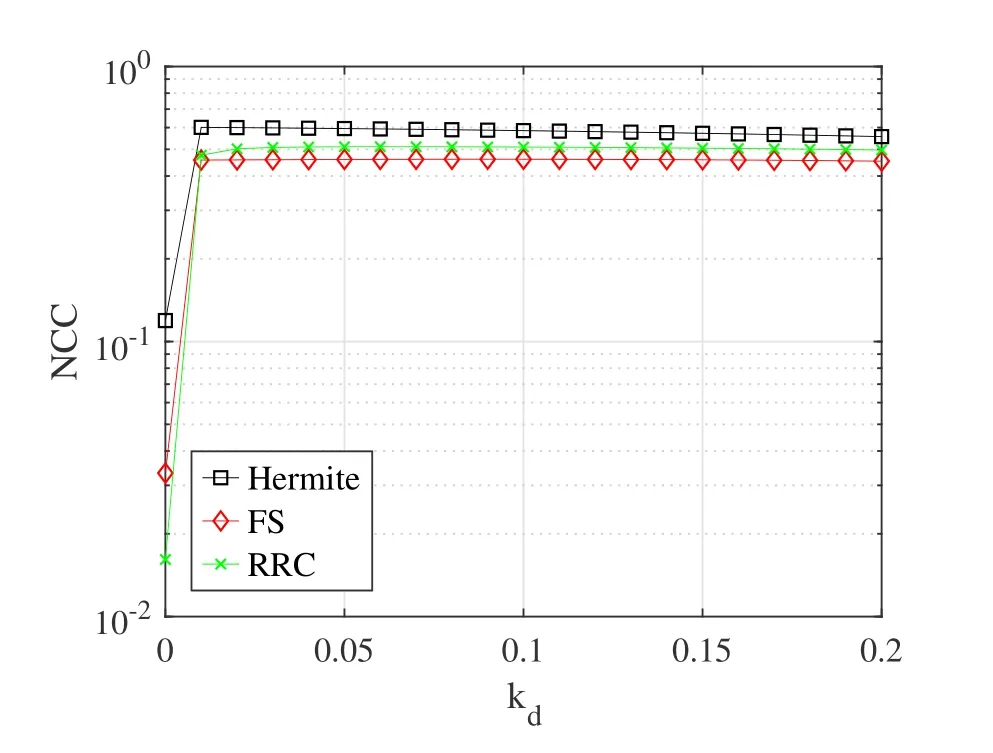
Figure3.NCC of different prototype filters at (u,t)=(1,0).

The linear regression method is the supporting theory of ERIP to predict RPI.The original ERIP uses two IPIs at (u,t)=(0,±1),and calculates the correlation between their sum and the current RPI.It is implied from our previous analysis that more positions and negative correlation should be considered for time-varying multipath scenarios.For this reason,we begin with the multiple linear regression model for RPI estimation.

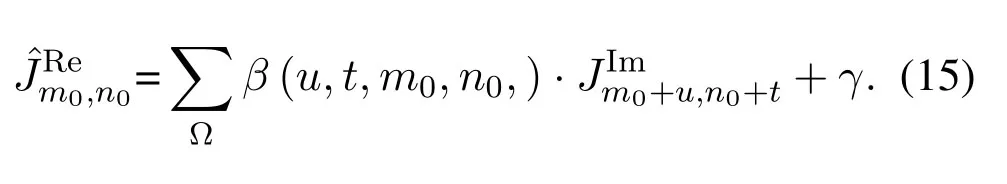
The value ofβ(u,t,m0,n0)is the regression coefficient which we can obtain.Ω represents the set including all the pairs of selected (u,t).Because both RPI and IPI are zero mean,the interceptγis zero.

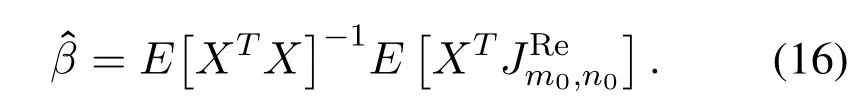
For the termEXTX−1,the variance and crosscorrelation of IPIs need to be calculated.For the termwe need the correlation between IPIs and RPIs,and we useC(u,t,m0,n0)to represent

Next,we start from(5),(6)and(7)for time-varying multipath scenarios.The interference at position(m0,n0)after ZF can be expressed as

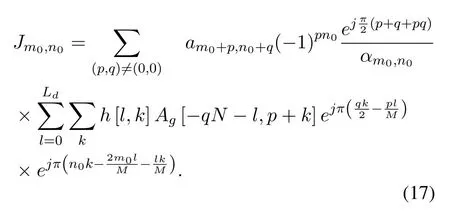
Let

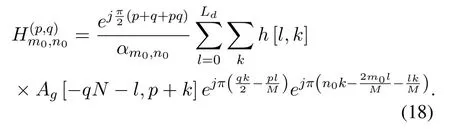
Then,we can get

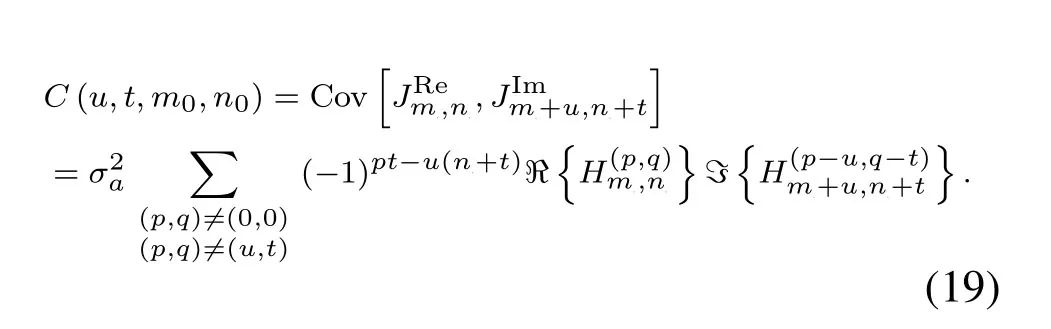
Also,we give the expressions of the variance and cross-correlation of IPIs,which are respectively

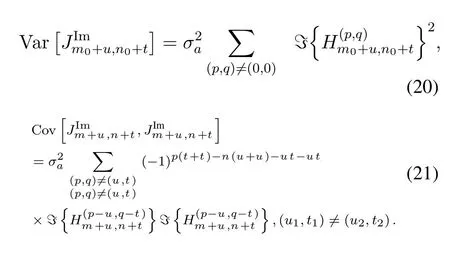
It is worth noting that the variance of IPI is depend on the specific position(m0+u,n0+t).

It is confirmed that the cross-correlation term (21)is usually much smaller than the variance (20) by numerical simulations.This enlightens us to simplify the equation (16) using the approximationEXTX≈diagEXTX.By neglecting the cross-correlation terms which have slight effects,the computation complexity can be greatly reduced.Finally,the RPI estimation in the multipath situation is written as

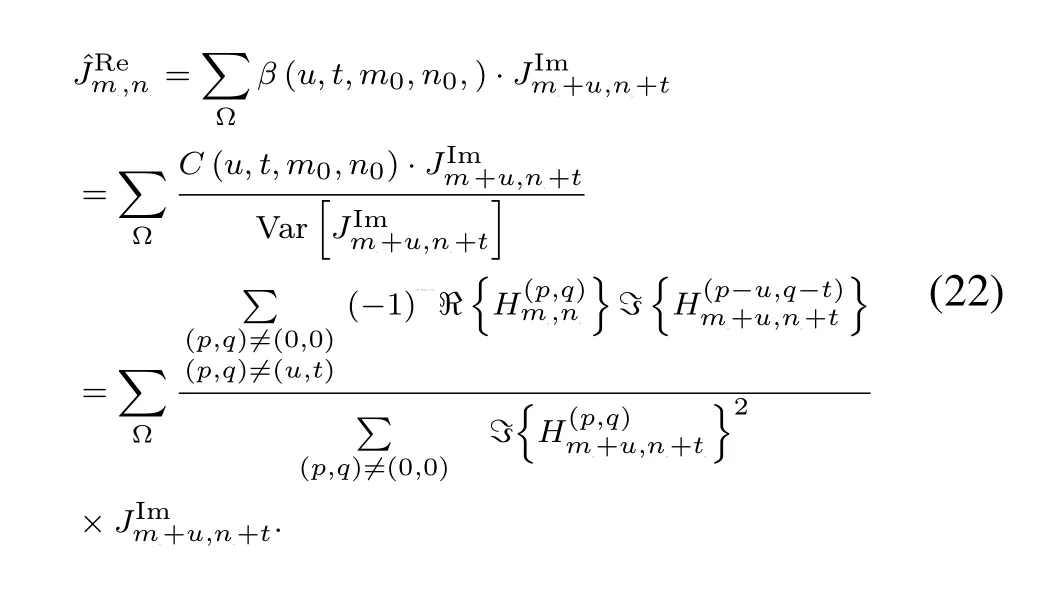
It should be figured out that we need not knowσ2ato estimate the RPI.

The proposed ERIP algorithm is summarized below.It contains the periodic calculation in Algorithm 1 and the online calculation in in Algorithm 2.The periodic calculation starts when the channel state information(CSI) is obtained in order to get the regression coefficients for each valid position.As the velocity and distance remain roughly the same for at least few milliseconds,the delay-Doppler representation can hold for a larger observation time[13].Apparently,the online calculation happens more frequently than the periodic calculation.At each position,the online calculation predicts and removes the RPI.And our structure is depicted in Figure4.

?

Several patterns designed for the set Ω are shown in Figure5.For the linear regression,when sample size is larger,the estimating precision is higher.

IV.SIMULATION RESULTS

?

Figure4.Improved ERIP structure.

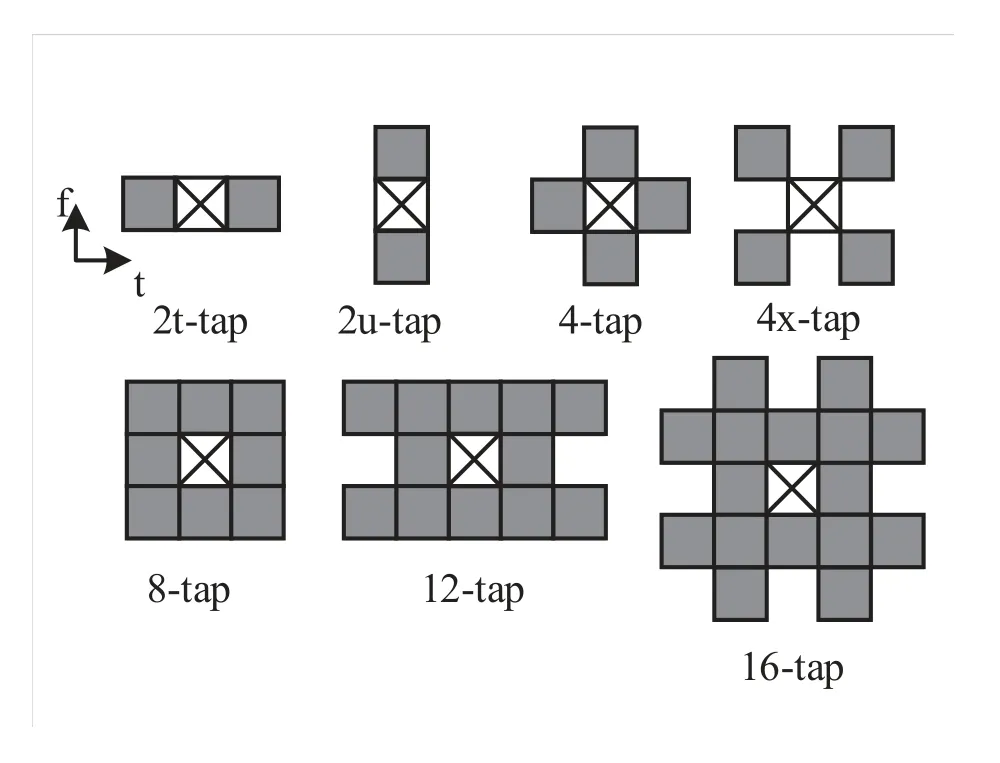
Figure5.Several patterns of the set Ω to estimate the RPI at the current position(indicated by the crossed in the center).

In this section,to compare our proposal with the former works,we discuss the computational complexity in the first part.In the second part,we simulate numerical performances of the improved ERIP,and we present achieved improvements with respect to Bit Error Rate(BER).

4.1 Complexity Analysis

For the periodic calculation,the ambiguity function can be prepared as a discrete table and we can get exact values directly or by interpolation.The major calculation cost depends on the set sizei,the numberRof the integer pairs (p,q) the path numberZh.The complexity of periodic calculation at each position is overO(iRZh).According to [6],the integer pairs can be restricted taking advantage of the saturation of correlation estimation.Nevertheless,Ris also related to the designed set due to the extension of patterns.In practice,(|p|≤3,|q|≤3) can serve all the set patterns designed in Figure5.Moreover,the delay-Doppler representation is usually compact and sparse,makingZhan acceptable number.

On the other hand,the ERIP scheme does the online calculation more frequently which hasimultiplications andi+1 additions at each position after ZF equalization.Compared to (i+1)-tap MMSE [11]of which the complexity is overthe online calculation of ERIP is much lighter.

4.2 BER Performance

We test the bit error rate(BER)in different scenarios by conducting Monte Carlo repetitions.In the following simulations,it is supposed that perfect CSI can be achieved.And we use the results of directly remove the accurate RPI as the lower bound of ERIP.The values of the unchanged simulation parameters are given in Table1.

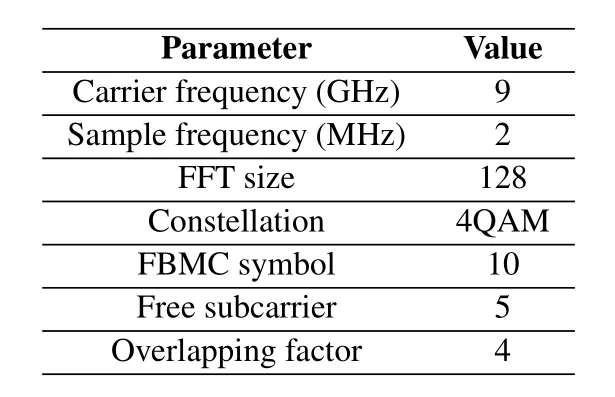
Table1.System parameters

A simple 2-ray channel and the Vehicular-B channel are adopted in our simulation.The 2-ray channel has the delay profile(in ns):[0,4500],along with the power profile (in dB):[0.0,-3.0].The Vehicular-B channel has the delay profile(in ns):[0,300,8900,12900,17100,20000]and the power profile(in dB):[-2.5,0,-12.8,-10,-25.2,-16].The Jakes model is adopted to modulate the time varying nature.We test different maximum Doppler factors.

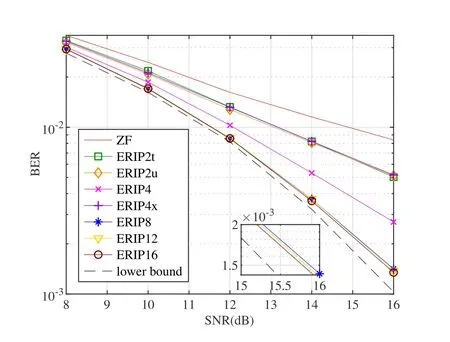
Figure6.BER comparison of the proposed patterns.

Figure6 compares the BER performance of different proposed patterns with respect to Figure5.The label ERIP4,for example,represents the improved ERIP of 4-tap.This simulation is carried out using the Hermite filter under the 2-ray channel with the maximum Doppler factor 0.2 (corresponding to the max speed 375km/h).The BER difference is significant in the high signal to noise ratio (SNR) regime.Generally speaking,there is a trade-off between the complexity and the performance.But the BER of ERIP4x is worse than that of ERIP4 in this scenario because the relative positions selected in ERIP4x is suboptimal.Besides,ERIP2t performs better than ERIP2u.The former is like the original ERIP,which indirectly reflects the effectiveness of the original ERIP.On the other hand,the curves of ERIP8,ERIP12 and ERIP16 come close to the ideal curve,but ERIP12 and ERIP16 only marginally improve the performance compared to ERIP8.Therefore,we suppose that ERIP8 is a good choice considering both the complexity and the performance,and we apply it to the following simulations.

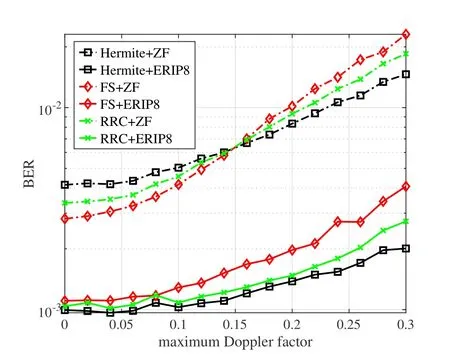
Figure7.performance using different prototype filters.

Figure7 shows the BER performance of different filters under the 2-ray channel with a fixed SNR value of 16dB.Two equalizers,ZF and ERIP8 are used.By observing the ZF performance,we can find that when the maximum Doppler factor does not exceed 0.15,the FS filter performs better than the Hermite filter and the RRC filter.But Hermite is best when the maximum Doppler factor is over than 0.15,which means for a fast time-varying channel,the Hermite filter is a better choice due to its more complex frequencydomain responses.The improvement of ERIP tends to be more apparent with greater maximum Doppler factor.Though ERIP8 scheme can improve the performance of all these filters,it is seen that the Hermite filter and the RRC filter can better utilize this scheme.The reason behind is that IPIs at the adjacent subcarriers of both own stronger correlation with the current RPI than the PHYDYAS filter.Overall,we suggest that the Hermite filter along with ERIP8 scheme is suitable for time-varying multipath scenarios.

Five schemes,ZF,original ERIP considering Doppler factors,our proposed ERIP8,9-Tap MMSE and Full Block MMSE are compared in Figure8.We select 9-Tap MMSE from [15]because its pattern is rather similar with ERIP8.Figure.8(a)employs a simple two-path channel with the maximum Doppler factor 0.1,which corresponds to the max moving speed 187.5 km/h.Our ERIP8 scheme is approximately 5dB better than ZF and 3dB better than the original ERIP at the BER of 10−3.Figure.8(b)employs Vehicular-B channel with the maximum Doppler factor 0.2,where the original ERIP can only get small improvement over ZF.Our scheme is approximately 4dB better than the original ERIP at the BER of 10−2.In this complicated case,IPIs from adjacent time symbols have a weak correlation with the current RPI.Using larger pattern would help us get more precise RPI estimation but significantly increase the complexity at the same time.However,9-Tap MMSE and Full Block MMSE can still work well as they use the real-time channel covariance matrix and the noise variance.Comparatively,our proposal can provide an easy and efficient implement.

Figure8.performance comparison with other schemes w.r.t Hermite.

In terms of the imperfect CSI,the performance of ZF is affected severely.In our simulations we find that ERIP8 can still improve the ZF results as a valid interference cancellation way when the bias is within 10%.

V.CONCLUSION

The ERIP scheme has been proved a suitable method in multipath situation without Doppler Effect to remove some residual interference after ZF.In this paper,we further improve ERIP to encounter measurable Doppler Effect and analyze its efficiency.Our improved method exploits the imaginary parts in neighboring time-frequency positions,and works better than ERIP in most scenarios,especially in time-varying multipath scenarios.Its mathematical derivation and simulation performance are provided.

ACKNOWLEDGEMENT

This paper is supported in part by NSFC China(61771309,61671301),Shanghai Commission of Science and Technology Funding(SCST 15DZ2270400),Shanghai Key Laboratory Funding (STCSM 18DZ1200102),and Medical Engineering Cross Research Foundation of Shanghai Jiao Tong University(YG2017QN47).