地铁轨道曲线半径与钢轨波磨的相关性研究*
陈晓丽 陈光雄 夏晨光 康 熙 黄之元
(西南交通大学摩擦学研究所 四川成都 610031)
截至2018年末,中国内地35个城市建成投入运营的城市轨道交通线路累计长度为5 766.6 km。进入“十三五”以来三年累计新增运营线路长度为2 148.7 km,年均新增线路长度716.2 km。在城市轨道交通的快速发展中,由于城市规划和用地限制等问题,导致城市交通轨道不可避免地出现小半径曲线轨道,这个区域段也是钢轨波磨的高发区域。
钢轨波磨[1]是在指钢轨轨顶面出现的有一定周期的纵向波浪形磨耗,它不仅使行车过程中产生强烈的振动和噪声,影响乘车的舒适性,还会造成轮轨间的不良接触,加剧轮轨间振动噪声,加剧联结零件和轮轴系统的失效进程,甚至影响行车安全。钢轨波磨每年的日常保养和维修更换都需要大量的资金投入,因此,研究钢轨波磨在小半径曲线轨道上的发展趋势,探索抑制或减少钢轨波磨的措施具有重要的科学意义和工程意义。
根据波长范围可以将钢轨波磨分为长波波磨和短波波磨,长波波磨指波长大于100 mm的波磨,短波波磨指波长在20~80 mm范围的波磨。波磨有2个重要参数,分别是波长和波深。通常情况下,波长越大,波深越大。
当前主流的波磨形成机制有两大类:第一类观点为钢轨表面的初始不平顺导致轮轨间瞬态动力学相互作用引起摩擦功波动,引起波磨机制[2-3];第二类观点为轮轨黏-滑自激振动导致钢轨波磨机制[4-6]。但是,依据观点一可推知,无论直线轨道还是曲线轨道、曲线的内轨或者外轨,发生钢轨波磨的概率是相等的,这一结论与实际铁路线路中钢轨波磨的典型现象不符。而根据观点二可以解释钢轨波磨通常出现在小半径曲线轨道上的这一现象 ,但不能解释在小半径曲线轨道上的钢轨波磨往往出现在内轨,而在外轨上很少出现波磨这一现象。
为此陈光雄教授提出轮轨摩擦耦合自激振动产生钢轨波磨的观点[7-13],该观点认为当轮轨间蠕滑力趋于饱和状态时,蠕滑力可以近似等于轮轨间的动摩擦力,即法向力与动摩擦因数的乘积,此时轮轨系统较大可能发生摩擦自激振动,从而导致钢轨波磨的产生。本文作者基于该观点,建立地铁小半径曲线轨道车辆曲线通过模型和轮轨系统摩擦自激振动模型,应用复特征值分析法研究轨道曲线半径对钢轨波磨的影响,探索曲线半径对钢轨波磨的影响机制。
1 轮轨接触模型
小半径曲线轨道轮轨接触情况如图1所示,车轮的名义滚动圆半径R=420 mm。外轮与高轨间接触角δL,内轮与低轨间接触角δR,轮对两端处受垂向悬挂力FSVL、FSVR和横向悬挂力FSLL、FSLR,轮轨间法向接触力NL、NR和蠕滑力FL、FR,均可由Simpack动力学仿真得出。
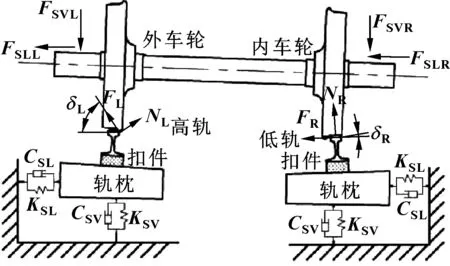
图1 小半径曲线轨道导向轮对-钢轨系统接触模型Fig 1 Contact model of leading wheelset-track system for curved tracks
钢轨与轨枕之间采用紧固件连接,由弹簧和阻尼元件模拟连接;轨枕由道床和路基支撑。道床和路基的组合刚度和阻尼也可以用弹簧和阻尼元件来模拟。对于钢轨支撑结构,其刚度、阻尼参数如表1所示。

表1 轨道支撑结构参数
1.1 复特征值分析
复特征值分析法一种研究摩擦自激振动问题的频域分析法。YUAN[14]提出在有限元模型中添加摩擦耦合作用,在不考虑摩擦力的情况下,摩擦系统的动力学方程为
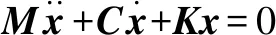
(1)
式中:x为位移矢量;M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵,且均为对称矩阵,因此方程(1)特征方程的特征值的实部不会为正,即系统是稳定的。
当考虑摩擦力时,系统的动力学方程转化为
(2)
式中:Mr、Cr、Kr分别为转化后的质量矩阵、阻尼矩阵、刚度矩阵,由于考虑了摩擦因素,均为非对称矩阵。
方程(2)的特征方程为
(3)
其通解表示为
x(t)=∑φkexp(λkt)
(4)
式中:λk=βk+jωk为方程(3)的特征值,βk、ωk分别为特征值的实部和虚部;φk是特征向量。
由于方程(3)中系数矩阵为非对称矩阵,则可能存在实部为正的特征值,表明系统有产生摩擦自激振动的趋势。通常用等效阻尼比作为判断轮轨系统稳定性的一个参数,定义如下:
(5)
当ξk为负数时,系统有产生摩擦自激振动的趋势,其绝对值越大,系统产生摩擦自激振动的趋势越大。
1.2 Simpack多体动力学模型
为计算出地铁车辆运行在曲线轨道时,在不同曲线半径轨道上轮轨间蠕滑力的变化情况,应用Simpack建立车辆轨道系统的多体动力学模型,如图2所示。该模型由1个车体、2个转向架和4个轮对组成。轮对和转向架之间采用一系悬挂,转向架和车体之间采用二系悬挂。
车轮踏面为LM型磨耗型踏面,钢轨型面采用CNH60型,选用60 kg/m钢轨,轮轨间动摩擦因数μ=0.4,轨底坡为1/40。轨道设置由50 m的直线轨道、50 m的过渡曲线和100 m的曲线组成。文中主要讨论前转向架导向轮对。

图2 车辆轨道动力学模型Fig 2 Vehicle track dynamics model
1.3 ABAQUS有限元模型
轮轨接触系统有限元模型如图3所示,它主要由3部分组成,包括1组轮对、2条轨道和58对轨枕。模型中单元类型均选用非协调单元C3D8I,单元总数为244 360,节点总数为340 357。钢轨长度L=36 m,两端为固定约束;标准轨距为1 435 mm;车轮踏面采用LM磨耗型踏面,车轮半径R=420 mm;模型中轮对的密度ρ=7.8×103kg/m3,弹性模量和泊松比分别为210 GPa和0.3;钢轨的密度ρ=7.79×103kg/m3,弹性模量和泊松比分别为205.9 GPa和0.3;轨道由固定的双短轨枕支撑,2个轨枕之间的间距为625 mm,轨枕密度ρ=2.5×103kg/m3,弹性模量和泊松比为35 GPa和0.2。钢轨与轨枕间的扣件约束(点对点)以及轨枕与道床间的约束(点对地)均用无质量弹簧阻尼单元进行模拟。垂直和横向悬挂力施加在轮对的轴端,利用复特征值分析计算系统振动的不稳定频率及其模态。

图3 轮轨系统有限元模型Fig 3 Finite element model of wheel-rail system
2 计算结果及分析
2.1 不同曲线半径下动力学分析结果
依据Simpack仿真结果,可以确定在不同曲线半径轨道情况下,轮对与钢轨之间的具体接触情形和受力分布。当平均速度为45 km/h(R=250 m)、50 km/h(R=300 m)、55 km/h(R=350~400 m)、60 km/h(R=450~800 m)时,分别计算内外轮轨接触系统的垂向悬挂力Q、横向悬挂力Y、纵向蠕滑力Tx、横向蠕滑力Ty、蠕滑力T与摩擦力F的对比、轮轨接触角以及轮轨接触法向力N。
施加在轮对轴端的垂向和横向悬挂力,即在车辆曲线轨道稳定运行状态下悬挂力的均值的计算结果见图4。图4(a)显示了内外车轮垂向悬挂力的变化情况,可以发现,内轮垂向悬挂力的变化趋势同外轮对称。图4(b)显示了轮对的内外轮横向悬挂力的演变,可见,内、外车轮上的横向悬挂力的演化趋势是一致的。在有限元模型中,轮对轴端只施加垂直和横向悬架力,且轨道完全光滑,因此在运行过程中得到的轮对轨道系统的不稳定振动是摩擦引起的振动。

图4 轴箱悬挂力随曲线半径的变化Fig 4 The variation of suspension forces with the radius of curve (a)vertical suspension forces;(b)lateral suspension forces
通过比较轮轨接触系统的蠕滑力合力和摩擦力,可以判断蠕滑力是否饱和。蠕滑力等于纵向蠕滑力和横向蠕滑力的合力。摩擦力等于法向接触力乘以摩擦因数,摩擦因数设为0.4。通过Simpack仿真,可以得到轮轨之间的法向接触力(见图5)、横向蠕滑力、纵向蠕滑力(见图6)。从而计算出轮轨间的蠕滑力和摩擦力,图7显示了在250~800 m曲线轨道半径处,内轮轨与外轮轨的蠕滑力饱和系数的变化。引入蠕滑力饱和系数(为摩擦力与蠕滑力的比值)可以更加直观地判断出轮轨蠕滑力饱和情况,当蠕滑力饱和系数大于0.95时可以认为轮轨间蠕滑力达到饱和状态。可以发现,在曲线轨道半径为250~400 m时,轮对内轮与低轨上的蠕滑力饱和;而外轮与高轨在曲线轨道半径为250~550 m时,蠕滑力处于饱和状态。
图8示出了不同曲线半径下导向轮对接触角的变化。可见,随着轨道曲线半径的增大,内轮与低轨的接触角逐渐增大,但增大的幅度很小,变化范围为2.20°~3.10°;随着轨道曲线半径的增大,外轮与高轨的接触角变化范围较大,为35.6°~11.4°。
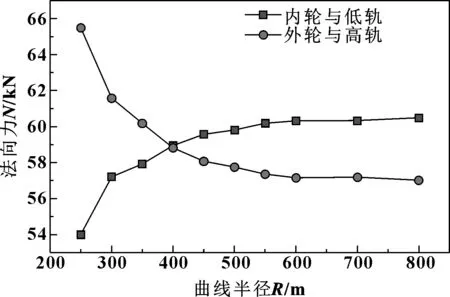
图5 不同曲线半径下导向轮对-钢轨系统法向力Fig 5 The variation of normal force of leading wheelset with radius of curve
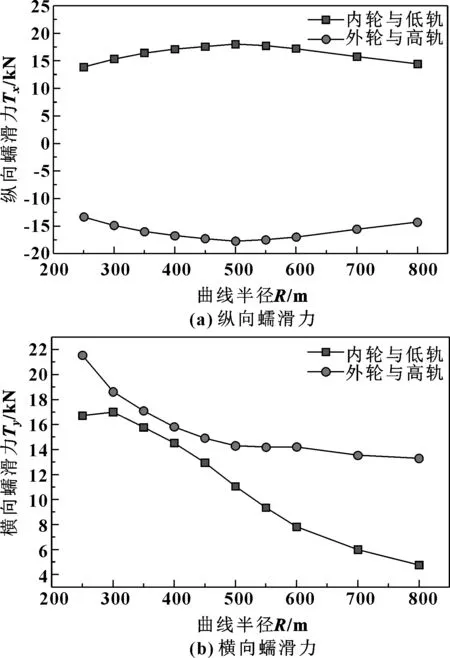
图6 导向轮对-钢轨系统蠕滑力随曲线半径的变化Fig 6 The variation of creep force with radius of curve(a) vertical creep force;(b)lateral creep force

图7 导向轮对轮轨蠕滑力饱和系数随曲线半径的变化Fig 7 The variation of saturation coefficient of creep force of leading wheelset with radius of curve
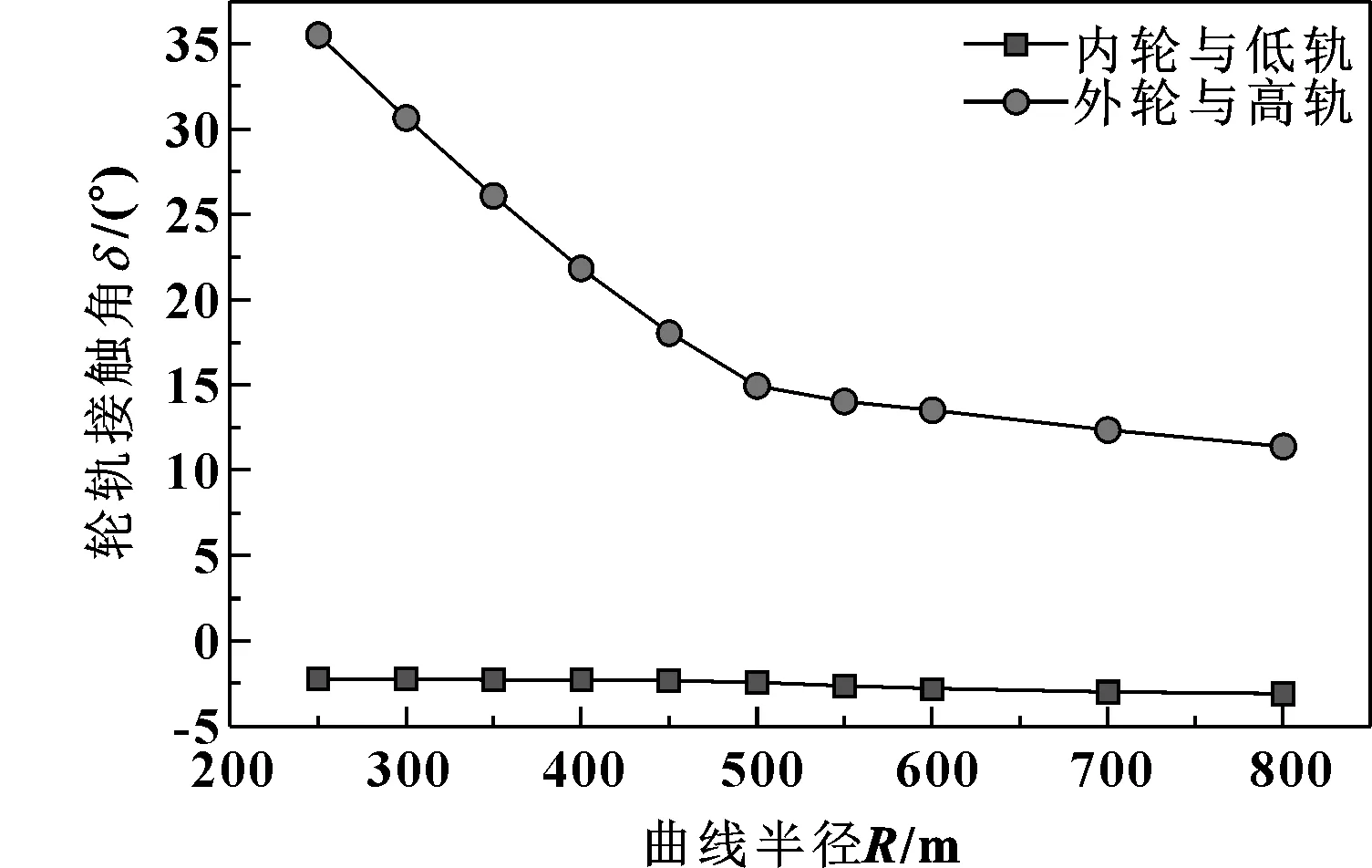
图8 不同曲线半径下导向轮对接触角的变化Fig 8 The variation of contact angle of leading wheelset with radius of curve
2.2 不同曲线半径下有限元分析结果
垂直和横向悬挂力施加在轮对的轴端,利用复特征值分析得到了系统振动的不稳定频率及其模态。用计算得出的等效阻尼比作为评价轮轨系统稳定性的重要参数。车轮-钢轨系统在负等效阻尼比情况下可能发生不稳定振动;此外,等效阻尼比越小,相应的摩擦自激振动就越容易发生。由于摩擦自激振动最容易发生在与绝对值最大的负等效阻尼比相对应的情况,因此需计算分析不同曲线半径轨道下负等效阻尼比的变化。图9显示了不同曲线半径轨道上导向轮轨的轮轨系统的等效阻尼比分布。
地铁线路小半径曲线轨道低轨上发生不稳定振动的频率范围为50~1 000 Hz,通过数值计算得到的波磨频率(如图9所示)基本上处于该范围内,说明数值分析结果和实际情况基本吻合,同时验证了轮轨间蠕滑力饱和引起轮轨系统摩擦自激振动导致钢轨波磨理论的正确性。近些年,大量学者对铁路上钢轨波磨的研究表明:曲线内轨一侧的轴箱振动比外轨一侧的轴箱振动更为剧烈[15],曲线轨道内轨波磨比外轨严重许多[16-20]。通过模态分析,轮轨系统的不稳定振动主要发生在内轮轨上,可以认为钢轨波磨主要发生在内轮-内轨系统,该仿真结果契合了车辆实际运行中的波磨产生现象。

图9 不同曲线半径轨道上的频率分布和对应模态Fig 9 Frequency distribution and corresponding modes shape for different curve radius(a) curve radius R=250 m;(b) curve radiusR=300 m;(c) curve radius R=350 m;(d) curve radius R=400 m;(e) curve radius R=450 m;(f) curve radius R=500 m; (g) curve radius R=550 m;(h) curve radius R=600 m;(i) curve radius R=700 m;(j) curve radius R=800 m
不同半径轨道下最小负等效阻尼比分布如图10所示,随着曲线半径值的增大,等效阻尼比的绝对值基本上逐渐减小。在曲线半径450~800 m时,没有产生负等效阻尼比,说明随着半径增大,不稳定振动减少,摩擦自激振动越不容易发生,钢轨波磨产生越少。此外,曲线半径为250~400 m的最小负等效阻尼比对应的主要不稳定振型都发生在内轮-低轨上。由此可以得出结论:曲线半径轮轨系统在内轮-低轨上摩擦自激振动强于外轮-高轨,即轮轨系统的钢轨波磨主要发生在内轮-低轨上。

图10 不同曲线半径轨道下最小负等效阻尼比分布Fig 10 Distribution of minimum negative equivalent damping ratio for different curve radius
3 结论
(1)当曲线半径小于或者等于400 m时,导向轮对的轮轨蠕滑力饱和,当曲线半径为400~450 m时,导向轮对的轮轨蠕滑力不饱和。
(2)在曲线轨道半径250~800 m范围内,内轮与低轨的接触角变化范围是2.20°~3.10°;外轮与高轨的接触角变化范围是35.6°~11.4°。
(3)当轮轨蠕滑力饱和时,轮轨摩擦自激振动主要发生在低轨上,而高轨几乎不发生摩擦自激振动,因而小半径曲线低轨极容易出现波磨,而高轨极少出现波磨。随着曲线半径的增大,内轮轨和外轮轨的蠕滑力都不饱和,摩擦自激振动发生概率基本很小,钢轨波磨产生的可能性也变得很低。

