含高渗透率水电机组的电力系统振荡参数的辨识分析

国网西藏电力有限公司电力科学研究院 西藏 拉萨 850000

1 基于自适应VMD(variational mode decomposition)与Hilbert变换的特征参数辨识

自适应VMD算法将系统的原始振荡信号f分解为K个IMF(intrinsic mode

function),对任意的IMF分量uk(t)进行Hilbert变换,即

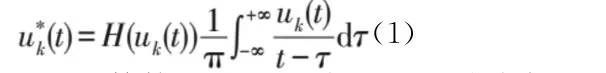
式中,H(*)为Hilbert运算符。以IMF分量uk(t)为实部,uk(t)的Hilbert变换u*k(t)为虚部,构造解析信号的表达式为

式中,Ak(t)和δk(t)分别为瞬时幅值和瞬时相位。IMF分量任意时刻瞬时频率函数fk(t)通过瞬时相位函数δk(t)求得

电力系统中的频振荡信号由一系列频率成分单一的模态响应叠加而成,对于频率成分固定的振荡响应信号可以表示为

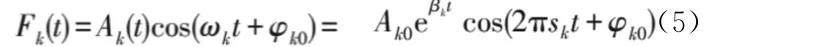
式中:Ak0为第k个振荡信号的初始幅值;βk为第k个振荡信号的衰减因子;sk为第k个振荡信号的振荡频率;φk0为第k个振荡信号的初相角。将式(2)与式(5)逐相对比分析,得到

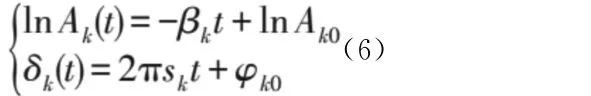
为求取该振荡模态下的衰减因子βk和振荡频率sk,对式(6)采用最小二乘法线性拟合;然后,利用βk和sk的计算结果求得对应模式的阻尼比,即

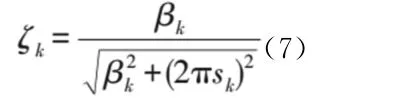
2 实际电网算例分析

本节以PSASP为仿真平台搭建水电机组算例仿真分析。图1为异步联网实验过程中,某大型水电站母线频率和5号机有功功率录波图。本次实验出现的振荡信号包含两组模态,其频率和阻尼比分别为0.362Hz、0.0658以及0.05Hz、0.0255。

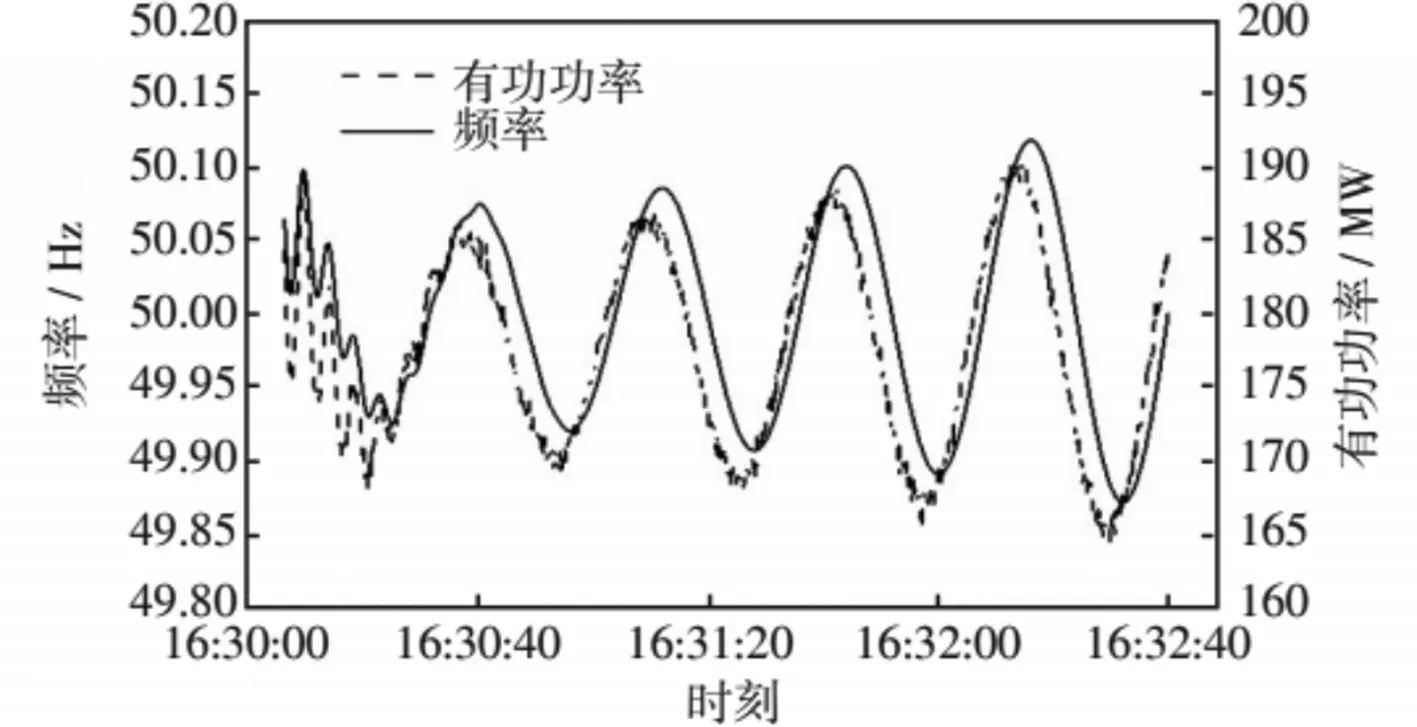
图1

采用自适应VMD算法和Hilbert变换对振荡频率进行特征参数辨识,得到的辨识结果与实验中振荡频率几乎相同,并与Prony滑动窗算法和ESPRIT算法的辨识结果进行对比,不同方法的辨识结果如表1所示,可见,本文方法无论在模态数量方面,还是频率和阻尼比方面都优于其他算法。

表1 不同方法的辨识结果

3 结语

本文采用自适应VMD算法和Hilbert变换对含高渗透率水电机组的电力系统中产生的低频振荡现象和超低频振荡现象进行特征参数辨识。本文方法可以有效地对振荡信号参数进行特征提取,提高了参数辨识的精准度。但没有讨论对振荡信号的抑制工作,这将是下一步的主要开展的研究工作。