基于有限元法和田口方法的翼子板成形工艺参数优化

王 兴，吴明明，王江龙

（1.安徽三联学院 机械工程学院，安徽 合肥 230601；2.合肥工业大学 机械工程学院，安徽 合肥 230009）

冲压成形受材料、模具设计、冲压设备等多因素的影响，会出现褶皱、破裂、拉毛、回弹等不同类型的成形缺陷。汽车前翼子板作为典型的冲压成型薄板零件，最大变薄率和最大增厚率是其评价目标，必须综合考虑，找出最优工艺参数组合，以保证零件成形质量。

对于冲压成形最大变薄率和最大增厚率的控制，国内外学者均有深入研究。文献[1]运用Dynaform 软件对翼子板的冲压成形进行了数值模拟，通过仿真得出汽车翼子板成形工艺及相应的优化方案。文献[2]利用田口方法，采用正交试验设计，就模具参数的稳健设计进行了分析。文献[3]采用基于有限元的田口方法确定不锈钢拉深成形过程中的工艺参数最优值，并找到这些参数对成形质量的影响。文献[4]通过Minitab 软件对冲压件各参数进行分析，利用稳健性设计原理找出最佳冲压方案再进行仿真试验。文献[5]利用田口方法结合Design-Exprt 软件对后围板冲压参数进行多目标优化，将最优工艺参数组合进行仿真验证，结果可以指导实际生产。

近年来，多种商用计算机仿真分析软件应用于塑性成形加工领域，为冲压加工的工程实际研究提供了有效保障，但是研究内容多集中在单一成形目标上。本文结合有限元法和田口方法，以某汽车翼子板冲压件为研究对象，依据目标函数和约束函数，通过寻找信噪比最大值确定最优参数组合，获得与实物成形一致性高的有限元仿真模型。

1 仿真试验设计

1.1 有限元建模

以某型轿车前翼子板拉深成形为研究对象，通过零件模型的中性面偏置产生凹凸模，再产生压边圈。冲压设备采用单动拉延机。图1 所示为翼子板有限元分析模型。

经调研企业的生产实际情况，选取板材DC04，板厚0.7mm，材料的力学性能见表1。

1.2 田口试验设计

考虑到多目标优化的需要，即兼顾最大变薄率和最大增厚率的双重影响，本研究设定最大变薄率和最大增厚率所占权重各为50%，作为综合评价指标考察翼子板的成形质量[6]。

依据板料成形过程中工艺参数对成形质量影响程度，选取试验因素为凹模圆角半径（A）、模具间隙（B）、摩擦系数（C）和压边力（D），考察目标为最大变薄率和最大增厚率。因素及水平取值见表2，表中t为板料厚度。

图1 翼子板有限元分析模型

表1 材料力学性能

表2 因素及水平表

利用田口试验设计原理，选取正交试验表L9(34)，根据试验参数确定试验组数。翼子板的冲压成形仿真数值模拟正交试验记录见表3。

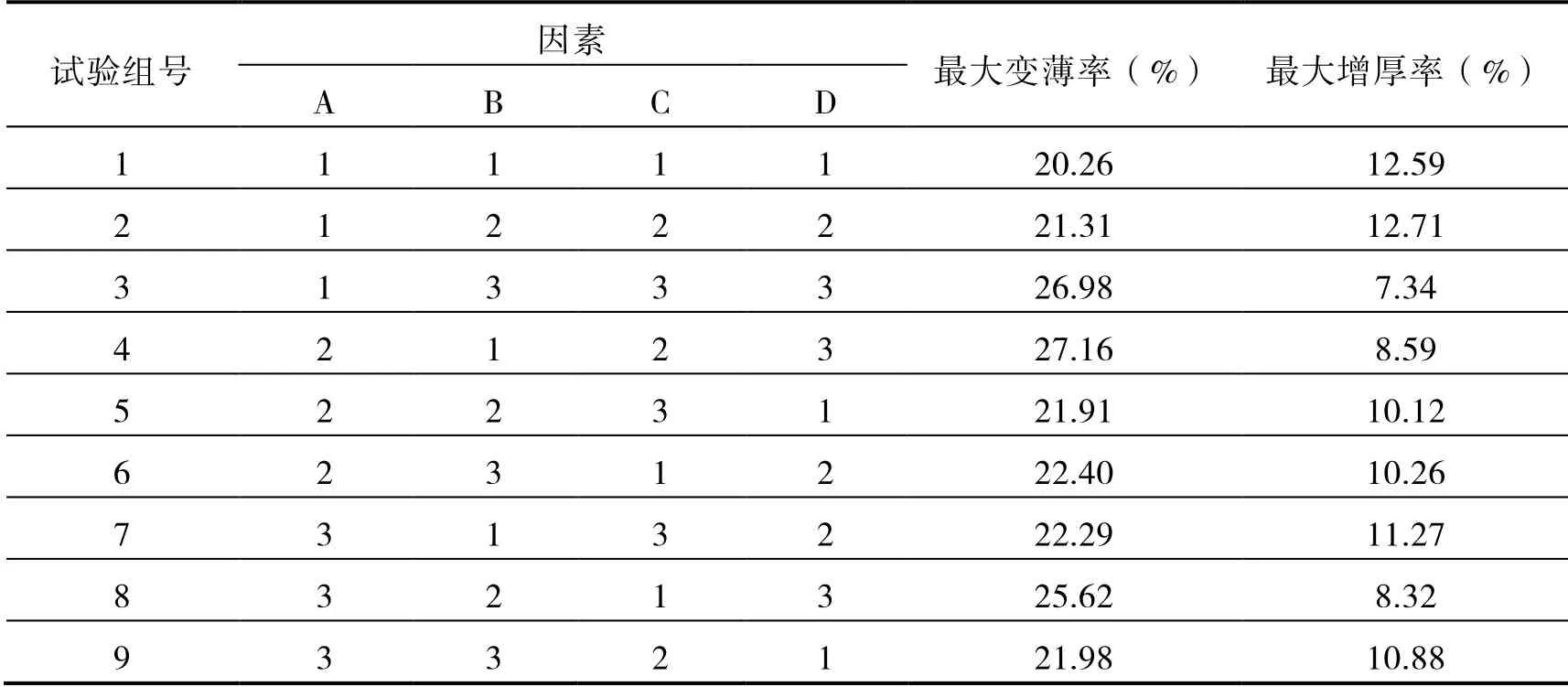
表3 翼子板的正交试验记录

2 结果与分析

2.1 试验结果描述

因田口试验中存在不稳定因素，多次试验所得的结果会存在偏差，故采用信噪比作为试验稳定性的评价标准[5]。信噪比是信号S和噪声N的比值，其计算方法如公式（1）所示。对于覆盖件的起皱和开裂现象，考察目标是最大增厚率和最大变薄率。在实际冲压工程中，希望它们的值在合理范围内越小越好，最大增厚率最好为零[6]，在田口试验中，这种情况称为望小值特性。从公式（1）可以看出信噪比是一个减函数，即信噪比的最大值对应目标的最小值。信噪比是田口试验中评判试验效果的重要依据。

式中：yi为第i次试验的结果，n为试验的次数。

综合信噪比S/N为：

2.2 信噪比分析

依据本文的优化目标，要求切边线内区域最大变薄率应小于30%，且越小越好；切边线内区域最大增厚率应不大于10%，且越小越好。

优化的目标：最大变薄率取极小值，最大增厚率取极小值。

约束的目标：最大变薄率<30%，最大增厚率<10%。

本试验利用Minitab 软件处理数据结果，并根据分析结果选择最优方案。信噪比计算结果见表4。

表4 信噪比计算结果

从表4 中可以看出，第3、4、8 组试验均满足优化目标函数的取值范围。而更高的信噪比意味着更好的质量特性，因此，最佳工艺参数组合对应最大信噪比。从综合信噪比计算结果表中可以观察出，第3 组试验的信噪比数值最大，为-22.9674，对应的最优参数组合为A1B3C3D3。即凹模圆角半径6mm、模具间隙0.77mm、摩擦系数0.13 和压边力110kN 时为最优的工艺组合，最大变薄率为25.98%，最大增厚率为7.34%，此时翼子板成形质量最佳。

采用上述分析得到的最优参数组合进行冲压成形，仿真模拟结果如图2 所示。通过成形极限图中的数据和模型，发现整体冲压模拟情况较好，尽管压料面上起皱，甚至强度不足，但是零件表面基本无缺陷，绝大多数位置处于临界区之下，可以顺利成形。只有左上角折弯处局部处于临界区，有破裂可能，但是该区域在激光切割线之外，所以不影响零件最终的冲压质量。另外，变薄率太低，零件就会刚度不足；变薄率太厚，容易产生堆积。从图3 可以看出，在零件边缘及中间区域选取7 个变薄率变化较大的特征点，获得对应的变薄率数值。发现零件上只有边缘及尾部少许部分变薄率超过了20%，而激光切割线以内零件区域的变薄率都不超过10%。同时，在最优成形工艺参数组合下，翼子板的最大变薄率和最大增厚率都符合工艺要求，制件成形质量在最大变薄率和最大增厚率之间取得了较好的平衡，可见优化组合的参数是合理的[7]。

图2 汽车翼子板成形极限图

图3 汽车翼子板变薄率分布图

（1）依据优化目标对零件表面最大变薄率的要求是取极小值，分析试验因素对最大变薄率的影响程度，通过信噪比响应表5 中的极差排秩可以快速确认因素影响从大到小依次是D、A、C、B。即压边力的影响最大，其他因素影响程度都很小。

表5 最大变薄率（%）信噪比响应

（2）依据优化目标对零件表面最大增厚率的要求是取极小值，分析试验因素对最大增厚率的影响程度，通过信噪比响应表6 中的极差排秩可以快速确认因素影响从大到小依次是D、B、C、A。依然是压边力的影响最大，其次是模具间隙及摩擦系数。

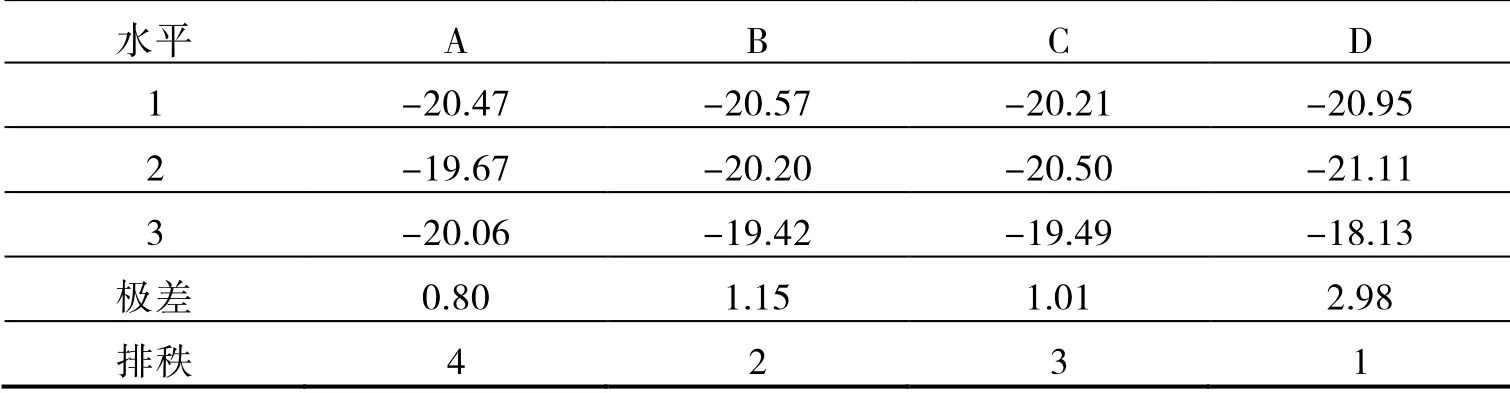
表6 最大增厚率（%）信噪比响应

（3）分析试验因素对综合信噪比的影响程度，通过信噪比响应表7 中的极差排秩可以快速确认因素影响从大到小依次是D、B、C、A。即压边力的影响程度最大，是最重要因素，其次是模具间隙及摩擦系数。

表7 综合作用下的信噪比响应

3 实物验证

根据上文田口试验获取的最优参数组合，设置现场设备工艺参数，完成实物冲压试验，切边完成后的翼子板零件如图4 所示。检查零件外观，没有发现明显的缺陷。为了进一步了解实物零件与仿真模型的成形一致程度，在实物零件与仿真模型表面相同位置标记7 个测量点，通过实际测量获得实物厚度与实物变薄率，对比结果如表8 所示。

图4 翼子板钣金零件

表8 测量点对比

通过对比发现，实物零件变薄率与仿真模型变薄率的最大差值是1.75%，根据目前对塑性加工问题进行仿真的水平，差值在10%以内都被认为是可以接受的合理结果[2]。因此可以判断，最优参数组合下的仿真模型是合理的，两者具有较高的一致性，如图5 所示。

图5 变薄率对比

4 结论

本文基于工程实际将田口方法运用于汽车翼子板冲压成形领域，设计了田口的L9(34)正交阵列开展有限元仿真试验。依据优化目标及约束目标，寻找综合信噪比最大值，确定最佳工艺参数组合，再使用这组参数进行实物冲压验证，并作对比分析，证明了最优参数组合下的仿真模型是合理的。