基于自适应滤波的水下长基线导航定位技术
成月,赵俊波,李锦,曹园山
(中国船舶科学研究中心 深海载人装备国家重点实验室,江苏 无锡 214082)
0 引 言
海洋在资源、经济、安全等方面具有战略意义,自治式潜水器(Autonomous Underwater Vehicle,AUV)作为一种新型水下无人运载平台,因其机动性、隐蔽性强,具备大范围搜索与探测能力,被广泛应用于海洋科考、海洋探测、海洋安全等领域。为保障AUV 在水下具备长航时作业能力,高精度、高可靠性的导航定位系统至关重要[1-3]。捷联惯性导航系统(Strapdown Inertial Navigation System,SINS)不受外界干扰,可在任何介质和任何环境条件下实现导航[4],一般作为AUV 导航定位系统的关键子系统。由于SINS 导航定位误差随时间累积,长期稳定性差,需采用外部辅助导航手段对其进行补偿修正,通过组合导航技术提高导航定位系统的整体性能。
水下主要采用声波进行导航定位,其中,长基线(Long Baseline, LBL)定位系统能够在较大的范围和较深的海水中得到较高的导航定位精度,利用LBL 辅助SINS 的组合导航技术是抑制误差发散、提高导航定位精度的有效手段[5-6]。LBL 定位通过测量布放在海底的应答器阵与AUV 上换能器之间的距离,求解AUV的位置坐标,再通过Kalman 滤波实现对惯导的校正。但由于水下环境多变,干扰因素复杂,组合导航系统精度难以保证。文献[7]采用异步量测序贯滤波方法提高了在应答信号缺失情况下组合导航系统的精度;文献[8]研究了SINS/LBL 紧组合系统量测方程非线性对定位精度的影响,选用UKF 滤波算法进行信息融合;文献[9]提出一种迭代声速修正算法,提高了LBL 在同步工作方式下目标定位精度。
这些算法主要集中在提高LBL 自身的定位精度及改进组合导航滤波算法,针对这两点问题,本文提出一种基于自适应滤波的水下长基线导航定位技术。一方面,研究基于伪距辅助的SINS/LBL 组合算法,解决水声通信时延导致LBL 定位系统位置坐标计算不准确的问题;另一方面,针对系统噪声统计特性未知问题,引入自适应滤波算法,通过改进组合导航系统信息融合方式,提高AUV 导航定位精度及系统可靠性。
1 伪距辅助的SINS/LBL 组合导航系统
1.1 系统原理及构成
LBL 定位系统是通过测量AUV 与海底应答器基阵之间的距离解算出目标AUV 位置坐标,其定位原理如图1 所示。

图 1 LBL 系统定位原理示意图Fig. 1Schematic diagram of LBL positioning system
LBL 海底应答器之间距离约100~6 000 m,其绝对位置坐标已知,主要用于接收声信号并发射不同频率的应答信号。AUV 上安装收发器,用于发射询问信号。当海底应答器基阵收到询问信号后,以不同频率应答。AUV 接收应答信号后,通过信号收发时间差即可计算出与相应应答器的距离,并通过球面交汇法或双曲面交汇法解算出AUV 位置坐标。
为实现水下高精度导航定位,AUV 组合导航系统以SINS 为关键子系统,LBL 定位系统为辅助系统。传统组合导航方式一般以LBL 解算出的位置信息作为量测量,通过Kalman 滤波校正SINS 系统。但在实际应用中,由于声信号在水中传播速度慢,随着AUV 运动将会产生时延误差,导致通过几何交汇进行位置解算的LBL 定位系统失效,且水下复杂的环境使得系统噪声无法精确建模,使用常规kalman 滤波无法得到最优估计,甚至会使组合导航系统误差发散。针对以上问题,本文设计基于自适应滤波的SINS/LBL 组合导航系统,以SINS 系统推算的伪距ρSINS与LBL 系统量测的伪距ρLBL之差作为组合导航系统量测量,并通过自适应滤波实现信息融合。系统结构如图2 所示。
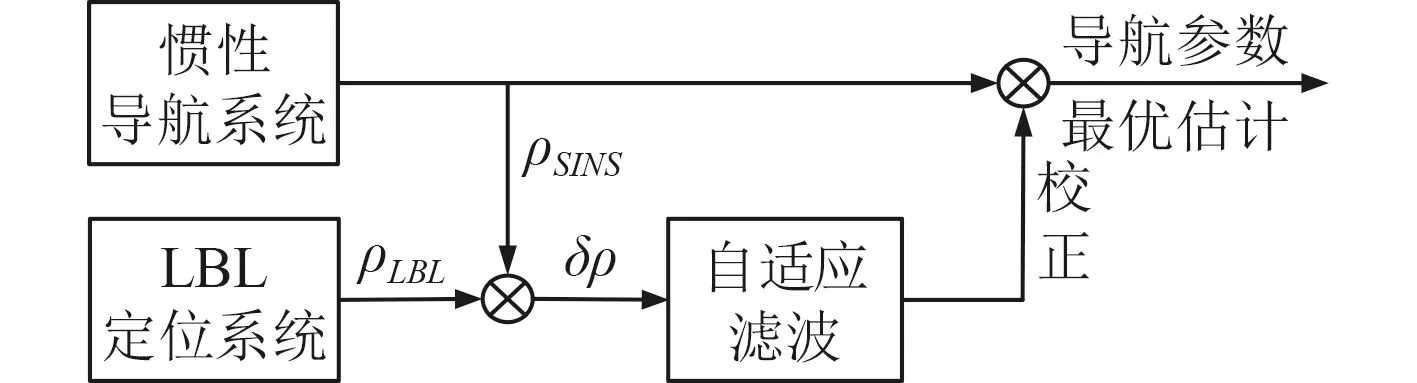
图 2 组合导航系统结构图Fig. 2Structure diagram of integrated navigation system
本节通过构建伪距辅助的SINS/LBL 组合导航系统解决水下时延误差对导航定位精度的影响,建立组合导航系统状态方程及量测方程。
1.2 状态方程
设AUV 真实位置为(X,Y,Z),海底应答器坐标为(xi,yi,zi),(i=1,2,3,4) ,为AUV 到第 i个海底应答器水声信号的传播时间,为AUV 到第 i个海底应答器的量测水声伪距,则有:
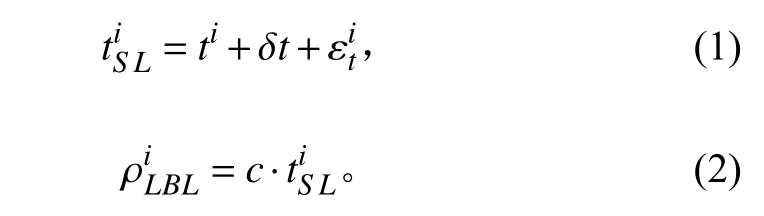
其中: ti为AUV 到第 i个海底应答器传播时间真值;δt为AUV 到海底应答器钟差;为 测量误差; c为声波在海水中传播速度。
δt的等效距离误差δtu可用一阶马尔科夫过程表示为:
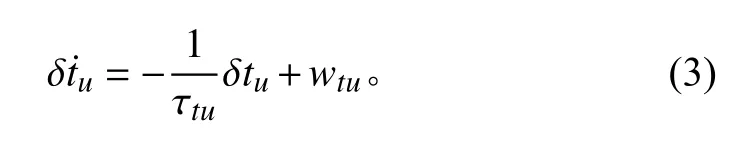
其中: τtu为 相关时间; wtu为白噪声。
对于SINS 系统,选取15 维状态量,分别是三维位置误差δL,δλ,δh , 三维速度误差 δ vE,δvN,δvU,三维姿态角误差 φE,φN,φU,陀螺漂移误差 εx,εy,εz,加速计偏置误差 ∇x,∇y,∇z,表示为:
XS INS =[φEφNφUδvEδvNδvUδL δλ δh εxεyεz∇x∇y∇z]T其状态方程为:
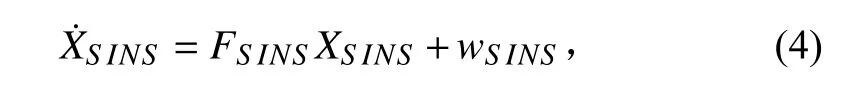
对于LBL 定位系统,选取等效距离误差 δtu为 状态量,其状态方程可表示为:

由式(4)和式(5)可得,伪距辅助的SINS/LBL组合导航系统16 维状态量表示为:
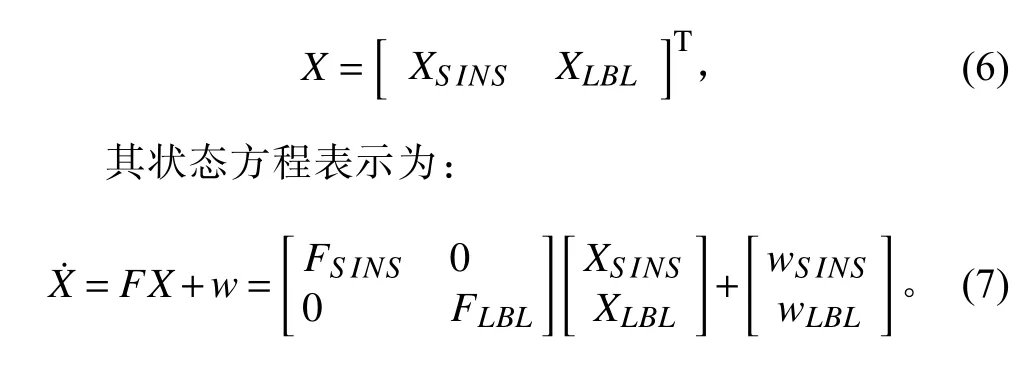
1.3 量测方程
由于水声信号时延,AUV 接收到海底应答器发出信号所在的位置并不一致,即采用几何交汇法无法解算出位置坐标。AUV 由惯导解算出的位置坐标表示为(xSINS,ySINS,zSINS),设 ti时刻AUV 接收到第 i个应答器的水声信号,以表示AUV 到第 i个应答器的伪距,则表示为:
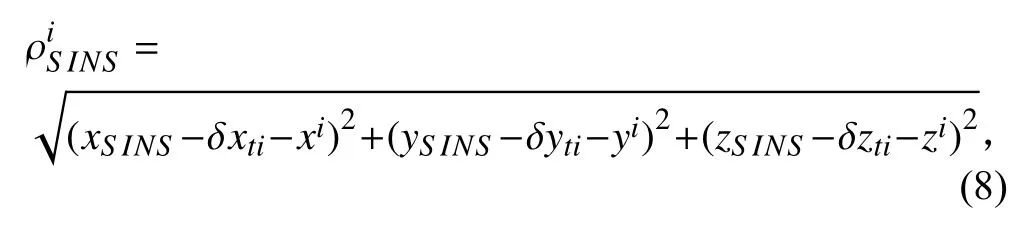
其中, ( δxti,δyti,δzti)表示为第 ti时刻起AUV 移动的位置增量,即需先计算得出AUV 在 ti时刻位置,然后进行伪距计算。
对式(8)在AUV 真实位置(X,Y,Z)处进行泰勒展开,伪距方程可简化为:

其中,Rii为AUV 到第 个应答器的真实距离。

伪距辅助的SINS/LBL 组合导航系统量测量表示为:
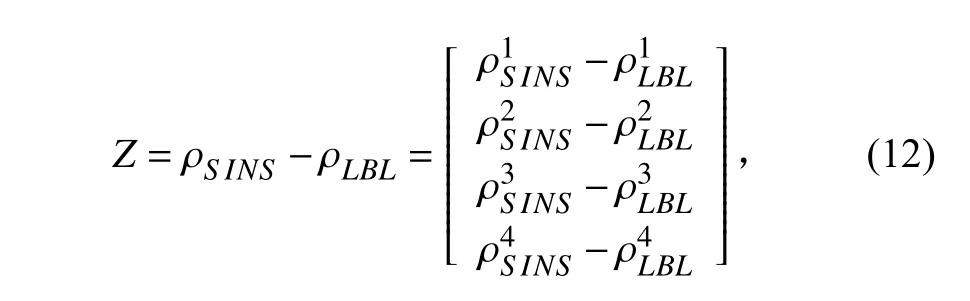
伪距辅助的SINS/LBL 组合导航系统量测方程表示为:e

其中,为卯酉圈曲率半径, 为旋转椭球扁率。
2 自适应滤波算法
组合导航系统通过滤波算法实现最优估计,传统的组合导航系统一般采用Kalman 滤波作为信息融合手段,但是Kalman 滤波需要构建噪声模型,由于水下环境产生的干扰复杂,往往无法对其进行精确建模,一般采用固定值直接带入滤波方程,这会极大影响Kalman 滤波的稳定性及组合导航精度。为此,本文采用自适应滤波算法估计组合导航系统误差,对系统量测噪声的协方差阵 R进行在线辨识,实现对AUV 姿态、速度、位置信息的最优估计。
式(7)、式(13)离散化后系统状态方程及量测方程如下:
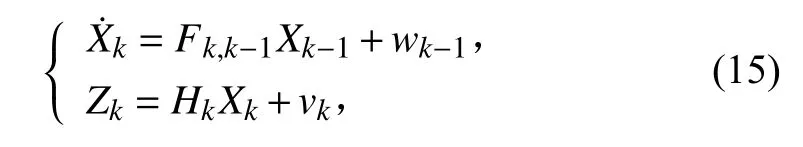
自适应滤波算法主要通过引入遗忘因子b ,不断强化量测量 Zk的作用,并削弱 Z1···Zk-1的影响,通过新息 εk在线估计协方差阵 Rk,并进一步优化滤波增益阵Kk,从而影响最终滤波结果。自适应滤波算法流程如下:

3 仿真结果分析
3.1 仿真环境及运动轨迹
设4 个海底应答器之间间隔1 000 m,AUV 初始姿态为(ψ,θ,γ)=(0,0,0),初始速度为 ( vE,vN,vU)=(0,0,0),初始位置为 ( λ,L,h)=(0,0,0)。采样频率100 Hz,总航时3 260 s。采用Matlab 对AUV 运动轨迹进行仿真,其三维运动轨迹如图3 所示。
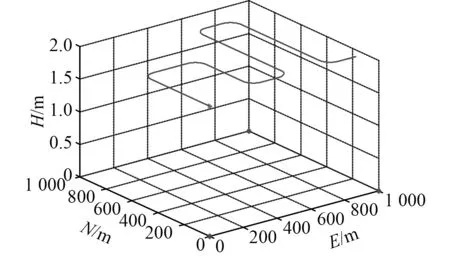
图 3 AUV 三维轨迹图Fig. 3AUV three-dimensional trajectory
3.2 仿真结果对比
在建立状态与量测方程的基础上,用Matlab 对本文提出组合算法进行仿真试验。考虑到惯导的高度通道发散,AUV 可直接通过深度计测量深度信息,故重点针对二维平面导航定位精度进行对比分析。AUV 依照图3 所示轨迹运动,在纯惯导算法及在伪距辅助的长基线组合导航算法下的二维平面仿真轨迹对比如图4 所示。

图 4 二维轨迹对比图Fig. 4Two-dimensional trajectory contrast diagram
由图4 可知,在3 260 s 的航时中,随着时间累积,惯性导航定位误差出现增长发散情况,导致纯惯导算法轨迹与真实轨迹出现千米级偏移量。这说明在无外界信息参考的情况下,仅依靠纯惯导无法满足AUV 水下导航定位精度要求。而在图4(b)中,伪距辅助的长基线组合导航算法由于提供了位置参考,抑制了惯导误差累积,其轨迹基本能够跟随真实轨迹,没有出现误差发散情况,导航定位精度较高。

图 5 速度误差对比图Fig. 5Velocity error contrast diagram
为进一步模拟水下复杂噪声干扰情况,仿真时增强量测噪声协方差阵 R,用以验证自适应滤波算法针对噪声统计模型未知情况下的修正能力及算法有效性。AUV 依照图3 所示轨迹运动,采用本文提出的基于自适应滤波的长基线导航定位算法与基于传统Kalman 滤波的长基线组合导航算法的速度、位置误差进行对比,仿真与分析结果如图5 和图6 所示。
可知,在噪声出现大幅变化的情况下,组合导航系统的信息融合算法将影响最终的导航定位精度。如图5(b)和图6(b)所示,由于量测噪声协方差阵R未知,仿真初始阶段误差震荡幅度较大。在航行时间2000 s 后,由于自适应滤波算法对 R进行在线估计,采用自适应滤波算法的长基线组合导航系统误差基本收敛,其东向、北向速度误差在±0.05 m/s范围内波动,东向、北向位置误差在±10 m范围内波动。对比图5(a)和图6(a),在航行时间2 000 s 后,采用传统Kalman 滤波算法的长基线组合导航系统的东向、北向速度误差达到-0.1 m/s,且有发散趋势,其东向位置误差达到 - 15 m,北向位置误差达到 - 27 m。这说明在环境噪声干扰较强时,即使采用长基线通过位置校正惯导,也无法达到高精度导航定位要求,甚至无法确保系统的导航定位误差收敛。

图 6 位置误差对比图Fig. 6Position error contrast diagram
4 结 语
本文提出一种基于自适应滤波的水下长基线导航定位技术,通过伪距辅助的长基线组合导航系统对惯导进行校正,防止导航误差随时间累积;通过自适应滤波算法对噪声进行在线辨识,实现对系统导航定位参数的最优估计,提高系统的导航定位精度及可靠性。仿真结果表明,面对水下复杂的噪声干扰,本文设计的水下组合导航算法具有较强的抗干扰性能,并能够满足AUV 水下长航时、高精度的导航定位要求。

