多尺度函数的平衡性与Armlet的研究
陈韫智,王 刚
(新疆师范大学 数学科学学院,乌鲁木齐 830017)
近年来,小波变换成了重要的分析工具。小波处理技术被广泛应用,小波理论得到良好发展。然而单小波在应用上存在先天不足,对称性、正交性等性质不能共存。人们不断探索希望可以摆脱单小波开发的局限性,多小波得到了良好的发展。[1]但在多小波的应用中需要进行预滤波,这个操作往往会损坏多小波结构。[2]平衡多尺度函数得到推广[3],在处理多小波应用中发挥了巨大优势,特别是处理多项式信号,效果显著。[4]C-L提出了Armlet多小波,解决了预滤波问题。本文从多尺度函数[5-6]的角度出发,结合多小波Armlet的存在条件,对特定算法[7]构造出的正交多小波进行PTST(仿酉两尺度相似变换),给出平衡多尺度数对应多小波函数是Armlet,并讨论了正交对称的情况,最后给出一种算例。
令Φ(x)=[φ1(x),φ2(x),…,φr(x)]T是r重多尺度函数,满足
(1)
且Ψ(x)=[ψ1(x),ψ2(x),…,ψr(x)]T是对应的正交多小波,满足
(2)
整理式(1)和式(2)得

(3)
(4)
(5)

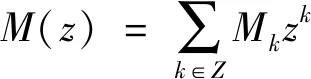
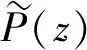
(6)
其中:P(z)存在的基础条件是:(a)矩阵P(1)满足条件E,即1是P(1)的简单特征值,其他的特征值的模都小于1;(b)存在向量γ0,γ0P(e-ikπ)=δk,0γ0,k=0,1。
定义2 设Φ(x)=[φ1(x),φ2(x),…,φr(x)]T是多尺度函数,P(z)是其对应的两尺度矩阵符号,且Ψ(x)=[ψ1(x),ψ2(x),…,ψr(x)]T是对应的多小波,Q(z)是它的两尺度矩阵符号。若
〈φi(x),φj(x-k)〉=δi,jδ0,k,〈φi(x),ψj(x-k)〉=0,〈ψi(x),ψj(x-k)〉=δ0,kδi,j,
其中:i,j=0,1,…,r-1,则称Φ(x)是正交的多尺度函数,Ψ(x)是对应的正交多小波。它们的两尺度矩阵符号满足
(7)
根据两尺度矩阵序列{Pk}定义Band-Toeplitz矩阵L
定义3 称正交多尺度函数Φ(x)是平衡的,如果LTμ0=μ0(低通合成算子LT能保持μ0信号不变),其中:μ0=[…,1,1,1,1,1,…]T。
引理1[1]假设正交多尺度Φ(x)是平衡的,则B1,B2,B3是等价的:
定义4 设Q(z)是正交多小波Ψ(x)=[ψ1(x),ψ2(x),…,ψr(x)]T的两尺度矩阵符号,称Ψ(x)是n阶Armlet多小波,(1-z)n|Hi(z),i=1,2,…,r,其中相位矩阵
[H1(z),H2(z),…,Hr(z)]T=Q(zr)[1,z,…,zr-1]T。
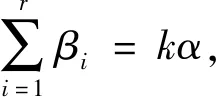
1 特殊多尺度函数和Armlet多小波
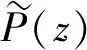
根据引理3知,若Φ(x)是m逼近阶的正交非平衡,则通过PTST可以平衡Φ(x)。
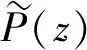
[1,1,…,1]M=kα或MT[1,1,…,1]T=kαT,
(8)
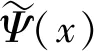
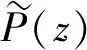
(9)
引理5[1]设Φ(x)=[φ1(x),φ2(x),…,φr(x)]T是多尺度函数,P(z)是两尺度矩阵符号。Ψ(x)=[ψ1(x),ψ2(x),…,ψr(x)]T是对应的多小波,Q(z)是两尺度矩阵符号。假设0是Q(1)的一个特征值,相应的特征向量是γ=[γ1,γ2,…,γr]T,数字矩阵M是r×r的正交矩阵,且MT[1,1,…,1]T=λγ,构造PTST(仿酉两尺度相似变换):
(10)
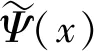
相应的两尺度符号是
(11)
从引理5中知道构造Armlet多小波PTST时需要正交矩阵M,而由引理3知道通过PTST平衡Φ(x)需要变换矩阵M0。现在需要得到对应的Armlet多小波,就要满足引理3与引理5中的变换矩阵是相同的。
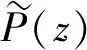
引理6 设φ1(x)是正交单尺度,而ψ1(x)是对应的单小波,则有p1(ω),q1(ω),p2(ω),q2(ω):
(1)s(ω)h(ω)≠0,(2)s(ω),h(ω) 是以π为周期的函数,(3)|s(ω)|2+|h(ω)|2=1,定义

那么P(ω),Q(ω)分别生成了正交的2重多尺度函数与多小波。

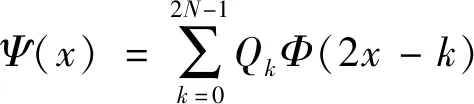
对重数r=2n为偶数的情形,分别是
根据引理4的条件讨论。设S=diag(1,…,1,-1,…,-1),1与-1个数都是n的情形,

(12)
(13)
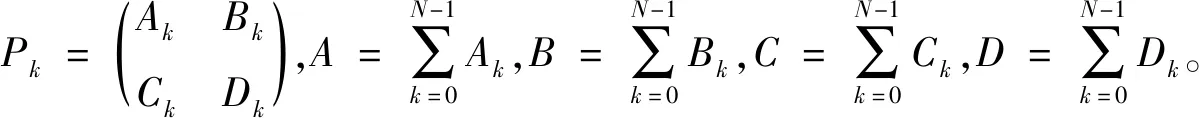
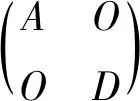
2 构造算例
例1 基于文献[11]的例子。
设Φ(x)=[φ1(x),φ2(x)]T,Ψ(x)=[ψ1(x),ψ2(x)]T,构造
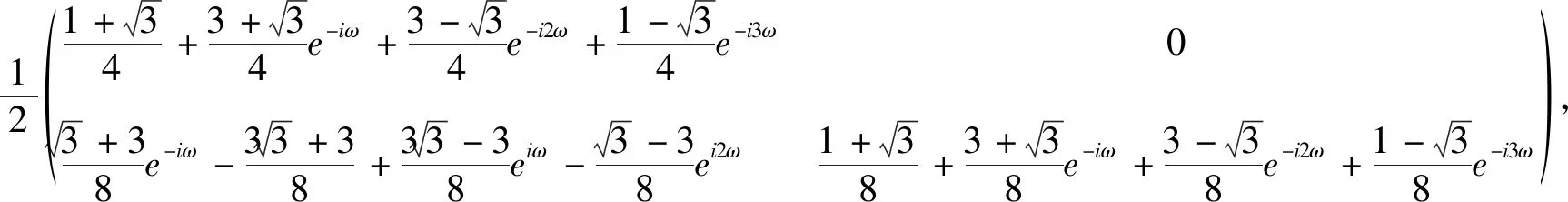

由于
则Φ(x)不是平衡的,且Ψ(x)也不是Armlet。取
则

