Liouville方程与其约化变换方程的精确解及ψ(ξ)展式法

林府标, 张千宏

(贵州财经大学 数统学院, 贵阳 550025)

0 引 言

Liouville方程

uxt=eu

(1)

是流体力学中的一个经典非线性偏微分方程, 其精确解的动力学行为已得到广泛关注. 文献[1]给出了方程(1)可接受的无穷小李对称； 文献[2-3]给出了方程(1)的一些精确解. 目前, 显式解析波解及其特征在海洋工程、 光纤通信、 材料科学和流体力学等领域应用广泛[4]. 虽然人们已经构造了一系列解析求解非线性偏微分方程的有效方法, 如齐次平衡法[5-7]、 tanh函数法和广义tanh函数法[3,8-10]等, 但因非线性偏微分方程的多样性和复杂性, 至今仍有一些重要的方程无法采用现有的方法和技巧得到精确解. 本文用Liouville方程(1)的约化变换方程及其精确解构造一种精确求解非线性偏微分方程的有效ψ(ξ)展式法, 并用该方法寻找Kawahara方程和(3+1)维Kadomtsev-Petviashvili方程的显式新行波解.

1 Liouville方程的群不变解和精确解

1.1 Liouville方程的群不变解

Lie[1]给出了Liouville方程(1)可接受的李对称, 并由下列一组基生成：

其中ξ(x),η(t)为任意函数,X∞为无穷李对称. 根据文献[11]中算法, 可写出三维李代数L3=span{X1,X2,X3}的换位子交换运算, 结果列于表1.

表1 三维李代数L3的换位子交换运算表Table 1 Commutator exchange table of three-dimensional Lie algebra L3

由表1可得相应的内自同构为

求其对应的李方程可得群变换

其中σi(i=1,2,3)分别为内自同构Ai(i=1,2,3)的群参数. 因此, 对任意的实数c, 李代数L3的最优化三维、 二维和一维子李代数分类结果分别为span{X1,X2,X3},span{X1,X2},span{X1,X3},span{X2,X3},span{X1},span{X2+cX1},span{X3}. 用L3的一维最优化子李代数可得方程(1)的群不变解, 结果列于表2, 其中一维子李代数span{X1}对应的群不变解未找到.

表2 方程(1)的群不变解和约化方程Table 2 Group invariant solutions and reduced equations of equation (1)

1.2 Liouville方程的新行波解

若令变换u(t,x)=ln(v(t,x)), 则有uxt=v-2(vxtv-vxvt), 因此把uxt和u代入方程(1)可得

vvxt-vxvt-v3=0.

(2)

做行波变换ξ=x-ct, 其中c为常数, 表示波速. 若假设v(t,x)=V(ξ)为方程(2)的解, 则方程(2)可约化为常微分方程

cVV″-cV′2+V3=0.

(3)

用广义tanh函数法[3,8-10]并结合齐次平衡原理[5-7], 再注意到平衡项VV″与V3, 可假设方程(3)解析解的表达式为

V(ξ)=b0+b1φ(ξ)+b2(φ(ξ))2,

(4)

其中:bi(i=0,1,2)为待定常数;φ=φ(ξ)满足方程φ′=b+φ2,b为任意实常数. 将式(4)代入方程(3), 反复利用方程φ′=b+φ2并结合软件Reduce计算整理可得关于φ的多项式, 于是可分别令φj(j=0,1,…,6)的系数为零, 可得关于bi(i=0,1,2),b,c的代数方程组为

用吴消元法[12]并结合Reduce计算可得一组解b0=-2bc,b1=0,b2=-2c. 因此, 方程(1)的行波解为

u(t,x)=ln(-2bc-2c(φ(ξ))2),ξ=x-ct,

(5)

其中函数φ=φ(ξ)可根据b的符号由文献[13]的表1～表3中分别选取, 从而可写出式(5)的具体解析表达式, 为简洁, 本文省略其列举过程. 此外, 文献[2-3]中未给出行波解(5).

1.3 Liouville方程的约化变换方程和精确解

由表2中子李代数span{X2+cX1}对应的约化方程可得

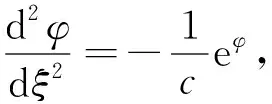
(6)

在方程(6)两边同时乘以φ′得

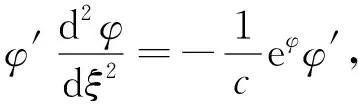
(7)

对方程(7)两边同时关于ξ积分一次, 并记积分常数为κ, 可得

进一步得

令变换φ=lnψ(ξ), 于是该方程可写为

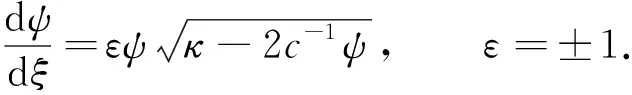
(8)

用分离变量法可求出方程(8)的精确解, 从而可得方程(1)的行波解, 结果列于表3. 文献[2-3]未给出表3中方程(1)的行波解.

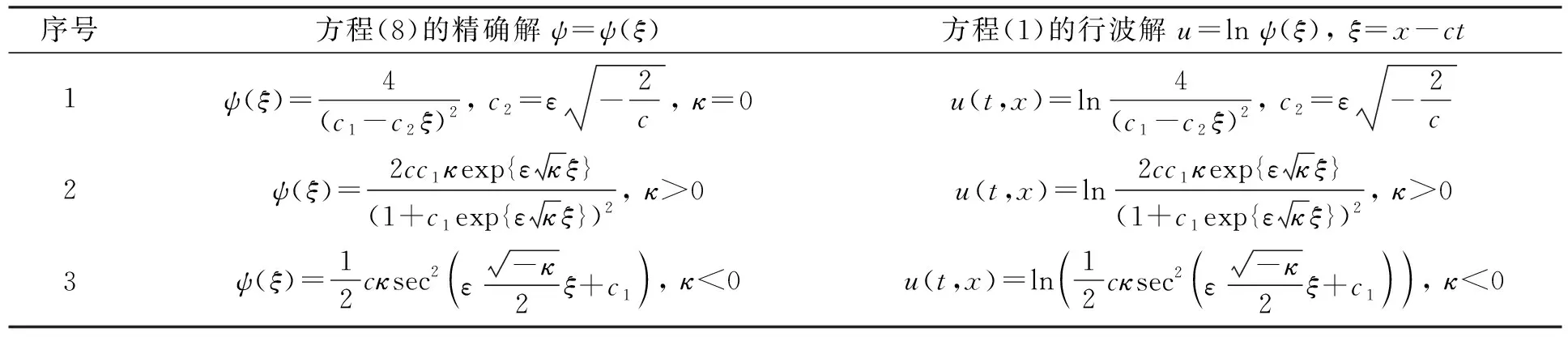
表3 方程(1)和方程(8)的显式精确解Table 3 Explicit exact solutions of equation (1) and equation (8)

2 ψ(ξ)展式法的基本思想和求解步骤

许多非线性偏微分方程不能采用广义tanh函数法得到其精确解, 例如, Rosenau方程ut+uxxxxt+ux+uux-αuxx=0(0≤α≤1)很难找到精确解. 因此, 为寻找非线性偏微分方程的更多精确求解方法与技巧, 本文借助Liouville方程的约化变换方程(8)及其精确解给出ψ(ξ)展式法的主要求解步骤. 考虑一般形式的非线性演化偏微分方程

G(u,ut,ux,utt,uxx,uxt,…)=0,

(9)

其中:u=u(t,x)是未知函数;G是关于u及其各阶偏导数的多项式, 并包含非线性项和最高阶导数项.

ψ(ξ)展式法的主要求解步骤如下：

1) 做行波变换ξ=x-ct, 其中c为常数, 表示波速. 若假设方程(9)具有形如u(t,x)=V(ξ)的行波解, 则方程(9)可约化变形为常微分方程

G(V,-cV′,V′,c2V″,V″,-cV″,…)=0.

(10)

2) 若可能, 先对方程(10)两边同时关于ξ积分一次或多次, 取积分常数为零, 再假设方程(10)的解析解为

V(ξ)=d0+d1ψ(ξ)+…+dn(ψ(ξ))n,

(11)

其中ψ=ψ(ξ)满足方程(8), 其具体表达式可根据κ的符号由表3中分别选取. 一般地, 正整数n可采用齐次平衡原理[5-7], 并通过平衡方程(10)中的非线性项和最高阶导数项得到, 其中di(i=0,1,…,n)为待定实参数.

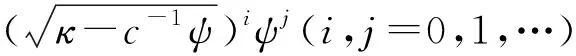
4) 用吴消元法[12]并结合软件Reduce计算, 将求出的常数di(i=0,1,…,n),κ,c代入方程(11), 从而可写出方程(9)的行波解, 其中函数ψ=ψ(ξ)可根据κ的符号由表3中分别选取.

3 变换方程(8)的精确解及ψ(ξ)展式法的应用

3.1 Kawahara方程的新行波解

考虑Kawahara方程[14]

ut+uux+αuxxx+βuxxxxx=0,

(12)

其中α,β为常数. 文献[14-15]给出了方程(12)的相关应用; 文献[3,16-17]给出了方程(12)的sech4-型孤波解. 做行波变换ξ=x-ct, 其中c为常数, 表示波速, 且假设u(t,x)=V(ξ)为方程(12)的解, 因此方程(12)可约化为常微分方程

βV(5)+αV‴+VV′-cV′=0.

(13)

对方程(13)两边同时关于变量ξ积分一次, 并取积分常数为零, 可得

2βV(4)+2αV″+V2-2cV=0.

(14)

根据ψ(ξ)展式法式(11)和齐次平衡原理, 以及平衡方程(13)中V(5)与VV′项或方程(14)中V(4)与V2项, 可得n=2, 于是可假设方程(13)或方程(14)解析解的表达式为

V(ξ)=d0+d1ψ(ξ)+d2(ψ(ξ))2,

(15)

其中di(i=0,1,2)为待定常数, 函数ψ=ψ(ξ)满足方程(8). 将式(15)代入方程(13), 并反复利用方程(8)再结合软件Reduce计算整理, 可得

用吴消元法并结合软件Reduce计算可得该方程组的一组解为

同理, 用ψ(ξ)展式法将式(15)代入方程(14)可得

因此, 方程(12)的行波解为

(16)

(17)

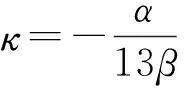
3.2 Kadomtsev-Petviashvili方程的新行波解

(3+1)维Kadomtsev-Petviashvili(KP)方程[19]

utx+6(uux)x+uxxxx+3εuyy+3εuzz=0,ε=±1,

(18)

在描述弱色散介质、 流体动力学和等离子体物理学中的三维孤子, 弱非线性恢复力的长波长水波, 铁磁介质中的波等方面应用广泛. 文献[4,20-22]讨论了方程(18)的精确解法及可能的应用前景.

做行波变换, 令ξ=x-ct+ky+λz, 其中c,k,λ均为常数, 且假设u(t,x,y,z)=V(ξ)为方程(18)的解, 则方程(18)可约化为常微分方程

V(4)+(3εk2+3ελ2-c)V″+6V′2+6VV″=0.

(19)

用ψ(ξ)展式法式(11)并结合齐次平衡原理, 平衡方程(19)中V(4)和VV″项可得n=1, 因此方程(19)解析解的表达式可假设为

V(ξ)=q0+q1ψ(ξ),

(20)

其中q0,q1为待定常数, 函数ψ=ψ(ξ)满足方程(8). 将式(20)代入方程(19), 并反复用方程(8)再结合软件Reduce计算可得关于ψ的多项式, 分别令ψi(i=1,2,3)的各项系数为零, 可得关于q0,q1,c,k,λ,κ的代数方程组

(21)

其中函数ψ=ψ(ξ)可根据κ的符号由表3中分别选取. 从而可写出行波解(21)的下列表达式：

其中ε=±1,c,c1,κ,k,λ为常数. 文献[4,20-22]中未给出显式行波解ui(t,x,y,z)(i=1,2,3). 不同类型行波解u3(t,x,y,z)的空间和投影图像分别如图1和图2所示.

图1 当ε=-1, c=5, c1=-0.01, κ=-1, k=-1, λ=0.01, z=0时, u3(t,x,y,z)的空间图像Fig.1 Spatial graphs of u3(t,x,y,z) when ε=-1, c=5, c1=-0.01, κ=-1, k=-1, λ=0.01, z=0

图2 当ε=-1, c=3, c1=-0.01, κ=-1, t=2, λ=0.01, z=0时, u3(t,x,y,z)的空间图像Fig.2 Spatial graphs of u3(t,x,y,z) when ε=-1, c=3, c1=-0.01, κ=-1, t=2, λ=0.01, z=0

利用这些图像可直观讨论自由参数及其相互间的作用对行波解的动力学行为、 波的传播和波的结构特征的影响. 图1为当波速c=5, 参数z=0,ε=-1,c1=-0.01,κ=-1,k=-1,λ=0.01时, 在3个不同时刻t=3,5,7, 行波解u3(t,x,y,z)在空间呈现的不同冲击波特征. 图2为当波速c=3, 参数z=0,ε=-1,c1=-0.01,κ=-1,λ=0.01, 且自由变量y的系数取不同值k=2,-2,-0.01时, 行波解u3(t,x,y,z)在空间呈现的不同奇异波和冲击波特征.

综上, 本文用Liouville方程的约化变换方程及精确解构造了一种求解非线性偏微分方程精确解的ψ(ξ)展式法, 并利用该方法讨论了Kawahara方程和(3+1)维Kadomtsev-Petviashvili方程, 得到了一些新的行波解.