无刷直流电机同步的电路设计

李 慧，储汇连，赵启亮，刘 越

(长春工业大学 电气与电子工程学院，长春 130012)

近年来，无刷直流电机(BLDCM)的稳定运行已引起人们广泛关注, 该类电机在某些特定参数条件下会产生混沌现象[1]，因其非周期和不可预测性[2-3]，被认为是错误或故障而误处理，导致电机损毁，进而影响整个工程的运行. 为避免混沌发生，研究人员提出了有效控制策略，如滑模控制法[4]、 反馈控制法[5]和自适应模糊控制法[6]，从而实现了该类系统的同步算法研究与控制[7-9]. 但上述方法主要基于理论仿真，且控制器的设计较复杂，在实际工程中不易实现.

本文提出反推同步控制方法，实现2个BLDCM的同步控制，从而实现驱动系统与响应系统的同步运行. 首先，基于BLDCM负载运行状态下的数学模型，分析该系统的混沌动力特性; 其次，基于Lyapunov稳定性原理，设计反推同步控制器并进行稳定性研究; 最后，设计基于电流转换器的BLDCM电路仿真器. 数值仿真及电路实现表明，该控制器的设计参数较少，在2～4 s即可实现快速稳定同步，且能保证系统的稳定性.

1 BLDCM模型及混沌特性

d-q坐标下的BLDCM数学模型[10]为

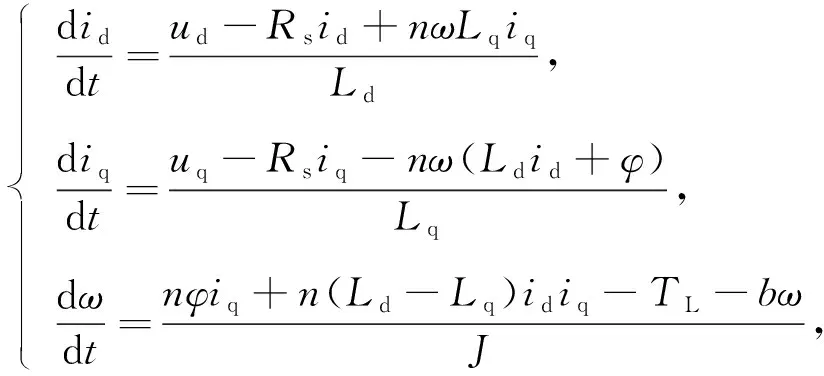
(1)

其中，id和iq分别为直轴和交轴定子电流，ud和uq分别为直轴和交轴定子电压，TL为外部扭矩，φ为转子永磁磁链，Rs为定子电阻，n为极对数，J为转动惯量，b为阻尼系数. 假设电机系统气隙均匀，并对系统进行线性映射与时间尺度变换[10]可得

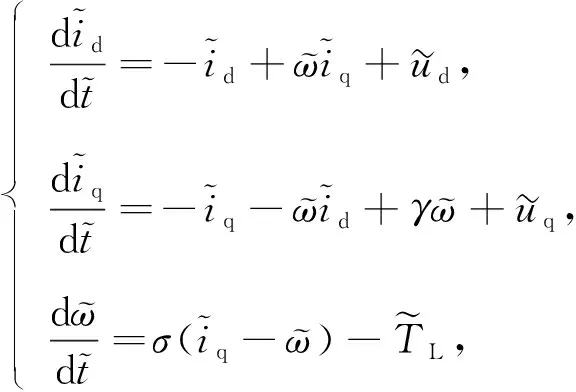
(2)

其中，γ为自由参数，σ=bτ/J为系统参数.

图1 的相轨迹曲线Fig.1 Phase trajectories of

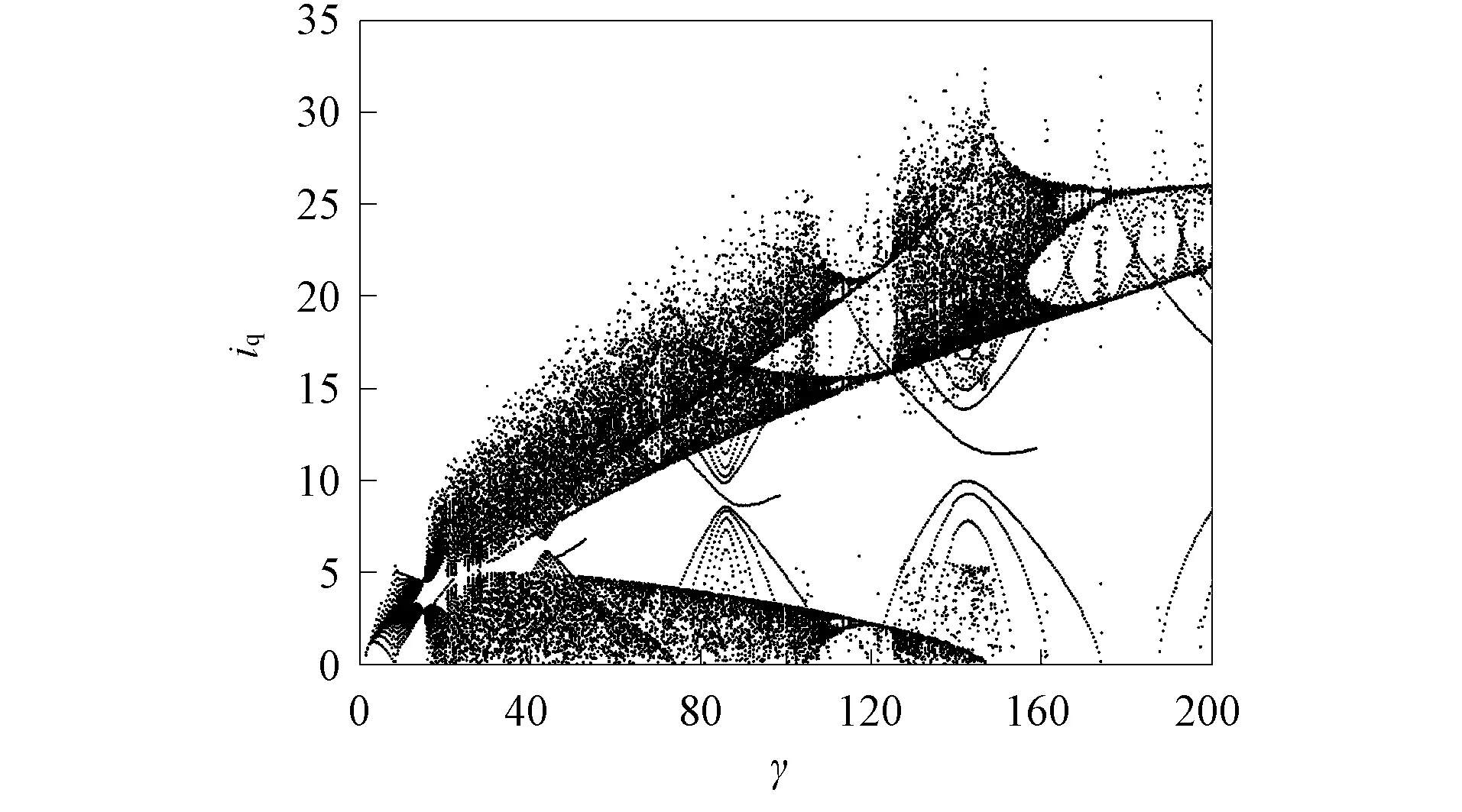
图2 Hopf分岔图Fig.2 Hopf bifurcation diagram

2 反推同步算法

2.1 反推同步控制器的设计

本文设计了反推同步控制器实现混沌系统同步，具体过程如下.

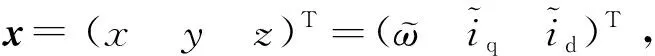
(3)

响应系统为

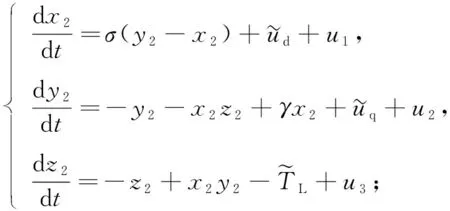
(4)

误差方程为

(5)

对误差方程求导可得

(6)

为保证驱动系统(3)和响应系统(4)实现同步控制，设计控制器方程为

(7)

2.2 系统的稳定性

当电机负载运行时，若控制器满足方程(7)，则驱动系统(3)和响应系统(4)全局一致渐近稳定且误差渐近趋于零.

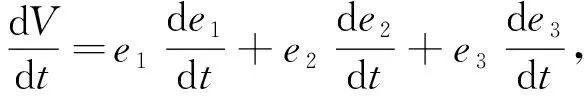
(8)

将式(6)代入式(8)可得

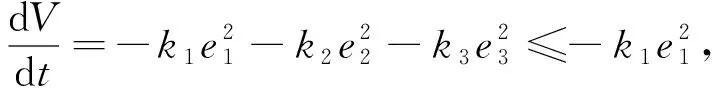
(9)

因此

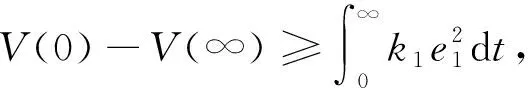
(10)

即V有界，系统全局一致渐近稳定.

由于V有界，根据Barbalat推论可得

即系统误差渐近趋于零. 因此，驱动系统(3)和响应系统(4)可实现同步.

3 仿真分析及电路实现

3.1 仿真分析

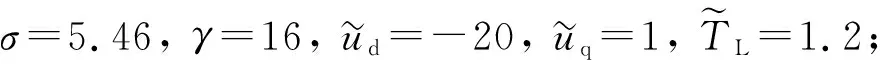
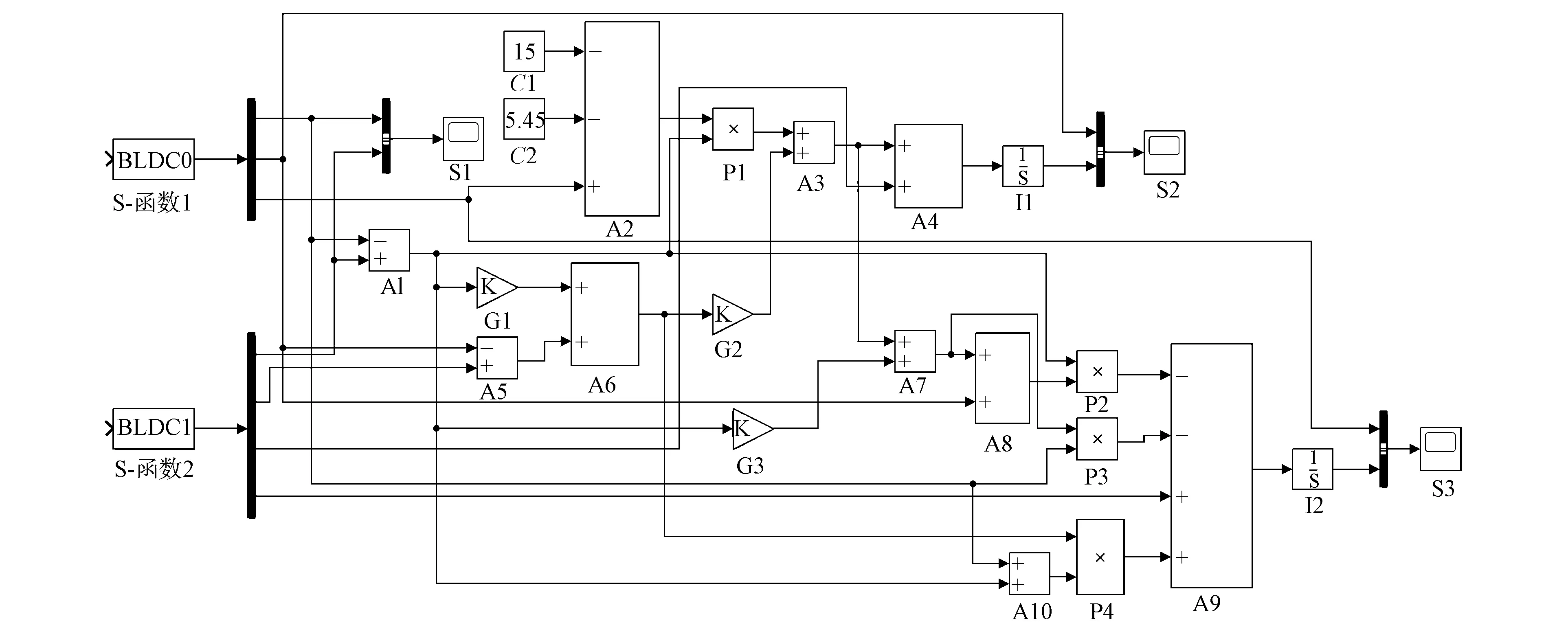
图3 BLDCM混沌同步仿真模型Fig.3 Model of BLDCM chaotic synchronization simulation

图4 (x1,x2)，(y1,y2) 和(z1，z2)随时间t的变化曲线Fig.4 Cureves of (x1,x2)，(y1,y2) and (z1,z2) with time t

图3中的S-函数1表示驱动系统，S-函数2表示响应系统，A1～A10表示加法器，S1～S3表示示波器，G1～G3表示增益，C1和C2为2个常数，P1～P4为乘法器，I1和I2为2个积分器.

由于驱动系统(3)和响应系统(4)的初始条件不同，因此初始状态运行轨迹不同步. 由图4可见，3个状态变量均在2～4 s即可实现快速稳定同步，响应速度较快. 该反推控制器设计简单，可使BLDCM实现快速同步，并保证系统稳定运行.

3.2 电路实现

电路仿真平台的搭建主要以电压模式电路为主[12-13]，存在如下问题: 1) 产生的信号频谱范围较窄，在实际工程中不易实现； 2) 当处理大信号时，输出电压信号的转换速率较低； 3) 在高集成电路设计过程中，采用高功耗、 小尺寸元件会使器件的内部电场增强，影响器件正常工作. 基于CCCⅡ设计的仿真器可解决上述问题，且设计简单，易实现. 因此，采用CCCⅡ搭建BLDCM电路仿真平台，观察混沌与同步现象，具有快速、 宽频、 低功耗和低电压等特点.

根据驱动系统(3)和响应系统(4)，选取运算放大器AD844和四象限乘法器/除法器AD734AN为关键器件. 设其他参数值为

C1=C2=C3=10 nF，

R1=R4=R8=R12=1 kΩ，

R2=R3=R5=R10=R19=100 kΩ，

R6=R11=R17=R18=10 kΩ，

R7=100.1 kΩ，R13=4.672 kΩ，R14=0.25 kΩ，

R15=R16=2.5 kΩ，R9=0.2 kΩ.

为验证理论分析及数值仿真结果，利用Multisim平台设计仿真器电路，如图5所示. 其仿真结果如图6所示. 由图6可见，驱动系统(3)和响应系统(4)可实现同步，电路仿真与数值仿真结果一致，因此该同步电路设计正确.

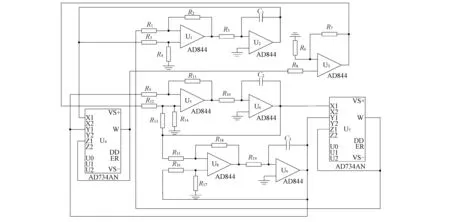
图5 BLDCM混沌系统同步电路Fig.5 Synchronous circuit of BLDCM chaotic system

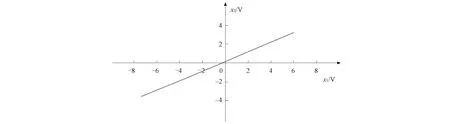
图6 x1和x2的同步电路仿真结果Fig.6 Results of synchronous circuit simulation for x1 and x2

综上，本文从相位图、 分岔图和Lyapunov指数分析了BLDCM的混沌动力特性，并基于Lyapunov稳定性原理设计了反推同步控制器. 通过数值分析与仿真器电路实现，验证了该方法在2～4 s即可快速稳定地实现混沌系统的同步跟踪. 由于反推同步控制器的调整参数较少，设计简便，且状态变量由系统获得，因此在工程上易实现.