二维函数光子晶体波导带隙和电场分布的调制

刘晓静，张晓茹，任明丽，潘 庆，杨涪铨，刘 晗，孟祥东，郭义庆

(1. 吉林师范大学 物理学院，吉林 四平 136000； 2. 北京师范大学 物理学院，北京 100875;3. 中国科学院 高能物理研究所，北京 100049)

光子晶体由两种及两种以上不同材料周期排列构成[1-2]，具有光子带隙、 光局域化和缺陷态等特性[3-7]，可制作半导体激光器、 波导、 光学滤波器、 发光二极管、 光学放大器和光学衰减器[8-11]等光学器件. 波导[12]具有灵敏度高、 集成度高、 非破坏性等特点，可用于传感器等光学器件中[13-16]. 文献[17-19]研究了光子晶体波导定向耦合及多模干涉效应的光分束器; 文献[20-29]研究了二维函数光子晶体的带隙结构、 Dirac点分布及含点缺陷的光场分布. 二维函数光子晶体异于常规光子晶体，其介质柱的介电常数可表示为空间坐标函数. 由于二维函数光子晶体介质柱的介电常数具有可调节性，因此可不更换介质柱，通过调节介质柱介电常数的参数，实现二维函数光子晶体的带隙结构和电场分布可调，得到具有异于常规光子晶体独特性质的晶体.

本文研究二维函数光子晶体波导的带隙结构和电场分布. 当二维函数光子晶体波导中不含点缺陷时，通过改变波导中介质柱介电常数的参数k和b值，可调节波导的禁带数目、 禁带位置及缺陷模的数目和位置. 当二维函数光子晶体波导中所含介电常数为函数的点缺陷时，通过改变点缺陷介质柱介电常数的参数k和b值，调节光在波导中的传播方向和电场分布.

1 理论分析

文献[20-21]给出了二维函数光子晶体介电常数的Fourier变换，介质柱的介电常数为

(1)

或

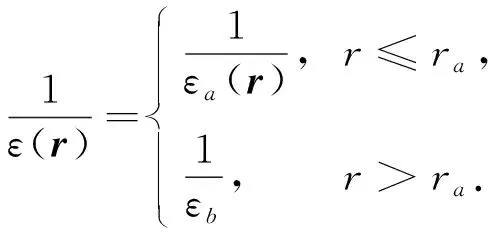
(2)

方程(2)可写为

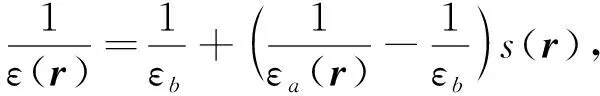
(3)

其中

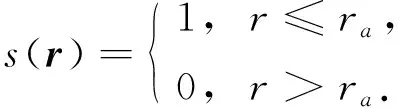
(4)

1/εa(r)的Fourier变换可写为

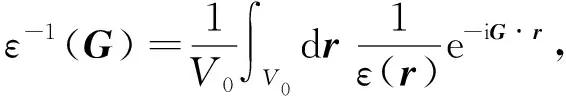
(5)

在二维倒易空间中为

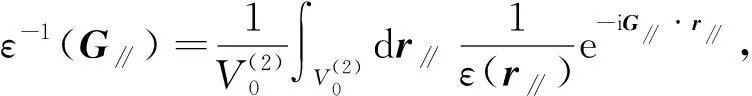
(6)

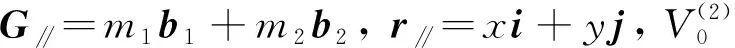
将方程(3)代入方程(6)可得

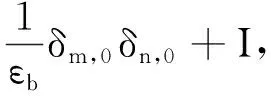
(7)

其中

I1-I2,

(8)

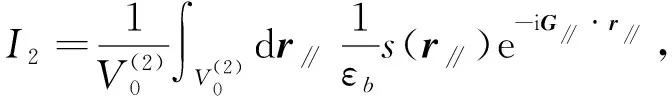
(9)

从而有

|r∥|=r∥=r， |G∥|=G∥, dr∥=ds=rdrdθ，

θ为r∥和G∥的夹角. 通过计算可得

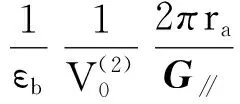
(10)

当G∥→0(m→0，n→0)时，

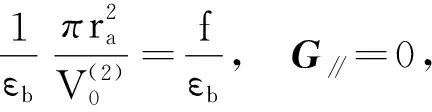
(11)

在方程(12)中，考虑εa(r，θ)=εa(r)，当G∥=0时，

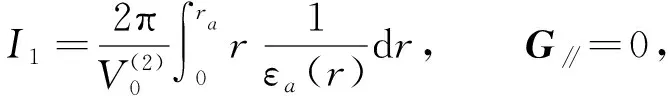
(13)

将I1，I2和I代入方程(7)可得

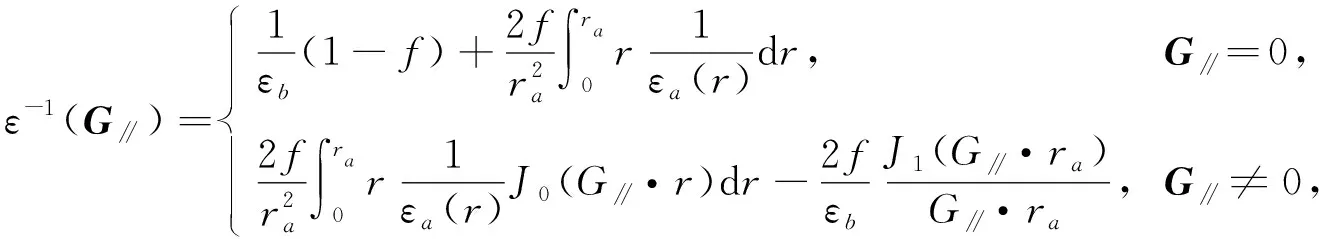
(14)

其中εa(r)=εa. 若εa为常数，则方程(14)可写为

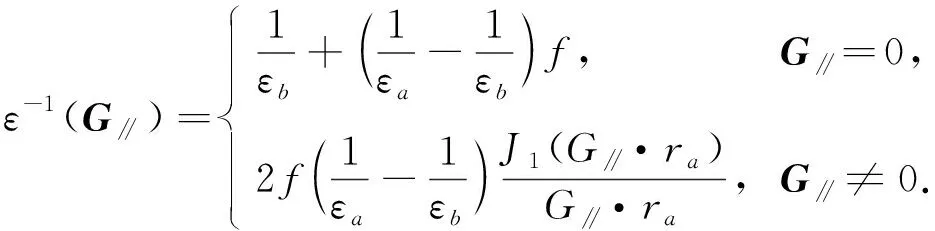
(15)

方程(15)是二维常规光子晶体介电常数的Fourier变换, 即二维常规光子晶体是二维函数光子晶体的一种特殊情况. 通过平面波展开法，给出横电(TE)波的特征方程为

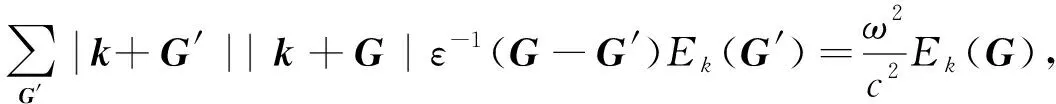
(16)

将方程(14)代入(16)，可得二维函数光子晶体的带隙结构.

在二维函数光子晶体中，引入一条线缺陷形成二维函数光子晶体波导. 在一阶电光效应中，介质柱介电常数函数形式为

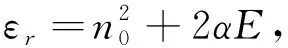
(17)

当外加电场为沿介质柱半径r线性分布的函数

E=E0r+d

(18)

时，通过Faraday电磁感应定律可得该电场分布形式[24]. 介电常数可写为

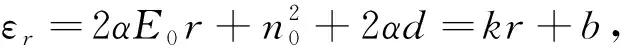
(19)

2 数值分析

根据式(14)～(19)以及COMSOL 仿真软件，通过计算和模拟可得二维函数光晶体波导的电场分布和带隙结构.

本文以空气为背景，研究正方形结构的二维函数光子晶体波导，结果如图1所示，其中白色圆圈为波导介质柱，黑色圆圈为波导中引入的点缺陷介质柱，介质柱均位于空气背景中，柱子的轴心沿z轴方向. 介质柱介电常数的函数形式为εr=kr+b(0≤r≤ra)，其中，函数系数k=7.8×107m-1，参数b=15，介质柱半径ra=0.28a，晶格常数a=10-7m，波导间距d=2a.

选择图1虚线框内的1×8超元胞，在TE波偏振下，得到二维函数光子晶体波导的带隙结构，如图2(A)所示，其中横坐标表示波矢K(2π/a)，纵坐标为归一化频率(ωa/(2πc)). 由图2(A)可见，当ω=0～0.6时，出现两条禁带，禁带的频率分别为 0.38～0.52 和 0.22～0.298. 在第一条禁带中出现一条缺陷模，即图中黑色实线. 在缺陷模上选择一点A(用圆圈圈出)，其归一化频率为ω=0.460 6. 图2(B)为本征场分布. 由图2(B)可见，在波导中间的线缺陷处，存在一个局域电场，且强度较强.

图1 二维函数光子晶体波导的结构Fig.1 Structure of two-dimensional functional photonic crystal waveguide

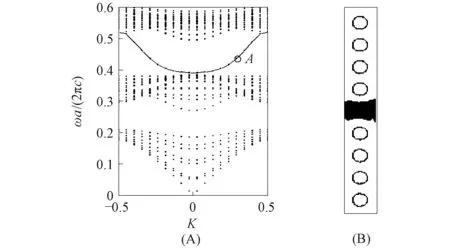
图2 二维函数光子晶体波导的带隙结构(A)和A点对应的本征场(B) Fig.2 Band gap structure of two-dimensional functional optical crystal waveguide (A) and corresponding eigenfield of point A (B)

下面研究在二维函数光子晶体波导中不加点缺陷时，周围介质柱介电常数的函数系数k和参数b对带隙结构的影响. 首先研究函数系数k对带隙结构的影响. 设参数b=15，函数系数k=7.8×107，30.8×107，50.8×107m-1，对应的带隙结构分别如图3(A)～(C)所示. 由图3(A)可见，带隙中出现两条禁带，其频率分别为 0.385～0.49 和 0.21～0.27，其中在 0.385～0.49 内出现一条缺陷模； 由图3(B)可见，带隙中出现3条禁带，频率分别为 0.54～0.6，0.348～0.451 和 0.19～0.25，其中在 0.54～0.6 和0.348～0.451 内分别出现一条缺陷模； 由图3(C)可见，带隙中出现3条禁带，其频率分别为0.49～0.585，0.306～0.421 和 0.17～0.23，其中在 0.49～0.585 和 0.306～0.421 内分别出现一条缺陷模. 因此，当k值增加时，二维函数光子晶体波导带隙结构中禁带的数目增加，禁带红移，缺陷模的数目增加，且缺陷模频率范围减小. 所以改变函数系数k，可调节二维函数光子晶体波导的带隙结构.

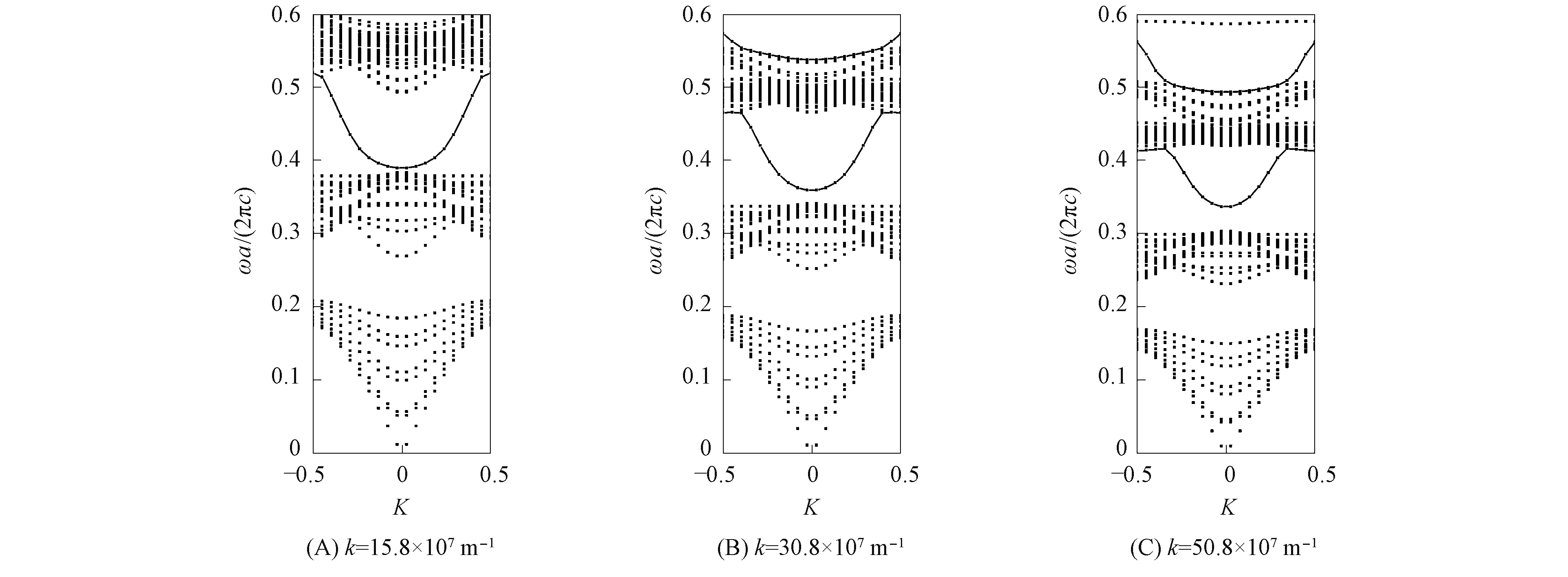
图3 当参数b相同时，函数系数k对二维函数光子晶体波导带隙结构的影响Fig.3 Effects of functional coefficients k on band gap structure of two-dimensional functional photonic crystal waveguide when parameters b are same

其次研究参数b对带隙结构的影响. 设函数系数k=7.8×107m-1，参数b=9，15，21，对应的带隙结构分别如图4(A)～(C)所示. 由图4(A)可见，带隙中出现两条禁带，频率分别为 0.475～0.575 和 0.26～0.30，其中在 0.475～0.575 内出现一条缺陷模； 由图4(B)可见，带隙中出现两条禁带，频率分别为 0.38～0.48 和 0.2～0.27，其中在 0.38～0.48 内出现一条缺陷模； 由图4(C)可见，带隙中出现3条禁带，频率分别为 0.51～0.60，0.34～0.51和 0.175～0.24，其中在 0.51～0.60 和 0.34～0.51 内分别出现一条缺陷模. 因此，当b增大时，二维函数光子晶体波导带隙结构中禁带的数目增加，禁带红移，缺陷模的数目增加，且缺陷模频率范围减小. 所以改变参数b也可调节二维函数光子晶体波导的带隙结构.

图4 当函数系数k相同时，参数b对二维函数光子晶体波导带隙结构的影Fig.4 Effects of parameters b on band gap structure of two-dimensional functional photonic crystal waveguide when functional coefficients k are same

当归一化频率ω=0.460 6时，将一个点缺陷加入二维函数光子晶体波导中，研究其介质柱介电常数参数对电场分布的影响. 首先，研究点缺陷介质柱介电常数中参数b对二维函数光子晶体波导电场分布的影响. 设周围介质柱介电常数函数形式为εr=7.8×107r+15，半径ra=0.28a； 点缺陷函数系数k=7.8×107m-1，点缺陷介质柱半径为ra=0.25a，参数b=6，8，10，20，对应的电场分布分别如图5(A)～(D)所示，其中白色五角星表示线源，其位于波导左侧，点缺陷介质柱位于波导中心处. 由图5(A)可见，当参数b=6时，水平和竖直方向均有电场分布，此时光沿水平和竖直两个方向传播； 由图5(B)可见，当参数b=8时，竖直方向电场消失，水平方向有明显的电场分布，此时光主要沿水平方向传播； 由图5(C)可见，当参数b=10时，水平和竖直方向的电场被截止，此时在水平和竖直方向仅通过较微弱的光； 由图5(D)可见，当参数b=20时，水平方向电场消失，竖直方向有明显的电场分布，此时光主要沿竖直方向传播.

图5 当加入点缺陷且函数系数 k相同时，参数b对二维函数光子晶体波导中电场分布的影响Fig.5 Effects of parameters b on electric field distribution of two-dimensional functional photonic crystal waveguide when point defect is added and functional coefficients k are same

其次，研究点缺陷介质柱介电常数中函数系数k对二维函数光子晶体波导电场分布的影响. 设参数b=10，半径为ra=0.25a，函数系数k=2.8×107，7.8×107，-18.8×107，35.8×107m-1，对应的电场分布分别如图6(A)～(D)所示. 由图6(A)可见，当函数系数k=2.8×107m-1时，仅水平方向的电场分布较明显，即光沿水平方向传播； 由图6(B)可见，当函数系数k=7.8×107m-1时，水平和竖直方向均无电场分布，此时在两个方向仅通过微弱的光； 由图6(C)可见，当函数系数k=-18.8×107m-1时，水平和竖直方向均存在电场，即光沿竖直和水平方向传播； 由图6(D)可见，当函数系数k=35.8×107m-1时，水平方向电场消失，竖直方向有明显的电场分布，此时光主要沿竖直方向传播. 因此改变点缺陷介质柱函数系数k也可控制光在波导中的传播方向和电场分布.

图6 当加入点缺陷且参数b相同时，函数系数k对二维函数光子晶体波导中电场分布的影响Fig.6 Effects of functional coefficients k on electric field distribution of two-dimensional functional photonic crystal waveguide when point defect is added and parameters b are same

综上，本文给出了二维函数光子晶体波导的Fourier形式，并用COMSOL仿真软件计算和模拟了其电场分布和带隙结构. 结果表明： 当二维函数光子晶体波导中不含点缺陷，波导中介质柱介电常数参数b和k的值分别增加时，二维函数光子晶体波导带隙结构中禁带的数目增加，禁带红移，缺陷模的数目增加，且缺陷模频率范围减小； 当二维函数光子晶体波导中含介电常数为函数的点缺陷时，改变点缺陷介质柱参数k和b的值，可改变二维函数光子晶体波导中的电场分布，并控制光的传播方向，具有光学开关的作用. 因此，通过改变外加电场即可调节其带隙结构、 光的传播方向和光场分布，即二维函数光子晶体波导具有调制功能.