有限域上基于拉格朗日插值多项式渐进图像传输

刘易麟

（中国石油天然气股份有限公司四川销售分公司科研设计所，成都 610000）

0 引言

通过一个低速信道传输高分辨率图片或者视频，例如电话线，通常遇到的是长时间交互的问题。因此，对认知图片内容有高需求的用户，甚至在一个早的阶段就中止传输过程[1]。渐进图像传输就是一个可以解决上述问题的技术。

通常来说，我们定义渐进式图像传输是一种在接收设备上通过远程传输逐渐显示近似图像技术。一种长时间等待高清图片替代方式，远程用户可以迅速地掌握一个粗略的图像，然后，不停地，图片将会一点一点地清晰起来。因此，对于远程用户，尤其是在低速网络通道上管理大量图像，这是重要且实用的。最近几年，有许多渐进图像传输方法发表发明。这些方法中大部分使用的离散小波变换技术，将图像分成一个较为重要的部分和许多不是很重要的部分，然后首先传输较为重要的部分到目标[6-9]。另外，也有许多渐进图像传输方法使用的其他的技术。如：基于分水岭的方法，Caron和Rivest也发表了用于渐进图像传输的分割编码方法[3]。在1997年，Chang提出了一种基于主成分分析的有效渐进图像传输方法[2]。后来，Jordan提出了用于二进制的渐进图像传输的多边形近似算法[4]。在2001年，Chung和Tseng发表了另一种基于四叉树和具有分辨率控制的阴影处理的渐进图像传输方法[5]。

然而，这些方法大部分是针对黑白图像，通常两部分是能够恢复原始图片的最小信息，换句话说，用户不能确定原始图片最小信息的最少片段数量。本文提出一个新的基于拉格朗日插值多项式的渐进图像传输方法。通过这个新的方法，我们可以通过任何的渐进形式传输图像，可以通过设置任意的最小的片段得到大致的信息，还有，因为它是基于拉格朗日插值多项式的特征，所以从信息安全的各个角度来看这是一个安全的方法。另外，这个新的方法可以轻松的扩展到音频和视频领域。

1 理论基础

在这个方法中，我们使用了有限域上的拉格朗日插值多项式从而把原始图像分割成N个片段然后通过接收N个片段的部分恢复原始图像。因此，一些关于有限域上的拉格朗日插值多项式信息需要简要的说明。

拉格朗日插值多项式P（x）是多项式的复杂度≤（n-1）通过 n 个点（（x1，y1=f（x1）），（x2，y2=f（x2））…，（xn，yn=f（xn））），然后由得到下式：

对于n=3个点：

请注意，函数P（x）通过特定的点（xi，yi），可以看出n=3如下：

推广到任意的n：

通过上述的公式，如果这里有n+1个点（（x1，f（x1）），（x2，f（x2））…，（xn+1，f（xn+1）））以及xi≠xj，（1≤i，j≤n+1），一个独一无二n阶的多项式可能被确定[10-11]。我们需要解释的是所有的计算针对数字图像，所以所有的系数和结果在上述的方程式中应该是相同有限域的元素。

静态的图像Z被看作是在平面域中一个二进制连续函数：Z=f（x，y），0≤x≤m，0≤y≤n。在定律中，对于图像Z，m和n分别意味着宽和高，（x，y）是图像中任意的点坐标，f（x，y）是点的像素值。图像数字化后，矩阵中行和列的位置Z=f（x，y）是相对图像坐标中每个点的位置对应。元素的值相当于像素的值，另外在f（x，y）中参数 x和 y需要满足条件 0≤x≤m，0≤y≤n，其中 m和n均为整数。下面的等式意味：f（x，y）=Zx，y其中Zx，y表示xth行和yth列的像素值。

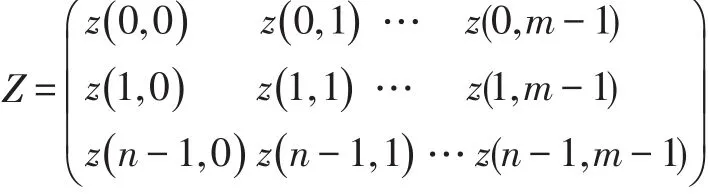
所有的像素值在任何的数字图像中都是有限整数，作为一个彩色图像，f（x，y）∈[0，224）；作为一个原始的256阶灰度图像，像素值对应了它的灰度值，当然灰度值也是有限的，f（x，y）∈[0，28），所以，任何关于图像的计算需要被限定于一个有限域中。即任何关于数字图像的计算结果必在这些图像的像素值相同的有限域中。

有限域也称为伽罗华域，是代数的基本话题。有限域GF（n）是一组在加法和乘法封闭的n个元素，对其中每个元素都有一个加法和乘法逆（除了对0元素没有乘法逆）[12]。例如，有限域 GF（2）可以被表达在｛0，1｝上的加法和乘法都模2的操作（即加法是“或”，乘法是位之间的“与”操作）。类似的，如果n是一个素数，那么我们可以表示有限域GF（n）为集合{0，1，…，n-1}，在其上的加法和乘法同样执行模n。然而，假设n＞1不是素数，那么{0，1，…，n-1}使得加法和乘法都执行模n不是一个有限域。例如，n为4时，有限域{0，1，2，3}关于加法和乘法模4是封闭的，然而，元素2已经没有逆乘法。因此，我们不能使用加法和乘法模2w来执行w＞1的二进制字编码。不管怎样，由于数字信号的特点，有限域GF（2w）正是所需要的。为了构造有限域GF（2w），我们使用参考文献附录A中的方法[13]。

2 提出方法

在这节，详细介绍一种新的基于拉格朗日插值多项式的渐进图像传输方法。

关于这种方法所有步骤的细节描述如下所示：

步骤1：根据需要逐步传输图像的类型确定的有限域。

假设2w位可以表达图片像素的任何值，然后我们表示有限域为GF（2w），从0到2w-1每个整数可以用GF（2w）中的一个元素唯一地表示。例如，在二进制图像中每个像素值被定义为0或者1，因此，计算域为有限域GF（21）。由于同样的原因，当图像为256阶灰度图像或者彩色图像时，计算域应该为GF（28）及GF（224）。

步骤2：识别由原始图像划分出来的N个片段的数量。

我们把原始图片划分为N个小信息部分，N可根据应用环境或者实际需求来确定。

步骤3：确定最小数MIN，通过对MIN最少片段计算，我们能获得原始图像的一些信息。

步骤4：确定最大数MAX，我们能完整地恢复原始图像（MAX≤N）。然而，这一步不是必须的，如果我们不选择MAX的值，这个数字等于N。

步骤5：根据下述公式获得V的值：

步骤6：通过原始图像有序地获得V像素，将这些像素排列成列，并将每个像素值表示为二进制格式，得到一个二进制矩阵，我们将它标记为A。所有的处理如图1所示。

图1

步骤7：创建一个矩阵A具有相同大小的新矩阵A’，A’中每一个元素可以通过下述的公式得到：

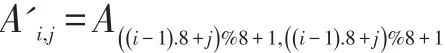
然后，我们可以根据下述公式从矩阵A’获得一个集合S：

步骤8：划分集合S为（MAX-MIN+1）个子集，第i个子集有集合S中的MIN+i-1个元素，我们表示第i子集 SUBi。

步骤 9：制作 SUBi多项式系数，（MAX-MIN+1）不同多项式fi（x）可以被定义。然后，我们通过令x={1，2，…，N}计算每一个多项式获得N值。然后把每一个Mi的值放入第i个片段。

步骤10：重复第9步直到原始图像的所有像素都被计算。

通过以上这些步骤我们可以把原始图像分割为N个片段。根据第1节拉格朗日插值多项式公式的描述，如果接收端接收多于最小的片段，我们可以获得一些关于原始图像的信息；如果接收最大片段或者更多，我们可以获得无损的原始图像。

3 实验结果

在第2节已经介绍了我们提出的可用于任何类型的图像处理方法。这一节竟会列出2个典型灰度图和彩色图的例子，以说明这个新的渐进图像传输方法的效果。

例1：

在图2中图像（a）是一个我们想通过渐进传输的原始图像，并且这是一个256阶灰度图。首先，根据原始图像的类型，我们设定有限域GF（28）来执行计算。然后我们确定其它的参数如下：MIN=3、MAX=5和V=12。接下来，根据步骤6到10的描述，我们把原始图像分为 5个部分。图像（b），图像（c）和图像（d）分别是在接收端由3个、4个和5个部分重建的图像。这里我们需要说明的是在图2中图像（d）等同于图像（a）。

图2 灰度图

例2：

图像（a）是一个原始的彩色像，如图3所示。我们设定有限域GF（224）来执行计算，其他参数值与例1相同。然后执行第2节中步骤6到步骤10的操作，我们仍然把原始图像分为5个部分。图像（b），图像（c）和图像（d）分别是在接收端由3个、4个和5个部分重建的图像，图像（d）等同于图像（a）。

图3 彩色图

4 结语

本文提出了一个新的渐进图像传输方法，这个方法是基于在有限域上的拉格朗日插值多项式。新的方法可以应用于所有的图像类型，获得原始图像信息的最少部分数量可根据实际需要来确定。由于上述所有特征，本方法是一种优秀的渐进图像传输方法。另外，这种新的方法可以轻易地扩展到音频和视频领域，所以，我们认为这个方法将会有一个很好的前景。