基于谷歌计算思维课程的中学生计算思维培养策略

赵福生，刘力

（沈阳师范大学教师教育学院，沈阳 110034）

0 引言

形式化是指分析、研究思维形式结构的方法。它把各种具有不同内容的思维形式（主要是命题和推理）加以比较，找出其中各个部分相互联结的方式[1]。现实中的问题可以抽象为一个数学问题或一个形式化问题[2]。计算思维作为核心素养在教育部《普通高中信息技术课程标准（2017年版）》提出后，引起了普遍重视，继理论探讨之后，计算思维的实践应用成为一个热点。作为计算思维培养主要阵地的“算法与程序实现”部分，实施效果难以令人满意。因此，本研究采用内容分析法分析谷歌计算思维课程并与国内课程内容进行对比，认为计算思维培养的策略应以数学类问题为引入，以数学+形式化问题为过渡，以形式化问题为重点，结合恰当的教学设计，才能达到发展学生计算思维的目的。

1 培养计算思维的六类问题

2006年周以真教授提出计算思维概念后，2010年她又指出计算思维是与形式化问题及其解决方案相关的思维过程[3]。计算思维的核心是抽象和自动化，那么什么是形式化问题的抽象呢？研究认为，它抽象的不是事物的因果关系，而是问题的计算过程，利用计算机强大的计算力去自动完成，是一种基于计算机的思维方式。本研究将问题从6个方面进行分类，力争凸显计算思维的本质及内涵。第一类问题属于数学类，第二类问题属于数学+形式化类，其余为形式化类问题。

（1）枚举类问题。典型代表为“鸡兔同笼”、“百钱百鸡”，这类题本质上无差别，仅情境不同，复杂度不同[4]。除此以外，数论中的寻找素数、合数、素数筛选法等都属于复杂度更高的该类问题。信息数字化类的，如“抓小偷”、“谁在说谎”、“预测名次”等也是用枚举法来解决的，这类题目更能体现计算机作为工具解决现实生活问题的优势。

（2）作图类问题。典型代表为“小海龟几何”，它是Google面向教育者计算思维课程“模式发掘”类题目之一。它通过绘制简单的正n边形，培养计算思维分析问题的步骤：分解功能——将一个任务转换为一系列步伐和转向；模式识别——观察重复步伐和所画图形的边之间相互关系；抽象化——使用转向角度和步伐数目中的模式来深入了解步伐数目、角度和多边形的是这是数学思维求解，用计算思维怎么求π呢？我们采用蒙特·卡罗方法（Monte Carlo method），它是以概率统计理论为指导的一类非常重要的数值计算方法，使用随机数（或伪随机数）来解决很多计算问题的方法。下面用蒙特·卡罗法求解。在一个单位长度为1的正方形内（如图1所示），连接对角线两点形成一段1/4圆弧，向正方形内随机撒点，通过计算落在1/4圆内与正方形内随机点数的比值，再乘以4，即求得π。撒点数越多，π值越精确。通过Python语言编程（如图2所示）和显示结果（如图3所示）看到，14行代码实现了向正方形内撒了一百万个点，求得的π值很精确，且只花费1.21秒。这种设计方法只关心过程的设计和构造，不管因果关系。它尤其适用于那些没有数学通项公式的问题，如四色定理，旅行商问题，最大梅森素数，股市中的量化分析，通过MM5模型预测天气预报等。数目之间关系；自动化——执行完成作图任务[5]。“画笔”提供的运动控制和方向控制功能使小海龟可以绘制很多复杂图形，如玫瑰花、人物肖像等。类似的工具还有“蟒蛇绘图”（Python语言）。

（3）递归类问题。典型代表为“汉诺塔”。哈工大的战德臣教授将递归列为“计算之树”的树根——三大奠基维度之一（其余两个是二进制和程序）[6]。汉诺塔没有一个数学模型加以求解，但是从形式化的角度递归地分析这个过程能够很容易地解决它。让我们来分析一下汉诺塔的移动过程。我们的目的是将n个盘子从A移到C，那么先将上面n-1个盘子从A移到B，把第n个盘子从A移到C之后，要考虑再将n-1个盘子从B移到C，怎么移呢？谁也不知道，也不用知道，我们只关心将n拆解为和n-1的关系，即只关心递归过程（递归链条）和终止条件（递归基例），至于n-1具体怎么做，我们不管，这就是形式化。程序并没有拆解该怎么移动盘子，只是将递归过程和终止条件通过函数加分支结构表达出来，剩下的交由计算机完成就行了。同类的问题还有科赫雪花等。该类问题共同点是大问题可不断地拆分为小问题，且大、小问题的性质相同。

（4）数学难题类。我们知道求数学中π值的表达式

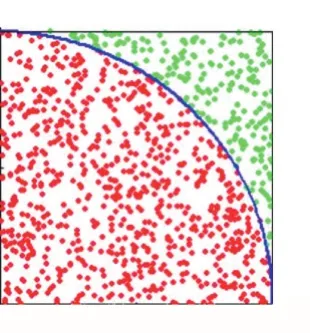
图1 边长为1的正方形

图2 Python程序蒙特·卡罗法求π值

图3 求π值结果和运行时间

（5）模拟仿真类。这类问题体现了计算思维与自然科学的交叉应用，如物理学、化学、生物学、医学[7]等。现在很多科学实验无法在实验室中进行，例如物理学，研究对象太过微小（例如亚原子微粒），或者需要一个没有重力的实验环境。化学的反应极为迅速，电子从一个原子核迁移到另外一个原子核需要百万分之一秒，经典化学难以跟上这样步伐，想借助实验方法去描绘化学过程中每一个步骤是不可能的，所以化学一半以上实验是在计算机上模拟实现的。下面举一个物理弹球的例子，用以模拟自由落体运动。该案例在Scratch中实现，为了看清楚它的轨迹（如图4所示），特增加了横向X轴方向的速度。

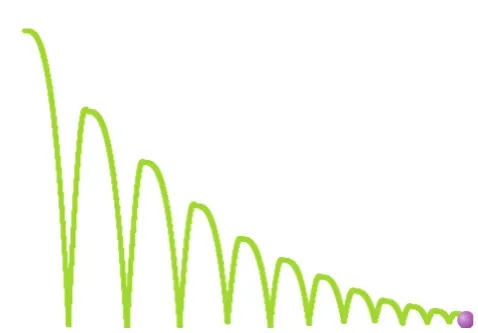
图4 模拟自由落体运动的小球轨迹

这类问题拓展题目很多，如霰弹枪算法大大提高了人类基因组测序的速度，蛋白质结构可以用绳结来模拟，用计算机模拟探测引力波及气候变暖等问题。

（6）社会科学类。这类问题体现了计算思维与社会科学的交叉应用[8]。如十九大报告中出现频率最多的前5个词是什么？威廉莎士比亚的著作是否全部为亲笔所著？下面以计算十九大报告词频统计为例说明。15行代码（如图5所示）瞬间就统计出了十九大报告排名前10的关键词（如图6所示），可以看出中国当前第一要义是发展。另外，聊天机器人、制作音乐[5]等都属于社科类。

图5 Python程序十九大报告词频统计

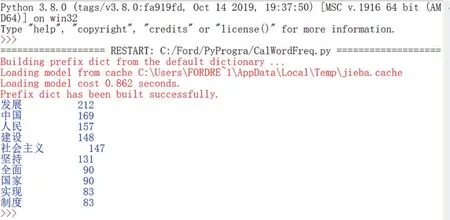
图6 十九大报告词频统计结果

2 培养计算思维的教学设计

2.1 教学目标

理解计算思维内涵，运用计算思维步骤解决具体问题，培养计算思维能力，促进核心素养形成。

2.2 教学内容

著名教育家裴斯泰洛齐指出，循序渐进性是心理化教学的重要原则，正如智慧和才能的发展一样，教学“要有一个适合人类本性的、心理学的、循序渐进的方法”，应该“在一切学科中尽力循序渐进地安排知识结构[9]。”信息技术是发展中的新兴学科，就把握学科思维的途径而言，自下而上更具有可操作性，尤其对于一线教师而言，从学科知识切入，向上探寻学科思维，是比较理想的方式[4]。依据此原则，本模块的教学内容应按照上述第一到第六类的顺序安排。第一类“数学成分”最多，学生经验丰富，课程内容熟悉，可顺利地“同化”新知识。第二类可将简单的已有知识与计算思维的本质特点一一对应起来，体验了计算思维的分析过程。从程序的逻辑结构来看，前两类包含了顺序、选择、循环3种结构，为后续编程奠定了基础。第三类是形式化抽象的突出体现，汉诺塔的迷人加上处理的巧妙，让学生领悟到了计算思维魅力，理解了它的内涵。第四类通过从工程学的角度求π值，拓宽了视野，完成了对计算思维的建构。第五类和第六类让学生看到了计算思维与多学科的交叉渗透以及在生活中的应用价值。这六类顺序的安排帮助学生完成了从同化到顺应的认知发展。

2.3 教学策略

（1）工具选择

编程是计算思维变成现实的主要手段。现今，Scratch、Blockly、Kodu等可视化编程工具日益丰富，极大地降低了学生参与程序开发的难度[11]，随着国内流行的编程猫Codemao、Google在线可视化编程工具pen⁃cilcode的加入，课堂上可选择手段变得更多。鉴于Scratch在我国中小学的普遍应用及编程猫基于Python语言的特点，推荐这两个作为可视化编程工具。Python语言已经被浙江、山东等几个省列为高考语言，因为它是目前最接近自然语言的通用编程语言。从语法角度看，它具备以下几个特点：①变量无须定义直接使用，具有独立的字符串类型；②简化了多语言文本的操作，对中文有良好的支持；③通过使用变长列表而不是定长数组，兼容多种数据类型并灵活表达集合长度；④代码简洁，支持面向过程和面向对象两种程序设计方法，代码行数可以缩减为C语言同样功能的1/5到1/10。该语言只关心计算问题的求解，其轻量级的语法和高层次的语言表示表达了应用计算机解决问题的计算思维理念[11]。所以Python成为必选。美国教育家爱德加·戴尔的“经验之塔”和视听教学理论告诉我们，直观的教学媒体能够帮助学生更好地理解抽象知识，故建议使用微课、视频等多媒体手段。从意义学习角度看，思维导图等可视化认知工具实现了学习者新旧知识之间的连接，促进了有意义学习的发生；从认知负荷理论看，可视化通过将小的组块组装成大的组块，降低了大脑的认知负荷，所以要用思维导图可视化思维过程[12]。

（2）教学组织

基于项目的学习（PBL）是“以学生学习为中心”的一种教学组织方式[13]，《课程标准》中建议采用项目活动创设问题情境，引导学生在解决问题的过程中感受信息技术对日常生活的影响，探究知识，提高能力，发展计算思维，因此课堂上应采取项目创设情境的方式导入教学，激发学生兴趣，提出任务。按照设计思维的第3个步骤，应该组织学生小组合作进行“头脑风暴”，这个阶段，教师一定要使每个小组明确任务，择机给出建议和指导，使学生的讨论沿着问题解决的方向展开[14]，体现出“学生主体、教师主导”的理念。在项目分析时，教师可采用思维导图模式分解，程序流程图抽象过程。程序实现阶段，采用自主探究+小组合作+成果推介+教师讲授的形式，使用Scratch（或编程猫）或Python语言完成。学习迁移是对知识的深入加工，在习得知识的同时提升了思维能力，是思维教学的有效手段[12]，上述六类问题中的每一类都列举了多个候选任务，供教师作为“举一反三”使用。

2.4 教学评价

如果以小组为单位展示作品，个人得分为小组得分结合个人在作品中的贡献率；如果是个人作品，可采用互评、自评等多元评价方式，也可采用一些测评工具，例如Dr.Scratch专门测量Scratch作品成绩[15]。无论采用哪种形式，一定本着评价是激励、促进教学，发挥积极导向作用的原则。

3 结语

计算思维作为人类第三种思维方式，已经渗透进人们的学习、生活并在各学科领域中发挥着重要作用。中小学课堂要培养学生的计算思维，选择什么样的教学内容作为知识载体成为关键问题。本研究将计算思维在多个领域的应用分为六个方面，由浅入深，从数学问题到形式化问题，两段代码意在直观地认识并深入理解计算思维解决问题的方式，即如何抽象和自动化。最后提出了简要的教学设计方案，可作为一线教师课堂实践的参考。