一种基于进化算法的银行网点选址求解方法

范人胜，杜红涛，周丹，吴洪，陈俊，何勇

（1.广东省农村信用社联合社，广州 510000；2.珠海市长陆工业自动控制系统股份有限公司，珠海 519090）

0 引言

选址问题是运筹学和管理科学中经典的决策问题，有着巨大的经济和社会研究价值，其主要研究选择设施的数目同和确定设施的最优位置，实现为用户提供优质服务价值的目的。自1964年Hakimi提出选址问题[1]后，大大激发了选址问题的研究，许多学者投身到选址问题的理论研究中。Hedetniemi等人[2]在一个无权重的网络中选择一个设施点，并新设计了算法解决此类问题，文献[3]提出可变领域搜索和禁忌搜索结合的算法求解离散选址问题。Goldman研究在树状网上选择设施点的中值问题[4]，其方法为先任选网络上的一个节点，计算该节点的权重是否超过所有节点权重的一半，是则选为中值点。Berman等人[5]利用最大覆盖模型求解距离，并针对不同情形做了改进。在选址模型的应用中，大部分用于物流中心、医院、消防站等公共服务领域，在银行选址方面的应用研究相对较少[6]。

银行网点作为一种服务类公共商业设施，其服务理念是“以客户为中心”，银行网点选址合理与否不仅影响到人民的生活质量，也关系到企业的战略发展[7]，合理的银行网点选址在给人民带来生活便利的同时，也给企业带来更大的收益。银行选址作为一门重要的研究课题，学者们用不同的理论和方法对其做了探索和研究。文献[8]设计了基于LBI的网点选址算法对网点进行部署。杨柳等人[9]提出用GIS技术确定ATM机的布局。文献[10]利用复杂网络方法，提出基于复杂网络的网点选址优化模型。Richard[11]利用GIS空间交互模型进行网点选址研究。Philip等人[12]采用了Huff模型构建银行网点选址模型。目前大多数银行选址研究都是基于离散型的，即在给定的网络节点上选取银行网点的部署位置；而连续型选址研究较少，其是指在给定的整个备选区域选取最优的位置。连续型选址相对于离散型选址来说，位置的选取是全局范围内寻找，对于环境的适应性更强，求解的难度更大[13]，连续型选址属于NP难问题。本文研究的银行网点选址是基于连续型的，考虑到经济实用性以及成本问题,以银行网点到居民点的路径长度最小作为优化目标。

差分进化（DE）算法是一种启发式优化算法，具有受控参数少、鲁棒性强等特点，在约束优化、聚类优化和神经网络优化等方面得到了广泛应用[14-16]。该算法在变异方面使用了差分策略，提高算法的搜索效率，避免了变异方式的不足，其具备全局并行和高效搜索的特性[17-18]，适合解决连续优化问题。但初始种群的个体分布会影响到算法的全局收敛能力[19]，为此本文找寻了可以缩小网络覆盖半径的均值点，作为差分进化算法的初始位置，从而提出解决连续K中心网点选址问题的均值点差分进化（Mean Points DE，MDE）算法。

1 银行网点选址模型

本文采用几何方式，将网点选址问题转化为图论问题。网点位置选取的不同，将对居民的生活便利产生影响。如图1-（A）所示，四节点构成的网络图G1，假定无向边的长度都是2。图1-（B）在节点v3设定网点位置，网点S到最远居民点v4的距离为2；图1-（C）将v2选定为网点S的部署位置，网点S到最远居民点v4的距离为 4，对比图 1-（B）和 1-（C）可知，网点位置选取的不同，其到各居民点的距离将产生差异，进而影响居民的生活质量。银行网点选址问题的主要目标就是通过调整网点位置，最大限度地提高网点对居民的服务质量。

图1 银行网点选址问题

网点选址对应的网络拓扑图用G(V,E)表示，其中V(G)={v1,v1,···,vn}，V(G)是指n个网络节点构成的集合。lij为节点vi和vj的欧几里得距离，对于任意两节点vi和vj间的距离小于等于给定的半径r时（即lij≤r），称两节点互为邻接节点，且两节点之间有边相连，邻接节点间的所有边构成集合E(G)。

在银行网点选址中，需要设置网点为居民点提供服务，居民点会以距离其最小的银行网点作为其服务节点。假设给定网络G的规模为n，设置服务网点数量为K个，是网络G的邻接矩阵，如果e(vi,vj)∈E(G)，则eij=1，否则eij=0。最短距离矩阵为表示网络G中节点vi到vj的最短路径距离，最短距离矩阵可由Floyd算法求得。如果d(vi,uj)≤d(vi,ul),j,l≤k,l≠j，则节点vi选择uj为其服务网点，此时网点uj的服务集Uj包含vi，即vi∈Uj。uj与服务集Uj中节点间最大的最短路径距离为，称为网点uj的覆盖半径。所有网点中的最大覆盖半径称为网点集的覆盖半径，也称为客户节点到网点集的路径长度。

服务网点集的覆盖半径是网点选址好坏的重要评价指标，覆盖半径越小，居民获得银行服务越便利。因此，银行网点选址问题的优化目标为网点集的覆盖半径最小，即路径长度最小，其模型为式：

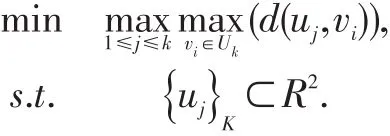
其中，R2为图G所在的二维平面。

根据网点设置位置不同，银行网点选址问题又分为离散K中心网点选址问题和连续K中心网点选址问题。离散K中心网点选址问题是在节点集V(G)中选取K个位置作为网点。而连续K中心网点选址问题是指在有界平面R2中无约束地选取K个位置并设置为网点，网点设置方式灵活高效。连续K中心网点选址相比于离散K中心网点选址，能够获得更小的覆盖半径。

图2 4客户节点网点部署示意图

同样以如图1-（A）的网络图为例。图2-（A）为离散K中心网点选址问题的选取方法，在V(G)中选择v2节点作为网点部署位置，全局最优的覆盖半径为4，图2-（B）为连续K中心网点选址问题的选取方法，在平面R2中选取一个合适的位置设置网点，覆盖半径降低为3，优于离散K中心网点选址问题的覆盖半径。连续K中心网点选址问题是指在整个网络平面范围内，选择任意K个位置来设置银行网点，因此连续K中心网点选址问题是NP难问题，难以通过经典数学方式进行精确求解。对于连续优化问题，进化算法有较好的求解效果。

2 基于改进差分进化算法的银行网点选址

差分进化（DE）算法是一种基于群体差异的随机搜索算法，该算法具有较强的搜索能力和鲁棒性，适合求解连续空间优化问题。针对连续K中心网点选址问题，初始种群的个体分布会影响算法的全局收敛能力，优化种群的初始位置，可提高算法的收敛效果。为此，本文引入了基于均值点的初始种群生成方法，提出了一种均值点的差分进化（MDE）算法。

2.1 MDE算法的初始化

在连续K中心网点选址的网络拓扑图中，规定两节点的距离lij≤r时，两节点之间有边相连，节点vi的覆盖范围是一个半径为r的球形邻域：Bi=如图3（A）所示的三节点网络图，其中r＜l(v1,v2)≤2r。如图 3（B）所示，阴影区D=B1⋂B2。若在双节点的阴影区D上部署网点节点，可以连通节点v1和v2，而v1和v2的中点c位阴影区内，在中点c处部署网点可以有效连接节点v1、v2和v3。中点c具有较好的连通性，可以有效缩短覆盖半径。因此，在平面R2上距离满足r＜lij≤2r的双节点具有重要意义，同理推广到任意双节点的情况。

图3 三节点网络图

在网络图G中，任意两个节点vi和vj，如果两节点之间的距离满足：r＜lij≤2r，则有Dij=Bi⋂Bj≠∅，称Dij为双节点vi和vj的公共覆盖区域。在Dij内的任意节点可与vi,vj同时建立连接，则Dij具有较好的连通效果，具有降低网点覆盖半径的潜质。而vi和vj所在直线的中点，根据圆的相交定理可知，中点cij∈Dij。因此可通过一个确定的点cij来代表公共覆盖区域，称点cij为网络图G的均值点，在均值点处部署网点，可以增加周边节点的连通性，达到降低网点覆盖半径的目的。

寻找到网络图G的全部均值点{cij}后，将均值点用于MDE算法的初始化。算法的初始化描述如下：随机选择均值点作为网点节点的位置，K个网点节点的位置坐标拼接成一个个体的初始位置。

2.2 MDE算法的编码表示和动态方程

MDE算法的第i个个体表示为：xi=(xi1,xi2,…,xim)。在连续K中心网点选址问题的求解过程中，MDE算法的每个个体代表网点选址问题的一组解，编码方式为K个网关在平面R2上的坐标位置的组合，网点选址的位置分别为：(a1,b1),(a2,b2),…,(aj,bj),…,(aK,bK)，其中aj=x2j-1;bj=x2j;m=2K。

MDE算法在迭代过程中，通过变异、交叉和选择更新个体的位置，从而搜索得到更加优秀的解。在种群初始化后，MDE算法通过差分策略实现个体变异。变异策略是随机选择两个不同的个体，将待变异个体与缩放后的向量差进行向量合成，产生一个变异向量。变异向量的计算见式（1）。

其中i≠r1≠r2≠r3，χ为缩放因子，vi(t+1)表示(t+1)时刻第i个变异向量。为了完善差分变异搜索策略，MDE算法使用了交叉操作。在(t+1)时刻，对种群中的目标个体与其变异向量进行个体间的交叉操作，如式（2）所示，其中CR为交叉概率，CR∈[0,1]，jrand为[1,2,3,···,2K]的随机整数。xi,j(t)表示t时刻第i个个体的第j位元素。

通过交叉操作后，得到目标个体的试验向量ui。交叉完成后，按照式（3）进行选择操作。

其中f(xi)为个体xi对应的适值。如果试验向量的目标函数值小于等于目标个体的函数值时，那么试验向量就取代目标个体进入下一代；否则目标个体就会继续保持到下一代中。通过比较每一个试验向量和被它们继承了参数的目标个体可以看出，MDE算法比其他进化算法更紧密地将交叉和选择结合起来。

2.3 MDE算法适值函数设计

在连续K中心网点选址问题中，适值函数越小，个体就越优秀，适值函数为个体的覆盖半径。MDE算法的每个个体代表K网点坐标位置的组合，因为个体可以降落到平面的任意位置，所以计算个体到居民节点的距离比较困难，可以采用如下方法进行计算。

个体的第k个网关uk的位置为ok=(ak,bk)，其中1≤k≤K。节点vi到其最近网点的距离为。则个体 (o1,o2,···,oK)的覆盖半径即该个体的适值为

2.4 MDE算法在网点选址中的实现

MDE算法的种群是随机产生的，每个个体代表网点选址的一组解，计算迭代过程中每个个体的适值，并记录种群的最小适值，MDE算法求解连续K中心网点选址的步骤如下：

Step1：初始化数目为PopSize的种群，在网络图的均值点出初始化种群的位置，并计算每个目标向量的适值，即覆盖半径R。

Step2：设定参数，确定缩放因子χ和交叉概率CR值。

Step3：根据式（1）对种群中的个体进行变异操作，产生变异后的中间体变异向量。

Step4：根据式（2）对变异向量和父代中的目标个体进行交叉操作，产生交叉后的试验向量ui。

Step5：计算交叉后的试验向量与父代中目标个体的适应值，根据式（3）产生新的一代种群。当满足F(ui)＜F(xi)时，ui取代目标个体原来的位置；否则，不取代。

Step6：当个体的适值收敛或达到了最大迭代次数时，算法结束运行；否则返回Step3。

算法的伪代码描述为：

3 仿真分析

本节的仿真环境是：MATLAB 2015a，内存8GB，CPU主频为2.5GHz的四核计算机。实验分别采用50、100、150和200节点规模的随机网络仿真连续K中心网点选址问题，网络图是连通的，节点度介于1和11，4种规模的网络拓扑如图4所示。实验以最小覆盖半径作为优化目标，将MDE算法与经典的PSO算法和GA算法进行实验结果对比。

图4 4种规模的网络拓扑图

3.1 算法在不同网络规模下的优化效果

表1为MDE、PSO、GA这3种算法在50,100,150,200不同规模随机网络中的优化结果，设定服务网点数目为5。表1分别记录了3种算法20次独立试验结果中，覆盖半径的最大值、最小值、平均值和标准差。

从表1对比3种算法的最小覆盖半径可知，MDE算法的各项指标要优于PSO算法和GA算法。MDE算法的标准差较小，稳定性较强。MDE算法与GA算法原理相同，都采用了变异、交叉和选择机制，但MDE算法在变异方面使用了差分策略，即使用了差分向量对个体进行扰动，实现个体变异，可以有效利用群体分布的特性，提高算法的搜索效率，避免了变异方式的不足。MDE算法和PSO算法都适合解决连续空间优化问题，但PSO算法在搜索过程中，容易陷入局部最优，搜索结果的鲁棒性较差，相比PSO算法，MDE算法的全局搜索能力强，搜索精度高，稳定性强。

表1 3种算法在不同节点规模下的覆盖半径结果

3.2 算法在不同网络规模下的收敛性过程

图5为MDE、PSO和GA算法在4种不同网络规模下的迭代收敛过程，A-D的网络规模分别为50,100,150,200节点。从图中可以看出，各算法初始值与收敛值差异较大，收敛过程对比明显。

图5 3种算法收敛过程分析

对比3个算法的初始值可知，GA算法的初始值最大，MDE算法与PSO算法的初始值相似，但稍微优于PSO算法。对比3个算法的收敛过程可知，GA算法和PSO算法收敛最快，容易陷入局部最优解；MDE算法收敛最慢，MDE算法的差分进化策略保障了种群多样性，收敛过程较慢，更易于收敛全局最优解。

3.3 算法在不同服务网点数目情况下的优化效果

表2为MDE、PSO、GA这3种算法在200网络规模情况下，设定不同服务网点数目，独立运行20次时，覆盖半径的最大值、最小值、平均值和标准差。

表2 3种算法在不同服务网点数目下的覆盖半径结果

从表2的实验结果可知，在服务网点数目一定的情况下，MDE算法的覆盖半径要优于PSO算法和GA算法，各项指标表现更优秀。GA算法解决的是离散K中心选址问题，服务网点部署在网络节点上，MDE算法和PSO算法解决的是连续K中心选址问题，服务网点部署在非邻接节点的中心位置，能够缩短其到周围节点的路径长度。

4 结语

针对银行网点选址问题，本文提出采用全局搜索能力较强的MDE算法解决连续型网点选址问题，以网点集的覆盖半径最小为优化目标，找寻了可以缩小覆盖半径的种群初始位置，并设计了新的适值函数。通过对比PSO和GA算法的实验结果，MDE算法收敛获得更加优秀的可行解。本文采用MDE算法解决连续K中心银行网点选址问题，为研究其他连续型设施选址问题提供了一种很好的解决方法。