一类含多奇性项的Grushin型算子方程解的渐近性质

张金国,杨登允

(江西师范大学数学与统计学院,江西南昌 330022)

1 引言

本文主要研究如下含多个奇性项和临界指数增长的非线性次椭圆型方程的非平凡解在奇点处的渐近性质

此外,非线性项f:Ω×R→R是Carath´eodory函数,且满足

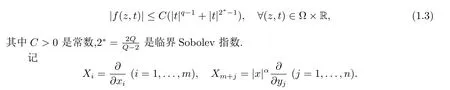
则Grushin梯度为∇α=(X1,...,XN),由此Grushin型算子可表示为

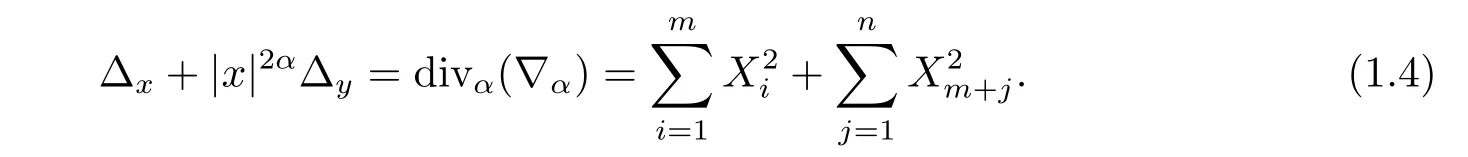
显然:当0时,该算子是椭圆型的,并且在流形{0}×上是退化的;当α是非负整数时,Grushin算子是H¨ormander型的.其它相关知识可以参见[1-5]等.

假设k≥2,对任意的i=1,2,···,k,定义

利用Moser迭代技巧,本文讨论了方程(1.1)的非平凡解在奇点处的渐近性质.结论如下.

(i)存在常数C,ρi>0使得

其中Bd(ai,ρi)表示在距离d的意义下以ai为圆心,以ρi为半径的球,且ajBd(ai,ρi),i,j=1,2,···,k,ij.

(ii)存在常数C>0使得

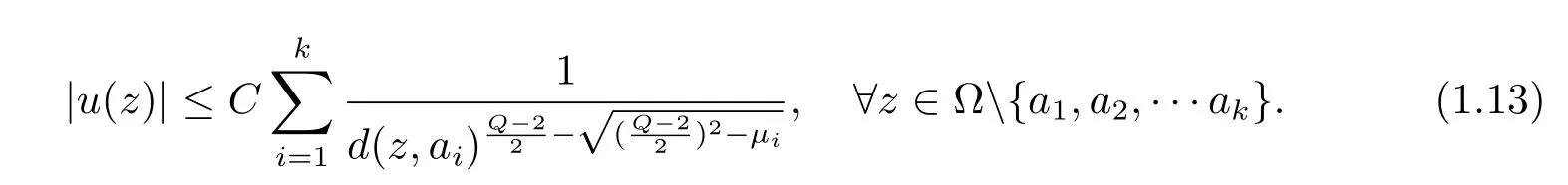
在欧式空间中,关于Laplace算子问题的相关结论可参考[7].利用Moser迭代和分析技巧,我们在第二节给出定理1.1的证明.对于退化的Grushin型算子和Carnot群上的次椭圆算子而言,该结论依然是新的.

2 定理1.1的证明

首先给出广义Hardy型不等式(1.11)的证明.

不等式(1.11)的证明令ρ=min{d(ai,al),d(ai,∂Ω)},i,l=1,2,···,k,. 则Bd(ai,ρ)∩Bd(al,ρ)=∅,其中Bd(a,ρ)={x:x∈Ω,d(x,a)<ρ}.由不等式 (1.7)和ψi<1(i=1,2,···,k) 可得

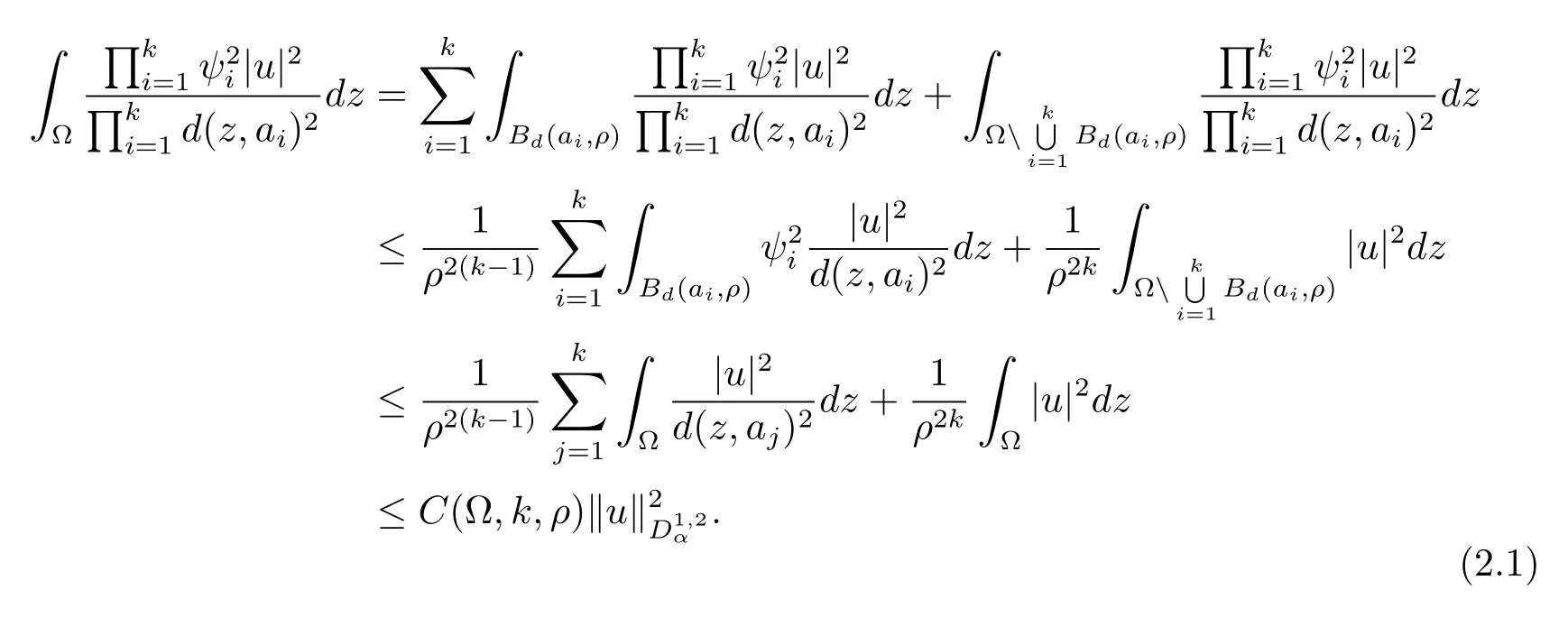
因此,不等式(1.11)得证.上述结论表明广义Hardy型不等式的最佳常数可如下定义:

为了估计方程(1.1)的非平凡解在原点处的渐近性质,我们需要如下的Lp估计.

证明引理2.2的证明与[1,命题3.2]或[7,引理3.1]证明过程类似.此处略.

为了研究方程解在奇点处的渐近性质,我们将Ω做如下分解

定理1.1的证明设u∈是方程(1.1)的解.令

从而将u=d(z,ai)−βv带入方程(1.1)的左边,由(2.4),(2.5)式可得

结合f(z,u)=f(z,d(z,ai)−βv)及(1.1),(2.6)可得

在(2.7)式两边同时乘上d(z,ai)−β,可得

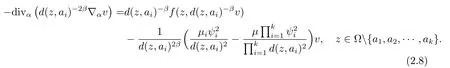
其中L,s>1在后面给定.将试验函数φ代入(2.8)式得

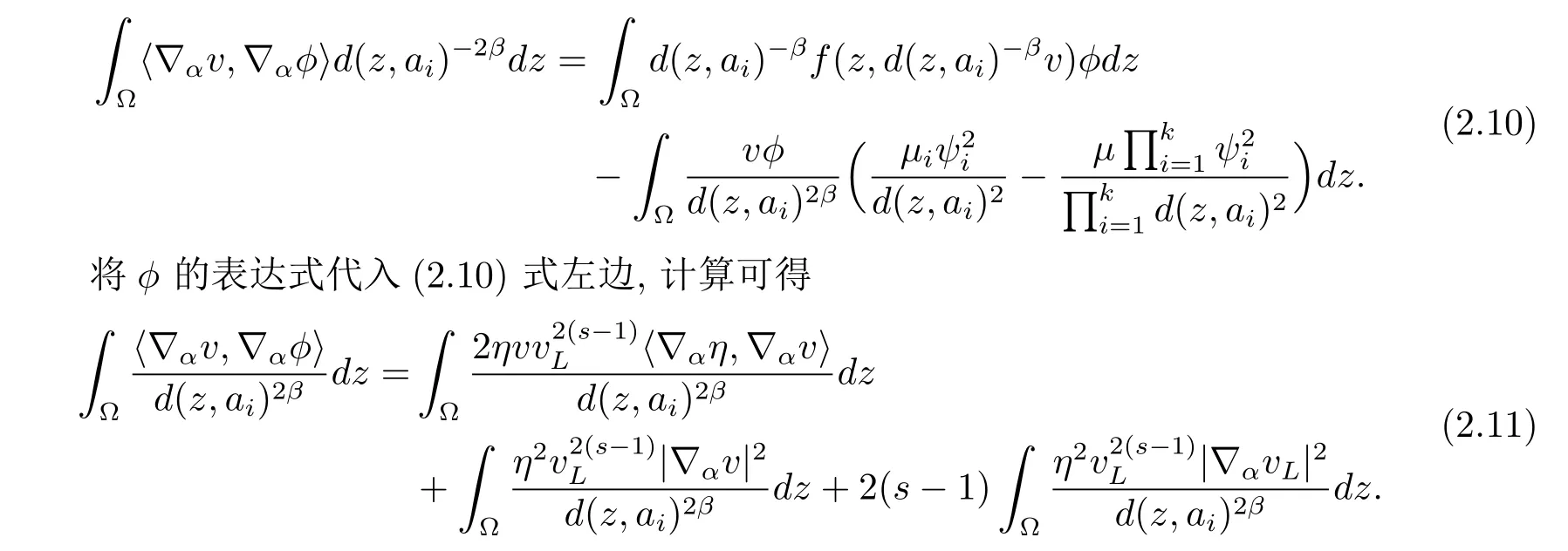
由Young不等式,对充分小的ε>0,存在C1(ε)>0使得

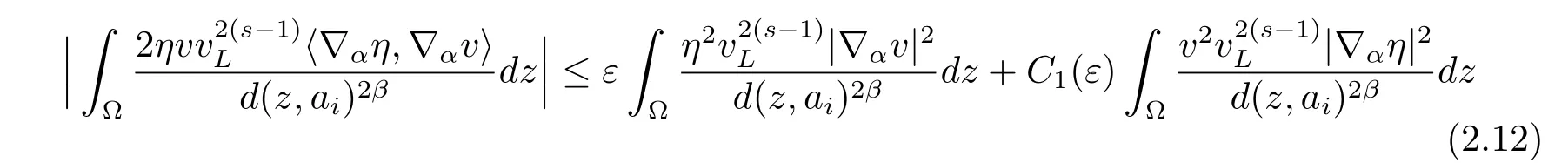
从而

将φ的表达式代入(2.10)式右边第一项中,利用函数f满足的条件(1.3)可得

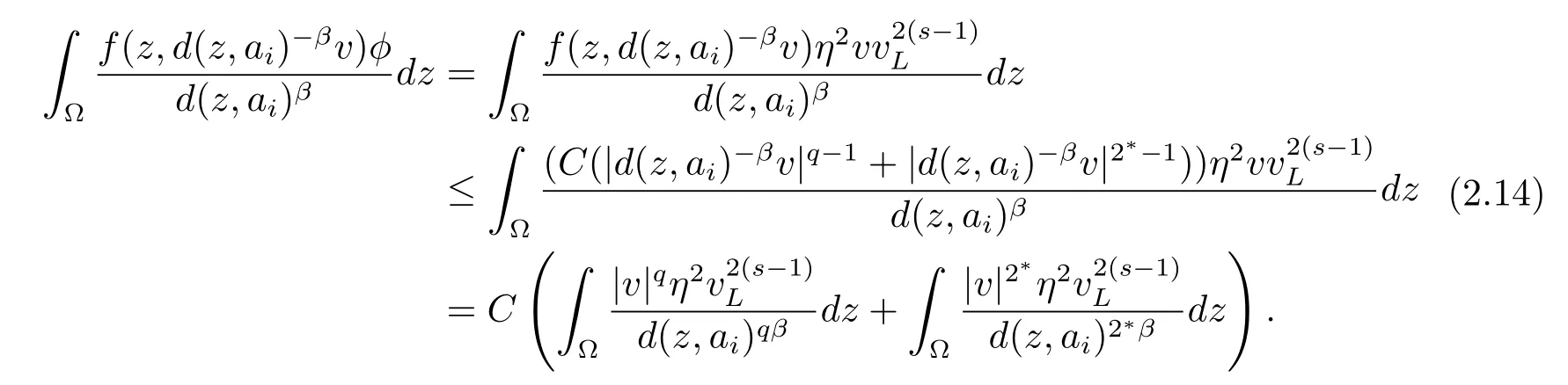
对于上式第一项利用不等式tq≤t2+(q∈[2,2∗))可得

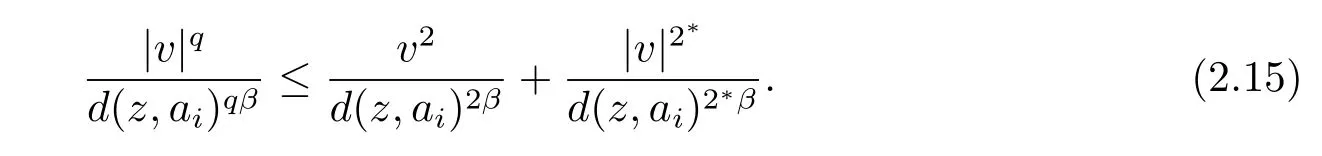
从而,存在C1,C2>0使得

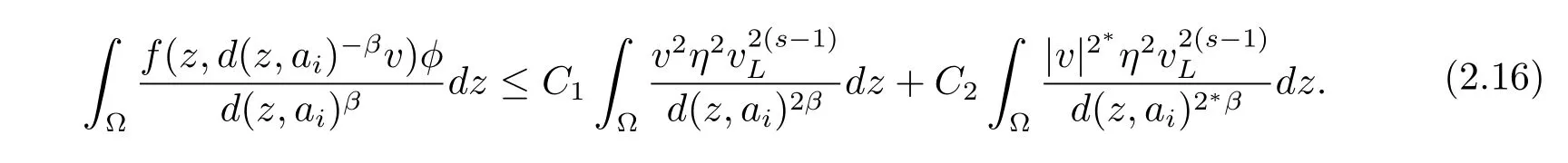
最后,将φ的表达式代入(2.10)式右边第二项中,利用µi的定义,中值定理,Young不等式和ψi<1可得

其中C3,C2(ε)是正常数.

下面利用如下形式的加权Sobolev不等式[3]对(2.17)的右端项做进一步的处理:

因此,结合(2.17),(2.19)式,(2.10)式右端第二项满足