ON THE CHARACTERIZATION OF COMPACTNESS IN THE SPACE OF HENSTOCK-KURZWEIL INTEGRABLE FUNCTIONS

GUO Ya-ting,YE Guo-ju,LIU Wei,ZHAO Da-fang

(1.College of Science,Hohai University,Nanjing 210098,China)

(2.School of Mathematics and Statistics,Hubei Normal University,Huangshi435002,China)

Abstract:In this paper,we are concerned with a classical question in the space of Henstock-Kurzweil(shortly HK)integrable functions.A negative answer to this question is given by using the theory of the distributional Henstock-Kurzweil(shortly DHK)integral.Furthermore,we use convergence to prove a sufficient and necessary condition for a function to be HK integral and then give a characterization of compactness in the space of the HK integrable functions.The results enrich and extend the theory of HK integrable functions space.

Keywords: Henstock-Kurzweil integral;distributional derivative;distributional Henstock-Kurzweil integral;convergence theorem;compactness

1 Introduction

It is well known that the HK integral of real-function comprises Riemann integral,Lebesgue integral,improper integral and it is equivalent to Perron integral and restricted Denjoy integral.A distinguishing feature of HK integral is that it can integrate highly oscillatory functions which occur in nonlinear analysis and quantum theory.It is also easy to understand because its definition requires no measure theory.Such integral has very wide applications in many fields,for instance,differential and integral equations([1-7]),Fourier analysis([8-11]),economics([12-15]),quantum theory([16,17])and so on([18-21]).Likewise,the theory of the HK integral were widely studied by many mathematicians and physicians,for example,Gill and Zachary([22]),Jan([23]),Kurtz and Swartz([24]),Lee([25,26]),Lee([9]),Monteiro([27]),etc..However,the space of HK integrable functions is not a Banach space.The more extensive applications of HK integrals are limited by the incompleteness of the space of the HK integrable functions.So,many people tried to solve this problem,for instance,Kurzweil[28,29].Meanwhile,Lee gave some open problems on the theory of the HK integral in the last few years.One of the problems is about the two-norm convergence in the space of the HK integrable functions which will be stated in Section 5.Inspired by this problem,a related question,which is Question 5.1 in Section 5,appeared naturally.

We give a negative answer to Question 5.1 by using the completeness of the space ofDHKintegral.TheDHKis a very wide integral and it includes Lebesgue and HK integrals.Denote the space of HK integrable functions byHKand called the Denjoy space[25],and the space of integrable distributions byDHK.DHKis a Banach space and it is isometrically isomorphic to the space of continuous functions on an closed interval with uniform norm.The Denjoy space is dense inDHK.

In Section 2,we present some basic definitions and preliminaries of HK integral of real functions.Section 3 is devoted to theDHKintegral and its properties.In Section 4,we prove two sufficient and necessary conditions for a distribution to be integrable.In Section 5 we firstly state Question 5.1 and then give a negative answer.In Section 6,we prove a sufficient and necessary condition for a function to be HK integrable and then give a characterization of compactness in the Denjoy space.

2 Basic Definitions and Preliminaries

LetI0=[a,b]be a compact interval inandE⊂a measurable subset ofI0.Letµ(E)denote the Lebesgue measure.We first extend the notion of a partition of an interval.

We say that the intervalsIandJare non-overlapping if int(I)∩int(J)=∅,where int(J)denotes the interior ofJ.

Apartial K-partition DinI0is a finite collection of interval-point pairs(I,ξ)with non-overlapping intervalsξ∈I⊂I0.We writeD={(I,ξ)}.Moreover,if the union of all the intervalsIequalsI0,thenD={(I,ξ)}is aK-partitionofI0.

Letδbe a positive function defined onI0which is called agauge.The symbol∆(I0)stands for the set ofgaugeonI0.AK-partitionD={(I,ξ)}is said to beδ- fineif for each interval-point pair(I,ξ)∈Dwe haveI⊂B(ξ,δ(ξ))whereB(ξ,δ(ξ))=(ξ−δ(ξ),ξ+δ(ξ)).LetP(δ,I0)be the set of allδ- fineK-partition ofI0.

GivenP∈P(δ,I0),we write

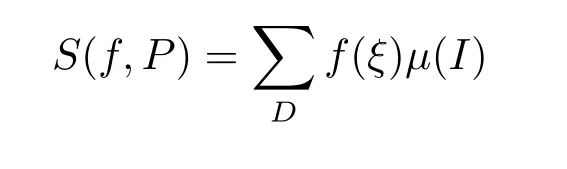
for integral sums overD,wheref:I0→.

Definition 2.1[24]A functionfis called HK integrable onI0with the HK integralJ=(HK)R(x)dx,if there exists aJ∈such that for everyε>0 there existsδ∈∆(I0)such that

for everyP∈P(δ,I0).The family of all HK integrable functions onI0is denoted byHKI0.fis HK integrable on a setE⊂I0if the functionf·χE∈HKI0.We write

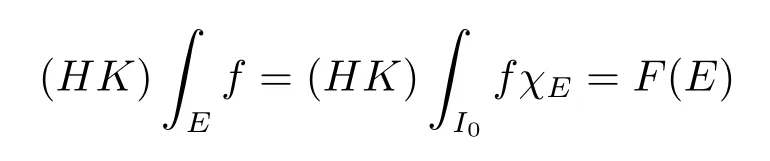
for the HK integral offonEwhereFis called the primitive off.

Definition 2.2[26,30]LetE⊂I0andF:I0→.F:I0→R is calledabsolutely continuousorAC∗onEif for everyε>0 there exists aη>0 such that

whenever{[vi,ui]}is a finite sequence of non-overlapping intervals which have an endpointvioruiinEand satisfyPi(ui−vi)<η.A family of function{Fn}is said to be uniformlyAC∗ifFnisAC∗but uniformly inn,i.e.,η>0 independent ofnwithFreplaced byFnin(2.1).

F:I0→R isACG∗(orFnis uniformlyACG∗)onI0ifI0can be expressed as a countable union of its subsetsEn,n∈Nsuch thatFisAC∗(orFnis uniformlyAC∗)on eachEn.

Lemma 2.3[25,26]Letf:[a,b]→.Iff∈HK[a,b],then the primitiveFoffisACG∗on[a,b].

Definition 2.4[25,26]fis called restricted Denjoy integrable(shortlyD∗)onI0if there exists anF∈ACG∗such thatF′(x)=f(x)a.e.onI0.

Lemma 2.5[25,26]TheHK-integral and theD∗-integral are equivalent.

The theory of distributions,or generalized functions,was founded by Schwartz L in the 1940’s and it extended the notion of function so that all distributions have derivatives of all orders.Distributions are defined as continuous linear functionals on the space of the functionsandφhas compact support in},where thesupportof a functionφis the closure of the set on whichφdoes not vanish.Denote it by

For allf∈D′,we define the distributional derivativef′offto be a distribution satisfying〈f′,φ〉=−〈f,φ′〉,whereφis a test function.Further,we write distributional derivative asf′.If a functionfis differentiable,then its ordinary pointwise derivative denotes asf′(x)wherex∈.From now on,all derivative in this paper will be distributional derivatives unless stated otherwise.

3 The Distributional Henstock-Kurzweil Integral

LetIbe an open interval in,we define

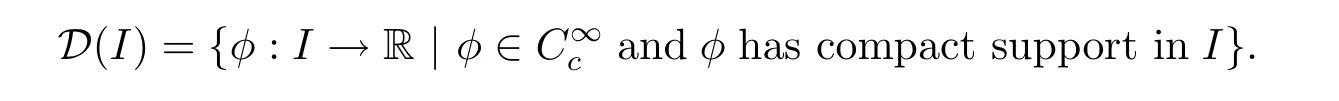
Then the distributions onIare the continuous linear functionals onD(I).The space of distributions onIis denoted byD′(I),which is the dual space ofD(I).SinceD(I)⊂D,soD′⊂D′(I),i.e.,iff∈D′thenf∈D′(I).

Denote the space of continuous functions on[a,b]byC([a,b]).Let

ThenC0is a Banach space under the norm

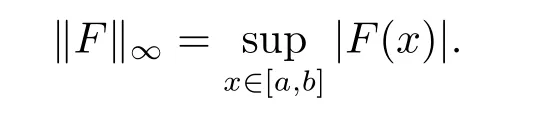
Definition 3.1A distributionfinD′((a,b))is said to be distributionally Henstock-Kurzweil integrable(shortlyDHK)on an interval[a,b]if there exists a continuous functionF∈C0such thatF′=f,i.e.,fis the distributionalderivative ofF.The distributional Henstock-Kurzweil integral offon[a,b]is denoted by=F(b)−F(a),for short,

For everyf∈DHK,φ∈D((a,b)),we write〈f,φ〉=−〈F,φ′〉=−

In symbols,

Of course,DHKis a subset ofD′((a,b)).

Notice that iff∈DHKthenfhas many primitives inC([a,b]),all differing by a constant,butfhas exactly one primitive inC0.For simplicity of notation,in what follows we use the lettersF,G,...for the primitives off,g,...inDHK,respectively.Unless otherwise stated,“” denotes theDHK-integral throughout this paper.

Remark 3.2If takinga=−∞andb=+∞,we obtain distributional Henstock-Kurzweil integral on=[−∞,+∞]as in[31].ForDHKintegral on,we can similarly discuss all properties as on[a,b].

Forf∈DHK,define the Alexiewicz norm inDHKas‖f‖=‖F‖∞.With the Alexiewicz norm,DHKis a Banach space(see[31]).

Lemma 3.3[31](a)The space of all Lebesgue integrable functions and the spaces of restricted Denjoy and wide Denjoy integrable functions are dense inDHK.

(b)DHKis a separable space.

Since the primitiveFof a HK integrable functionfis continuous andF′(x)=f(x)is almost everywhere.It is easy to see thatHK⊂DHK.By Lemma 2.5 and Lemma 3.3,the following corollary holds.

Corollary 3.4The spaceHKis dense inDHK.

Letg:[a,b]→,its variation isV(g)=where the supremum is taken over every sequence{(xn,yn)}of disjoint intervals in[a,b].A function g is of bounded variation on[a,b]ifV(g)is finite.Denote the space of functions of bounded variation byBV.The spaceBVis a Banach space with norm‖g‖BV=|g(a)|+V(g).

Recall thatC([a,b])∗=BVby the Riesz Representation Theorem.SinceC0is the space of continuous functions on[a,b]vanishing ataandDHKis isometrically isomorphic toC0due to the definition of the integral,an obvious fact is that the dual space ofDHKisBV(see details in[31]).

Furthermore,integration by parts and H¨older inequality hold.

Lemma 3.5[31](Integration by parts)Letf∈DHKandg∈BV.Thenfg∈DHKand

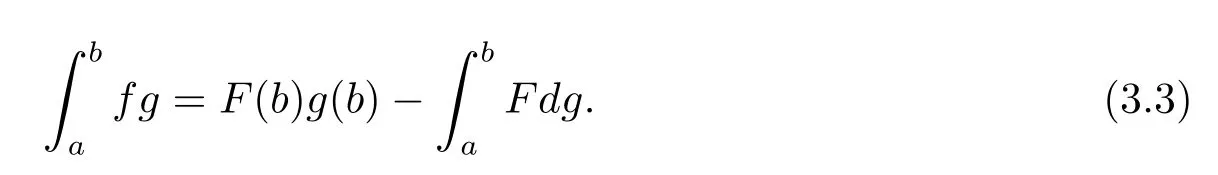
Lemma 3.6[31](H¨older inequality)Letf∈DHK.Ifg∈BV,then

Note thatDHKis a Banach space under the Alexiewicz norm‖.‖,there are several equivalent norms as follows(see details in[31,Theorem 29]).

Forf∈DHK,define

Recall thatHKis not a Banach space under the norm‖f‖HK=So we have

Proposition 3.7HKis not complete under the norms‖.‖1,‖.‖2.

Remark 3.8HK⊂DHKandDHKis complete.So,extending theHKtoDHK,it overcomes the defect of the spaceHKnot being complete.

4 Sufficient and Necessary Condition in DHK

In this section we discuss the convergence problems of the sequence{fng}forfn∈DHKandg∈BVand then we give two sufficient and necessary conditions for a distribution to be integrable,which plays a significant role in answering Question 5.1 in the next section.

LetO(BV)be the unit ball inBV,i.e.,

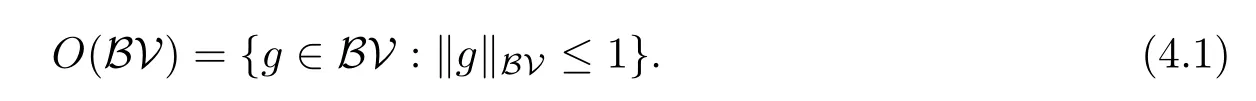
Now we use Lemma 3.3 and Corollary 3.4 to prove a weak convergence theorem.

Theorem 4.1Letf∈DHK.Then there exists a sequence{fn}of HK integrable functions such that

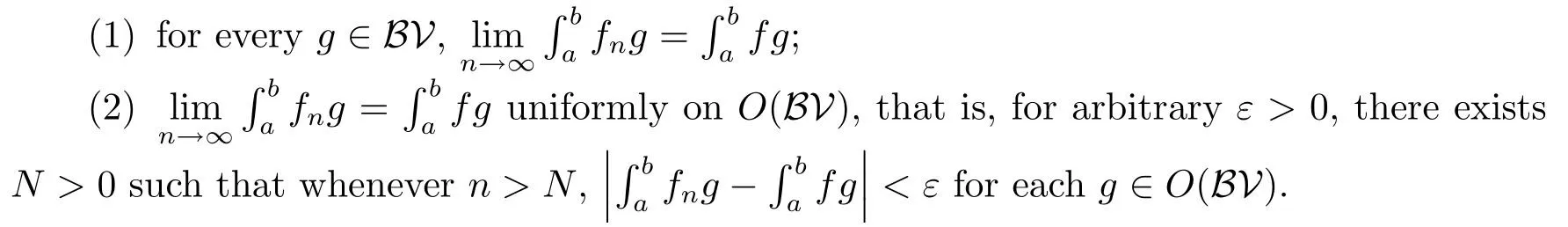
Proof(1)By Lemma 3.3,the spaceDHKis a separable Banach space.By Corollary 3.4,the spaceHKis dense inDHK.So,forf∈DHK,there exists a sequence{fn}of Hk integrable functions satisfying

whereFnandFare the primitives offnandf,respectively.

Sincefn∈HK,fn∈DHK.Forf∈DHKand everyg∈BV,by Lemma 3.5,we havefg∈DHK.By Lemma 3.6,

The converse of Theorem 4.1 is also true.

Theorem 4.2Assume that{fn}is a sequence of HK integrable functions satisfying

(1)for everyg∈BV,converges;

Then there existsf∈DHKsatisfying

Thus,{〈fn,g〉}is a Cauchy sequence.

Since for eachn,m∈,

It follows from uniform convergence ofonO(BV)that{fn}is a Cauchy sequence inDHK.

By Lemma 3.3,the spaceDHKis a Banach space,so there existsf∈DHKsuch that=finDHK.Hence,we have

and

The proof is complete.

Combining Theorem 4.1 with Theorem 4.2,we get a sufficient and necessary condition for a distribution to be integrable.

Theorem 4.3A distributionf∈DHKiffthere exists a sequence{fn}of HK integrable functions satisfying(1)and(2)in Theorem 4.2.

Based on Theorem 4.3,we can prove another sufficient and necessary condition for a distribution to be integrable.

Theorem 4.4A distributionf∈DHKwith the primitiveFif and only if there exists a sequence{fn}of HK integrable functions with the primitivesFnsatisfying

(1){Fn}is bounded inC([a,b]);

Moreover,

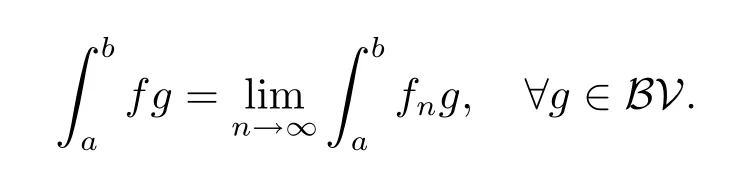
The fact thatf∈DHKimpliesF∈C0⊂C([a,b]).This shows that(2)holds.

(Sufficiency)Sincefn∈HK,Fn(a)=0(n∈N).By hypothesis(2),fromF(a)=Fn(a)=0,it follows thatF∈C0.Definef=F′.Thenf∈DHKand

Moreover,since{Fn}is bounded inC([a,b]),by dominated convergence theorem of Riemann-Stieltjes integral,

Hence,by Lemma 3.5,we have

The sufficiency is complete.

5 Question and Answer

P.Y.Lee asked an open problem on the two-norm convergence in the Denjoy space.The two-norm convergence of a sequence of functions often means that the sequence is bounded in the strong topology and convergent in the weak topology.We call it Lee’s problem which is stated as follows:

Lee’s problemTwo-norm convergence.The controlled convergence does not generate a topology inHK,and the condition of almost everywhere convergence seems to be too strong.Can we define a two-norm convergence inHKso that the two-norm convergence will generate a topology inHK?

Inspired by this problem,a related question appeared naturally and can be stated as follows.

Question 5.1Let{fn}⊂HK[a,b].If the sequence{fn}is bounded inHK[a,b]and{(HK)}converges for everyg∈BV,whether there existsf∈HK[a,b]such that

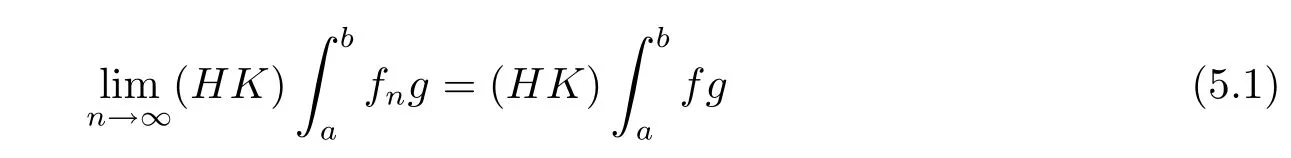
for everyg∈BV?

Recall that(HK)fdenotes the HK integral offon[a,b].

Let us see an example first.

Example 5.2Suppose thatx∈[0,1].Let

Then

for allx∈[0,1].Since for eachn∈,the functionFn(x)is continuous on[0,1]andFn(x)uniformly converges toF(x),soFis continuous on[0,1]andF(0)=0,which implyF∈C0.ButF,apart from certain exceptional points,is not differentiable on[0,1].

Let

Thenf∈DHKand

However,[0,1].

In fact,iffin(5.2)is HK integrable on[0,1],then its primitiveFis differentiable for almost allx∈[0,1].It is a contradiction.So[0,1].

On the other hand,let

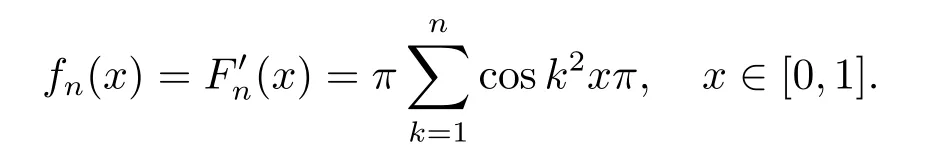
Thenfnare continuous on[0,1]and thereforefnare HK integrable on[0,1],and

Since

It follows thatFn(x)are uniformly bounded on[0,1].Hence,for everyg∈BV,by dominated convergence theorem of Riemann-Stieltjes integrals,we obtain that

Combining(5.4)with Lemma 3.5,we have

So,the sequence{fn}is bounded inHK[a,b]and weakly converges tof,butfis not HK integrable.

Therefore,according to Example 5.2,we can give an answer to Question 5.1.

Theorem 5.3Let{fn}⊂HK[a,b].Asuume that{fn}is bounded inHK[a,b]and{(HK)}converges for everyg∈BV.Then it is not necessary that there exists a functionf∈HKsuch that for everyg∈BV,

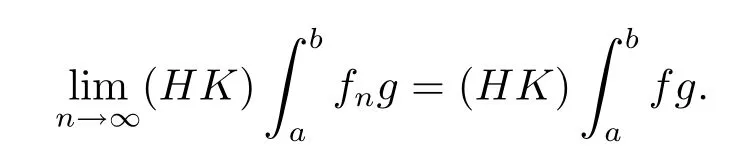
In order to further discuss the related problems with Question 5.1,we give a necessary and sufficient condition for a function to beHKintegrable in the next section.

6 Compactness

Firstly,we prove a necessary Lemma.

Lemma 6.1Assume that{fn}is a sequence of the HK integrable functions on[a,b]satisfying

(1)for everyg∈BV,{(HK)}converges;

(2)the sequence{Fn}of the primitives offnis uniformlyACG∗.

Then there existsf∈HK[a,b]satisfying

The proof is complete.

Lemma 6.2Assume thatf∈HK[a,b].Then there exists a sequence{fn}of HK integrable functions on[a,b]satisfying

(1)for everyg∈BV,{(HK)}converges to(HK)

(2)the sequence{Fn}of the primitives offnis uniformlyACG∗.

ProofLetf∈HKwith primitiveF∈ACG∗.According to[26,p198,Exercise 5.7],there is a sequence{ϕn}of step functions such thatϕn→fis almost everywhere and the primitives Φnofϕnare uniformlyACG∗.Due to the definition of uniformlyACG∗,Φnis uniformly bounded and equicontinuous on[a,b].In view of[26,Lemma 5.5.1],there is a subsequenceof Φnsuch thatconverges uniformly toFon[a,b].DenotebyFn.Of course,Fnare uniformlyACG∗.By virtue of the controlled convergence theorem([26,Theorem 5.5.2]),one has

Moreover,it follows from Lemma 3.5 that

The fact thatFnconverges uniformly toFon[a,b]and the dominated convergence theorem for Riemann-Stieltjes integrals yield that,for eachg∈BV,

which together with(6.1)implies that,for eachg∈BV,

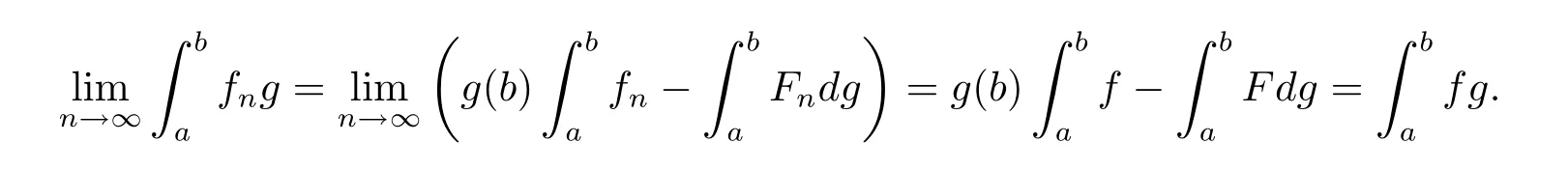
Therefore,the proof is complete.

By Lemma 6.1 and Lemma 6.2,we obtain a necessary and sufficient condition for a function to beHKintegrable.

Theorem 6.3f∈HK[a,b]iff there exists a sequence{fn}of HK integrable functions on[a,b]satisfying(1)and(2)in Lemma 6.2.

Now we are coming to give a characterization of the compact subsets inHK.

Theorem 6.4Assume thatA⊂HKandB={F:F(t)=f,f∈A}.ThenAis relatively compact inHKif and only if for every sequence{fn}⊂A,there exists a subsequenceof{fn}such thatsatisfies(1)and(2)in Lemma 6.2.

ProofThe proof is directly deduced from Theorem 6.3.