K-ORDER GENERALIZED DERIVATIONS OF WEIGHT λ ON δ JORDAN-LIE TRIPLE SYSTEMS

LIU Ning,ZHANG Qing-cheng

(1.School of Mathematics,South China University of Technology,Guangzhou 510604,China)

(2.School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China)

Abstract:This paper deals with the k-order generalized derivations of weight λ on δ Jordan-Lie triple systems.By computing,we conclude that every k-order Jordan triple θ-derivation of weight λ on δ Jordan-Lie triple systems is a k-order θ-derivation of weight λ.Under the definitions,we give another equivalent form of k-order Jordan triple θ-derivation of weight λ.Meanwhile,We also establish the inheritance property of k-order generalized(θ,ϕ)-derivation of weight λ and Rota-Baxter operator of weight λ on Rota-Baxter δ Jordan-Lie triple systems.We obtain that every Rota-Baxter δ Jordan-Lie algebra can be seen as a Rota-Baxter δ Jordan-Lie triple system.

Keywords: δ Jordan-Lie triple systems;k-order(θ,ϕ)-derivations;k-order Jordan triple(θ,ϕ)-derivations;weight λ;Rota-Baxter δ Jordan-Lie triple systems of weight λ

1 Introduction

Lie triple systems have played an extremely important role in mathematics and physics for a long time.The concept of Lie triple systems was first introduced by N.Jacobson[1],[2](see also[3]).As the generalization of Lie algebra,δJordan-Lie algebra was first introduced in[4].LetRbe a commutative ring with a unit.AδJordan-Lie algebra is aR-moduleLwith aR-bilinear mappingL×L∍(x,y)[x,y]∈Lsatisfying the following conditions:

for allx,y,z∈L.δ=±1.Forδ=1,these equations represent the Lie algebra[5].Similarly,we can obtain the definition ofδJordan-Lie triple system in[4].AδJordan-Lie triple system is aR-moduleLwith aR-trilinear mappingL×L×L∍(x,y,z)[x,y,z]∈Lsatisfying for allu,v,x,y,z∈L.δ=±1.The case ofδ=1 gives the Lie triple system[5].Clearly,everyδJordan-Lie algebra with product[·,·]is aδJordan-Lie triple system with respect to[x,y,z]:=[[x,y],z].

As is well known,derivations and generalized derivation algebras are very important subjects both in the research of rings and Lie algebras.In the study of Levi factors in derivation algebras of nilpotent Lie algebras,the generalized derivations,quasiderivations,centroids and quasicentroids play key roles(see[6]).The most important and systematic research on the generalized derivative algebras of Lie algebras and their subalgebras were due to Leger and Luks.Much work have been done in this area,showing an interesting derivation and generalized derivative algebras(see[7-17]).In particular,some nice properties of the generalized derivation on Lie triple systems have been obtained in[16-17].

In[18-20],the concepts of Rota-Baxter 3-Lie algebras were introduced and the authors studied the inheritance property of Rota-Baxter 3-Lie algebras and Rota-Baxter Lie triple systems.They introduced the concepts of a Rota-Baxter operator and differential operator with weights on Lie triple system.Rota-Baxter operators on Lie algebras are operator forms of the classical Yang-Baxter equations and contribute to the study of integrable systems[6],[18-23],[25-29].

The paper is organized as follows.In section 2,we conclude that every k-order Jordan tripleθ-derivation of weightλonδJordan Lie triple system is a k-orderθ-derivation of weightλand we give another equivalent form of k-order Jordan tripleθ-derivation of weightλonδJordan-Lie triple systems.In section 3,we establish the inheritance property of k-order generalized(θ,ϕ)-derivation of weightλon Rota-BaxterδJordan-Lie triple systems of weightλand generalize some results in[18]to Rota-BaxterδJordan-Lie triple systems of weightλ.

2 On K-Order Generalized Derivation of Weight λ on δ Jordan-Lie Triple Systems

The purpose of this section is to study a k-order derivation and k-order generalized derivation of weightλonδJordan-Lie triple system.In particular,we generalize some results in[16]-[17]to k-order(generalized)derivation of weightλonδJordan-Lie triple systems.We first introduce the concepts of k-order(generalized)(θ,ϕ)-derivations of weightλand k-order(generalized)Jordan triple(θ,ϕ)-derivations of weightλonδJordan-Lie triple systems.Then we prove that every k-order generalized Jordan triple(θ,ϕ)-derivation of weightλon Lie triple system is a k-order generalized(θ,ϕ)-derivation of weightλunder some conditions.In particular,we conclude that every k-order Jordan tripleθ-derivation of weightλon Lie triple systems is a k-orderθ-derivation of weightλ.In the end we give another equivalent form of k-order Jordan tripleθ-derivation of weightλonδJordan-Lie triple systems.

Given an integern>1,a ringRis said to ben-torsion free,if forx∈R,nx=0 implies thatx=0.

Definition 2.1LetLbe aδJordan-Lie triple system over ringR.Letθ,ϕ:L→LbeR-linear maps.AR-linear mapD:L→Lis called a k-order(θ,ϕ)-derivation of weightλ∈RonLif

for allx,y,z∈L,λ∈R.δ=±1.Ifϕ=θ,a k-order(θ,ϕ)-derivation of weightλis called a k-orderθ-derivation of weightλ.Ifϕ=θ=IL,whereILis the identity map onL,a k-order(θ,ϕ)-derivation of weightλis called a k-order derivation of weightλ.

Remark 2.2Ifλ=0 andδ=1,a k-order(θ,ϕ)-derivation of weightλcould be seen as a(θ,ϕ)-derivation(see[16]-[17]).

Definition 2.3LetLbe aδJordan-Lie triple system over ringR.Letθ,ϕ:L→LbeR-linear maps.AR-linear mapD:L→Lis called a k-order Jordan triple(θ,ϕ)-derivation of weightλ∈RonLif

for allx,y∈L,λ∈R,δ=±1.Ifϕ=θ,a k-order Jordan triple(θ,ϕ)-derivation of weightλis called a k-order Jordan tripleθ-derivation of weightλ.Ifϕ=θ=IL,whereILis the identity map onL,a k-order Jordan triple(θ,ϕ)-derivation of weightλis called a k-order Jordan triple derivation of weightλ.

Remark 2.4Ifλ=0 andδ=1,a k-order Jordan triple(θ,ϕ)-derivation of weightλcould be seen as a Jordan triple(θ,ϕ)-derivation(see[16,17]).

Definition 2.5Letα:L→Lbe a k-order(θ,ϕ)-derivation of weightλ∈R.AR-linear mapD:L→Lis called a k-order generalized(θ,ϕ)-derivation of weightλwith respect toαif

for allx,y,z∈L,λ∈R.δ=±1.

Remark 2.6Ifλ=0 andδ=1,a k-order generalized(θ,ϕ)-derivation of weightλwith respect toαis called a generalized(θ,ϕ)-derivation with respect toα(see[16]-[17]).

Definition 2.7Letα:L→Lbe a k-order Jordan triple(θ,ϕ)-derivation of weightλ∈R.AR-linear mapD:L→Lis called a k-order generalized Jordan triple(θ,ϕ)-derivation of weightλwith respect toαif

for allx,y∈L,λ∈R.δ=±1.

Remark 2.8Ifλ=0 andδ=1,a k-order generalized Jordan triple(θ,ϕ)-derivation of weightλwith respect toαis called a generalized Jordan triple(θ,ϕ)-derivation with respect toα(see[16,17]).

Throughout this paperθ,ϕ,D,α:L−→LareR-linear maps and(λ,k):L×Lis a map defined by

for allx,y,z∈L,λ∈R.

Proposition 2.9LetRbe a 3-torsion free ring and letLbe aδJordan-Lie triple system over ringR.LetD:L→Lbe a k-order generalized Jordan triple(θ,ϕ)-derivation of weightλwith respect toα,whereαis a k-order Jordan triple(θ,ϕ)-derivation of weightλ.If

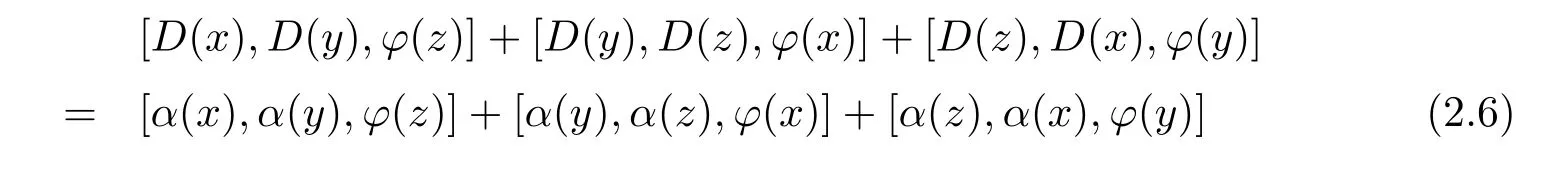
for allx,y,z∈L,then

for allx,y,z∈L,whereB(λ,k)=(λ,k)−(λ,k).

ProofBy(2.2)and(2.4),we have

for allx,y∈L.From(1.3),we have

for allx,y∈L.Since[x,y,x]+[y,x,x]+[x,x,y]=0,by(2.6)we have

for allx,y∈L.

We denoteT(x,y,z):=λ(δk[D(x),D(y),ϕ(z)]−δk[α(x),α(y),ϕ(z)]).Obviously,the mapT:L×L×L−→Lis R-trilinear.By(2.6),we have

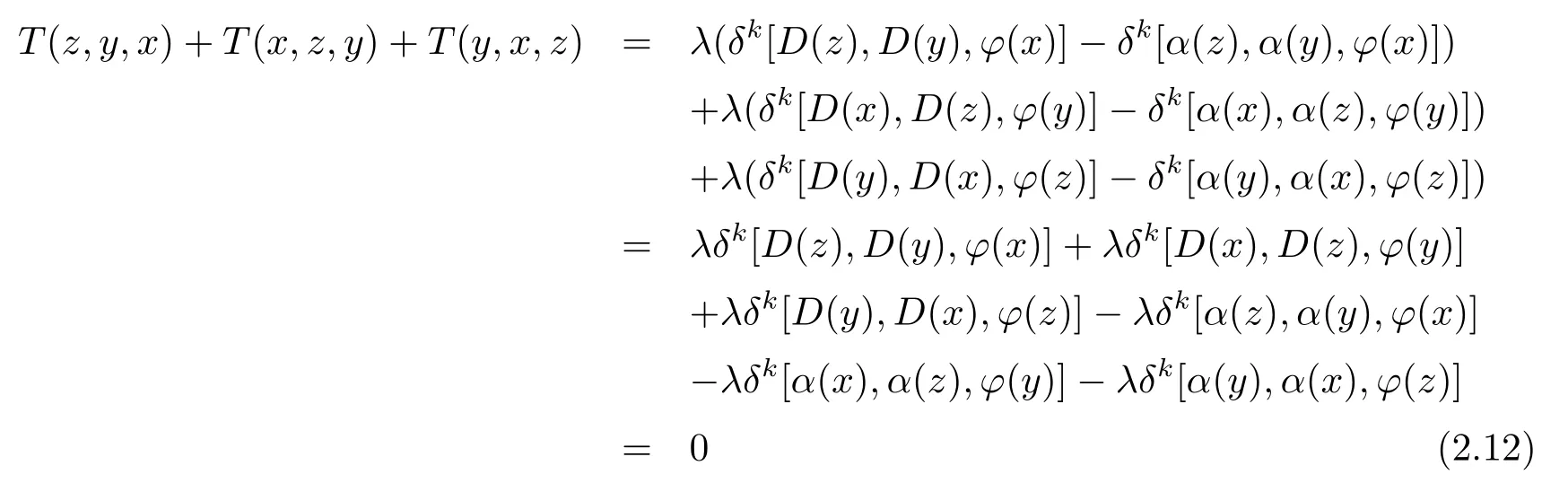
for allx,y,z∈L.It follows(2.9)that

for allx,y,z∈L.That is

for allx,y,z∈L.Thus,by(2.9)

Since

similarly by(2.11),we have

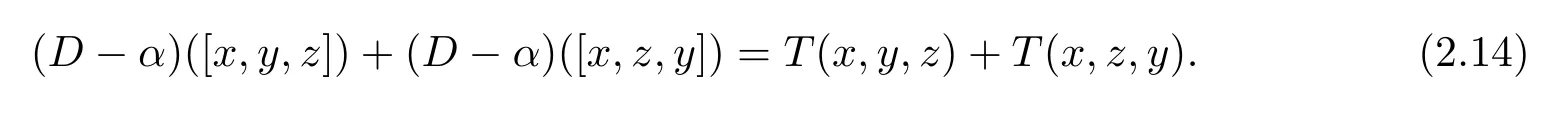
And by(2.10),we have

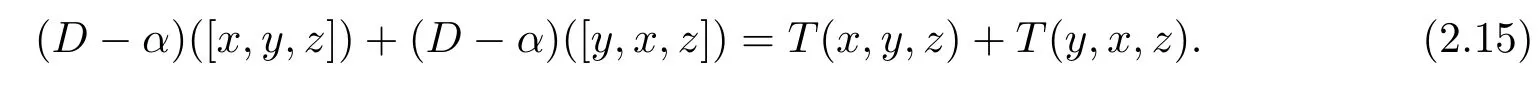
From(2.13),(2.14),(2.15),we have

for allx,y,z∈L.From(1.4)and(2.12),we obtain

SinceRis a 3-torsion free ring,

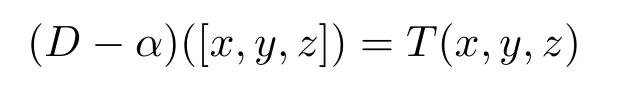
for allx,y,z∈L.This proves(2.7).

To prove(2.8),from(2.7)we have

Then

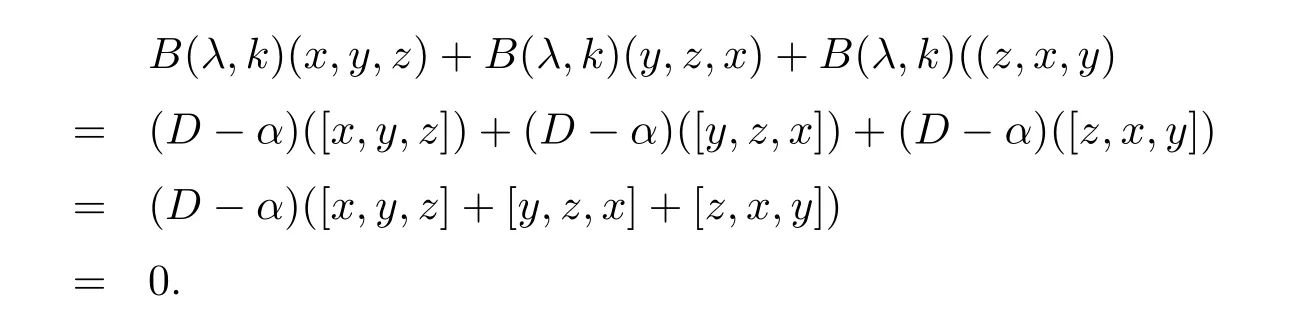
Proposition 2.10IfD:Lis a k-order generalized Jordan triple(θ,ϕ)-derivation of weightλwith respect toαsatisfying(2.7),whereαis a k-order Jordan triple(θ,ϕ)-derivation of weightλ,then(2.6)holds.

ProofIfλ=0,thenD([x,y,x])=α([x,y,x]).By(1.3)and(1.4)

Using the same method in Proposition 2.9,we have

for allx,y,z∈L.Therefore,(2.6)holds.Ifλ/=0,By(1.4)and(2.7),we have

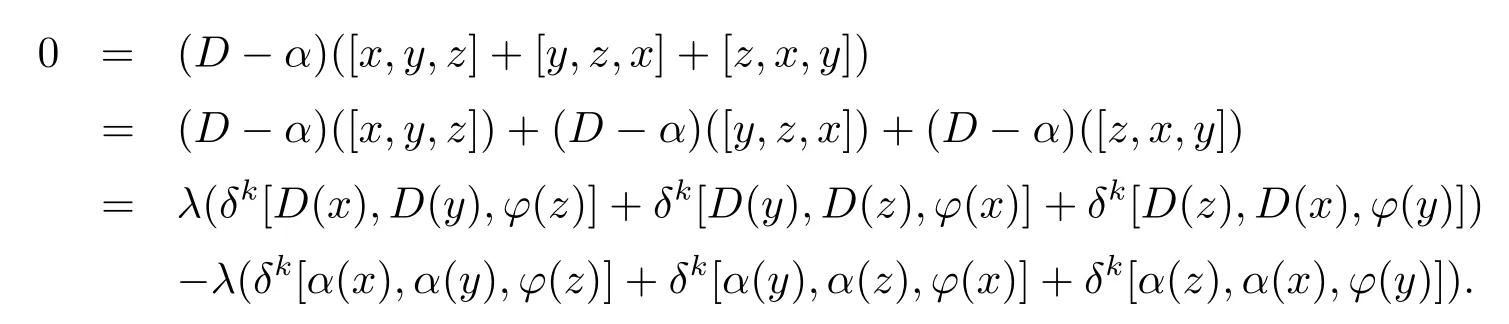
So,we obtain that

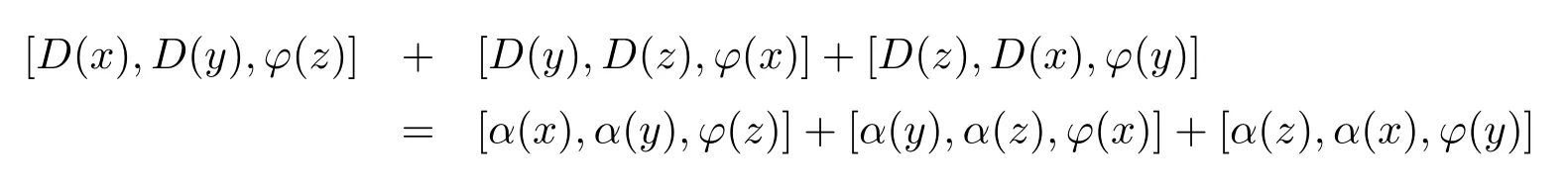
for allx,y,z∈L.

Theorem 2.11LetRbe a 3-torsion free ring and letD:L−→Lbe a k-order Jordan triple(θ,ϕ)-derivation of weightλ.ThenDis a k-order(θ,ϕ)-derivation of weightλif only if

for allx,y,z∈L.

ProofSupposeDis a k-order(θ,ϕ)-derivation of weightλ.On the one hand,

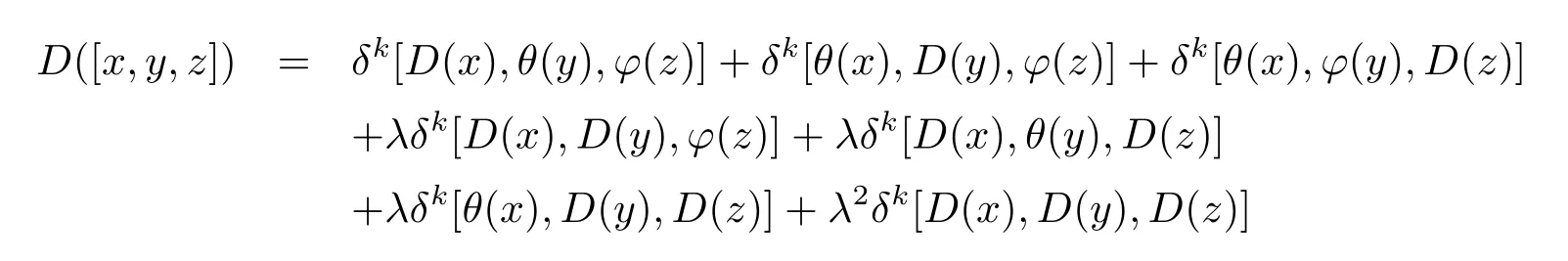
for allx,y,z∈L.On the other hand,

for allx,y,z∈L.Therefore,[θ(x),ϕ(y),D(z)]=[ϕ(x),θ(y),D(z)]for allx,y,z∈L.This proves(2.16).

This proves(2.17).

Conversely,we prove thatDis a k-order(θ,ϕ)-derivation of weightλif(2.16)and(2.17)hold.SinceDis a k-order Jordan triple(θ,ϕ)-derivation of weightλ,and by(1.3)and(2.16),we have

for allx,y,z∈L.By(1.4)and(2.17),we have

Using the same proof method as Proposition 2.9,we get

for allx,y,z∈L.

Thus,Dis a k-order(θ,ϕ)-derivation of weightλonL.

Theorem 2.12LetRbe a 3-torsion free ring and letD:Lbe a k-order generalized Jordan triple(θ,ϕ)-derivation of weightλwith respect to the k-order Jordan triple(θ,ϕ)-derivationαof weightλsatisfying(2.6).If

for allx,y,z∈L,thenαis a k-order(θ,ϕ)-derivation of weightλandDis a k-order generalized(θ,ϕ)-derivation of weightλwith respect toα.

ProofIt follows from Theorem 2.11 thatαis a k-order(θ,ϕ)-derivation of weightλ.

Applying Proposition 2.9,we get from(2.6)that

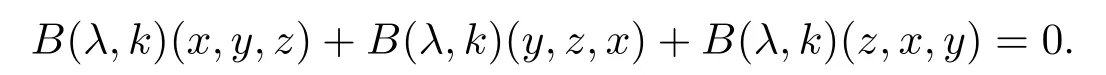
Then by(2.19),we have

for allx,y,z∈L.The rest of the proof is similar to the proof of Theorem 2.11.

Corollary 2.13LetRbe a 3-torsion free ring and letD:L−→Lbe a k-order generalized Jordan tripleθ-derivation of weightλwith respect to the k-order Jordan tripleθ-derivationαof weightλsatisfying(2.6).Thenαis a k-orderθ-derivation of weightλandDis a k-order generalizedθ-derivation of weightλwith respect toα.

ProofIt is clear that condition(2.18)of Theorem 2.12 is valid whenθ=ϕ.For condition(2.19)of Theorem 2.12,we have from(1.4)that

So condition(2.19)of Theorem 2.12 is valid ifϕ=θ.Henceαis a k-orderθ-derivation of weightλandDis a k-order generalizedθ-derivation of weightλwith respect toα.

Corollary 2.14LetRbe a 3-torsion free ring.ThenD:is a k-order Jordan tripleθ-derivation of weightλif and only ifDis a k-orderθ-derivation of weightλ.

ProofIt is clear that condition(2.6)of Corollary 2.13 is valid whenD=α.

Corollary 2.15LetRbe a 3-torsion free ring.ThenD:is a k-order Jordan triple derivation of weightλif and only ifDis a k-order derivation of weightλ.

ProofThis is a special case thatθ=ILin Corollary 2.14,whereILis the identity map onL.

Theorem 2.16LetLbe aδJordan-Lie triple system.LetD:LLbe a k-order(θ,ϕ)-derivation of weightλandAbe a linear automorphism ofL.IfA,θandϕsatisfy any two of which are commutative,thenADA−1is also a k-order(θ,ϕ)-derivation of weightλ.

ProofSinceDis a k-order(θ,ϕ)-derivation of weightλand we have

for allx,y,z∈L.SinceAis a linear automorphism ofL,we have

for allx,y,z∈L.Therefore,

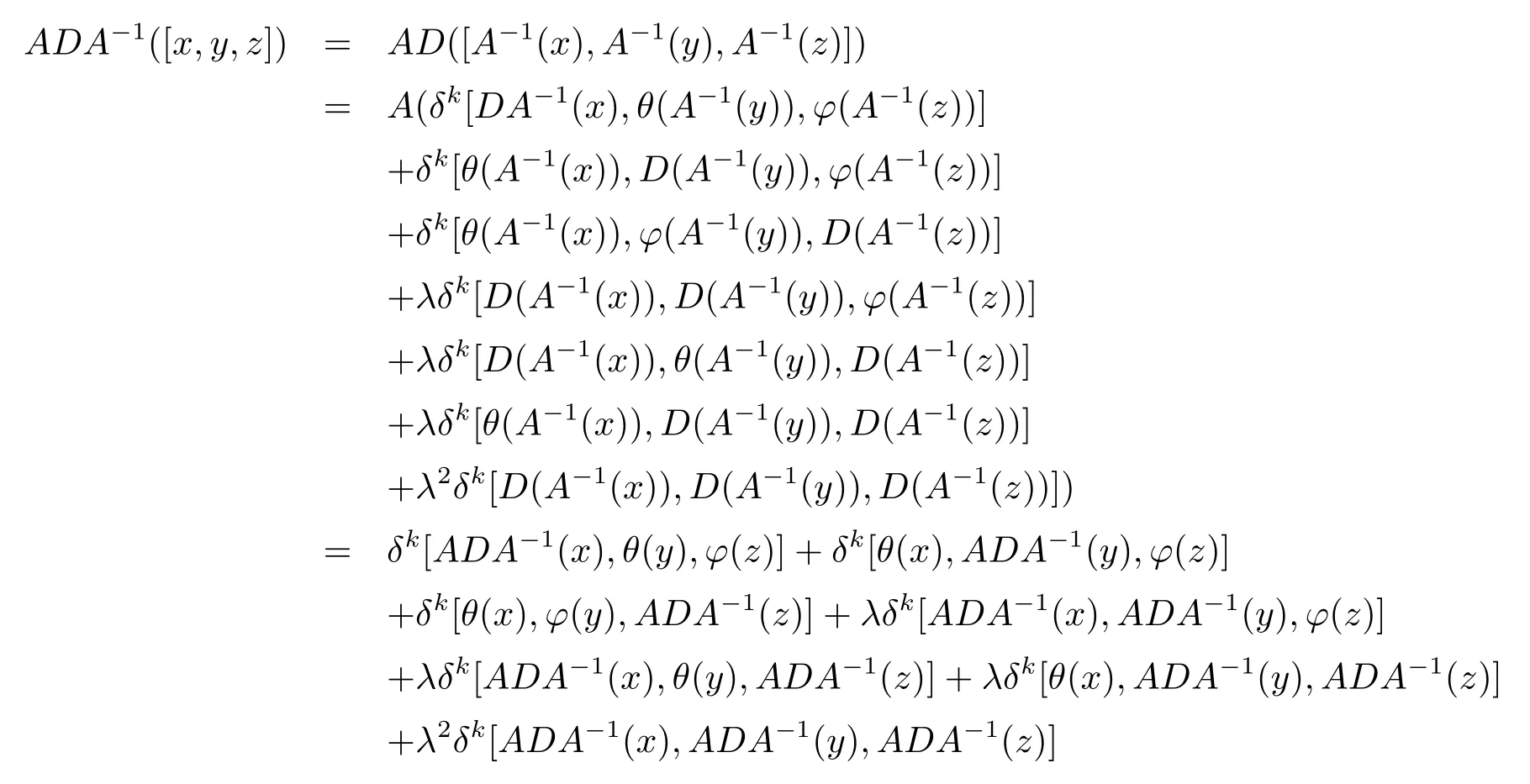
for allx,y,z∈L.SoADA−1is a k-order(θ,ϕ)-derivation of weightλonL.

Corollary 2.17LetRbe a 3-torsion free ring.LetAbe a linear automorphism ofL.ThenD:LLis a k-order Jordan triple derivation of weightλif and only ifAnDA−nis a k-order derivation of weightλfor all positive integern.

ProofIfDis a k-order Jordan triple derivation of weightλ,it follows Corollary 2.15 thatDis a k-order derivation of weightλ.And from Theorem 2.16,ADA−1is also a korder derivation of weightλ.By mathematical induction,AnDA−nis a k-order derivation of weightλfor all positive integern.Conversely,we prove thatDis a k-order Jordan triple derivation of weightλifAnDA−nis a k-order derivation of weightλfor all positive integern.Clearly,A−nis a linear automorphism ofLand from Theorem 2.16,A−nAnDA−nAn=Dis a k-order derivation of weightλ.Therefore,Dis a k-order Jordan triple derivation of weightλ.

Theorem 2.18IfDis a k-order derivation ofδJordan-Lie triple systemL,Z(L)is the center ofL,thenD(Z(L))⊆Z(L).

ProofFor arbitrary elementxinZ(L)and for ally,z∈L,we have[x,y,z]=0.SinceDis a k-order derivation,we have

Therefore,

for ally,z∈L.That isD(Z(L))⊆Z(L).

3 On K-Order Generalized Derivation of Weight λ on Rota-Baxter δ Jordan-Lie Triple Systems of Weight λ

In this section, firstly,we introduce the concepts of a Rota-BaxterδJordan-Lie algebra of weightλand a Rota-BaxterδJordan-Lie triple system of weightλ.Afterwards,we associate some beautiful results in section 2 with the inheritance property in[18]on a Rota-BaxterδJordan-Lie triple system of weightλ.In the end,we obtain that every Rota-BaxterδJordan-Lie algebra can be seen as a Rota-BaxterδJordan-Lie triple system.

Definition 3.1A Rota-BaxterδJordan-Lie algebra of weightλis aδJordan-Lie algebra(L,[·,·])with aR-trilinear mapp:LLsuch that

for allx,y∈L.Dis called k-order derivation of weightλon it if

for allx,y∈L.

Definition 3.2A Rota-BaxterδJordan-Lie triple system of weightλis aδJordan-Lie triple system(L,[,,])with aR-trilinear mapp:such that

for allx,y,z∈L.Furthermore,we callpis a Rota-Baxter operator of weightλonL.

Let(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλ.We define a ternary operation onLby

for allx,y,z∈L(see[12]).

Theorem 3.3Let(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλandTbe a invertible linear map.ThenTis a Rota-Baxter operator of weightλif and only ifT−1is a 0-order derivation of weightλ.

ProofSinceTis a invertible linear map,then for anyxi∈L(i=1,2,3),there existsyi∈L(i=1,2,3)such thatxi=Tyi(i=1,2,3).SupposeTis a Rota-Baxter operator of weightλ,then we have

for allxi∈L(i=1,2,3).Thus,T−1is a 0-order derivation of weightλ.Conversely,supposeTis a 0-order derivation of weightλ.Similarly,for allxi∈L(i=1,2,3),we have

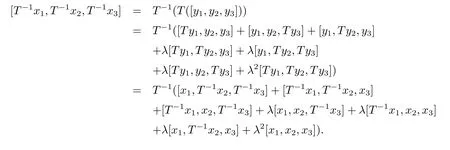
Therefore,T−1is a Rota-Baxter operator of weightλ.

Remark 3.4Obviously,the conclusion of Theorem 3.3 still holds on Rota-BaxterδJordan-Lie algebra of weightλ.

Theorem 3.5Let(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλ.Then(L,[,,]p,p)is a Rota-BaxterδJordan-Lie triple system of weightλ.

ProofFirst of all,we need to prove(L,[,,]p,p)is aδJordan-Lie triple system.Clearly,[,,]pdefined in(3.2)is multi-linear and we observe that

for allx,y,z∈L.Therefore,[,,]psatisfies(1.3).It follows from(1.4)that

for allx,y,z∈L.Therefore,[,,]psatisfies(1.4).To prove that[,,]psatisfies(1.5),we need to show

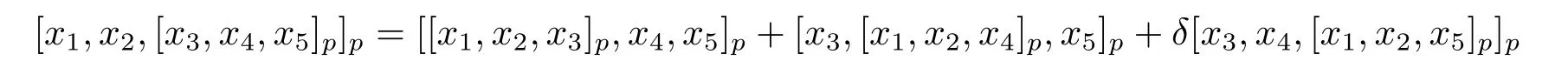
for allxi∈L(i=1,2,3,4,5).We notice that

for allx,y,z∈L.

Similarly,we can computeB:=[[x1,x2,x3]p,x4,x5]p,C:=[x3,[x1,x2,x4]p,x5]p,D:=[x3,x4,[x1,x2,x5]p]p.

It follows(1.5)that

Therefore,[,,]psatisfies(1.5).Then(L,[,,]p,p)is aδJordan-Lie triple system.Finally,we show thatpsatisfies(3.1)on(L,[,,]p,p).From the definition of[,,]p,we have

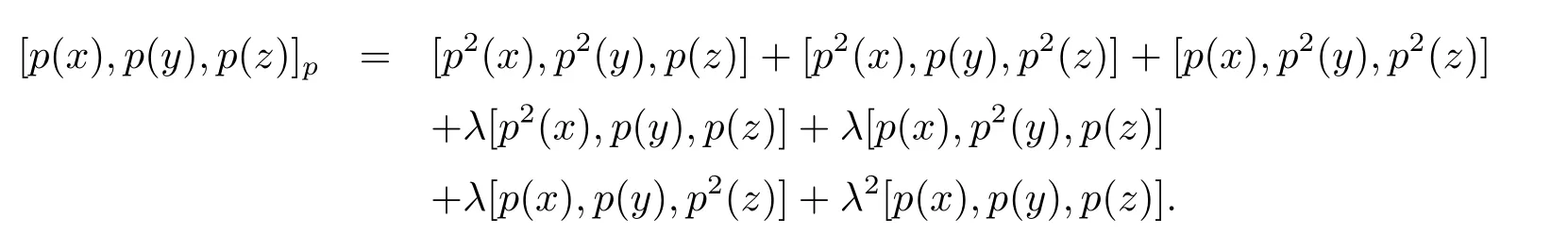
Sincepis a Rota-Baxter operator of weightλon(L,[,,],p),we have

By computing,we have

for allx,y,z∈L.This provespis a Rota-Baxter operator of weightλon(L,[,,]p,p).

Thus from the above sum,we conclude that(L,[,,]p,p)is a Rota-BaxterδJordan-Lie triple system of weightλ.

Theorem 3.6Let(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλ.LetDbe a k-order generalized(θ,ϕ)-derivation of weightλwith respect toαonLsatisfying the relation that any two ofD,p,α,θ,ϕare commutative.ThenDis a k-order generalized(θ,ϕ)-derivation of weightλwith respect toαon the Rota-BaxterδJordan-Lie triple system of weightλ(L,[,,]p,p),whereαis a k-order(θ,ϕ)-derivation of weightλ.

ProofWe have

It is a straightforward computation.By(3.3)-(3.9),we obtain

Therefore,Dis a k-order generalized(θ,ϕ)-derivation of weightλwith respect toαon the Rota-BaxterδJordan-Lie triple system of weightλ(L,[,,]p,p).

Corollary 3.7Let(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλ.LetDbe a k-order(θ,ϕ)-derivation of weightλonLsatisfying the relation any two ofD,p,α,θ,ϕare commutative.ThenDis a k-order(θ,ϕ)-derivation of weightλon the Rota-BaxterδJordan-Lie triple system of weightλ(L,[,,]p,p).

ProofIt is the direct results of Theorem 3.6.

Corollary 3.8Let(L,[,,])be aδJordan-Lie triple system.dis a invertible 0-order derivation of weightλonL,then(L,[,,]d−1)with[,,]defined in(3.2)is also aδJordan-Lie triple system.Furthermore

for allx,y,z∈L.dis a 0-order derivation of weightλon(L,[,,]d−1).

ProofBy Theorem 3.3,d−1is a Rota-Baxter operator of weightλon(L,[,,]).And by Theorem 3.5,(L,[,,]d−1)is aδJordan-Lie triple system.From Corollary 3.7,dis a 0-order derivation of weightλon(L,[,,]d−1).Thus,d−1is a Rota-Baxter operator of weightλon(L,[,,]d−1).Clearly,we have

for allx,y,z∈L.

Theorem 3.9Let(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλandAbe a linear automorphism on(L,[,,],p).IfAandpare commutative,thenAis also a linear automorphism on(L,[,,]p,p),where[,,]pis defined as(3.2).

ProofWe need to certifyA([x,y,z]p)=[A(x),A(y),A(z)]p,for allx,y,z∈L.From the definition of(L,[,,]p,p),we have

SoAis also a linear automorphism on(L,[,,]p,p).

Corollary 3.10Let(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλ.LetDbe a k-order Jordan tripleθ-derivation of weightλon(L,[,,],p)andAbe a linear automorphism of(L,[,,],p).IfA,p,θ,Dsatisfy the relation any two of which are commutative,thenAnDA−nis a k-orderθ-derivation of weightλon(L,[,,]p,p)for all positive integern,where[,,]pis defined as(3.2).

ProofSinceDis a k-order Jordan tripleθ-derivation of weightλon(L,[,,],p),and from Corollary 2.15,we have thatDis a k-orderθ-derivation of weightλon(L,[,,],p).From Corollary 3.7,Dis a k-orderθ-derivation of weightλon(L,[,,]p,p).SinceAis a linear automorphism of(L,[,,],p),and from Theorem 3.9,we know thatAis a linear automorphism of(L,[,,]p,p),and from Theorem 2.17,ADA−1is a k-orderθ-derivation of weightλon(L,[,,]p,p).By mathematical induction,AnDA−nis a k-orderθ-derivation of weightλon(L,[,,]p,p)for all positive integern.

Theorem 3.11Let(L,[·,·])be aδJordan-Lie algebra andDbe a 0-order derivation of weightλon it.ThenDis also a 0-order derivation of weightλonδJordan-Lie triple system(L,[,,]),where[,,]is defined by[x,y,z]:=[[x,y],z]]for allx,y,z∈L.

ProofSupposeDis a 0-order derivation of weightλon(L,[·,·]),then

for allx,y,z∈L.

Therefore,Dis also a 0-order derivation of weightλon(L,[,,]).

Corollary 3.12Let(L,[·,·],p)be a Rota-BaxterδJordan-Lie algebra of weightλ.Then(L,[,,],p)be a Rota-BaxterδJordan-Lie triple system of weightλ,where we assumepis invertible and[,,]is defined as above.

ProofIt just need to prove thatpis a Rota-Baxter operator of weightλon(L,[,,],p).By Remark 3.4,p−1is a 0-order derivation of weightλon(L,[·,·],p).From Theorem 3.11,p−1is a 0-order derivation of weightλon(L,[,,],p).By Theorem 3.3,we obtain thatpis a Rota-Baxter operator of weightλon(L,[,,],p).

Remark 3.13Actually,the conclusion of Corollary 3.12 still holds whenpis not invertible.It just need to use the same proof method as Theorem 3.11 to prove thatpis a Rota-Baxter operator of weightλon(L,[,,],p).