一类具有非线性传染率和治愈率的SIR模型的行波解

安阳学院数理学院 河南 安阳 455000

1 引言

医疗措施是实际传染病防治中阻止和控制疾病传播的有效方法．下面我们考虑一类具有治愈函数的传染病模型,其中疾病发生率和治愈函数分别为具体我们考虑下面的SIR模型

其中b表示易感染者和移出者的自然出生率及死亡率．δ表示染病者的死亡率及出生率．γ表示染病者的自然恢复率．q为垂直传染率,且p＝1－q．S和R的新生儿为易感染者,并且I的新生儿中未被垂直传染的那部分也为易感染者．以上参数均为正数．疾病的发生率是一个非线性函数,β为正常数,用来描述疾病的感染率,α是半饱和常数,且α≥0．非线性项,k＞0,μ≥0为饱和治愈函数,其中k表示治愈率,μ用来衡量染病者由于延迟治疗而导致治愈效果受影响的效应,在这里我们假设μ≤1．d1,d2,d3为扩散系数．

对于该模型,我们给出以下假设

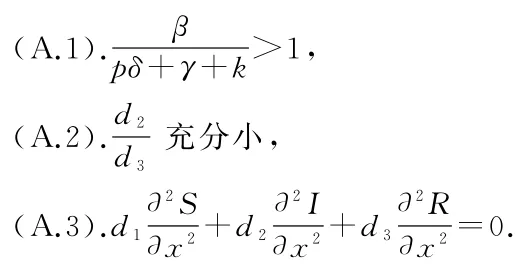
下面我们将证明,在(A．1)、(A．2)、(A．3)条件下,(1．1)具有连接从无病平衡点到地方病平衡点的行波解．

2 行波解的存在性

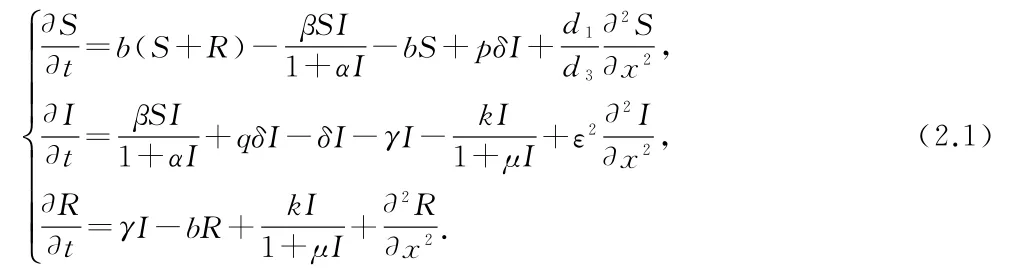
把 (1．1) 三 个 方 程 相 加, 得 到由 (A．3),可进一步得到在该假设下,总人口N是一个常数,为方便起见,不妨再假定N＝1,这样一来S,I和R就变成了易感染者、染病者和移出者各自在总人口中所占的比例．通过变换S＝1－I－R,系统 (2．1)的后两个方程就不再包含S．因此系统 (2．1)等价于下面的2维系统

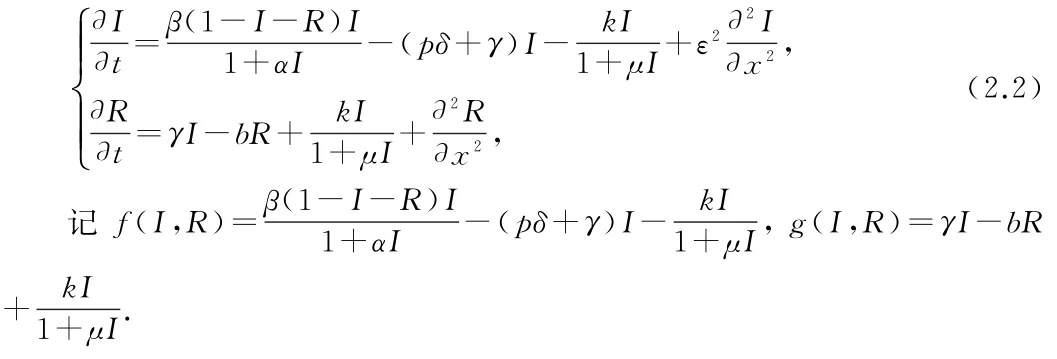
显然,(2．2)始终有一个无病平衡点E0(0,0)．并且,如果满足条件(A．1),则由下面的方程

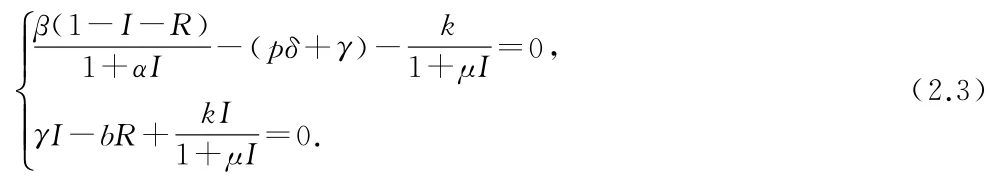
可以解得(2．2)还存在唯一的地方病平衡点E∗＝(I∗,R∗),其中

接下来,我们使用[1]中的方法证明 (2．2)具有连接 平衡点E0和E∗的行波解．

3 对结论的一些说明