基于课堂学习数据的期末成绩预测方法的研究①

覃斌毅 李芸

摘要：在高校教学活动中，学生期末考试成绩是评估学生对所学知识掌握程度的重要依据，也是评价教学质量的重要指标之一。学生在课程学习中的学习行为与期末考试成绩存在着一种量化关系。本文使用雨课堂对课程学习数据进行采集，然后使用主成分分析方法对数据进行分析，并通过混淆矩阵评价成绩预测结果，最终实现通过平时课堂学习数据预测课程期末成绩。

关键词：雨课堂主成分分析成绩预测混淆矩阵

Abstract： In college teaching activities， students' final examination results are not only an important basis for evaluating students' mastery of knowledge， but also one of the important indicators for evaluating teaching quality.There is a quantitative relationship between students' learning behavior in course learning and their final exam scores. In this paper， the rain classroom is used to collect the course learning data， then the principal component analysis method is used to analyze the data， and the score prediction results are evaluated through the confusion matrix. Finally， the final score of the course is predicted through the usual classroom learning data.

Key Words： Rain classroom; Principal component analysis; Performance prediction; Confusion matrix

《教育信息化十年发展规划（2011-2020年）》中提出“推动信息技术和高等教育的合理融合，利用信息化工具和平台提升教学水平”。在高校教学活动中，学生期末考试成绩是评估学生对所学知识掌握程度的重要依据，也是评价教学质量的重要指标之一。研究表明，学生在课程学习中的学习行为与期末考试成绩存在着一种量化关系。通过这种量化关系，可以根据学生在课程中的学习行为，预测出学生期末考试是否会挂科，使得教师在教学过程中及时对存在挂科风险的学生进行指导，避免挂科，从而提高教学质量。如何利用信息化工具，记录下学生在课程学习中的学习行为数据，并对数据进行分析，得出学习行为与课程期末考试成绩的联系，建立期末成绩预测模型，具有实际应用价值。

在国外，Shaymaa E.Sorour等[1]人通过分析学生的课程评论数据，提取出评论属性，然后利用决策树和随机森林算法预测学生课程成绩。Agoritsa Polyzou等[2]人利用线性回归和矩阵因子分解对学生个人已修课程成绩进行分析，进而对学生未修课程的成绩进行预测。美国普渡大学构建了课程信号系统[3]，该系统收集了学生过往学习的数据，借助该系统可以预测学生在学习某一门课程中是否存在危机，及时向存在危机风险的学生提出合理的建议，并选择合适的学习资源推送给学生，降低学习危机发生率。Juan A. Lara等[4]人建立了辍学学生和完成课程的学生的参考模型，该模型分析的数据来源于学生在Moodle学习平台学习时所形成的交互数据。

在国内，谢露露等[5]使用神经网络对MOOC上学生学习的数据进行分析，取得了较好的预测成绩结果。Liu等[6]从教学系统存储的学生日志数据中提取出所需的特征，并利用提取的特征作为分类器的输入，最终实现学生成绩的预测。暴延敏[7]大数据使用支持向量机对学生的个人综合数据进行建模，预测学生能否顺利毕业。陈秀玲[8]使用主成分分析法对教务系统中收集到的教务数据进行分析，得出毕业学生综合成绩评定排名。贾靖怡等[9]建立了基于Adaboost算法的MOOC学习者徐向成绩预测模型。黎龙珍[10]借助数据预处理方法和决策树C4.5，对收集到在线学习的高维行为特征数据进行分析，建立了成绩预测模型。

当前对课程成绩预测的研究主要分析的是线上教学或特定的学生系统上的数据，对线下课堂教学的数据分析较少。与线上教学不同，传统的线下教学数据往往不易于收集。然而，线下教学仍是高校当前进行教学活动的主要形式。因此，如何收集并利用好线下教学的数据尤为重要，雨课堂就是一种很好的收集线下教学数据的教学工具。

在2016年，清华大学推出一款智慧教学工具—雨课堂。它将信息技术融入到课程教学中，在后臺对教学大数据进行“全景式”记录，为整个教学过程提供数据化、智能化的信息支持。它的运行方式是通过增强微信和PPT这两个常用软件的功能，实现了课堂教学数据的采集[11][12]。

因此，本文提出借助雨课堂对课程学习数据进行采集，然后使用主成分分析方法对数据进行分析，并通过混淆矩阵评价成绩预测结果，最终实现通过平时课堂学习数据预测课程期末成绩。

1 主成分分析介绍

主成分分析（Principal Component Analysis，PCA）是统计学中的一种多元统计分析方法。它是通过将原始数据的多个变量通过线性变换，以选出较少个数重要变量。这些选出的重要变量往往包含了原始数据变量所包含的重要信息。

主成分是按照方差贡献率的大小进行降序排序的，方差贡献率最大的主成分称为第1主成分，依次类推。

2 期末成绩预测

2.1 预测目标

本文以课程《传感器原理》为例，在该课程的教学过程中，使用雨课堂对学生课堂学习数据进行记录。然后，借助主成分分析方法对数据进行分析，预测学生能否通过该门课程期末考试。

2.2 数据来源

本次使用的课堂数据来源于2019年春季期和2018春季期《传感器原理》线下教学中使用雨课堂采集到的学生学习数据，2019春季期教学班为48人，2018春季期教学班为43人。其中，学生学习数据包括每个章节的课堂练习情况、到课次数、平时成绩等共10种变量。

2.3 代表性变量选取及合理性分析

在建模前，使用散点图、计算期末成绩与变量的相关系数结合的方法从10种变量中筛选出主成分分析需要的变量。

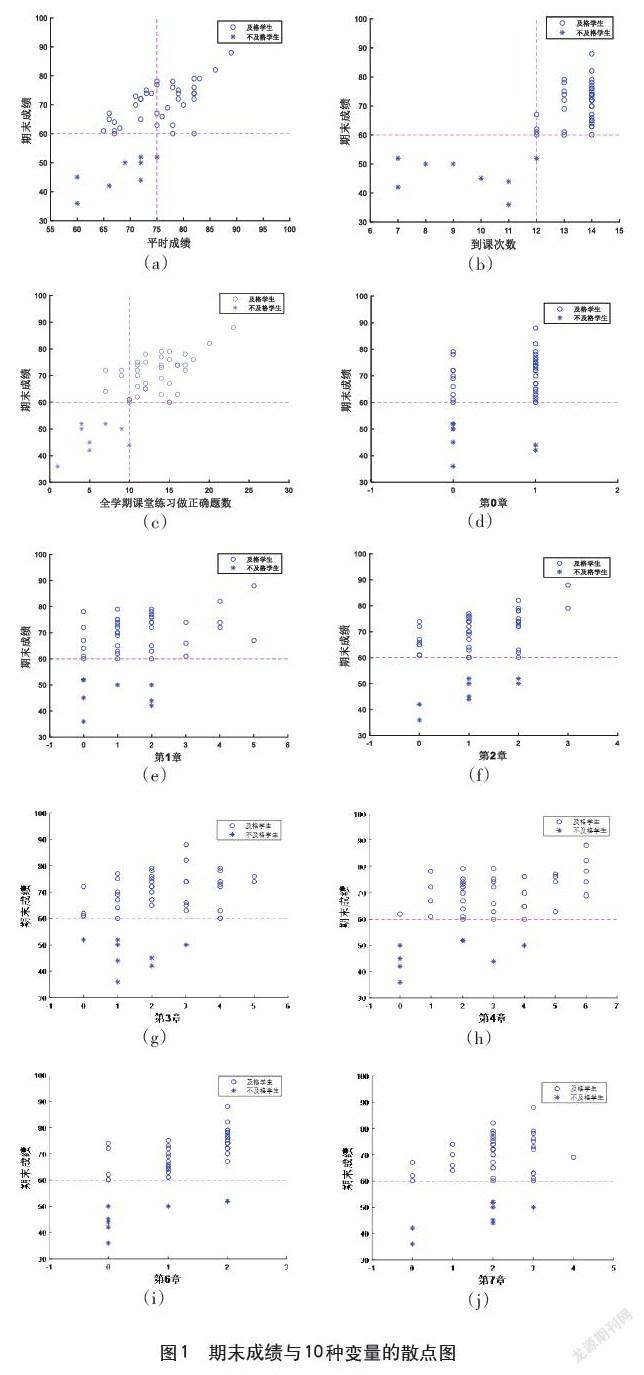
图1为10个变量与期末成绩的散点图。图1（a）反映了平时成绩与期末成绩的关系，其中平时成绩是由课堂表现、课后作业来构成。从图1（a）看到，以平时成绩75分为分界线，平时成绩大于75分的学生在期末考试均能通过;平时成绩低于75分的学生则有可能出不及格的情况，表明平时成绩与期末成绩呈现一定的相关性。

图1（b）反映了到课次数与期末成绩的关系。从图1（b）看到，以到课次数12次为分界线，到课次数大于12次的学生在期末考试均能通过;到课次数低于12次的学生期末考试均没能通过。这表明到课次数与期末成绩有较强的相关性。这是因为到课次数在一定程度上反映了学生对本门课程的重视程度，到课次数越低，说明学生对课程的重视程度越低，越容易导致挂科。

图1（c）显示的是全学期课堂练习正确题数与期末成绩的关系。从图1（c）看到，以正确题数10题为分界线，正确题数大于10道题的学生期末考试均能通过;正确题数低于10题的学生则可能出现不及格的情况，且随着正确题数的减少，不及格的可能性随之增大，表明全学期课堂练习正确题数与期末考试成绩有相关性。这是因为课堂练习在一定程度上反映了学生当堂掌握知识的程度，学生当堂掌握知识越好，越有利于后期考试。

图1（d）-图1（j）显示的是各个章节课堂练习正确题数与期末成绩的关系。除了图（f）第六章课堂练习正题数与期末成绩呈现相关性以外，其他章节与期末成绩没有呈现明显的相关性。这是因为期末考试涉及到各个章节的内容，学生单一章节的练习情况难以反映对整个课程知识的掌握情况。

综上所述，平时成绩、到课次数、全学期课堂练习正确题数、第6章课堂练习正确题数这4种变量与期末成绩相关性较强，可作为后续建模的备选变量。

为了进一步筛选出变量，分别计算期末成绩与平时成绩、到课次数、全学期课堂练习做正确题数、第六章课堂练习做正确题数的相关系数，并以0.65为阈值，确定选取的变量。经计算得出，期末成绩与平时成绩、到课次数、全学期课堂练习做正确题数、第六章课题练习做正确题数的相关系数分别为0.69、0.76、0.74、0.64。因此，最终选取平时成绩、到课次数、全学期课堂练习做正确题数为主成分分析的输入变量。

2.4 预测结果

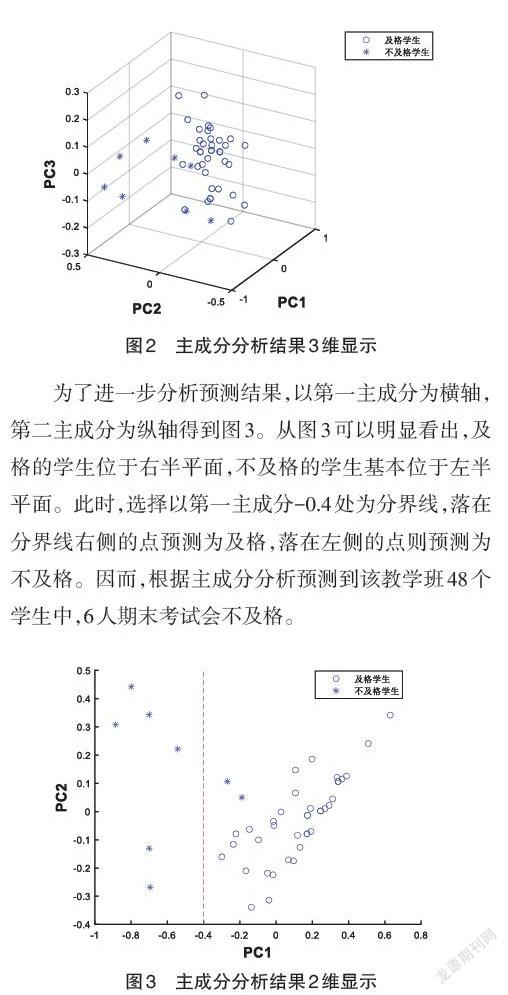
在使用PCA前，先对选取的3种变量分别进行归一化。然后，将归一化后的变量作为PCA的输入，以第一、第二、第三主成分作为坐标轴得到如图2所示。在图中，*表示期末不及格的学生，o表示期末及格的学生。从图2看到，及格的学生分布在右半空间，而不及格的学生分布在左半空间，它们具有较明显的区分度。

为了进一步分析预测结果，以第一主成分为横轴，第二主成分为纵轴得到图3。从图3可以明显看出，及格的学生位于右半平面，不及格的学生基本位于左半平面。此时，选择以第一主成分-0.4处为分界线，落在分界线右侧的点预测为及格，落在左侧的点则预测为不及格。因而，根据主成分分析预测到该教学班48个学生中，6人期末考试会不及格。

3 预测效果评价

3.1 运用混淆矩阵模型评价预测结果

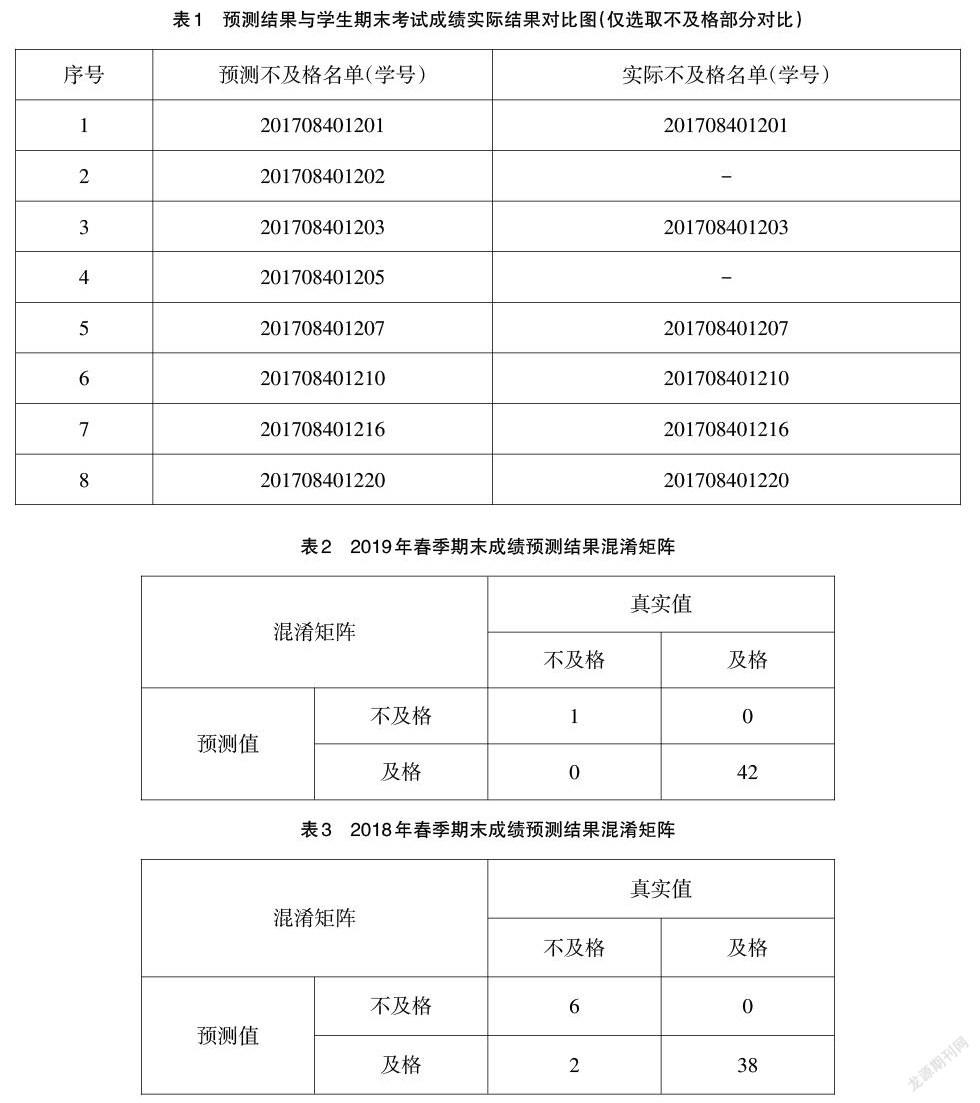
2019年春季期《传感器原理》学生期末考试成绩预测结果与学生期末考试成绩实际结果对比图（仅选取不及格部分对比）如表2所示。

根据表2，我们可以得到混淆矩阵如表3所示。

根据混淆矩阵，得到该模型的准确率为92%，召回率为75%，故模型具有较好的预测性能。

为了进一步验证所提方法的泛化能力，本文使用相同的分析方法，对《传感器原理》另一个班级2018年秋季期的期末成绩运用主成分分析法进行预测，并与期末考试实际结果对比，得到混淆矩阵如表4所示。

根据混淆矩阵，得到该模型的准确率为100%，召回率为100%，进一步表明该模型具有很好的预测性能。

4 结语

本文利用雨课堂对线下教学数据进行收集，然后使用主成分分析PCA对数据进行分析，最终得出学生是否能通过期末考试的预测。研究结果表明，借助PCA对线下教学数据分析，可以准确预测出学生期末考试的通过情况，有助于及时对预警学生进行干预，避免挂科，提高教学质量。

參考文献

[1] Sorour S E ， Mine T . Building an Interpretable Model of Predicting Student Performance Using Comment Data Mining[C]// Iiai International Congress on Advanced Applied Informatics. IEEE， 2016.

[2] Polyzou A ， Karypis G . Grade prediction with models specific to students and courses[J]. international journal of data science & analytics， 2016， 2（3-4）：1-13.

[3] 刘艳华，徐鵬.大数据教育应用研究综述及其典型案例解析——以美国普渡大学课程信号项目为例[J].软件导刊（教育技术），2014，13（12）：47-51.

[4] Jokhan A ， Sharma B ， Singh S . Early warning system as a predictor for student performance in higher education blended courses[J]. Studies in Higher Education， 2018：1-12.

[5] Li X ， Xie L ， Wang H . Grade Prediction in MOOCs[C]// 2016 IEEE Intl Conference on Computational Science and Engineering （CSE） and IEEE Intl Conference on Embedded and Ubiquitous Computing （EUC） and 15th Intl Symposium on Distributed Computing and Applications for Business Engineering （DCABES）. IEEE， 2016.

[6] Liu W ， Wu J ， Gao X ， et al. An early warning model of student achievement based on decision trees algorithm[C]// 2017 IEEE 6th International Conference on Teaching Assessment， and Learning for Engineering （TALE）. IEEE， 2017.

[7] 暴延敏. 基于大学生行为分析的学业预警方法研究[D].石家庄：河北师范大学，2018.

[8]陈秀玲.基于贝叶斯k近邻和主成分分析的教务数据挖掘研究[D].哈尔滨：哈尔滨工程大学，2007.

[9]贾靖怡，李玉斌，姚巧红，袁子涵.基于AdaBoost的MOOC学习成绩预测模型研究[J].软件导刊，2021，20（3）：242-246.

[10]黎龙珍.基于决策树算法的在线学习成绩预测[J].信息技术与信息化，2021（1）：130-133.

[11]王帅国.雨课堂：移动互联网与大数据背景下的智慧教学工具[J].现代教育技术，2017，27（5）：26-32.

[12]覃斌毅，李芸.基于Z管理图的学生学习效果定性分析方法研究[J].科技视界，2021（1）：46-48.