双调和算子组高阶谱的估计式

黄振明

(苏州市职业大学 数理部， 江苏 苏州 215104)

在描述弦振动、热传导等许多物理现象时，最终都会归结到包含调和算子Δ的微分方程或方程组的谱问题。由于不同问题的离散谱代表了诸如物体振动的频率、粒子运动的势能等实际意义，因此，谱问题一直是微分方程理论研究的重点内容。近年来，国内外众多学者采用各种方法，对各自研究领域中含基本算子Δ的微分方程(组)的谱问题进行讨论，取得了诸多的理论成果[1-11]。文献[1]讨论了双调和算子的谱问题(也称作clamped plate问题)：(Δ2+v)u=Γρu，其中v是所论空间上的有界连续函数，ρ>0是权函数，Γ是离散谱，并得到了估计谱的一个隐式不等式。尽管双调和算子的谱问题研究成为热点已有几十年的历史了，但未见有学者对双调和算子组的谱问题进行讨论。因此，在文献[1]研究成果的基础上，笔者尝试探讨如下双调和算子组的谱问题：

(1)

其中i=1,2,…,l(l为大于或等于1的整数)，Ω⊂Rm(m≥2)是一个边界逐片光滑的有界区域，v是边界∂Ω的单位外法向量，x=(x1,x2,…,xm)，常数aij=aji，函数bij(x)=bji(x)(i,j=1,2,…,l)，且满足对任意l维向量ξ=(ξ1,ξ2,…,ξl)T，成立

(2)

(3)

μ1≤ρ(x)≤μ2，

(4)

上述v1、v2、μ1、μ2均为正实数。为推导方便，将下列一组l阶对角算子矩阵记为R1()=diag[,,…,]，R1(Δ)=diag[Δ,Δ,…,Δ]，R2(Δ)=diag[Δ2,Δ2,…,Δ2]，l阶对称系数矩阵维函数列向量则可将问题(1)写成下列矩阵形式：

(5)

1 准备知识

(6)

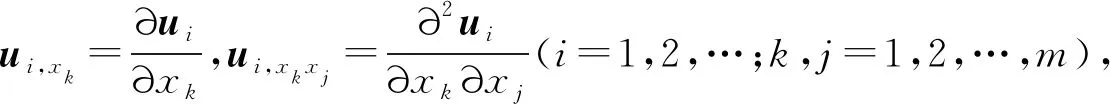
即有

(7)

(8)

利用算子Δ的运算性质，计算得

(9)

(10)

(11)

利用式(8)和(11)有

(12)

因为对i=1,2,…,n-1，成立Γi≤Γn，所以在式(12)中，用Γn替代所有的Γi(i=1,2,…,n-1)，有

(Γn+1-Γn)U≤4I。

(13)

2 引理

引理1 设ui是问题(5)对应谱Γi(i=1,2,…,n)的特征函数，则

(14)

证明利用分部积分、问题(5)的边界条件、Schwarz不等式和式(7)，得

即为引理1。

引理2 设ui是问题(5)对应谱Γi(i=1,2,…,n)的特征函数，则

证明利用分部积分，有

移项得

(15)

利用分部积分和式(2)，可得式(15)右端第二项

(16)

最后，利用式(2)、(15)、(16)和引理1，有

引理2得证。

引理3 对于I，有如下的估计上界

证明将φik的定义式代入Iik可得

由引理2得

引理3证毕。

引理4 对于U和Γi(i=1,2,…,n)，有下列不等式成立

证明由φik的定义，有

(17)

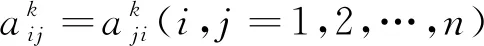
(18)

利用式(6)、(17)、(18)得

(19)

根据式(4)、Schwarz不等式和式(19)，有

(20)

最后，利用式(20)和引理1，得

化简即得引理4。

3 主要结果

定理1 设Γi(i=1,2,…,n+1)是问题(5)的前n+1个谱，则有高阶谱的显式估计式

(21)

(22)

证明利用引理3和引理4，从式(13)可得式(21)，在式(21)中用Γn来替代Γi(i=1,2,…,n-1)，即可得式(22)。

定理2 对于任意整数m≥2、n≥1，有谱的隐式估计不等式

证明选择参数σ>Γn，利用式(12)和U的定义，有

(23)

根据式(4)、(19)和Young不等式，有

(24)

(Γn+1-σ)U≤4I-V,

(25)

(26)

利用引理1和式(26)，有

(27)

(28)

根据式(27)和(28)，有

(29)

将式(29)和引理3中的估计式代入(25)，得

(30)

选取恰当的σ，使式(30)右端等于零，并用Γn+1替代其中的σ，化简即得定理2。

4 一般情形

将定理1、2的结论推广至如下任意阶调和算子组的离散谱问题

(31)

其中i=1,2,…,l,t≥2，且满足式(2)—(4)。采用与上述类似的讨论方法，通过推导，可得到问题(31)的离散谱与特征向量间的不等式关系，并最终推得如下的两个估计结论，证明在此省略。

定理3 设Γi(i=1,2,…,n+1)是问题(31)的离散谱，则有估计第n+1个谱Γn+1上界的显式不等式

定理4 对于问题(31)的第n+1个谱Γn+1，有下列隐式估计不等式

5 小结

笔者运用Rayleigh定理对问题(5)的高阶谱Γi(i为任意整数)进行讨论，得到用前n个谱来估计第n+1个谱上界的解析不等式，其估计系数与区域的度量无关。文献[1]讨论的问题恰是本文问题当l=1,a11=1时的特例，因此，本文结论是文献[1]结论的进一步推广，在力学和物理学中有更广的应用价值。