三相PWM 整流器输出调节子空间算法研究*
郭旭刚
(中国铁道科学研究院集团有限公司 机车车辆研究所,北京100081)
PWM 整流技术现已广泛应用于高铁牵引和辅助变流器系统中,在现有的PWM 整流器控制策略中,电流控制已经逐渐成熟,并得到推广应用,但是电流控制需要经过复杂算法进行控制,动态响应速度相对较慢.目前国内外很多学者把目光投向直接功率控制算法,直接功率控制仅需要进行简单的3/2 变换,无需调制模块,结构算法简单,动态响应快,低谐波,动态性能良好等优点[1−2]。
1 三相电压型PWM 整流器的数学模型
图1 为网侧变换器拓扑电路,该拓扑电路由交流回路、整流桥电路以及直流回路组成。其中交流回路包括交流电压E 及网侧电感L 等;直流回路包括电解电容和直流负载。
α−β静止坐标系下PWM 整流器数学模型:
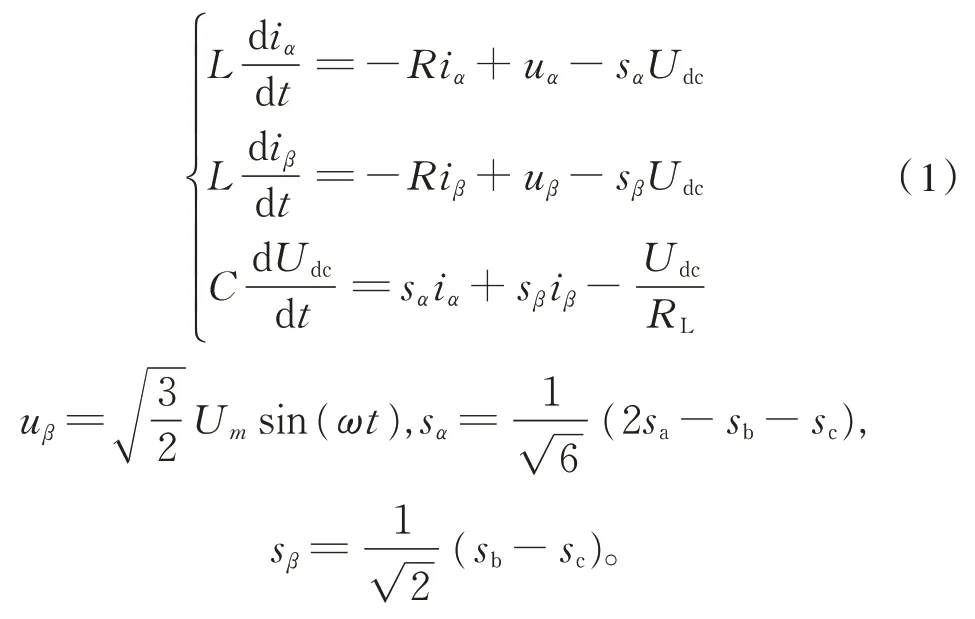
将 8 个开关矢量带入sα、sβ可得到α−β静止坐标系下的开关表如表1。
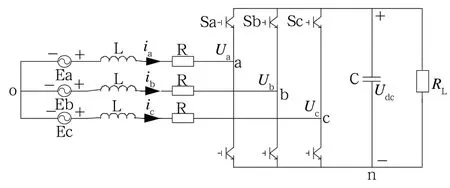
图1 三相电压型PWM 整流器基本电路图
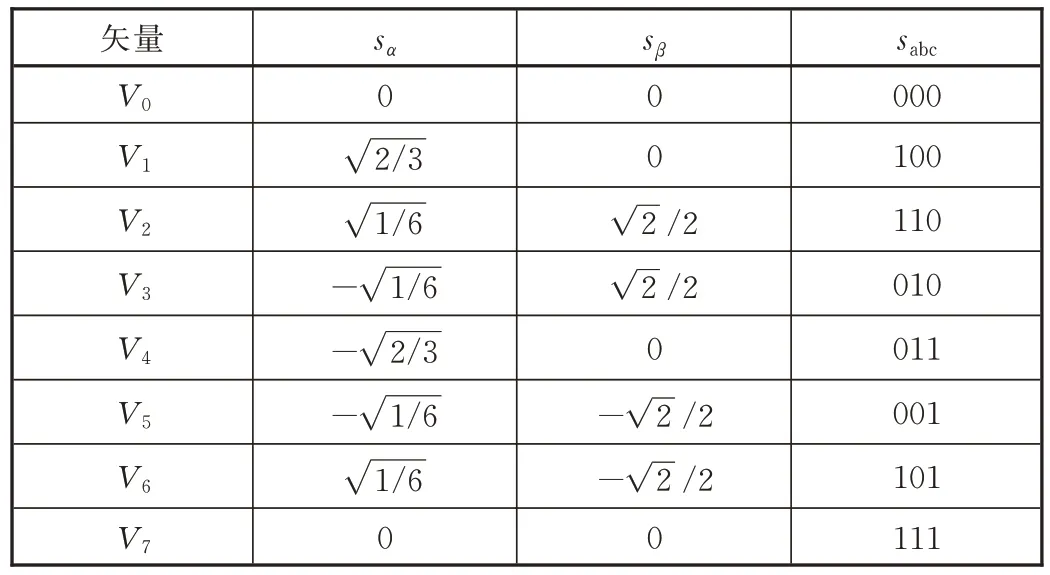
表1 两相静止标系下开关表
2 新模型下的直接功率控制系统图
三相电压型DPC 系统原理如图2 所示,主要由主电路(如图1)和控制电路组成。控制电路由直流电压平方外环和功率内环组成。
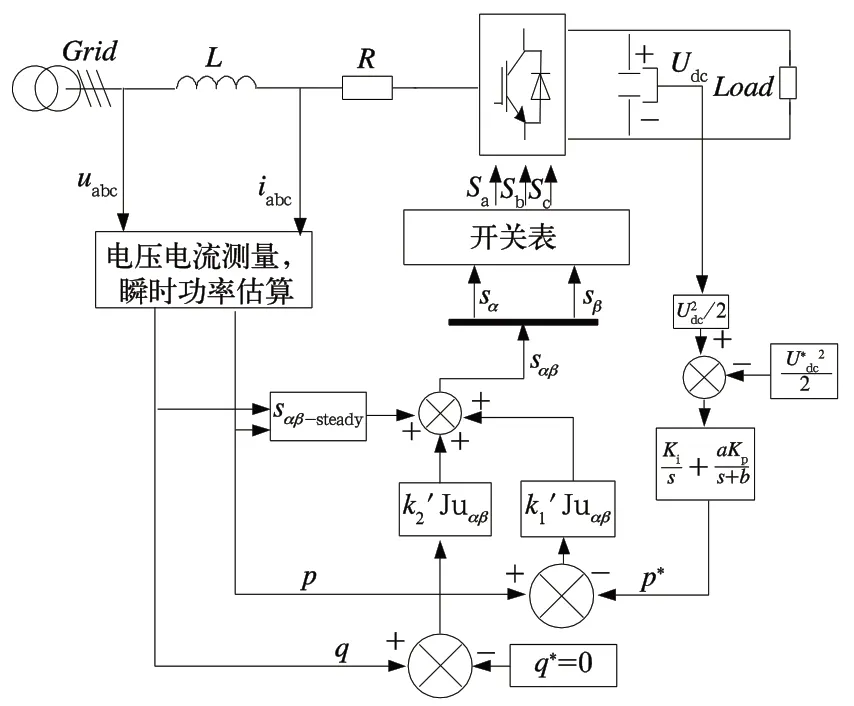
图2 基于ORS 的直接功率控制框图
基于ORS 的直接功率控制系统采用双闭环结构,内环为功率环,外环为电压环。内环将有功功率和无功功率的给定与实际估算量的偏差作为输入信号,配合开关矢量调节,选择相应的的开关量(IGBT 的导通信号),控制功率器件的开通与关断,进而控制输出量,外环主要是建立起与内环的联系,通过外环的输出产生内环有功功率的给定,给定量为直流电压偏差信号与实际测量电压的乘积。
采用电压平方外环和功率内环,提高了电压和功率的跟踪能力,系统响应特性较好较快,系统架构简单,抗负载干扰性能较好。
3 功率环设计及原理
通过瞬时功率理论可估算瞬时有功和无功功率的估计值p、q。
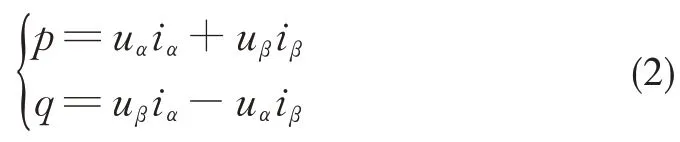
分别对瞬时有功功率、无功功率进行求导得到:
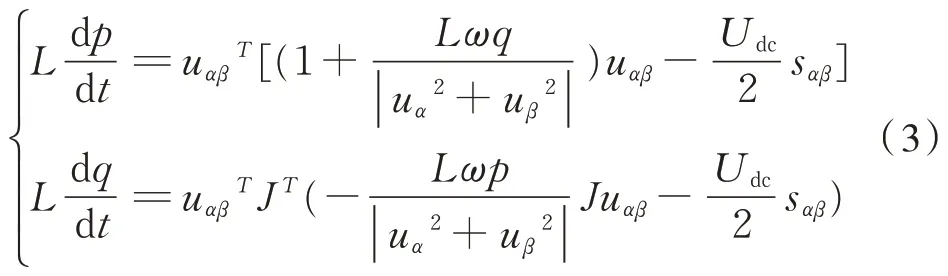
式(3)中形如xαβ,表示为xαβ=[xα xβ]T∈R2。
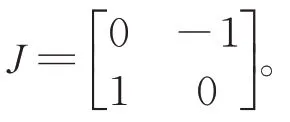
当 dp/dt、dq/dt分别为常数k1、k2时,由式(3)可以得到:
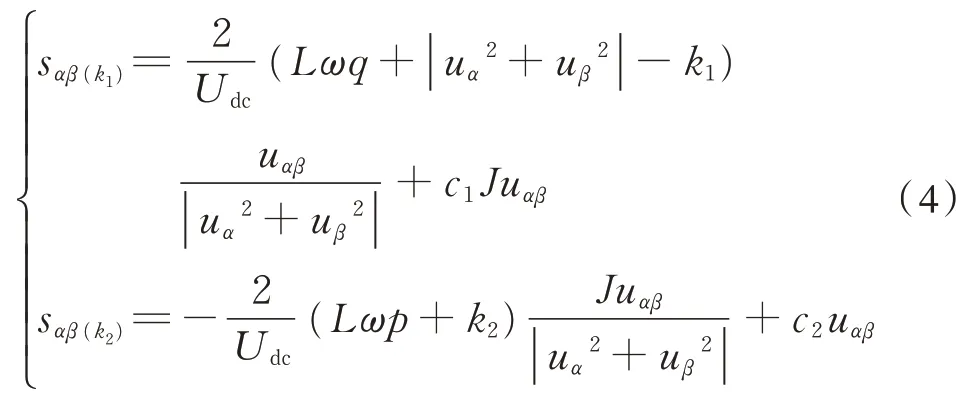
观察式(4)可以看出,sαβ(k1)、sαβ(k2)分别表示为两条互相垂直的直线(图 3 虚线箭头),其中c1Juαβ、c2uαβ分别用来表示直线的方向。sαβ(k1)直线表示选取矢量能使得dp/dt为一常数,sαβ(k2)直线表示选取矢量能使得 dq/dt为一常数。这样sαβ(k1)直线就把平面分为2 块区域,即dp/dt>k1或者 dp/dt<k1,同理sαβ(k2)。这样平面共分为了4 个区域,如图3。
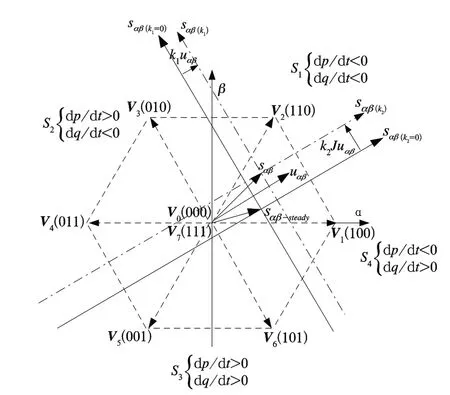
图 3 基于 ORS 的 S1~S4 区域划分
特别的,当k1=k2=0 时,表示有功和无功不再变化,且处于稳定状态。此时两条直线(实线箭头)将平面分为4 个区域S1~S4,交点为sαβ−steady(稳态状态)可由式(4)和sαβ(k1=0)、sαβ(k2=0)估算为:

系统正常运行时,对于开关矢量sαβ,系统可处于4个区域中任一位置,当处于任意位置时,通过图3 矢量合成可以调节到稳定位置,现以S1区域为例。
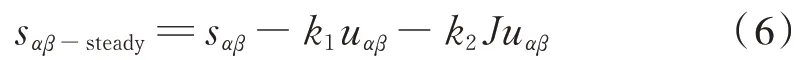
文中[3−5]讨论了功率误差与选择区域的关系,定义有功、无功功率误差分别为pe=p−p*、qe=q−q*,当功率误差大于或者小于0 时,通过选择不同区域的开关矢量对功率的作用来增减功率,即可得到表2。
控制系统通过对功率误差的估算,得到矢量所在区域,最后得到参考矢量对系统进行控制,即表3 关系。

表2 功率误差与区域划分的关系
从表 3 看出 ,可定义k1=k1′pe、k2=k2′qe,其中k1′、k2′为大于0 的常数,简化控制系统参数。则式(6)可表示为:
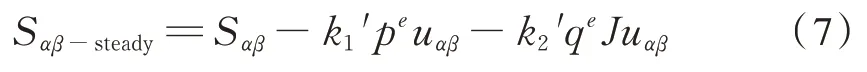
由式(7)可知,任意时刻不论系统运行于哪个区域,都可以通过控制得到稳定状态。

表3 功率误差、区域划分、开关矢量的关系
4 电压环设计及原理
电压外环采用电压平方外环,能够提高功率和电压跟踪能力,使系统具有响应快、稳定性好、抗负载扰动能力强及结构简单的优点,文献[1,6]给出了设计参数,见式(8)。
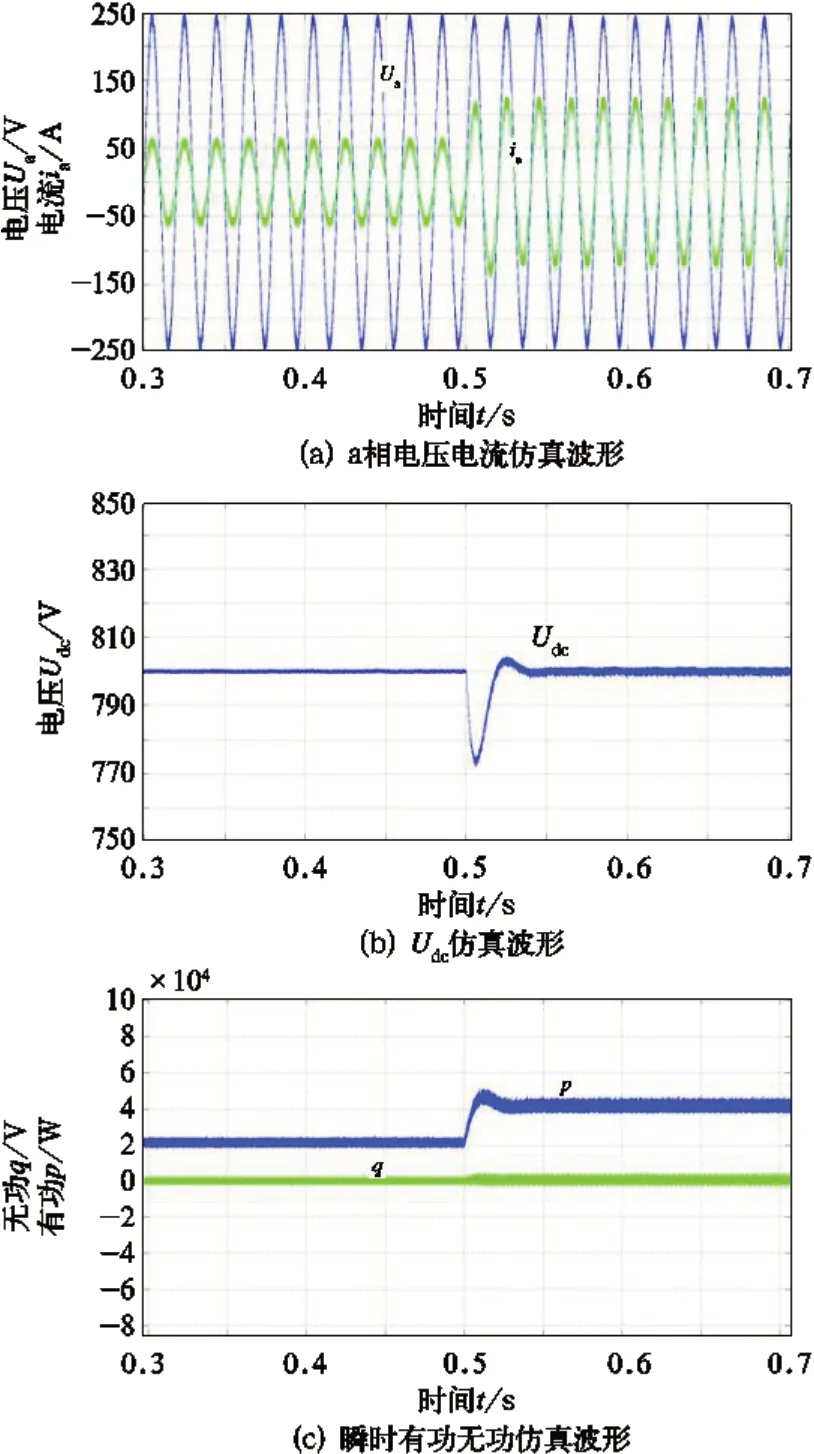
图4 基于ORS 控制a 相电压、电流、瞬时有功、瞬时无功、中间直流电压仿真波形
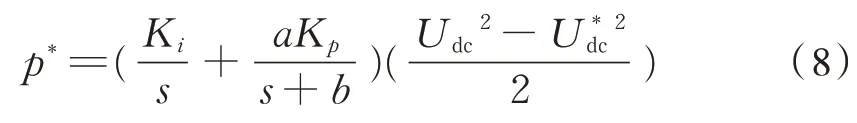
5 动态仿真验证及分析
仿真参数:线电压 300 V,f=50 Hz,L=2 mH,C=3 mF,Udc*=800 V,RL=30Ω,qref=0,Kp=a=10,Ki=150,b=500,t=0.5 s 时负载突变。
由图4(a)−4(c)可以看出采用新模型下的控制策略,系统在正常情况下,ua、ia同相位且正弦性较好;直流输出电压、有功功率、无功功率稳定在给定值附近,系统接近于单位功率因数运行。t=0.5 s 时负载突变,从图4(a)−4(c)中可以看出,系统经过在0.03 s 左右达到稳定值,表明系统具有较快的响应速度,抗负载干扰性能较好。
6 试验验证
试验模型主要参数:电网线电压380 V,交流侧滤波电感5 mH,直流电压为600 V,直流侧支撑电容3 mF,其他控制参数同仿真设置。图5(a)为基于输出调节子空间线电压电流试验波形,图5(b)为稳态运行时瞬时有功功率和无功功率试验波形。
从图5(a)可以看出,基于输出调节子空间的控制方案电压电流波形较好,且电压电流同相位,实现单位功率因素,图5(b)可以看出,稳态运行时,中间直流电压、瞬时有功功率和无功功率波形平稳,达到控制要求。

图5 基于ORS 控制的线电压、线电流、中间直流电压、瞬时有功、瞬时无功试验波形
7 结 论
通过研究分析了基于输出调节子空间的直接功率控制策略理论,通过电压平方外环和新模型下的功率内环,提高了电压和功率的跟踪能力,仿真和实验结果表明,基于输出调节子空间的DPC 系统对无功和有功都有良好的控制能力,系统的性能得到了改善,同时也验证了此控制策略的正确性与可行性。

