基于KNN 算法的高速列车车内压力模糊控制研究*

陈朝文 ，陈春俊 ，王东威

（1 西南交通大学机械工程学院，成都610031；2 轨道交通运维技术与装备四川省重点实验室，成都610031）

列车在高速通过隧道时，在膨胀波和压缩波的作用下，隧道内的空气压力发生剧烈变化，形成复杂的隧道波[1]。由于高速列车车体并不是一个完全密封的物体，车外剧烈的空气压力波动通过车窗间隙、换气系统以及车体连接处的间隙等传入车内，导致车内压力发生变化，瞬时较大的空气压力波动会引起耳鸣、头痛的症状，对乘客乘坐舒适度带来极大的影响[2−3]。目前，国内外对车内压力进行控制的方式主要有被动控制和主动控制两种，被动控制采用关闭进气阀门和废排阀门的方式，对于隧道过长和过多的路况，其控制方式无法保证车内空气的新鲜；而主动压力控制方式采用高静压风机克服高速列车运行过程中从车外进新风和排废气时遇到的阻力，保证车厢内具有相对稳定的进风量与排风量，实现抑制车外压力波动向车内传递的功能，但其运行频率唯一确定，仅能保证车内压力在合适的范围内，且能耗较大。因此，对车内压力波动控制方法的研究显得尤为重要。

根据高速列车换气系统的工作方式，对换气系统风机进行变频控制，已成为国内外对车内压力控制研究的主要方向。但大部分研究仅仅针对换气系统风机频率的控制方式，提出了基于变频风机的不同控制算法，然而对列车通过不同隧道时换气风机频率的历史控制信息的利用并不广泛。

设计一种在主动控制方式基础上，根据列车通过不同隧道时的历史控制信息，建立控制初值的计算方法，并根据列车实际运行情况，建立模糊控制系统实时改变换气风机运行频率的控制方式，实现对车内压力的有效调节，达到抑制车内压力波动的效果。

1 车内外气压传递数学模型

1.1 数学模型建立

高速列车车内压力波动主要受车体气密性缝隙造成的空气泄漏量、新风机吸入的新风量以及废排风机排出的废气量的影响[4−6]。其中，对于车体气密性缝隙造成的空气泄漏量，车体等效缝隙泄漏面积为:A=14.137 2 cm2。将车内空气视为理想气体，根据理想气体状态方程和伯努利方程得到当前时刻车体泄漏空气质量方程如式（1）:

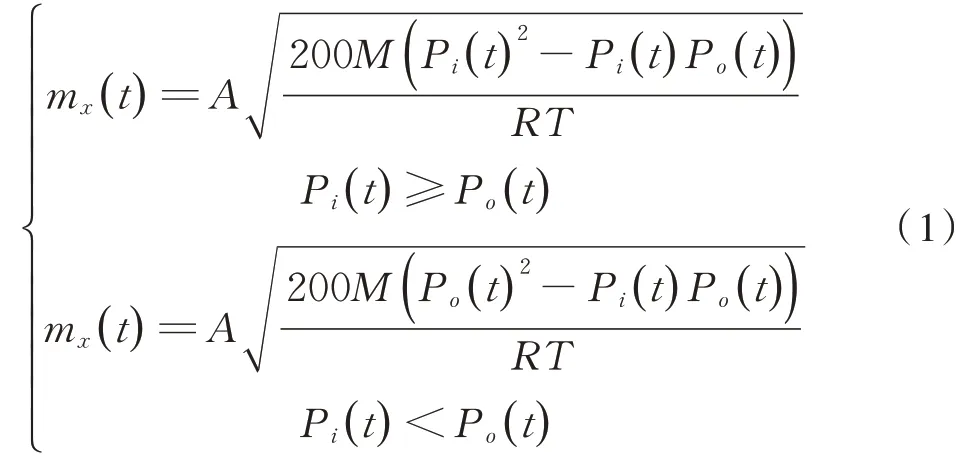
式中:mx(t)为当前时刻泄漏的空气质量流量，g⋅s−1；M为 气 体 摩 尔 质 量 ，g⋅mol−1；R为 摩 尔 气 体 常 数 ，J⋅(mol⋅K)−1；T为车内空气温度，K；Pi(t)为当前时刻车内压力，Pa；Po(t)为当前时刻车外压力，Pa。

由风机频率特性曲线、阀门流量方程等计算得到新风机质量流量与车内外压力的关系为式(2)[4]:

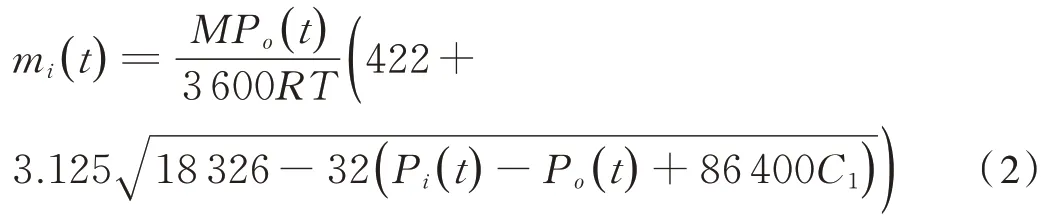
式中:mi(t)为当前时刻新风机的质量流量，g⋅s−1；C1=为新风机调速比，f0为风机额定初始频率（60 Hz），f1为新风机当前时刻的工作频率。

同理，得到废排风机质量流量与车内外压力的关系为式（3）:

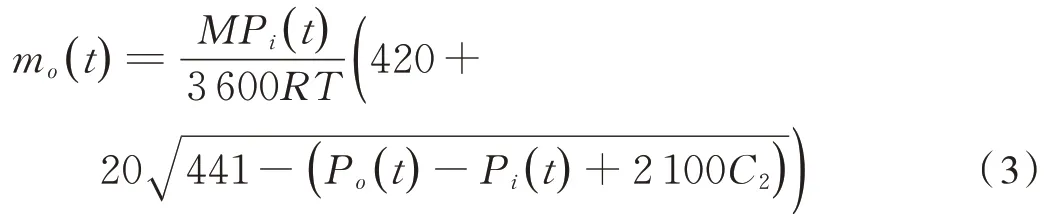
式中:mo(t)为当前 时刻废排 风机的质 量流量，g⋅s−1；为废排风机调速比，f0为风机额定初始频率（60 Hz），f2为新风机当前时刻的工作频率。

整个车内空气质量流量置换方式遵守质量守恒方程，即任意时刻新风机吸入的空气质量与废排风机排出的空气质量、车体气密性缝隙泄漏的空气质量相同。由于对高速列车经过隧道的情况进行线路实测时，实际采样频率为1 000 Hz，故车内空气质量流量变化方程为式（4）:

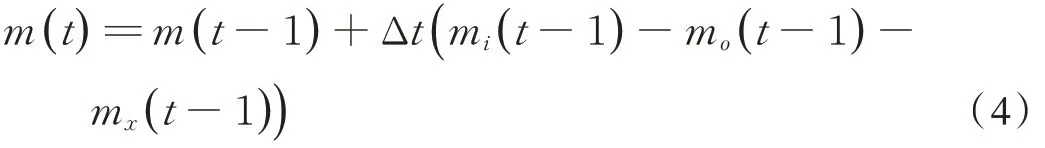
式中:Δt为采样间隔，s。

结合理想气体状态方程可得，得到当前时刻车内的空气压力变化方程为式（5）:

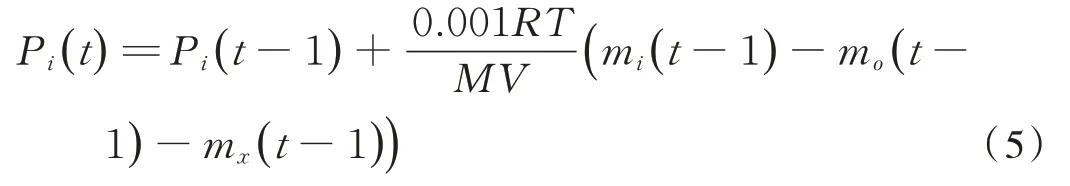
1.2 模型验证

已知一般情况下，车内压力的初始值会比车外压力高出30 Pa，高速列车车厢体积为140 m3，车内室温为20 ℃，利用simulink 建立车内外气压传递模型，以某动车实测头车会车车内外压力为例，将实测车外压力代入模型进行仿真，得到仿真出的车内压力波，实测车内外压力波和模拟出的车内压力波如图1 所示。

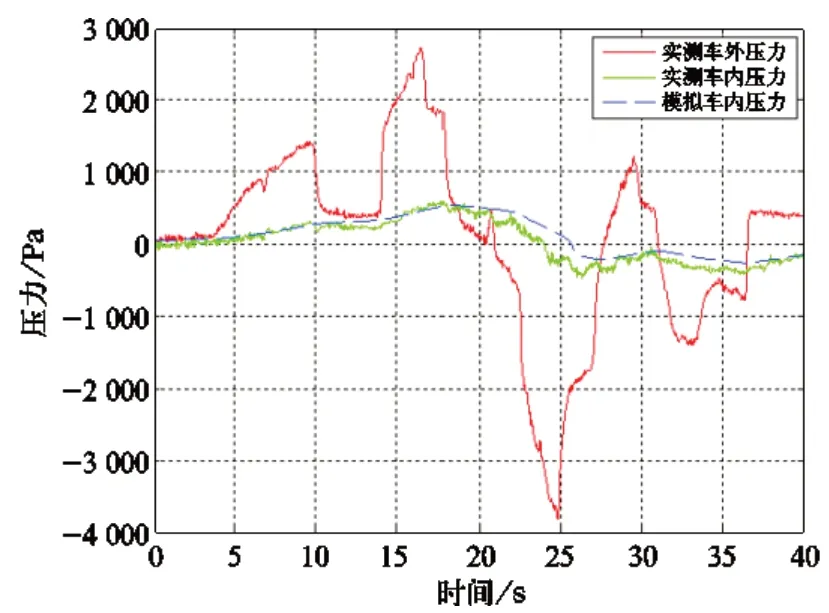
图1 模拟车内压力曲线

由图1 可得，仿真计算得到的车内压力与实测车内压力基本吻合，证明建立的车内外气压传递模型是正确的。

2 控制算法设计

2.1 总体方案设计

根据实测车内外压力信号和历史控制信息，建立数据空间DB（Database），在高速列车通过隧道的情况下，对换气风机频率进行控制仿真时，利用KNN 算法，将实测车内外压力信号与数据空间DB 中的数据进行对比，计算得到换气风机频率的初始控制信号，并带入车内外气压传递模型中。同时，利用模糊控制算法，对带入初始控制信号的换气风机频率进行控制。控制总体方案设计如图2 所示。

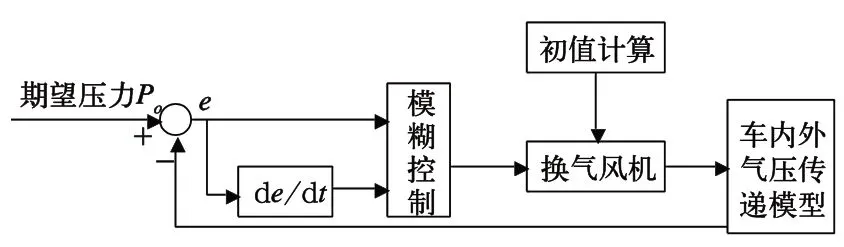
图2 控制总体方案设计

2.2 KNN（K Nearest Neighbor）算法

KNN 算法是数据挖掘技术中常用的一种分类方法，其核心思想是如果一个样本在特征空间中k个最相邻的样本中的大多数属于某一类别，则该样本也属于这个类别。借用其核心思想，KNN 算法也可以用于控制初值的提取问题中[7−9]。

假设空间DB 中有一系列点，这些点均由坐标和参数两部分组成。此时有一待查询点a，已知其坐标为q，其参数y为未知量[10]。空间DB 及查询点a结构如图3所示。

利用k最小领域搜索方法能够返回空间DB 中距离点a最近的k个点p；见式（6）:

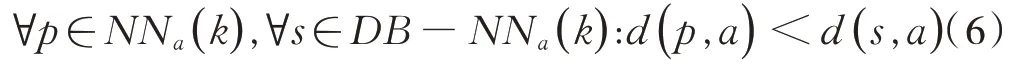
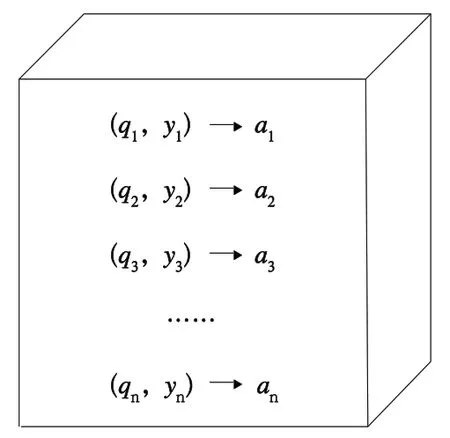
图3 空间DB 及查询点a 结构

式中:p为空间DB 中距离点a最近的点；NNa(k)为空间DB 中距离点a最近的k个点组成的点集；s为空间DB中除距离点a最近的k个点外剩余的点；DB 为空间中的一个点集；d(p，a)为点p和点a之间的距离；d(s，a)为点s和点a之间的距离。

对于一个确定的待查询点a，与k最小领域点之间的距离可以用欧几里得距离来衡量，其中h为待查询点a与k最小领域点之间的最大距离为式（7）:

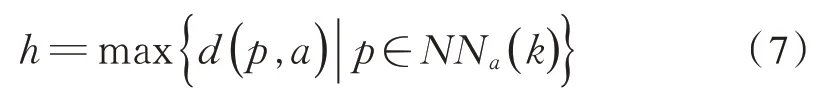
在对待查询点a的未知参数y进行拟合前，需要对k最小领域搜索方法返回的k个数据点进行赋值。k最小领域搜索方法返回的k个数据点根据与待查询点a的距离被赋予权值，距离待查询点a越近，权值越大。高斯函数具有离中心点越近，其值越大的特性，且满足随离中心点距离越远，其值均匀下降的特性。因此，运用高斯函数进行权值的计算为式（8）:

式中:d为两点之间的欧式距离；G为每个领域点相对待查询点a的权值。

根据k最小领域搜索方法返回的k个数据点以及其对应的权值，可以拟合出待查询点a的未知参数y见式（9）:

待查询点a未知参数y的计算流程图如图4 所示。

在文中，以高速列车以不同速度通过不同隧道时实测的18 组车内外压力波为坐标，以该18 组隧道压力波通过模糊控制产生的控制量为参数，联合建立数据空间DB，用于仿真数据的初值的计算。计算换气风机控制初值时，以未用于建立数据空间DB 的一组实测车内外压力波数据构建待查询点集{a}，通过KNN 算法对待查询点集{a}中的每一个数据点进行处理，计算得到每一个数据点的未知参数y，最终得到未知参数集{y}。

2.3 模糊控制算法

对于非线性系统，模糊控制比较传统的控制方法能更好的达到精确性和实时性的要求。由于建立的车内外气压传递模型为非线性数学模型，因此选用模糊控制算法对换气风机的频率进行控制。

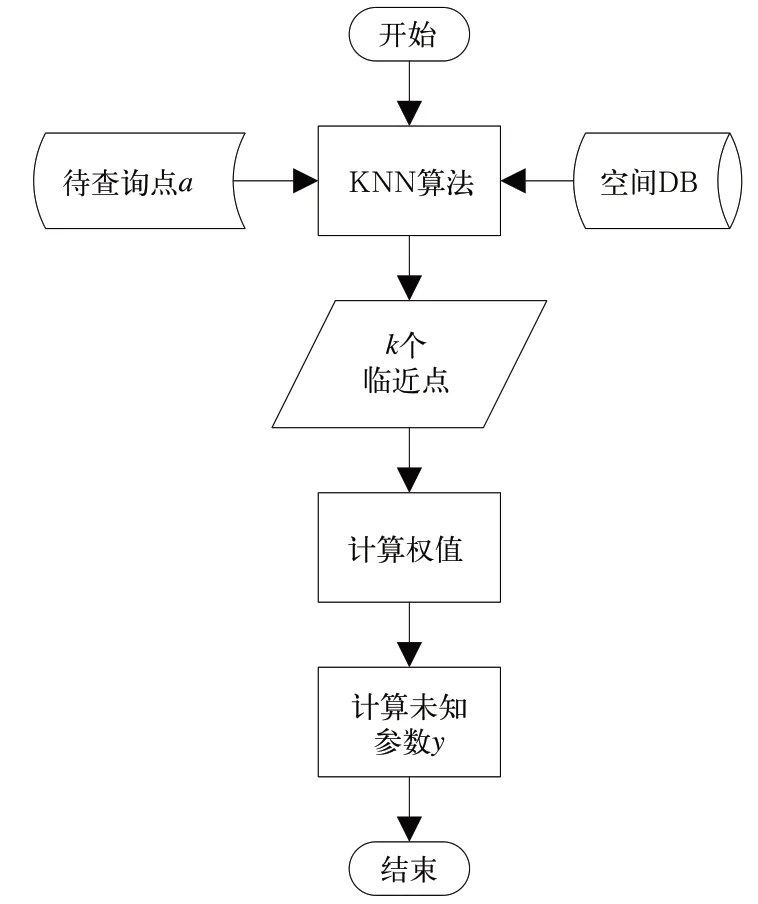
图4 待查询点a 未知参数y 的计算流程图

模糊控制的基本原理是:将实际输出信号与理想信号的偏差信号e以及偏差信号的变化率v作为输入变量，通过模糊化将输入变量转化为模糊量，再由模糊子集、模糊控制规则根据模糊推理进行模糊决策，并得到输出信号的模糊控制量，经反模糊化得到精确控制量u，并发送给执行机构，通过执行机构动作实现被控对象的模糊控制[11−15]。

文中的主要研究是根据列车实际运行状态，针对车内外气压波动，对换气系统新风机、废排风机的运行频率进行实时调节，抑制车内压力波动。设本控制系统的车内期望压力为Po(t)，车内实际压力为P(t)，则系统的偏差及偏差的变化率为:

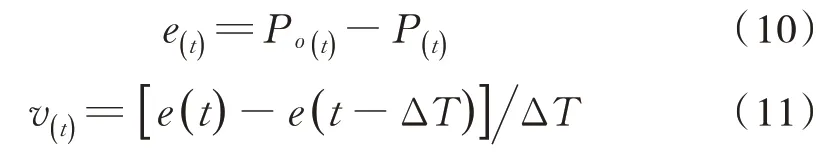
式中:e(t)为t时刻的系统偏差；ΔT为采样间隔。

系统输入输出量的模糊隶属函数采用三角函数，均用七级函数变量来定义，论域均为[−5，5]，其中车内偏差的量化因子为0.002 5，车内偏差变化率的量化因子为0.01，控制量的量化因子为0.167。建立模糊查询表如表1 所示。

文中的模糊推理算法采用Mamdani，根据模糊规则查询表，生成模糊规则查询数值表。控制量的反模糊化处理采用重心法。

由反模糊化得到的精确控制量u可得当前时刻的新风机频率及废排风机频率:

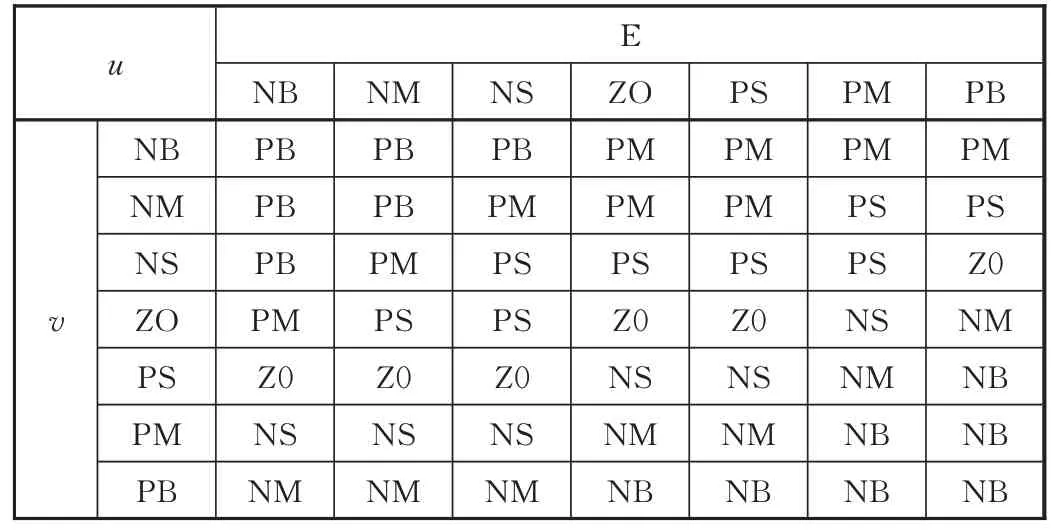
表1 模糊控制规则表

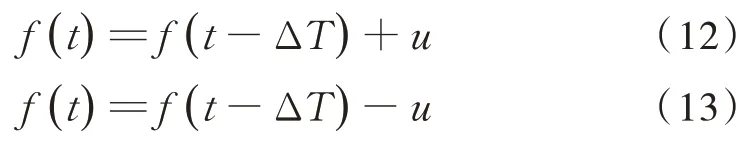
式中:f(t)为t时刻的新风机频率；f(t− ΔT)为t− ΔT时刻的新风机频率；f(t)为t时刻的废排风机频率；f(t−ΔT)为t−ΔT时刻的废排风机频率。

高速列车车内气压模糊控制模型框图如图5所示。

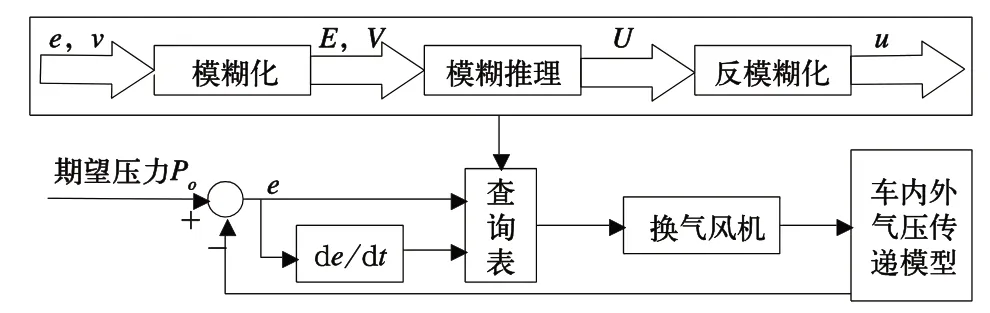
图5 车内气压模糊控制模型框图

3 仿真分析

为验证设计的基于KNN 算法的模糊变频控制算法对车内气压波动控制的有效性，选取列车在通过隧道时所得实测车内外压力进行仿真控制，并与传统的模糊变频控制进行对比，分析两种控制方式的性能。

假设高速列车上换气系统的新风机与废排风机分别由两台变频器进行控制，设定两台风机的最大工作频率均为fmax=70 Hz，最小工作频率均为fmin=0.5 Hz。

文中模拟了高速列车以297 km/h 通过隧道时的车内压力波动工况，利用仿真工具，进行基于KNN 算法的模糊控制。仿真时设置车内压力期望值为Po为零，以高速列车不同速度通过不同隧道时实测的18 组车内外压力波为坐标，以该18 组隧道压力波通过模糊控制产生的控制量为参数，联合建立数据库DB，用于仿真数据的初值的计算。计算得到两台风机的初始控制频率如图6 所示。

仿真得到两种控制方式下的车内压力波动情况如图7 所示。

同时，得到控制前、后的新风机和废排风机的运行频率如图8 和图9 所示。

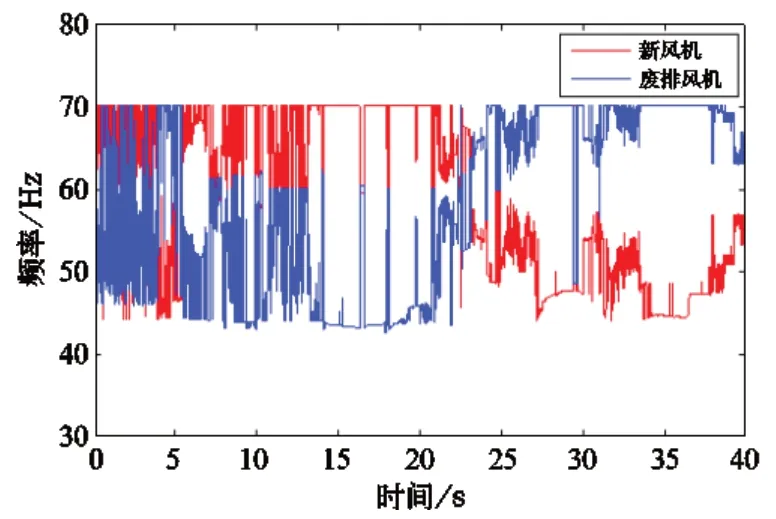
图6 风机初始控制频率

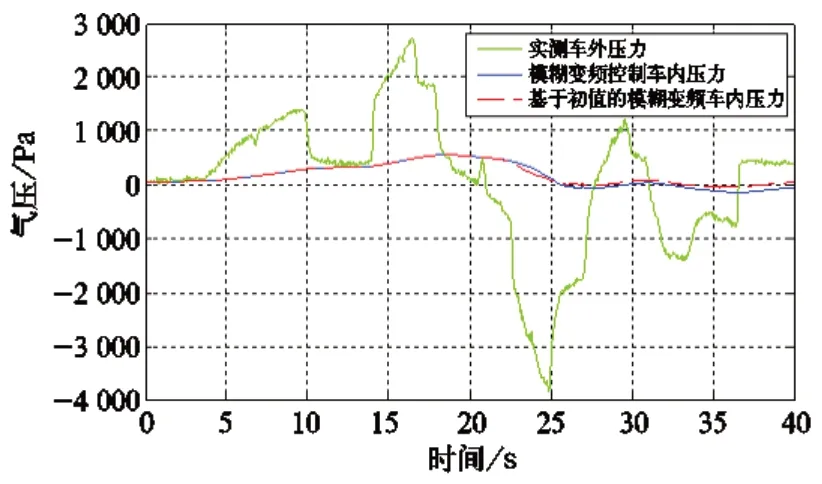
图7 车内压力控制

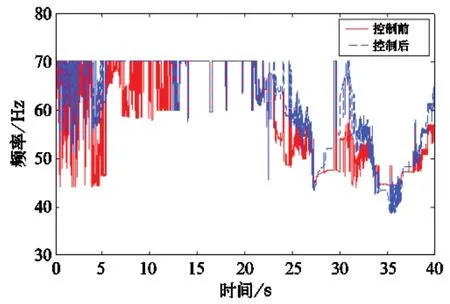
图8 控制前、后的新风机频率对比

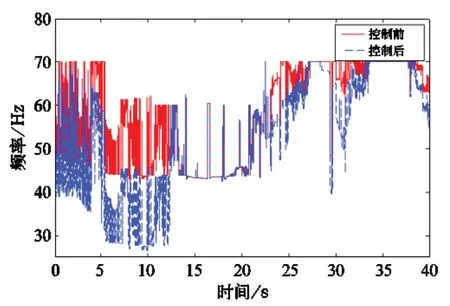
图9 控制前、后的废排风机频率对比

由图可知，基于KNN 算法的模糊变频控制后的车内压力较模糊变频控制后的车内压力更加逼近期望压力。为了对两种控制方式下的车内压力性能参数进行对比，对波动幅度、1 s 变化率、3 s 变化率进行计算并绘制图表显示。两种控制方式的1 s 变化率、3 s 变化率如图 10 和图 11 所示。

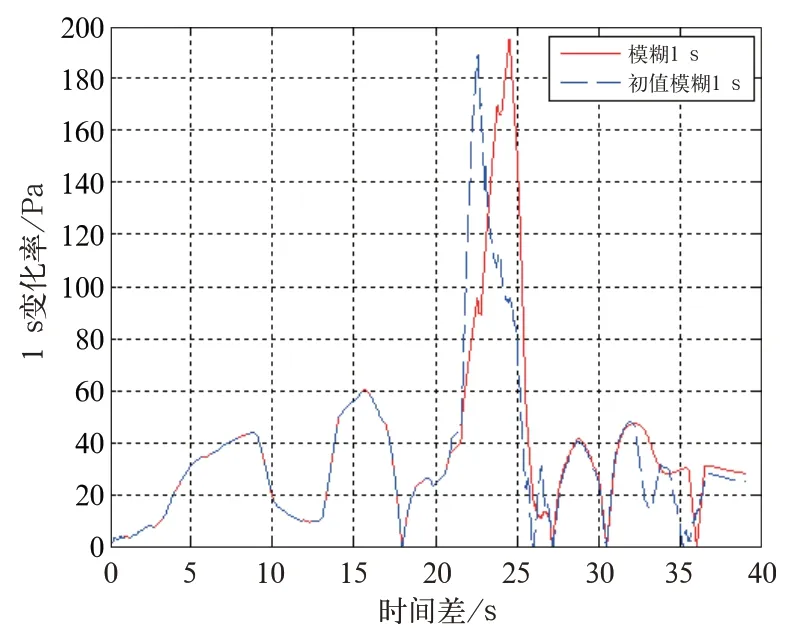
图10 两种控制方式下的车内气压1 s 变化率

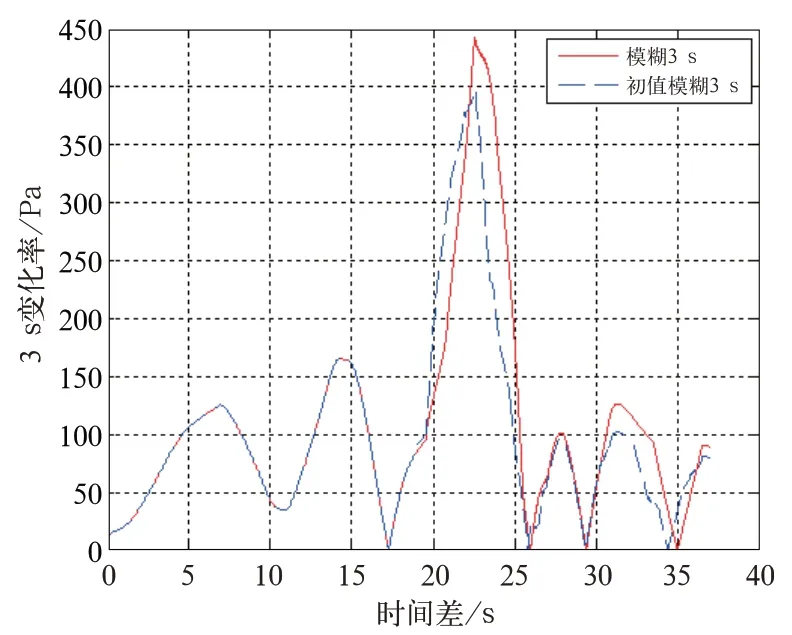
图11 两种控制方式下的车内气压3 s 变化率

两种控制算法的各性能参数对比如表2 所示。

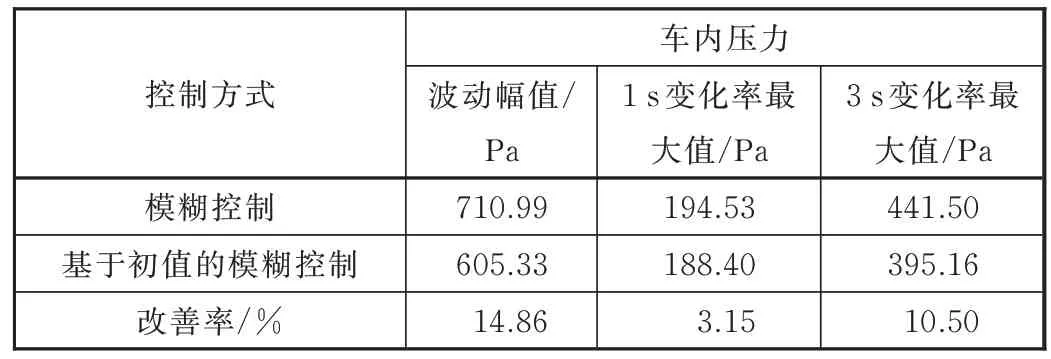
表2 车内压力性能参数表

由表2 可知，改变控制方式后，高速列车的换气系统能够更好的抑制车内压力的波动。换气系统的控制方式由模糊控制改为基于初值的模糊控制后，车内压力波动幅值由 710.99 Pa 降低为 605.33 Pa，改善了14.86%，车内压力1 s 变化率最大值由194.53 Pa 降低到188.40 Pa，改善了3.15%，车内压力3 s 变化率最大值由441.50 Pa 降低到395.16 Pa，改善了10.5%。由此可知，在基于KNN 算法的模糊控制下，换气风机起到了更好抑制车内压力波动的作用。

4 结 论

（1）通过对高速列车经过隧道时的车内外气压传递方式进行分析，建立车内外气压传递数学模型，通过仿真发现，文中建立的数学模型与实际车外压力切合度很好。

（2）基于KNN 算法的思想，建立基于历史控制信号及实测车内外压力的初值计算方式，通过该初值计算方式，能够准确的计算出控制初值；根据车内压力主动控制方式，建立车内压力模糊控制系统，该模糊控制系统能够准确算出风机频率，且能够实现对风机频率的精确控制。

（3）文中提出的控制方法相比传统模糊控制方法对车内压力波动起到了更好的抑制作用，车内压力波动性能参数均得到了较大提升，其中车内压力波动幅值降低了14.86%，车内压力1 s 变化率最大值降低了3.15%，车内压力3 s 变化率最大值降低了10.5%。

（4）由于文中所提出的算法是建立在过去的控制经验上，故可应用于类似重复作业的工程应用中，例如数控机床加工和工业机器人作业工程等。同时，由于需要利用过去的控制经验，故在过去控制经验的数量和准确性方面有一定的需求。