双连续n次积分C-半群的Laplace逆变换

李奇峰，刘 瑞，杜雨亭

(延安大学数学与计算机科学学院，陕西延安716000)

Kuhnemund在Banach空间上附加了一个比范数拓扑粗的局部凸拓扑，使得半群在局部凸拓扑下连续，从而在文献[1]中提出双连续半群的概念，使得半群理论的发展进一步深入。在上述研究的基础上，一方面王文娟等在文献[2-4]中提出了双连续C-半群以及双连续n次积分C-半群的概念，并得到了一系列结果；另一方面，施德明等在文献[5-8]中研究了几类半群的Laplace逆变换。所以本文将两者结合起来，研究了双连续n次积分C-半群的Laplace逆变换，进一步推广算子半群理论，扩展其应用领域，从而使算子半群理论更加完善。

1 预备知识

设X为Banach空间，X′为X的共轭空间。τ是X上由半范数族pτ所确定的并具有以下性质的一个局部凸拓扑。

(1)空间(X，τ)在·-有界集上序列完备。即每个·-有界柯西列在(X，τ)中收敛。

(2)τ拓扑是比·-拓扑粗且是Hausdorff拓扑。

(3)空间(X，·)中的范数可以由空间(X，τ)′定义。即对每一x∈X，有

x=sup{||：φ∈(X,τ)′，φ(X,τ)≤1}。

记φ={φ∈(X,τ)′：φ(X,τ)′≤1}，L(X)表示空间(X，·)上线性有界算子全体。不失一般性，假设p(x)≤x,x∈X，p∈pτ。

定义1[4]设C∈L(X)且为单射，算子族

{T(t)：t≥0}⊆L(X)，如果

(1)T(0)=0，T(t)C=CT(t)，t≥0；

(2)对∀x∈X，s,t≥0，有

T(t)T(s)x=

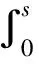
(3){T(t):t≥0}强τ-连续，即对每个x∈X，映射t→T(t)x是τ-连续；

(4){T(t)：t≥0}局部等度双连续；

(5){T(t)：t≥0}指数有界。

则称{T(t)：t≥0}为指数有界双连续n次积分C半群。

定义2[4]设{T(t):t≥0}∈G(n,M,ω,C)，对任意λ∈Λω。记

{x∈X,Cx∈Im[R(λ)]}。

线性算子A：D(A)⊆X→X定义为

Ax=[λ-R(λ)-1C]x,x∈D(A)，

则算子A称为{T(t)：t≥0}的生成元。

定义3[9]设C∈L(X)，如果函数R(·)：

D(R)→L(X)满足：

(1)R(λ)C=CR(λ)；

(2)(λ-μ)R(μ)R(λ)=R(μ)C-R(λ)C,

λ,μ∈D(R)。

则称函数R(·)为C-伪预解式。

引理1[4]A的C-预解式是如下式子：

Rc(λ,A)=R(λ,A)C=(λ-A)-1C=

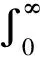
其中ρc(A)={λ:λ-A为单射且R(C)⊂R(λ-A)}。

引理2[10]F(λ)：(0，∞)→X，设F(λ)满足Laplace型表达式

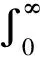
|α(t+h)-α(t)|≤Meω(t+h)，t,h≥0，

且右端积分在t的任何有限区间上是一致收敛的。

2 主要结果

定理1 设{T(t)：t≥0}∈G(n,M,ω,C)是以A为生成元的双连续n次积分C-半群，则对任意x∈X，有

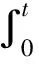
(1)

且对任意x∈D(A)有

(2)

证明由T(t)≤Meωt，故可令

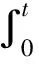
显然α(t)满足引理2的条件，有

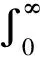
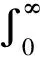
由引理2的结论有：

r>ω，

即得到(1)式成立。

用A同时作用于(1)式两端，对任意x∈D(A)有

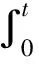
定理2设{T(t):t≥0)∈G(n,M,ω,C)是以A为生成元的双连续n次积分C-半群，则对任意x∈X，有

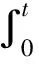
且右端积分在t的任何有限区间上是一致收敛的。

证明由定理1知道

r>ω。

对上式两边同时从0到t积分得

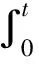
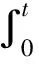
定理3 设A闭，存在ω≥0，使得s-A与r-A为单射，R(C)⊂R((s-A)n)，则

(1)若A为双连续n次积分C-半群{T(t)：t≥0}∈G(n,M,ω,C)的无穷小生成元，则

(-1)nT(t)+Hn(t)

为A生成的双连续(s-A)-nC-半群。

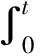
(2)若{W(t):t≥0}为双连续(s-A)-nC-半群，其无穷小生成元为A，则

T(t)=(s-A)nJnW(t)

为由A生成的双连续n次积分C-半群。

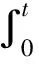
证明(1)若{T(t):t≥0}为A生成的双连续n次积分C-半群，则由文献[11]得

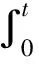
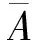
(2)由文献[10]得

再由文献[4]的定理3.2.2和定理3.2.3即得结论。

定理4 设A为X上的闭线性算子，ρ(A)≠φ,λ∈ρc(A)，A是双连续n次积分C-半群{T(t):t≥0}∈G(n,M,ω,C)的无穷小生成元，则对任意x∈

D(A)有

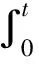
证明由定理3，A亦生成双连续(s-A)-nC-半群S(t)，由定理1的(1)得

相应于定理1的(2)有

∀x∈D(A2)。

相应于定理2有

∀x∈X。