库存对石油期货市场联动关系有影响吗？——基于随机Copula模型的分析

郭利宁 黄运成

一、问题的提出

市场联动(Co-movement)主要指资本市场上普遍存在的一种不同市场或资产价格走势趋于一致的现象(Baur，2004[1])，通常采用收益率的协同程度或价格的相关系数衡量联动关系(刘亚和张曙东，2010[2])。由于对跨市场套利、风险管控等实务操作具有较强的指导意义，一直以来都是经济学领域的研究热点(Barberis等，2005[3])。石油市场联动关系研究的发展和全球石油市场的演变及经济全球化的进程紧密相关。全球分工带来的经济一体化和期货、互换合约等石油金融产品的创新进一步增强了市场联动性(陈洪涛等，2008[4])，尤其是最重要的两个石油期货市场WTI和Brent长期以来保持较为稳定的联动关系。但是自2010年起页岩油开采技术的大规模商业应用使北美石油产量剧增，导致美国石油枢纽库欣地区(WTI期货合约交割地)库存高企。国际油价持续创新低而且WTI和Brent价差也一度接近30美元，直至2014年两市场价差才开始逐步恢复，价差异常波动的现象引起了学界的广泛关注。

WTI与Brent的价差(spread)走势和库欣库存(Cushing Shell Capacity)变化情况如图1，2010年年初WTI价格要高于Brent价格2美元左右，然后Brent价格开始高于WTI，在2011年价差达到-28美元，此后又逐步收窄到-5美元左右。如果两个市场联动关系较为紧密，那么市场间价差应该保持相对稳定，当价格走势出现较大分歧时价差则会出现波动。图1显示自2010年年初至2014年年初，随着库存的变化，两个市场的价差剧烈波动，直到2014年5月库欣库存开始大幅下降，市场价差才开始逐步恢复平稳。由图1可知在此期间市场的联动关系发生了较为明显的变化，而一般认为石油期货市场间联动性较强，各市场价格走势较为一致，不会出现价差异常变化的现象。一些石油业内人士指出库欣地区原油库存的变化会影响原油价差的走势(孔盈皓，2018[5])，虽然学界也有许多研究较为一致地认为库欣库存是导致两者价差剧烈波动的主要原因，但是仍然缺乏库存对两个市场联动关系影响的直接定量分析。

图1 库存与价差走势图

鉴于此，本文以WTI和Brent作为研究对象，首先对相关研究文献进行综述，然后引入库欣库存作为外生变量建立模型，对库存如何影响市场间联动关系进行实证分析并对结果进行解读，据此给出结论和在市场建设、风险防范方面的建议。在页岩油革命引起全球石油市场格局大变革的背景下，充分借鉴国外成熟市场的经验，研究成果可以为防范国际石油市场风险蔓延提供新思路，并为市场参与者的交易行为决策提供依据。

数据来源：美国能源信息署(EIA)。

注：库存为库欣地区库存；价差计算方式为WTI价格减去Brent价格。

二、文献综述

近些年WTI和Brent价格走势的分歧使石油市场间具有紧密联动关系的判断受到了极大挑战，许多研究将两市场间联动关系变化的原因归结为库欣库存的影响。早期关于两个市场的研究较为一致地认定WTI和Brent之间保持稳定的联动性。如Brunetti和Gilbert(2000)[6]采用ECM-FIGARCH模型捕捉到了两者的协整关系，Reboredo(2011)[7]采用多种Copula函数分析了包括WTI和Brent在内的4个石油市场间的联动关系，研究表明WTI和Brent之间的联动性最强。作为全球最重要的两大价格基准，Brent和WTI价格走势出现明显分歧的现象引发了研究人员的讨论。Scheitrum等(2018)[8]对WTI和Brent的市场价差进行了分析，研究结果显示2011年1月两者的价差关系发生了结构突变，并且库存的变化情况对结构突变具有较强的解释力。价差的变化体现出两个市场间原有的联动关系发生了改变，而Scheitrum等(2018)[8]的研究表明库存是WTI和Brent市场关系发生改变的主要原因。Pan等(2018)[9]以美国PADD2(1)PADD是Petroleum Administration for Defense District的缩写，美国石油管理局将美国划分为5个区域，其中库欣位于PADD2区，属于美国中西部地区。区域库存和PMI指数分别作为石油市场供求两端的代理变量，采用SVAR模型研究了供求因素对WTI和Brent价差的影响。她们将1994年至2016年的样本数据以2010年为分界线进行分段研究，脉冲响应分析显示PADD2区域库存对市场价差的冲击强度在2010年以后明显增强。Robe等(2016)[10]在研究中发现Brent和其他几个市场的价差变化较为正常，没有出现类似Brent和WTI之间的异常情况，进一步的实证分析则显示Brent和WTI价差的变化情况和库欣的库存情况密切相关。Tian和Lai(2019)[11]针对2011年至2015年间两市场价差先扩大后缩小的现象进行了研究，他们认为库欣地区不断上涨的库存量压低了WTI价格，导致WTI和Brent的价格走势不同。

除上述直接针对Brent和WTI价差问题的研究外，还有许多研究在一定程度上印证了库存对市场联动关系的影响。例如Bu(2014)[12]以WTI期货合约为研究对象，发现能源信息署(EIA)周库存报告对WTI市场的收益和波动均有影响。研究同时发现当市场价格处于下跌状态时，期货收益的序列相关性增强。Bu(2014)[12]的研究结果表明当库存对市场价格产生抑制作用时，期货市场价格的变化受本市场上期价格变化情况的影响增强，在这种情况下外部市场对本市场的溢出效应有所减弱，那么因为市场间溢出效应带来的联动性也会随之降低。Ye和Karali(2016)[13]分析了美国石油协会(API)和能源信息署(EIA)库存报告对石油期货市场的影响情况，他们在研究中发现库存对收益和波动均具有明显影响，并且库存报告对原油、馏分油和汽油三种代表性产品的影响效果并非一致。这种不同产品的收益和波动对库存报告反应的不对称性也有可能使得各产品的联动关系发生变化。换言之，库存对各市场影响的不一致性可能导致不同市场的走势发生分歧从而影响市场联动关系。通过分析Bu(2014)[12]、Ye和Karali(2016)[13]等的研究可以发现库存影响联动关系的两种机理：一是库存对当地市场价格走势的影响可能会降低外部市场对本市场的溢出效应从而对联动关系产生影响。二是库存对各市场的影响效果不同可能会引起价格走势发生分歧，从而导致市场间联动关系发生改变。通过对相关文献进行梳理可以发现库存影响石油市场联动关系存在一定的理论基础，但是仍然有待通过实证分析进行直接验证。

已有的研究多是针对库存如何影响价差或价格走势进行分析，如果要量化库存对联动关系的影响效果，需要通过模型建立库存和市场联动的直接关系，研究的难点在于如何将库存作为一个外生变量引入模型中对联动关系进行实证分析。以往学者大都直接分析市场间联动关系，而本研究需要在对市场联动关系进行描述的同时分析外生变量对联动关系的影响。由于具有可以对市场间非线性联动关系及尾部相依性进行分析的优势，近些年Copula模型逐步成为该领域的重要研究手段。目前国内采用Copula模型分析外生变量影响市场联动关系的研究成果有两个，一个是叶五一等(2018)[14]基于Hurn等(2016)[15]的研究提出的平滑转移Copula模型(ST-VCopula模型)，另一个则是龚玉婷(2015)[16]基于Hafner和Manner(2012)[17]的研究采用的随机copula模型。叶五一等(2018)[14]通过设置一个平滑转换条件相关系数模型(STCC)将市场波动率VIX指数作为一个外生变量引入Copula模型参数的时变过程中。他们的研究发现VIX指数是影响国家间股票市场联动性的因素之一，并且提出作为市场风向标，VIX所蕴含的信息有助于预测危机发生传染和蔓延的可能性。随机Copula模型最早由Hafner和Manner(2012)[17]提出，他们将Copula模型参数的时变演化设置为一个随机过程，并且针对似然函数中的高维积分问题提出可以使用有效重要性抽样最大似然法(EIS-ML)进行参数估计。龚玉婷(2015)[16]采用随机Copula模型对中国股票市场上不同类型指数之间的联动关系进行了分析。通过在随机过程中加入换手率作为解释变量，研究发现换手率对指数间联动关系具有明显影响。并由此提出换手率可以作为一种较为有效的信息去预测未来目标指数的相依性，从而进一步降低组合风险。ST-VCopula和随机Copula都是建立在对参数变化过程进行描述的基础上，但是引入外生变量的参数演化方程在形式上有所区别，随机Copula模型的演化方程更为灵活。

通过回顾近些年的相关研究成果可以发现库欣地区的石油库存是影响WTI和Brent市场关系的重要因素，受计量方法的限制这些研究都没有实现库存对石油市场联动关系影响程度的直接量化，而借助含外生变量的随机Copula模型可以较好地完成该研究任务。由于对含外生变量的随机Copula模型进行参数估计难度较大，所以需要使用有效重要性抽样最大似然估计法(EIS-ML)进行参数估计。EIS算法在解决高维积分问题上具有一定优势，而且可以较为方便地推广至其他类似研究。包括利率、流动性等多种因素都会对市场联动关系产生实际影响，本文为如何分析外部冲击对市场联动关系的影响提供了可借鉴的经验。

三、实证模型

(一)随机Copula模型

Hafner和Manner(2012)[17]采用一个平稳高斯自回归过程描述Copula函数的演变过程。以二元函数为例，对于两个时间序列ut和vt，在t=1，…，T时刻两者的联合分布情况由一个时变的Copula函数描述。其中θ是一个随时间t变化的Copula函数参数：

(ut,vt)～C(u,v|θt)

(1)

θt随时间的演变情况由一个不可观测的随机过程λt来决定，可以表示为Ψ(λt)=θt。与Patton(2006)[18]时变模型中Λ函数类似，Ψ是一个设置好的转换以保证参数位于Copula函数的定义域内。λt是一个潜在随机过程，服从一阶高斯自回归：

λt=α+βλt-1+υεt

(2)

其中为保证平稳性要求β的绝对值小于1，新息项ν大于0且εt～i.i.d.N(0,1)。随机过程的三个参数表示为：

ω=(α,β,υ)

(3)

通过最大似然法计算上面三个参数的估计值，得到λt随时间的演化过程，从而确定Copula函数的参数值θt随时间的演化过程，最终完成对ut和vt时变相依特征的描述。通过上述三式可以发现随机Copula其实是一种非线性滤波算法。

(二)基于有效重要性抽样的参数估计方法

对于随机Copula我们需要采用有效重要性抽样(efficient importance sampling)进行参数估计。Hafner和Manner(2012)[17]指出Copula函数是非线性的，如果采用基于正态分布的自然抽样方法(natural sampling)需要模拟的次数非常大，运算效率很低。因此，他们建议引入辅助参数(parsimonious parameters)，用有效重要性抽样方法来估计随机Copula模型。首先定义：

(4)

似然函数的通常形式是：

(5)

由于这是一个由时间T决定的T维积分，所以改成：

(6)

由贝叶斯定理可知共同出现的概率就是它们各自出现的概率的乘积，可以将式(6)改写为Copula函数的条件概率密度函数c和抽样λ的条件概率密度函数p的乘积形式。则上式改写为：

p(λt|Λt-1,ω)dΛ

(7)

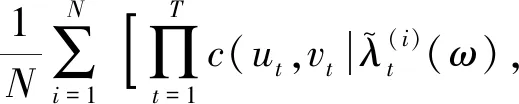
(8)

但是由于Copula是一个非线性函数，而且上式的T维积分需要模拟Λ所有可能的路径，因此这种做法不仅运算量大，运算效率也很低。事实上这种做法几乎不可能得到参数的估计值，需要对抽样方法进行修改。Liesenfeld和Richard(2003)[19]、Richard和Zhang(2006)[20]认为自然抽样器p中不含有U和V的信息是导致该问题的原因，所以考虑充分利用有效信息构造一个优化的抽样器m(λt|Λt,at)进行抽样。其中at称为辅助参数，用于对自然抽样器进行修改。从而通过模拟抽样来近似高维积分的取值。通过重要性抽样器进行似然估计的函数形式为：

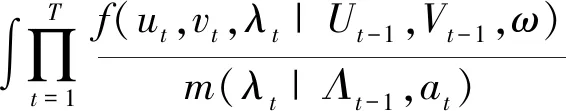
(9)

L(ω;U,V)

(10)

重要性抽样器需要尽量降低似然函数的抽样方差，其构造的难点在于如何得到辅助参数at，从而使得重要性抽样器的抽样尽可能贴近随机过程参数的真实分布情况。重要性抽样器设置为：

(11)

其中上式中分母χ是k分子对λ的积分：

(12)

进一步将k分解：

k(Λt,at)=p(λ|λt-1,ω)ζ(λt,at)

(13)

其中：

(14)

由于自然抽样器p和ζ都是高斯核，所以可知k也是高斯核。通过ζ和p的乘积形式完成ζ对自然抽样器p的修改，通过两者的乘积结果k函数和其积分χ构造重要性抽样器m，从而获得更为有效的抽样。其中重要性抽样器m在t时刻的均值和方差为：

(15)

分母χ最终的表达式为：

(16)

设置的两个辅助参数a1,t和a2,t可以对λ抽样的均值和方差进行修改。两个参数a1,t和a2,t随时间变换，所以λ的抽样就变成了一个均值和方差均随时间变化的抽样方式。用k和χ对似然函数的分子和分母进行变换：

(17)

其中χt+1(Λt;αt+1)≡1，有效重要性抽样器的辅助参数a1,t和a2,t可以通过求解下式得到：

(18)

不难得出上式等价于：

(19)

其中c和η分别为常数项和误差项，可以采用递归最小二乘法估计a1,t和a2,t。似然函数的最终形式变为：

(20)

最终EIS算法按照如下步骤执行：

(1)从自然抽样器p中抽取N个初始样本。

(2)采用递归最小二乘估计EIS的辅助参数a1,t和a2,t。

(3)依据辅助参数确定重要性抽样器m，从m中抽取N个样本。

(4)重复(2)和(3)直到a1,t和a2,t收敛。

(5)从重要性抽样器m中抽取样本，依据上式进行最大似然估计得到ω的参数值。

四、实证分析

(一)数据来源与变量描述性统计

采用库欣地区石油库存量、WTI期货价格、Brent期货价格的周数据作为研究样本，时间跨度为2007/5/11—2016/5/20，数据均来自美国能源信息署(EIA)官方网站www.eia.gov。分别计算两个市场的价格收益率，发现时间序列均具有尖峰厚尾的特点，JB检验显著拒绝了正态分布的假设。进一步的单位根检验表明时间序列均平稳，Ljung-Box滞后十阶检验结果显示序列可能存在自相关(见表1)。统计分析显示数据具有尖峰厚尾的特点，采用GARCH模型来确定变量的边缘分布情况。

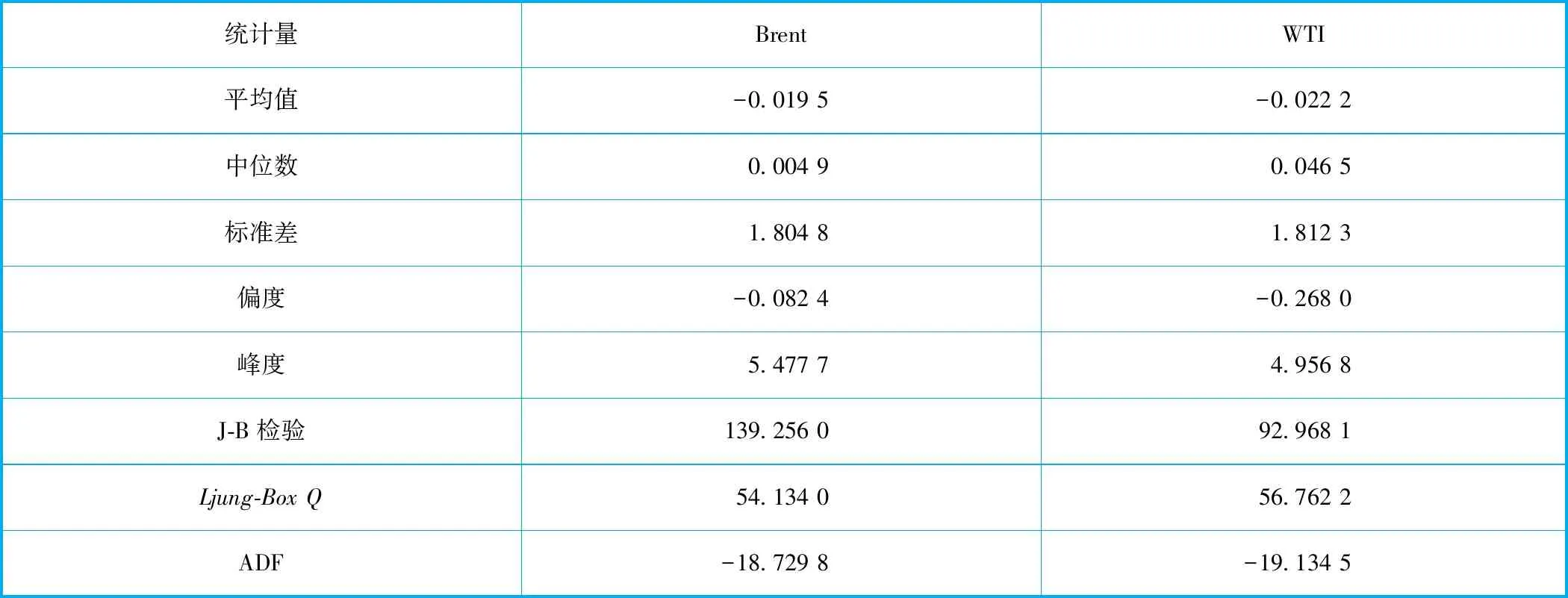
表1 收益序列统计表

(二)边缘分布拟合

Ljung-Box Q检验结果表明序列存在自相关现象，首先将均值方程设置为AR(2)自回归模型。AR自回归模型拟合检验结果表明滞后二期的变量不显著，所以选择滞后一期进行均值方程建模。对均值方程AR(1)的残差进行滞后5期的ARCH LM Test。检验结果表明自回归模型残差存在明显的ARCH效应，需要建立方差方程进行分析。

邹艳芬和陆宇海(2006)[21]发现石油价格波动序列不服从正态分布，基于t分布的GARCH模型模拟结果总是优于基于正态分布的模型。综合研究对象的偏度值、峰度值的检验结果，决定采用偏t分布的AR(1)～GARCH(1，1)-skew-t模型。其中，残差εt服从自由度为ν、偏度为的t分布。

(21)

对GARCH模型拟合后得到的标准化残差序列进行滞后5期的ARCH LM Test。结果显示WTI所有滞后期的标准化残差序列检验无法拒绝不存在ARCH效应的原假设，Brent自第2期之后所有标准化残差序列检验无法拒绝不存在ARCH效应的原假设，GARCH建模符合研究要求。

表2 收益率时间序列的ARCH LM Test

表3 残差序列的ARCH LM Test

AR(1)-GARCH模型建模结果如表4所示。ARCH项和GARCH项均显著且α+β<1，三个序列两者之和均接近1，表明波动有较强的持续性。除Brent和WTI的方差方程常数项之外所有变量均显著，ARCH项和GARCH项均通过检验且两系数之和α+β<1，表明建模满足平稳性要求。均值方程中滞后一期的系数略大于0.2，总体来看显示上期收益对本期收益的解释能力相对较小，市场价格的变化情况较为复杂。对残差序列做标准化处理，并进行概率积分变换得到累积分布序列，使用K-S检验法检验累积分布序列是否服从[0，1]上的均匀分布。表4中K-S 统计量的概率值均比较大，说明经过概率积分变换后的序列服从均匀分布。

表4 GARCH拟合边缘分布参数及检验

(三) 随机Copula建模

对库存进行指数变化率处理并在随机Copula模型中引入库存的指数变化率作为外生变量。考虑到2010年前后库存对市场联动关系的影响效果可能发生改变，将整个时间段分为2007/5/11—2009/12/25和2010/1/1—2016/5/20两部分进行考察，参数演变过程设置如下：

λt=α+βλt-1+D1δ1xt+D2δ2xt+υεt

(22)

其中xt表示库存的指数变化率，D为哑变量。在第一分段中D1=1，D2=0，第二分段中D1=0，D2=1，对应的参数δ1和δ2代表在不同时期库存对市场联动关系的影响效果。由于随机Copula模型参数的最大似然估计是一个高维积分，所以采用有效重要性抽样的极大似然(EIS-ML)方法进行参数估计。为了保证似然估值的光滑性，在EIS 算法中采用同一组普通随机数(common random numbers，CRNs)来产生样本。设定抽样数S=200，EIS迭代5次，参数估计结果见表5。

表5 随机Copula模型估计结果

表5中列出了五种Copula函数的参数估计结果，参数显著性检验和对数似然值显示建模情况符合研究要求。所有Copula函数的随机过程一阶自回归项系数β在统计上均高度显著，表明两个市场的联动关系具有一定持续性，两者当期的联动情况能为预判下期价格走势的协同程度提供一定信息。但是这种持续性会衰减，当期两市场的联动情况对几周后市场联动关系的预测能力较差。Clayton、Gumbel及其镜像函数可以对市场间尾部相关性进行描述，它们的自回归项系数β显著则表明市场间极端风险传染的状况也具有一定的持续性。换言之，当期两个市场价格共同发生陡升(陡降)的极端情况会对下一期是否也会发生价格同时陡升(陡降)产生一定影响。

除Clayton外其他四个模型的δ1均不显著，表明2010年以前库存不是影响市场联动关系的显著因素，而三个模型中δ2具有显著性表明这种情况在2010年以后发生了变化。通过对比Gumbel、Clayton及其镜像函数的δ2，可以发现2010年以后库存对市场上、下尾部相关性的影响具有一定非对称的特征：Gumbel和Rotated Clayton两个函数只能描述市场间上尾相关性而无法分析下尾相关性，这两个模型中外生变量的参数δ2在统计上不显著表明库存对市场的上尾相关性不具有明显的影响力；同理，Clayton和Rotated Gumbel模型中外生变量的参数δ2具有较强的显著性表明2010年以后库存因素对市场的下尾相关性具有显著影响。库存对市场上下尾相关性影响效果不对称的可能原因有两个：一是页岩油革命以后石油产量剧增，市场整体走势处于库存上涨不断压低石油价格的状态，而库存降低引起石油价格陡升的情况较少发生，所以实证分析只显示出库存的变化对市场下尾相关性有一定影响；二是市场价格发生大幅上涨的情况多是由于金融因素所致，库存降低对价格抬升的作用较为有限，无法引起两个市场石油价格同时大幅上涨，所以库存对市场间上尾相关性不具有显著影响。所有函数的δ2值均小于0，表明库存和市场联动性存在反向关系：库存降低则市场联动性增强，而库存升高抑制市场联动性。

实证分析结果表明库存会影响石油期货市场间联动关系，探究库存对联动关系的影响机理离不开对两个市场性质的剖析。Brent是包括期货、远期和即期现货在内的一个市场体系，其中Brent期货合约采用期转现和现金两种交割方式。在期货合约最后交易日结束后，未平仓的Brent期货合约可以通过期转现交割，由期货头寸转变为远期头寸，如果采用现金交割，那么结算价取决于交割月前21天的北海地区石油贸易价格。可见，本质上锚定Brent期货合约价格的是石油贸易因素。反观采用实物交割方式的WTI期货合约，其交割地库欣的石油现货库存对WTI期货价格走势有较强的直接影响。不仅EIA每周发布库存公报，很多参与交易的机构投资者也在自己搜寻库存信息，库存之所以被重视是因为库存情况和市场风险溢价、便利收益高度相关。Michail(2019)[22]等在研究中就发现便利收益对WTI和Brent市场价差有明显影响，背后的机理就是库存通过改变便利收益扭转了WTI期货价格走势从而导致WTI和Brent价差升高。较高的库存可以压低风险溢价和便利收益，导致WTI期货合约价格和库欣地区的库存现货价格更加接近。2010年以后库欣地区石油现货价格明显降低且库存量大幅升高，期货价格开始跟随现货价格下降。而当库存处于低位时，石油则通过贸易渠道流入库欣地区，影响WTI期货价格走势的主要因素则变为石油贸易。通过分析我们可以发现，只有当库欣库存较低时石油贸易会将两个市场连接得更为紧密，因此市场联动性增强；而库存较高时WTI期货价格走势主要取决于库欣当地的库存价格，Brent价格变化依然由全球石油贸易情况来决定，所以不难理解库存升高会导致两个市场联动性降低。Kao和Wan(2012)[23]就曾经在自己的研究中指出库欣地区库存的上升严重妨害了WTI作为全球性石油价格基准的地位，依据本文的分析，只有在库欣库存较低时WTI的价格走势才能更多地反映全球石油贸易情况，而库存处于高位时WTI和外部市场的割裂较为严重。

进一步分析两个市场联动关系的时变情况，运用粒子滤波法( particle filter)(Gordon等，1993[24])得到时变相关系数图(见图2)。图2为参数δ2显著的三个Copula函数的时变相关系数图。虽然因Copula函数设置形式不同导致三个模型的时变相关系数值不完全相等，但是相关系数随时间变化的情况基本保持一致。时变相关系数图显示总体上两个期货市场间联动关系较为紧密且具有明显的时变特征，2010年后相关系数的平均水平较2010年之前有明显的下降(排除金融危机期间)，表明WTI和Brent的联动关系在2010年以后有明显的减弱。图中显示在2008年年末到2009年年初金融危机期间相关系数均出现大幅降低，可见金融危机对期货市场的联动关系产生强烈的影响。2010年至2014年期间相关系数波动明显增强且系数值减小，在时间上对应库存处于高位的时期，印证了库存升高会降低市场联动性的判断。

图2 时变相关系数

通过相关系数的时变分析可以发现金融危机和页岩油革命对石油市场联动关系的影响具有显著的不同：金融危机期间市场联动性迅速且猛烈地减弱，但是之后也得以较快地恢复；页岩油革命期间市场联动关系的减弱则具有较强的持续性。目前普遍认为机构投资者对石油市场具有较强的影响力是导致石油市场金融化的主要因素之一，而石油市场的金融化使得市场间联动性增强。金融危机爆发前在各路资本的追逐下石油价格一度攀升至147美元，但是金融危机重创了全球金融业，加之监管措施的调整和全球经济形势的低迷导致资本撤离石油市场，市场对金融紊乱引起的变化做出了较为迅速的反应，所以联动关系的变化也较为迅速。2010年以后页岩油革命导致世界石油市场格局发生根本性的变化，与Brent作为全球石油贸易的基准不同，库欣地区库存的上升使得WTI开始更多地受到本土石油市场供求基本面的影响，两者价格走势开始出现分歧，联动关系跟随库欣库存的升降而波动。

五、结论与启示

本文以2007—2016年WTI、Brent期货合约数据和库欣地区库存数据作为样本，通过引入库存作为外生变量建立随机Copula模型，分析库存对石油市场联动关系的影响情况，并对两者联动关系的时变特征进行描述。研究发现：(1)2010年以后库存对石油期货市场间联动关系有显著影响，而在2010年以前库存对石油市场联动关系的影响不显著。(2)实证分析显示库存升高会抑制市场联动性而库存降低则市场联动性增强，且库存对市场间下尾相关性的影响具有显著性，对上尾相关性的影响不显著。(3)市场间联动关系具有一定持续性，当期市场间极端风险传染情况对下一期是否也会发生极端风险传染有一定的预测能力。(4)时变相关系数分析显示金融危机期间市场联动关系大幅减弱然后迅速恢复，页岩油革命发生后市场联动关系有明显减弱且尚未恢复到2010年之前的水平。

WTI和Brent之间的跨市场套利是全球石油市场上一种重要的交易，几乎所有的石油金融产品都围绕这两个期货合约建立头寸，两者的联动关系是制定交易策略时需要考虑的重要因素。长期以来没有给予库存因素足够的重视，导致现有的分析模式已经不适合应用于石油跨市场套利等操作。通过采用新的计量模型进行分析，本研究带给我们如下启示：(1)目前库欣地区的库存仍处于高位，由于全球经济增速减缓叠加页岩油产能增长，库存总量还会不断升高，在可预见的一段时期内WTI和Brent的协同性较弱，各市场价格走势和价差变化情况将较为复杂。建议投资者在构建和交易头寸时应充分考虑库存对市场联动关系的影响，为防范极端事件发生应增加持有头寸的多样性。(2)尤其要注意库存只对市场下尾相关性具有显著影响，投资者应根据库存实际情况及时调整交易策略。目前整体上石油价格处于下行趋势，库存升高使得市场间下尾相关性减弱，两个市场同时发生价格陡跌的概率降低。这意味着有可能出现一个市场价格猛烈下跌但另外一个市场价格保持相对稳定(甚至升高)的情况，此时价差的剧烈波动会增大交易者操作难度。

研究成果对我国原油期货合约市场的风险防范和市场建设同样具有一定的借鉴意义。研究表明增加库存能有效缓冲市场间溢出效应，积极完善交割库、扩大可交割规模能有效抵御外部冲击，有助于我国原油期货合约市场的平稳发展。

整体上石油市场呈现脱虚向实的趋势，金融因素对石油市场的影响力在下降，石油市场开始向供求基本面决定市场走势回归，与金融危机相比页岩油革命对全球石油市场的影响更为深远。应该把握当下难得的机遇期，通过改革石油市场流通体制推进石油现货市场的建设，进一步充实、完善我国石油储备体系。现货市场和石油储备作为广义的石油库存有助于防范外部风险，建设多层次且具有一定深度的市场体系有利于形成科学合理的石油定价机制，从而最终打造一个反映中国石油供求关系并对亚洲乃至世界石油价格产生重大影响的石油价格基准。