基于动态遗忘因子递推最小二乘法的永磁同步电机参数辨识算法

方桂花 王鹤川 高 旭

(内蒙古科技大学 内蒙古 包头 014010)

0 引 言

内置式永磁同步电机(IPMSM)因功率密度大、体积小、效率高等优点被广泛应用于电动车辆的动力系统[1-2]，然而在车辆行驶过程中，IPMSM的环境温度变化较大，导致电机参数存在一定程度的变化。为了确保IPMSM控制系统的高精度控制以及应对参数变化能力，提高在线识别电机参数算法的精度与抗干扰能力成为关键研究内容[3-4]。

目前应用在IPMSM控制系统的参数辨识算法主要有最小二乘法、卡尔曼滤波法、模型参考自适应法、人工智能识别法。文献[5]提出了一种高效率的递归卡尔曼滤波法，能够将系统信号与不完全噪声有效分离开，在参数识别算法的抗干扰能力上取得了有效进展，但目标函数不易确定、算法设计难度大等缺点较为明显；文献[6]设计了一种模型参考自适应算法辨识表贴式永磁同步电机参数，与卡尔曼滤波算法相同的是，算法易于实现的特点需要建立在d轴电感与q轴电感相等的条件下，当模型待辨识参数较多时，自适应律的确定变得十分困难。这两种算法在IPMSM控制系统中应用受到极大限制。文献[7]设计了一种变步长的Adaline神经网络参数识别算法，将步长与瞬时误差的二次方建立对应关系，在提高收敛速度的同时增加了系统稳态误差，并且容易存在较大的失调。

递推最小二乘法(RLS)以结构简单、识别精度高、收敛速度快等优点在IPMSM参数在线识别中得到广泛应用。文献[8]在RLS算法的基础上加入遗忘因子，降低数据储存量的同时，提高了算法的跟踪性能，同时在一定程度上降低了算法的抗干扰能力。文献[9]将带遗忘因子的最小二乘法应用到永磁同步电机参数识别中，可以同时识别惯性、负载转矩和摩擦系数，保证控制系统在复杂的环境下具有良好的动态性能。但是在目前IPMSM参数识别算法中遗忘因子λ的大小为恒定值，在λ较小时算法收敛速度得到提高，同时会降低RLS对噪声的鲁棒性，λ取值偏大会产生相反的控制效果，λ的大小设定直接影响RLS算法识别性能。

为解决上述问题，本文设计一种基于动态遗忘因子递推最小二乘法的永磁同步电机参数辨识算法。在每次迭代过程中，根据当前理论模型与实际模型的输出值之差ε(k)，建立遗忘因子动态函数，实时调整λ的取值，在保证算法较快的收敛速度以及较高的稳态抗噪声鲁棒性的同时，提高算法的综合性能。

1 IPMSM参数辨识模型

IPMSM是一种多变量、非线性、强耦合设备，为提高控制系统的控制精度，通常采用转子磁链定向的向量控制策略，经过坐标变换后，在d-q同步旋转坐标系下，永磁同步发电机定子电压方程：

(1)

式中：R为定子相电阻；Ld、Lq为直、交轴同步电感；id、iq、ud、ud为直交轴电流电压；ψf为永磁转子每极磁链；ωe为同步电角速度。

通过帕德逼近法将上述微分模型离散化[10]，并将离散结果化简为如下形式：

id(k)=βd1id(k-1)+

βd2[ωe(k)iq(k)+ωe(k-1)iq(k-1)]+

βd3[ud(k)+ud(k-1)]

(2)

iq(k)=βq1iq(k-1)+

βq2[ωe(k)id(k)+ωe(k-1)id(k-1)]+

βq3[uq(k)+uq(k-1)]+

βq4[-ωe(k)-ωe(k-1)]

(3)

式中：系数βd1-βd3、βq1-βq4与电机参数Ld、Lq、R、ψf系统采样时间T的数学关系如下：

(4)

(5)

为了降低在求解过程中的计算量，选用式(2)作为参数估计的基本模型，对参数Ld、Lq、R进行在线估计，简化式(2)可得：

y(k)=φT(k)θ(k)

(6)

式中：y(k)=id(k)；

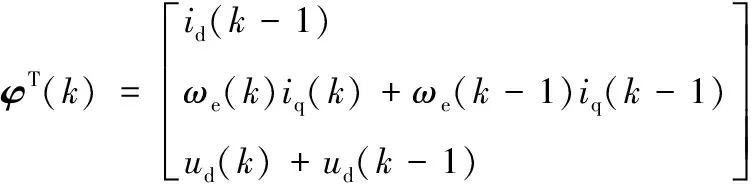
y(k)=φT(k)θ(k)+e(k)

(7)

式中：e(k)为噪声信号。

采用递推最小二乘法，通过上述模型辨识出参数矩阵θ(k)后，再通过式(4)得出IPMSM的电阻、电感参数辨识值。

2 RLS算法

2.1 传统RLS算法

递推最小二乘法在参数识别过程中，实时采集IPMSM的交、直轴电流、电压作为系统输入矩阵，通过准则函数估计值来不断修正参数矩阵，使准则函数值最小化。在加入遗忘因子后，控制器将每次迭代累积的数据“遗忘”，降低协方差矩阵的饱和度，突显新数据的作用。在上述参数辨识模型的基础上，建立RLS递推公式为：

(8)

2.2 动态遗忘因子RLS算法

在目前IPMSM应用的RLS参数辨识算法中，遗忘因子λ为固定值，对RLS算法的收敛速度以及对噪声的抵抗能力的影响是矛盾的，不管如何取值遗忘因子都会牺牲算法的一些能力。为解决上述问题，本文在传统IPMSM的RLS参数识别算法中引入动态遗忘因子，依据当前理论模型与实际模型的输出值之差ε(k)，动态调整遗忘因子的大小。由RLS递推公式可知，在k时刻ε(k)的值可表示为：

(9)

在辨识过程中，ε(k)可以表示辨识效果，主要由辨识误差和噪声引起。在ε(k)较大时，需要降低遗忘因子的取值，使算法快速收敛；在ε(k)较小时，需要对遗忘因子取较大值，以保证算法的辨识精度以及抗噪声能力。

依据上述思想，建立动态遗忘因子函数为：

λ(k)=α+(1-α)e-γε(k)

(10)

式中:α为一个接近并小于1的正可调数；γ为正可调参数。由式(10)可知，在ε(k)取值较大时，遗忘因子取值接近α；ε(k)取值较小时，遗忘因子取值接近1。

将遗忘因子改为动态函数后，可得RLS递推公式为：

(11)

3 仿真验证

为验证本文设计算法的正确性，在MATLAB/Simulink中搭建IPMSM控制系统，嵌入S-function函数搭建的固定值遗忘因子RLS参数识别算法与动态因子RLS算法，对比两者的控制效果。IPMSM系统关键参数如表1所示。

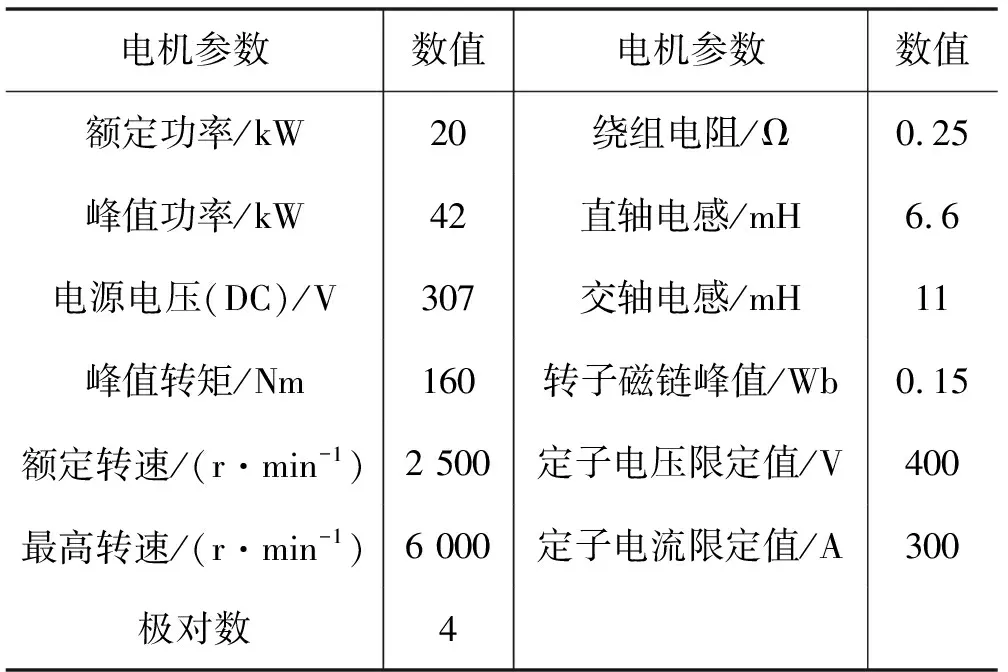
表1 永磁同步发电机参数表

仿真设置RLS算法的协方差与参数初始值为：P(0)=(106)I，θ(0)=(10-6)[1,1,1]噪声e(k)均值为0，方差为0.5的正态分布信号。设置仿真时间为0.3 s，仿真步长0.005 s，IPMSM的参数在0.15 s由11 mH突变为11.1 mH。首先设定遗忘因子λ分别为0.945、0.965、0.985、0.995，观察RLS参数识别算法结果如图1所示。

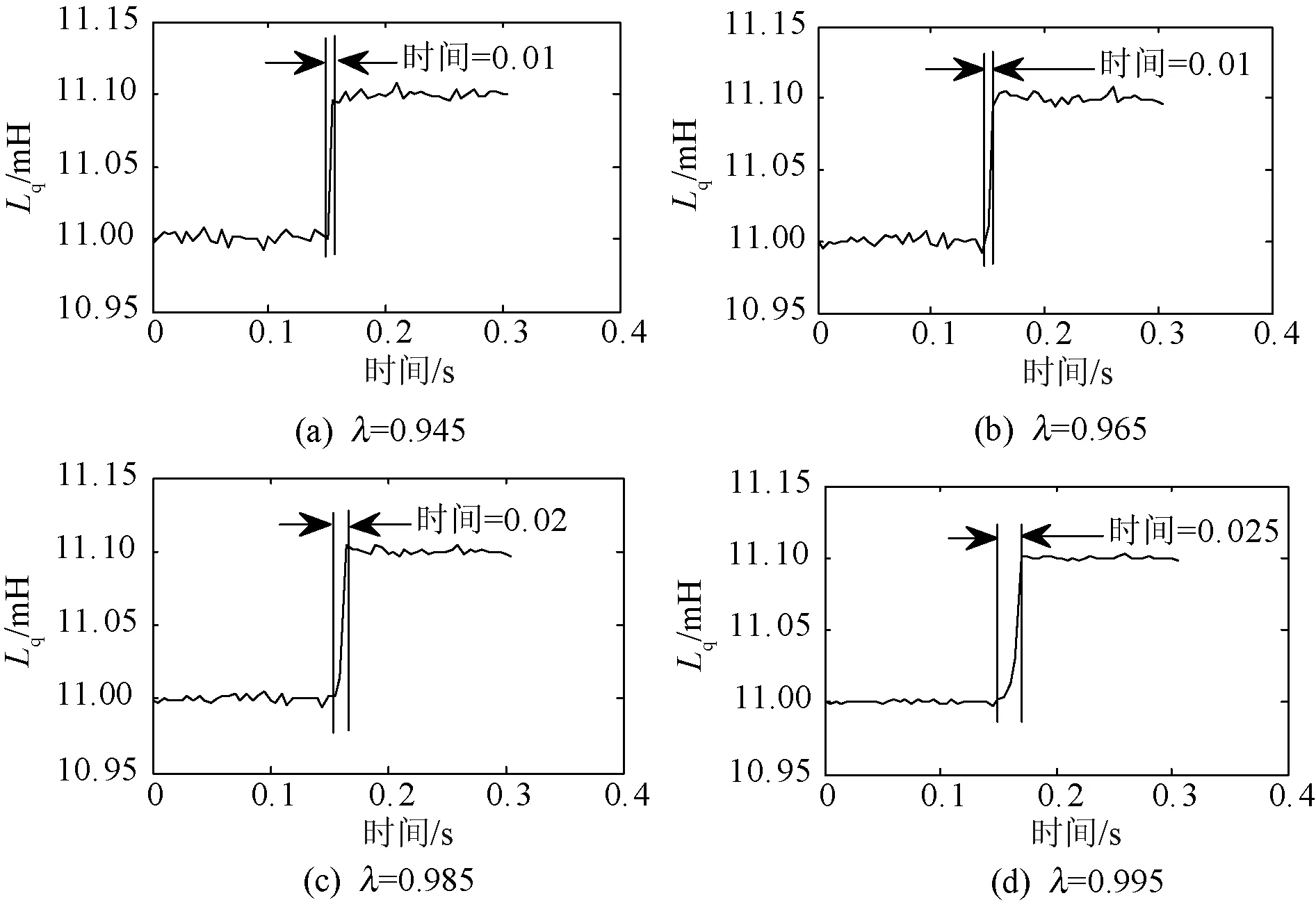
图1 参数辨识结果

由图1可知，遗忘因子较小时，RLS算法收敛速度快，但是稳态情况下易受噪声影响，相反情况下，遗忘因子取值越大，RLS算法的收敛速度变慢，但稳态效果良好，不易受噪声干扰。并且遗忘因子λ取0.945和0.965时，收敛速度视为相同，故在设计动态遗忘因子函数时，可调参数α设定为0.96。

可调参数γ直接影响了动态遗忘因子λ在参数α与1之间的变化情况，设置参数γ分别为2、4、5，在RLS算法参数识别过程中，动态遗忘因子调整过程如图2所示。

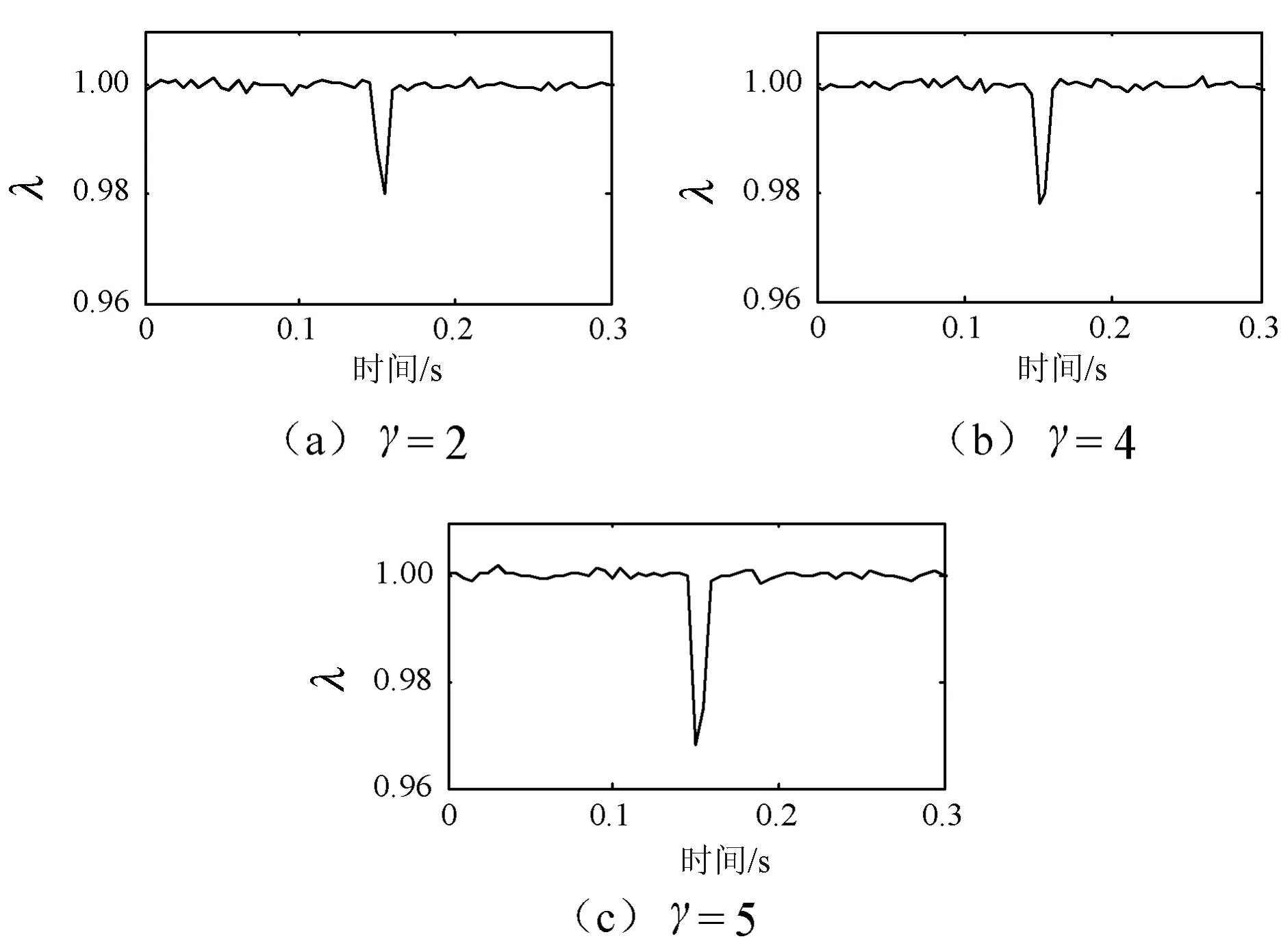
图2 动态因子调整过程

为了使遗忘因子分布在α与1之间，选择参数γ为5，至此确定动态遗忘因子函数。

在RLS算法中嵌入动态识别函数后，IPMSM的参数Ld、Lq、R，以及识别结果如图3所示。

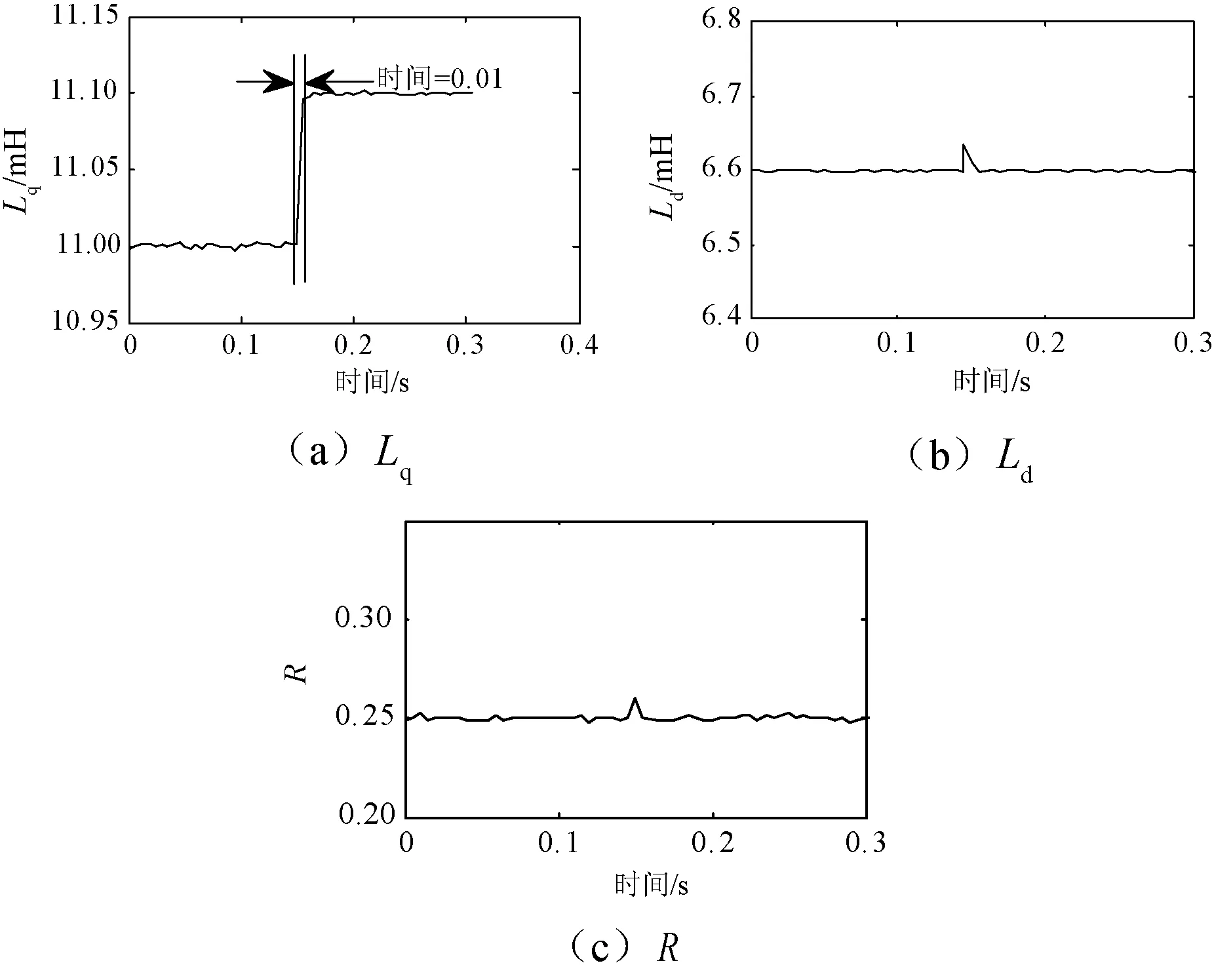
图3 改进RLS算法参数识别结果

由图3(a)与图1(a)-(d)对比可知，动态遗忘因子的RLS参数辨识算法在动态情况下可以保证较快的收敛速度，在稳态时，可以保证算法的稳态精度，相比固定值RLS算法综合性能更强。

4 结 语

本文在分析遗忘因子对最小二乘参数识别算法的收敛速度以及抗噪声干扰能力影响的基础上，提出内置式永磁同步电机的动态遗忘因子RLS算法。根据当前理论模型与实际模型的输出值之差ε(k)，建立遗忘因子动态函数，实时调整λ的取值，实现遗忘因子动态调整。仿真结果表明，改进算法在保证算法较快的收敛速度以及较高的稳态抗噪声鲁棒性的同时，提高了算法的综合性能。