基于同态高低通滤波与多尺度Retinex的低照度彩色图像增强
张江鑫 杨 惠
(浙江工业大学信息工程学院 浙江 杭州 310023)
0 引 言
在低照度条件下,图像的很多有效信息无法显现,重要的细节信息也会丢失[1],如在低照度情况下,视频监控图像的细节难以分辨,这给信息的提取带来了阻碍,进而直接影响了目标检测、识别与跟踪的性能。因此,对于低照度彩色图像增强方法的研究具有重要的意义。
低照度图像增强方法主要有:直方图均衡化及其改进算法,同态滤波算法及其改进算法,Retinex算法及其改进算法。Kim[2]提出的保持亮度的双直方图均衡化算法(BBHE)比较简单,但存在过度增强、部分细节丢失的缺点。自适应直方图均衡化增强及其改进算法[3-4]主要通过计算图像的局部直方图,提升图像对比度,但增加了噪声。传统同态滤波算法可以消除图像照明不均的问题,增强暗区的细节又不损失亮区的细节,文献[5-6]提出改进的同态滤波算法,但其参数过多,处理不方便。经同态滤波处理后的图像,整体处于偏暗的状态,并且滤波传递函数参数过多,设置繁琐。因此,文献[7-9]提出改进的同态滤波传递函数,使得设置参数减少的同时,能够达到更好的图像增强效果。文献[10]将改进的同态滤波算法与对比度受限的自适应直方图均衡化算法相结合,对图像增强有较好的处理效果。Retinex算法具有提高图像对比度,突出细节,改善图像色彩的恒常性等优点,但其易产生光晕现象,使得处理后的图像不自然。
本文针对上述存在的缺点,提出改进算法。本文算法对颜色分离后的三个分量图像进行同态高低通滤波,在提取高频成分的同时,保留部分低频成分;采用多尺度Retinex算法、指数变换和量化对高频成分进行处理,增强高频图像的细节并提高对比度;为避免低频图像部分区域过度明亮或失真,对低频图像进行量化和线性伸缩变换,从而进一步提升了视觉效果。
1 同态滤波算法
同态滤波算法主要是通过调整灰度范围和增强对比度来改善图像的质量。其原理是:通过减少照射分量,使得低频成分削弱,光照范围减少,进而降低了灰度级范围,与此同时,反射分量即高频成分增强,则图像的细节就被增强。对于一幅图像S(x,y),可以分解为两个不同的图像:对应高频成分的反射分量r(x,y)和对应低频成分的照射分量i(x,y),其公式如下:
S(x,y)=r(x,y)·i(x,y)
(1)
式中:S(x,y)为要处理的图像;r(x,y)为反射分量,代表图像边缘细节;i(x,y)为照射分量,描述图像大范围信息。由于式(1)的乘积是不可分的,故对式(1)两边取对数得:
S′(x,y)=lnS(x,y)=lnr(x,y)+lni(x,y)
(2)
式(2)的频域表达式为:
S(U,V)=R(U,V)+I(U,V)
(3)
对式(3)两边用滤波函数处理得:
S(U,V)·H(U,V)=R(U,V)·H(U,V)+
I(U,V)·H(U,V)
(4)
这样反射分量与照射分量就可以分离,从而可以实现减少照射分量、增强反射分量的目的,其中H(U,V)称为同态滤波的传递函数。
对式(4)两边进行傅里叶逆变换得:
hs(x,y)=hr(x,y)+hi(x,y)
(5)
式(5)两边同时取指数得:
ehs(x,y)=ehr(x,y)+ehi(x,y)
(6)
ehs(x,y)即是同态滤波后的图像。决定整个滤波效果的关键在于滤波器的选择即传递函数H(U,V)的选择。
通常传递函数H(U,V)采用巴特沃斯型、高斯型和指数型的来作为同态滤波算法的传递函数。传统巴特沃斯型同态滤波传递函数为:
(7)
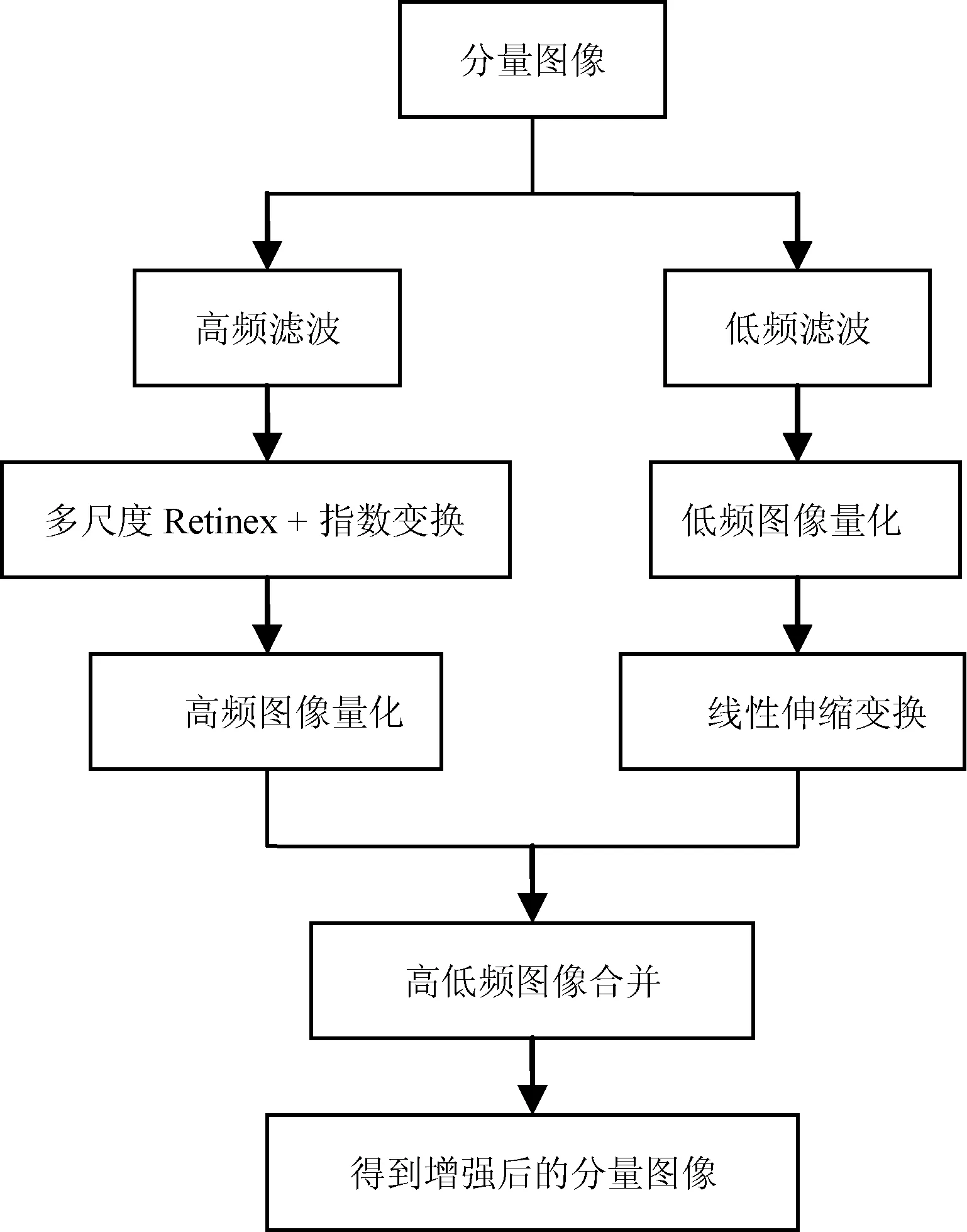
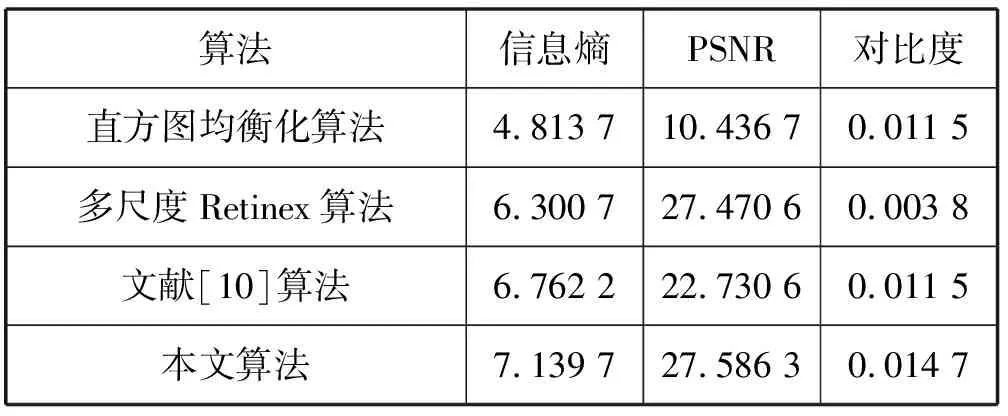
式中:rH表示高频成分增加的倍数,rL表示低频成分增加的倍数,且rL<1 由于传统同态滤波的传递函数参数过多,不易控制,故文献[7]提出一种改进的传递函数模型以获得更多的高频成分。 改进同态滤波函数传递函数为: (8) 式(8)中的参数t控制高频阻带变换率,只要对参数t进行控制,便能够获得理想的滤波效果。 单尺度Retinex算法(SSR)[11-12]的基本思路是:构建高斯环绕函数后,利用高斯环绕函数分别对图像的三个色彩通道(R、G、B)进行滤波,则滤波后的图像就是我们所估计的光照分量;再在对数域中对原始图像和光照分量进行相减得到反射分量,反射分量作为输出结果图像。该算法能压缩图像的动态范围,一定程度上保持图像的颜色和细节的增强。SSR算法公式如下: Ri(x,y)=log(Si(x,y)-log[Si(x,y)*F(x,y)] (9) 单尺度Retinex算法(SSR)中尺度常量σ取值越小,则高斯核模板半径越小,领域范围越小,特定像素受周围像素影响越大,对比度越大,失真可能更严重,同时σ越大也不行,因此σ很难控制。 针对单尺度Retinex算法(SSR)的σ难控制的缺点,多尺度的Retinex算法(MSR)[13-15]被提出,后者能够兼顾到色调再现和动态范围压缩两个特性。与单尺度Retinex算法(SSR)相似,它是对单尺度Retinex算法的加权平均的结果,算法公式如下: log[Si(x,y)*Fk(x,y)]) (10) 低照度彩色图像处理算法一般采用同态滤波算法来得到图像的高频成分,之后再去做其他增强处理,但这样做可能会丢失部分低频成分的信息。为了不仅获得高频成分,还要获得部分低频成分,本文提出了同态高低通滤波算法,之后对高低频图像分别进行增强处理,以达到增强低照度图像的目的。 本文将文献[7]的传递函数作为高通滤波传递函数: (11) 传统的巴特沃斯低通滤波函数为: (12) 传统低通滤波中阶数n越大,出现振铃现象越明显,且传统的低通滤波函数参数不止一个,为了减少参数设置和避免振铃现象,本文低通滤波传递函数设为: (13) 其中只有一个调节参数d0控制低频截止频率,减少参数过多带来的不便。 由多尺度Retinex算法的基本原理可知,利用多尺度Retinex算法可进一步的提取图像细节,文献[5,14]也是结合多尺度Retinex算法来增强图像。因此,本文对高频图像也采用多尺度Retinex算法,考虑到一般多尺度Retinex算法得到对数域的图像整体偏暗,本文将通过指数变换来扩展高灰度级、压缩低灰度级,并经过量化处理得到比较清晰图像。 对于低频图像,考虑到一般亮度较大的图像可以通过量化处理来降低亮度,因此本文对低频图像也进行量化操作,并通过调节线性伸缩变换参数p来改善线性伸缩变换的性能,防止低频图像的过度失真,从而获得最佳效果。 根据上述改进算法的思路,具体的实施方案如下: 1) 对输入的彩色图像S(x,y)进行颜色分离,得到R、G、B三个分量的图像R(:,:,1)、G(:,:,2)、B(:,:,3)。 2) 利用本文所采取的同态高低通滤波分别对分量图像进行处理,得到各分量高低频图像,RH(:,:,1)、GH(:,:,2)、BH(:,:,3)、RL(:,:,1)、GL(:,:,2)、BL(:,:,3)。其中控制高频阻带变换率的参数t取值范围一般为(0,0.01],低频截止频率d0为[5,15]。 3) 对各分量高频图像进行多尺度Retinex算法、指数变换和量化处理,得到处理后的三幅高频图像RH1(:,:,1)、GH1(:,:,2)、BH1(:,:,3)。直接决定图像的输出品质的量化处理公式为: 式中:value为指数变换后的高频图像。 4) 对各分量低频图像先进行量化处理,再对低频图像通过线性伸缩变换参数p进行伸缩变换,得到处理后的三幅低频图像RL1(:,:,1)、GL1(:,:,2)、BL1(:,:,3),其中量化公式与步骤3)量化处理相同,value为低通滤波后的低频图像。本文对线性伸缩变换参数p取值范围为(0,8],越黑暗条件下,取值越小。 5) 合并高低频图像,得到处理后的三个分量图像。 上述步骤的分量图像处理流程如图1所示。 图1 分量图像处理流程 实验是在Intel(R)Core( TM)i5-5200U CPU @ 2.20 GHz ,内存为4.00 GB,操作系统为Window 8.1中文版系统,采用MATLAB 2016a进行仿真实验。选取四幅低照度图像,采用直方图均衡化算法、多尺度Retinex算法、文献[10]算法与本文算法进行仿真实验,实验结果如图2-图5所示,其中(a)是原图,(b)、(c)、(d)、(e)分别是直方图均衡化算法、多尺度Retinex算法、文献[10]算法和本文算法增强图。 图2 走廊原图与算法增强图 图3 饼干盒原图与算法增强图 图4 街道原图与算法增强图 图5 树木原图与算法增强图 人眼观察可以直观反映图像的增强效果,通过人眼可以对一幅图像的亮度显示细节、视觉效果等方面进行主观评价。 由图2可以看出,对于昏暗走廊图,直方图均衡化算法存在过度增强,出现失真问题;而多尺度Retinex算法整体偏暗,部分细节没有展现;文献[10]算法较多尺度Retinex算法整体明朗,但墙壁、房顶架构、地面没有清晰显示;本文算法整体明亮,墙壁、门窗、房顶架构容易观察到,包含的信息更多,亮度也更好。 由图3可以看出,对于低照度饼干盒图,直方图均衡化算法虽然整体柔和,但边缘细节不够突出,同时多尺度Retinex算法出现光晕现象,整体也较暗;文献[10]算法虽然改善了图片视觉效果,整体符合人眼特性,但整体仍偏暗,细节显示不够清晰;本文算法整体明朗,清晰度更高。 由图4可以看出,对于夜晚街道图,直方图均衡化算法过度增强,噪声很大,多尺度Retinex算法,强调了局部,整体细节没有显示;文献[10]算法较多尺度Retinex算法亮度有所提高,左侧高层房屋以及右侧远处的树木没有很好体现;本文算法整体亮度提高,两旁树木及房屋细节也被体现出来。 由图5可以看出,对于黑暗树木图,直方图均衡化算法处理后图像偏白,整体像蒙上一层雾,视觉效果不佳,对于多尺度Retinex算法,近处两旁的树木有所体现,地面的亮度也有所增强,但也是局部体现,远处的细节也没有展现,如远处的人;文献[10]算法较多尺度Retinex算法细节凸显得更多,但只是局部区域的对比度增强;而本文算法左右两边的树能看得更远,远处的细节更多,整体更亮。 图像增强效果的客观质量评价标准一般有信息熵、峰值信噪比(PSNR)和对比度三个客观指标。信息熵反映图像信息量大小,其值越大,则图像信息越丰富,细节保持越好。峰值信噪比(PSNR)表示一个信号的最大功率与可能影响其噪声功率的比值,PSNR越大,失真度就越小。对比度能够较好地反映视觉效果,值越大,则图像越清晰醒目。 四幅低照度图像下几种算法的信息熵、峰值信噪比和对比度值如表1-表4所示。 表1 图2的各算法客观质量评价 表2 图3的各算法客观质量评价 表3 图4的各算法客观质量评价 表4 图5的各算法客观质量评价 可以看出,本文算法在信息熵上都优于其他几种算法;表1-表4中本文算法较性能较好的文献[10]算法信息熵分别提高了0.377 5、0.798 1、0.870 8、0.736 7,即百分比提高约为5.6%、12.3%、13.6%、11.9%,表明在图像细节与含有的信息程度上较其他两种算法更突出、更丰富;在峰值信噪比中,本文算法较文献[10]算法,最低提高了4.797 6,百分比为31.1%(表3),即图像的失真程度较其他两种算法低;从对比度上来看,本文算法较文献[10]算法,最低提高了0.002 1,百分比约为24.1%(表2),表明图像整体清晰,很大程度上改变了原来低照度图像昏暗、不清晰的状态。 同态滤波算法虽然可以消除图像照明不均,增强暗区的细节和不损失亮区细节的特点,但对于较黑暗下的图片,整体处于偏暗状态,仍然很多细节不能表达出来,同时多尺度Retinex算法会出现光晕等现象。因此,本文采用同态高通滤波、多尺度Retinex算法、量化与同态低通滤波、线性伸缩变换和量化相结合的处理方法,使得低照度图像亮度更好,清晰度更高,细节更突出。实验证明了本文算法在主观评价与客观性能上都优于其他两种对比算法,具有更加有效的增强低照度图像的性能。2 Retinex算法
2.1 单尺度Retinex算法
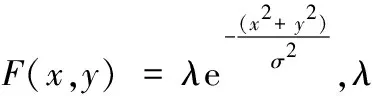
2.2 多尺度Retinex算法
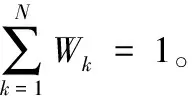
3 算法设计
4 算法方案
5 实 验
5.1 实验仿真条件及结果





5.2 主观评价
5.3 客观评价
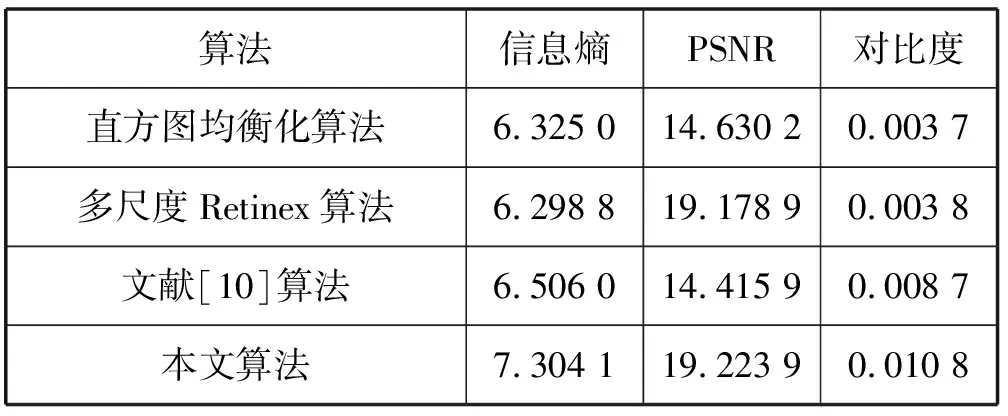
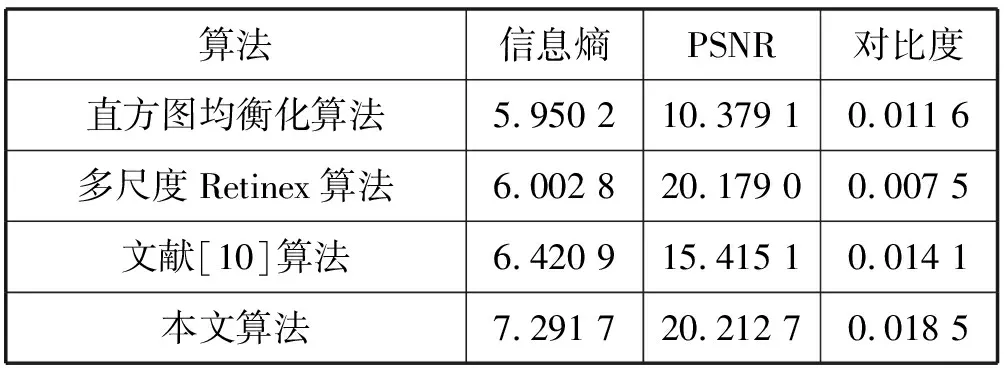
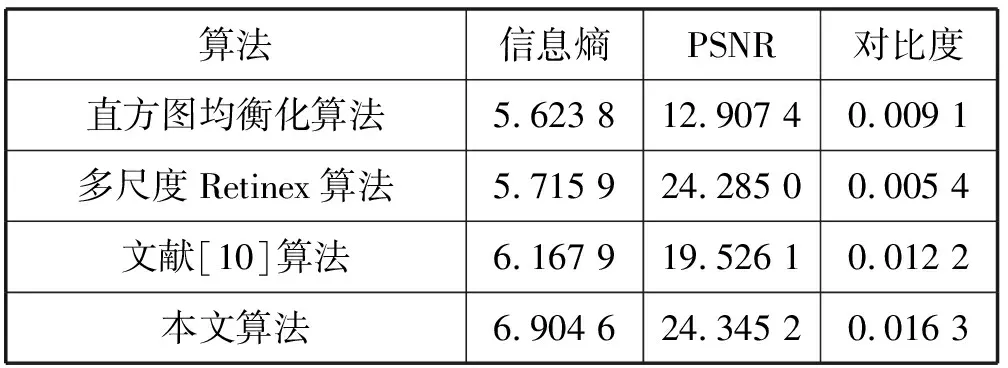
6 结 语

