发动机机队备发仿真研究
赵洪利 张 猛
(中国民航大学航空工程学院 天津 300300)
0 引 言
为了保障飞机的正常运行,航空公司必须为飞机配备一定量的备件,但这会带来高额的成本,大约占飞机运营成本的10%左右[1]。作为最为昂贵的备件——备用发动机(备发)的数量一直是航空公司重点关注的问题,备发数量过多会带来巨额的保障成本,阻碍航空公司的现金流动;备发数量过少会造成飞机停场(AOG)等一系列问题,从而影响航空公司的正常运营。因此适当的备发数量对实现最大化备发利用率和最小化保障成本至关重要[2]。
目前,备发率一般是航空公司用来衡量备发数量的一个重要指标,是指该机队中的备发数量与机队在翼发动机总数的比值。就备发数量的计算问题,大致可分为三种方法:(1) 基于统计学理论:陈凤腾等[3]使用改进的比率危险模型,结合高斯公式计算了备发数量;白芳等[4]同样使用高斯公式计算了备发数量,通过维修保障成本模型优化了备发数。(2) 基于算法:赵洪利等[5]基于间隔控制算法,通过固定备发数量得出了其对应的缺少发动机(缺发)时间,并验证了算法的优越性;Sheng等[6]采用遗传算法,通过仿真寻优找到了机队备件供应的最优解决方案以及最小化成本。(3) 基于经验公式:GE公司结合返厂率(即返厂次数与飞行时间的比值)、周转周期(即发动机维修所用的时间)等一系列因素,给出了计算备发数量的经验公式。
但是以上方法均存在考虑发动机下发因素单一,无法给出确切的备发规划等问题,必然会对最终结果产生影响。针对以上问题,本文使用离散事件仿真的方法,利用MATLAB软件建立了备发仿真模型。基于排队论思想,采用固定增量的时间推进机制,在先进先出排队规则下,考虑维修厂(Maintenance, Repair and Overhaul, MRO)维修能力的限制,以每三年为一个规划期为机队制定了15年的备发规划。
1 备发仿真模型设计
1.1 模型基本假设
为准确地展现发动机“在翼—下发—在翼”的使用流程,在建立仿真模型之前需做出一些基本假设。
假设1:发动机在使用过程中存在性能衰退、硬件损伤与偶然性损伤多种下发因素,各因素相互独立,且故障时间服从一定分布。
假设2:发动机性能恢复视为非完美维修,性能恢复后发动机排气温度裕度(Exhaust Gas Temperature Margin,EGTM)服从一定分布。
假设3:若有缺发的情况发生,采取租赁发动机的方式保障航空公司正常运营。
假设4:MRO维修发动机时,采取先进先出的维修排队机制。
1.2 输入输出模型参数
基于以上所有假设,建立备发仿真模型,模型输入输出参数包括:
(1) 机队规模:假设机队中共25架全新双发飞机共50台发动机,且分梯次引进机队,每10天引进一架。
(2) 使用情况:根据某航空公司实际使用情况,设定飞机一天运行5循环,一年运行1 800循环,使用寿命为15年。
(3) 周转周期与MRO维修能力:发动机周转周期为75天且MRO可同时维修10台发动机。
(4) 备发数量:备发数量起始设为1台,若不能满足保障率要求时增加备发数量。
模型输出参数包括:
(1) 总缺发时间Tlack。
(2) 各规划期的保障率ω:
(1)
式中:M为机队发动机数量;P为规划期长度;Tlack1是各规划期内的缺发时间。
1.3 仿真方法与流程
离散事件仿真系统是状态仅在离散时间点上发生变化的仿真方法。事件被初始化后,通过处理在仿真时间轴上不连续点处发生的带有时间戳的事件,进行所有特定计算。所使用的MATLAB软件是一款强大的数学计算软件,已被广泛地运用在算法开发、程序编写等方面。在MATLAB仿真平台上,利用.m文件进行程序编写,建立离散事件备发仿真模型,流程如图1所示。
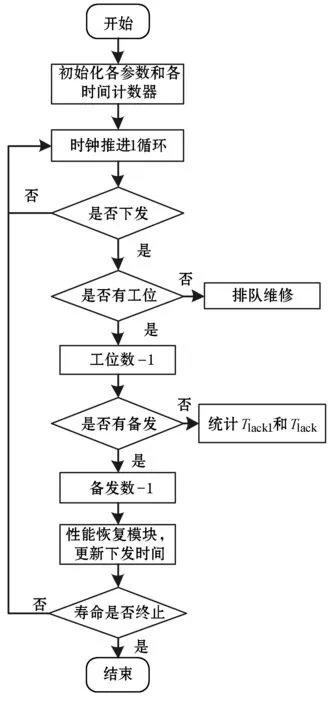
图1 备发仿真流程
(1) 初始化各项输入参数、Tlack计数器和Tlack1计数器。
(2) 编写性能衰退、硬件损伤和偶然性损伤三种下发因素随机数产生函数并调用,使用sort函数将产生的随机数排序,给定机队所有发动机故障下发时间戳。
(3) 时钟推进1个循环,遍历所有发动机判断是否到达下发时间戳。若是,再次推进1个循环;若否,发动机进厂维修并判断MRO工位情况。同时使用switch函数判断故障类型并记录。
(4) 若MRO有工位,则工位数-1,判断备发情况;若MRO无工位,发动机排队等待工位出现。
(5) 若有备发,则备发数-1,重新产生故障下发时间,并判断发动机寿命情况;若无备发,记录缺发开始时刻。等待维修完成后,记录缺发结束时刻,并统计缺发时间Tlack。
(6) 若寿命不终止,时钟再次推进1个循环;若终止,输出各规划期保障率和总缺发时间Tlack,单次仿真结束,输出故障记录。
(7) 多次重复仿真,使用plot函数作图查看各规划期内的保障率平均收敛情况。经测试,仿真次数为500次时收敛情况较好。
2 下发策略与性能恢复
导致发动机下发的因素是很复杂的,本文考虑发动机的性能衰退、硬件损伤和偶然性损伤三种主要因素竞争下发,即单次发动机下发时间戳t为:
t=min{t1,t2,t3}
(2)
式中:t1为性能衰退下发时间随机数;t2为硬件损伤下发时间随机数;t3为偶然性损伤下发时间随机数。
2.1 性能衰退伪随机数
2.1.1性能衰退模型建立
发动机的性能衰退,一般会在发动机EGTM的衰退情况上有所反映。EGTM定义为发动机排气温度(Exhaust Gas Temperature,EGT)红线值与在海平面拐点温度下全功率起飞时的EGT之差[7]。随着发动机的使用, EGTM值会逐渐减小直至到达警戒值。本文将采用随机wiener过程,对发动机EGTM衰退过程建模。
发动机EGTM在t时刻的衰退量为X(t),假设该衰退量服从wiener过程{X(t),t≥0}有:
X(t)=X(0)+λt+σB(t)
(3)
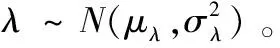
T=inf{t1|X(t1)≥Df}
(4)
式中:Df=S-L,Df是EGTM衰退阈值,S是发动机EGTM的起始数值,L是EGTM的警戒值;t1是故障下发时间;inf表示集合的下限值。此时该随机wiener过程的失效函数为[9]:
(5)
式中:Φ表示标准正态分布的累积概率密度函数。
2.1.2模型参数计算与伪随机数生成
表1是某航空公司机队10台某系列发动机实际使用过程中的EGTM衰退数据。
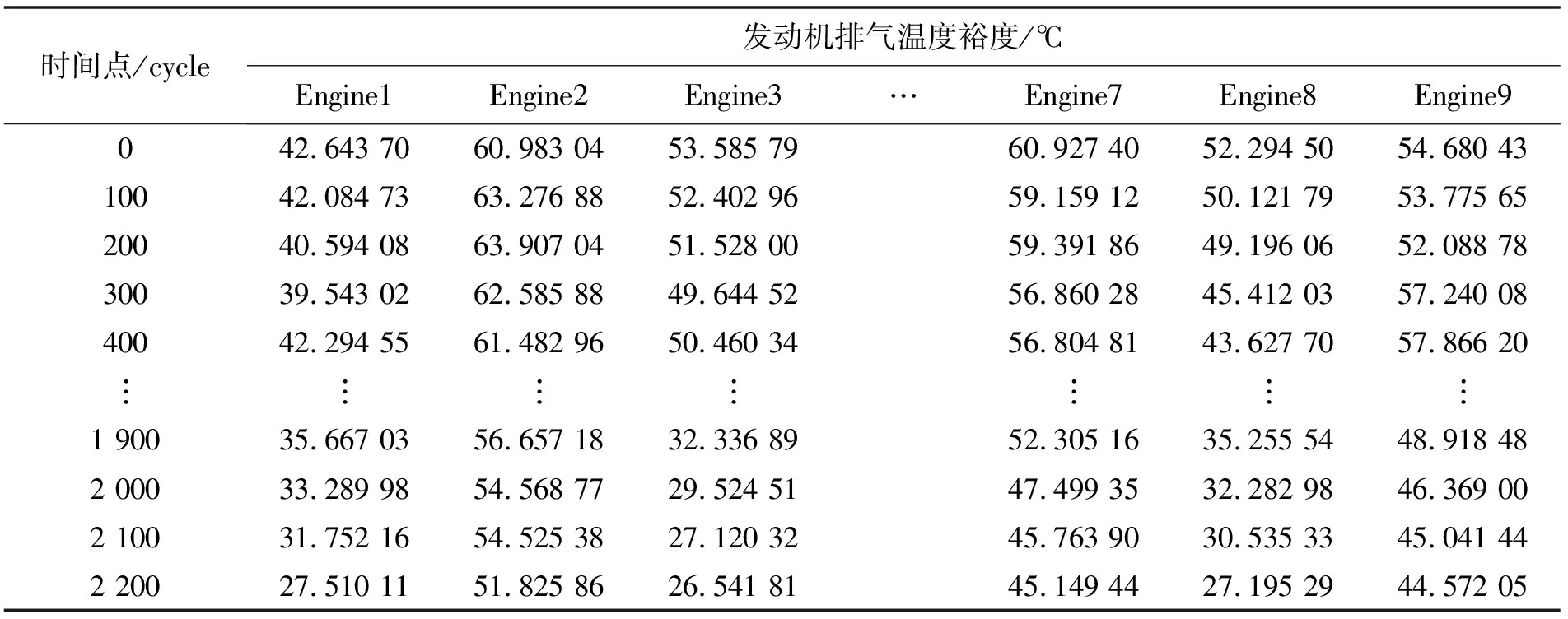
表1 某机队发动机EGTM样本数据

由于该随机wiener过程的失效函数较为复杂,难以直接生成符合该函数的随机数,本文采用牛顿迭代法求解性能衰退下发时间。牛顿法是一种用来求非线性方程解的迭代算法,在给定初值合理的情况下,可以很快求解出方程解[11],本文中所用迭代公式如下:
(6)
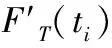
2.2 硬件损伤伪随机数
2.2.1硬件损伤模型建立
航空发动机在使用过程中,主要的故障包括低周疲劳、热机械疲劳、蠕变、腐蚀等[12],这些损伤通常会损耗部件寿命,造成发动机下发。本文采用威布尔分布来表征该种故障的发生,其失效函数为:
(7)
式中:t2为故障时间;β为形状参数;η为尺度参数。
2.2.2模型参数计算与伪随机数生成
根据某机队发动机实际下发数据显示,发动机硬件损伤常见的故障分为三种:高压压气机(HPC)叶片损伤、燃烧室(Combustor)损伤和高压涡轮(HPT)一级叶片损伤,分别提取故障下发时间如表2所示。
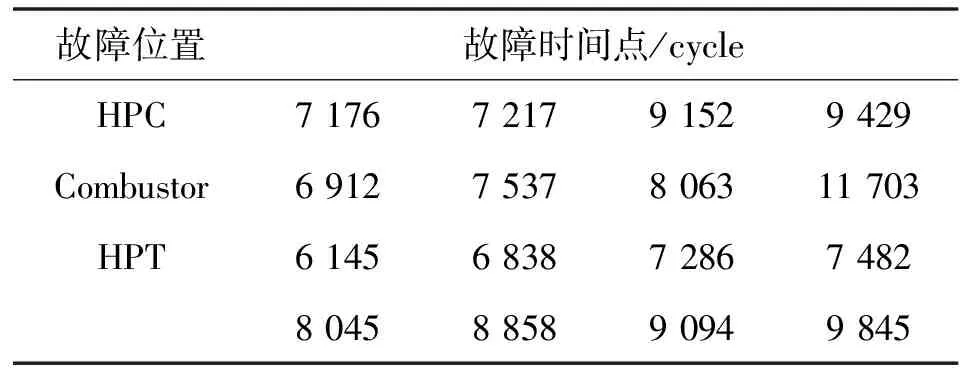
表2 实际发动机下发时间
根据表2中数据采用中位秩回归参数估计法估算模型参数,结果如表3所示。
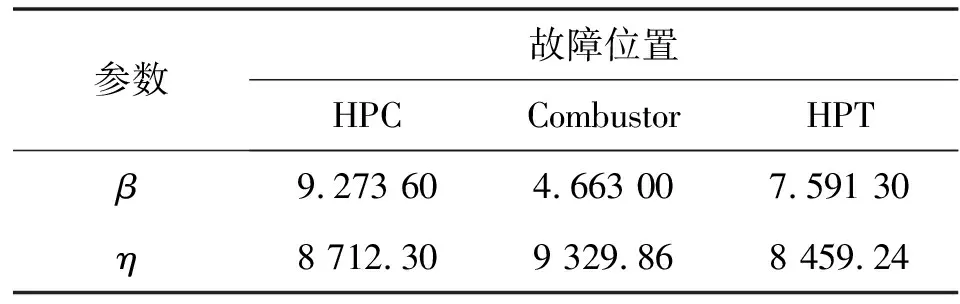
表3 模型参数
使用反变换法,计算威布尔分布的失效时间t2为:
(8)
式中:F(t2)是区间[0,1]内的均匀分布随机数,同样由rand函数产生,计算生成一系列硬件损伤下发时间伪随机数t2。
2.3 偶然性损伤伪随机数
2.3.1偶然性损伤模型建立
发动机的偶然性损伤,是指发动机在使用过程中由于鸟击、雷击等突发事件,造成发动机故障下发,且这类故障具有无记忆性的特点。所以本文采用指数分布模型,对发动机偶然性损伤下发时间建模,其失效函数为:
F(t3)=1-exp(-λ3t3)
(9)
式中:t3为故障时间点;λ3为故障率。
2.3.2模型参数计算与伪随机数生成
根据最新的《鸟击航空器信息分析报告》,能够造成发动机下发的偶然性损伤故障率λ3=4.335×10-6/cycle。
同样使用反变换法,生成偶然性损伤下发时间伪随机数t3,具体过程如上文,这里不再赘述。
2.4 性能恢复EGTM衰退阈值伪随机数
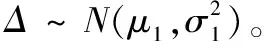
(10)
(11)
式中:c为修正系数,保证Δ在区间[0,Df]内累积概率为1;F(Δ)为该截断正态分布的累积概率。
采用正态分布拟合该型号发动机性能恢复后EGTM衰退阈值Δ具体如表4所示,根据式(10)计算c=1.015。同样使用牛顿法,迭代计算性能恢复后EGTM衰退阈值伪随机数。
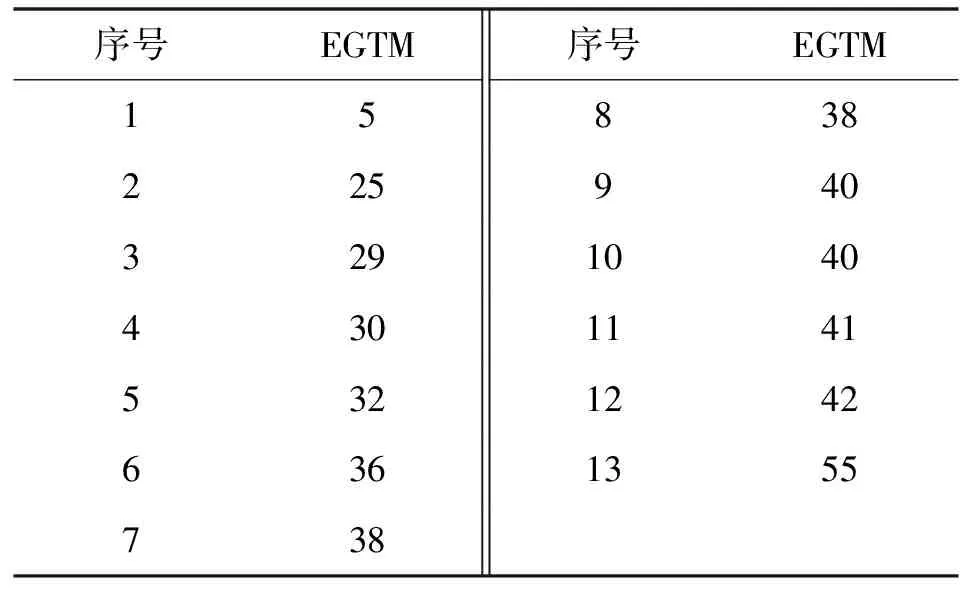
表4 性能恢复后EGTM衰退阈值
3 模型验证
图2是做500仿真的平均总缺发时间点,该值收敛于45 100循环。由于总缺发时间点直接影响保障率大小,所以这里对假设H0:Tlack=45 100 cycle做t检验,以验证模型的正确性。
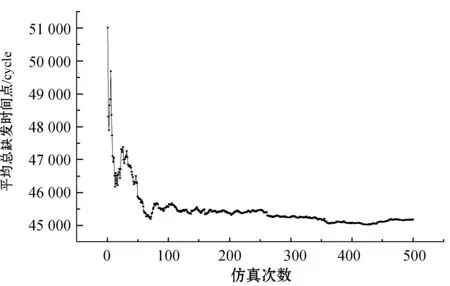
图2 平均总缺发时间点仿真结果
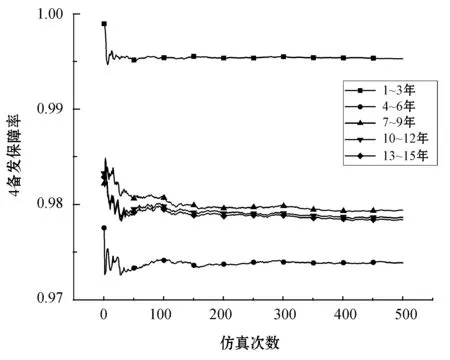
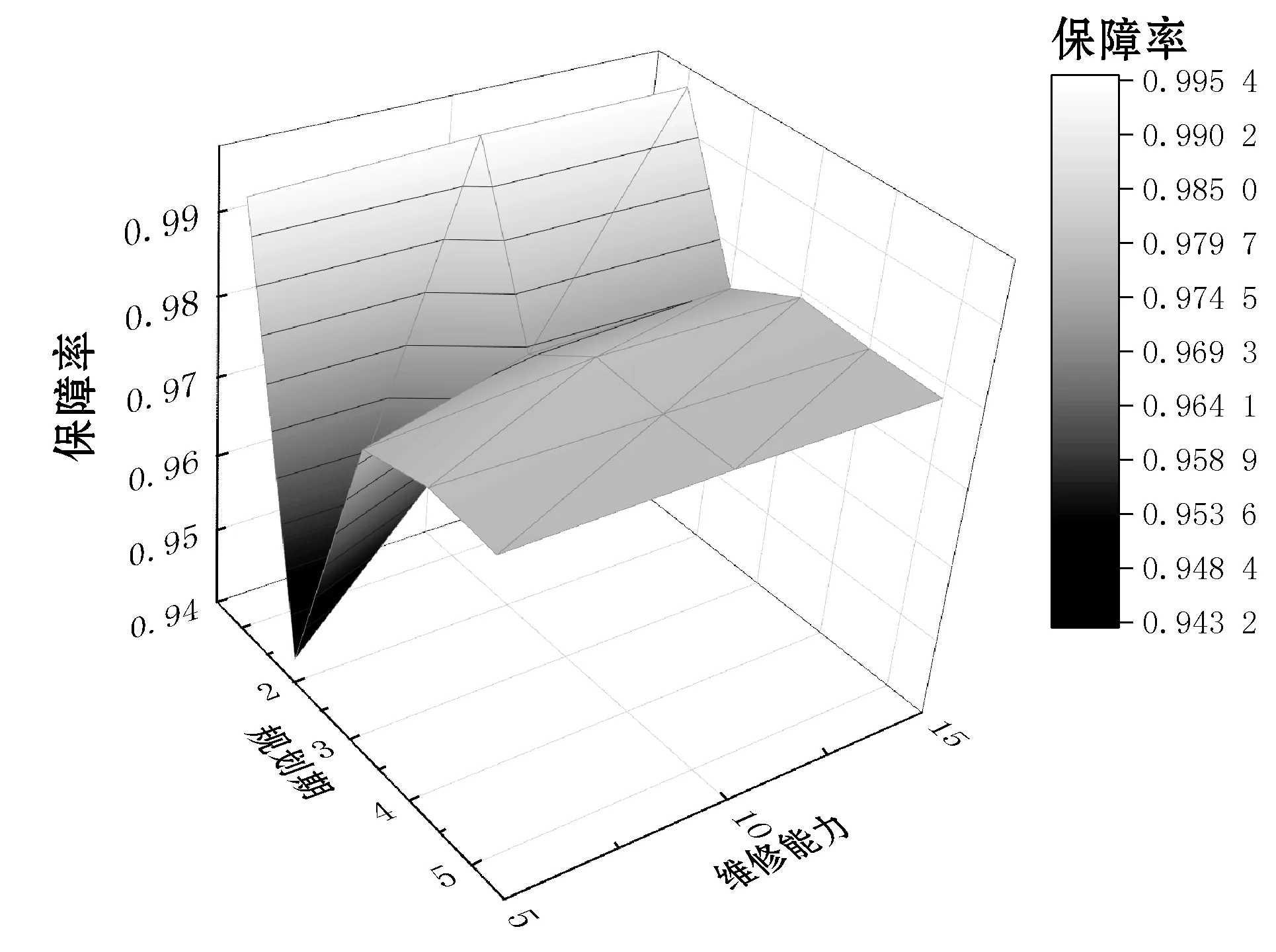
重新仿真产生10组Tlack数据如表5所示,取置信度为95%,双边检验临界值t0.025,9=2.26。经计算t0=2.008 表5 10次Tlack抽样数据 一般航空公司对于保障率的要求在95%~97%之间[15]。本文取97%的保障率标准,1台备发时各规划期内的保障率仿真结果如图3所示。 图3 1台备发保障率仿真结果 仿真结果显示,1台备发只能满足1~3年内的机队运营,其余规划期内保障率均在97%以下。想要满足整个寿命阶段的保障率要求必须要增加备发数量,因此依次增加备发数量重新仿真,结果如图4-图6所示。 图4 2台备发保障率仿真结果 图5 3台备发保障率仿真结果 图6 4台备发保障率仿真结果 依据以上所有仿真结果,当4台备发时满足各阶段的保障率要求,现给出各个规划期内的最佳备发数如表6所示。 表6 各规划期内最佳备发数量 由于1~3年属于发动机的首次寿命阶段,发动机在翼时间相对较长,因此少有下发,仅需要1台备发;4~6年内,由于发动机初始寿命不够分散,发动机的首次下发多发生在该阶段,出现集中下发的现象,因此所需备发数量最多为4台;7~15年内,发动机已进入成熟期,各阶段下发次数以及发动机在翼时间已接近稳定,因此保障率几乎维持不变,所需备发数也减少至3台。 目前航空公司的备发率一般维持在5%~8%。对比本文最多备发数为4台即备发率为8%的仿真结果,具有合理性,且减少了1~3年备发数量过多造成的成本浪费,4~6年也可以在购买3台备发的基础上额外租发1台以满足备发需求,使备发规划更为灵活。 设定备发数量为4台,将MRO维修能力改为5台和15台,对比维修能力为10台时各规划期的保障率,具体结果如图7所示。 图7 维修能力敏感度分析图 由图7可得出以下结论: (1) 当维修能力为5台时,第2个规划期即4~6年的保障率很低,小于维修能力为10台和15台同阶段保障率,说明5台的维修能力是不能满足该机队的维修需求的。 (2) 维修能力为10台和15台在各个规划期内的保障率相差都不大,因此10台的维修能力即可满足该机队的维修需求,工位不够而出现维修等待的现象很少发生。 本文采用离散系统仿真的方法,依据排队理论建立了备发仿真模型。分规划期给出了机队15年内不同时间段的最佳备发数量,使备发规划更加细致准确且灵活,减少了备发数量过多造成的成本浪费,同时对MRO的维修能力进行评估。对比航空公司现行的备发率,本文结论较为准确。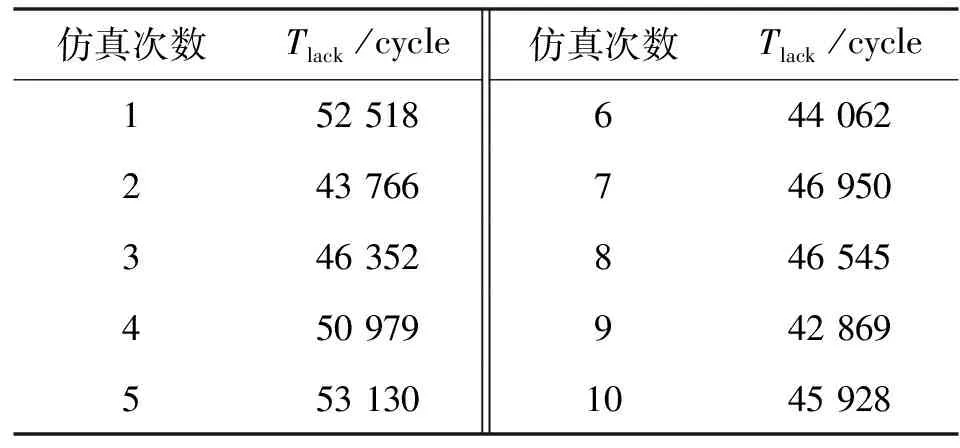
4 仿真结果与分析
4.1 仿真结果
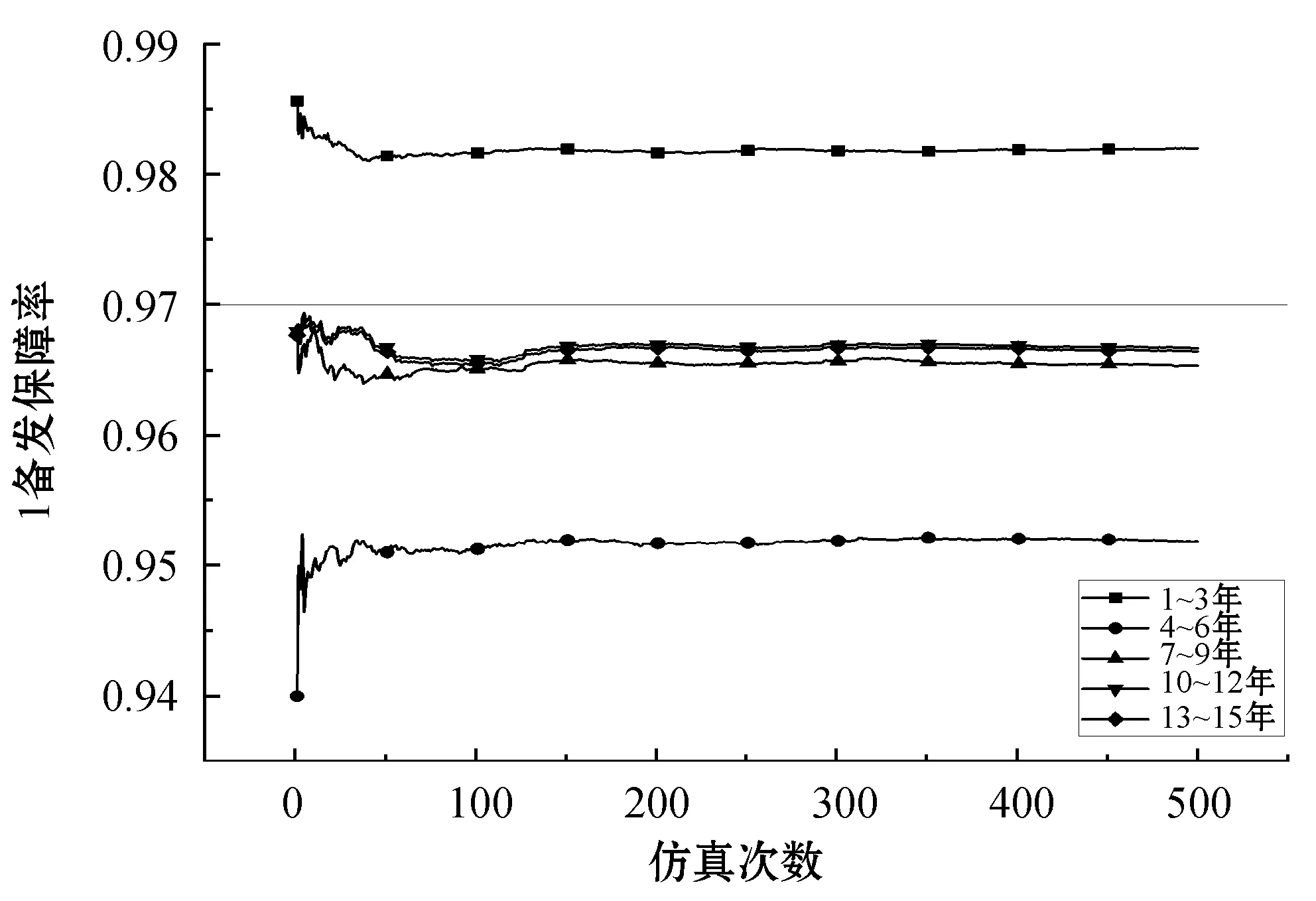
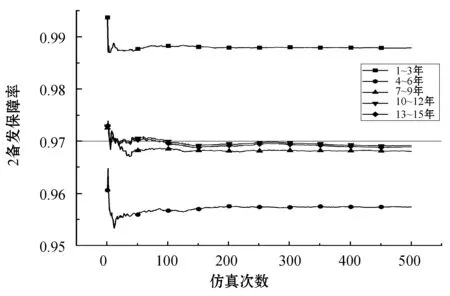


4.2 结果分析
4.3 维修能力敏感度分析
5 结 语

