由一道热学高考题引发的对气体压强微观机制的思考

◇ 广东 周 攀 蔡 钳

气体压强的微观解释是物理教学的难点．本文通过对一道全国高考热学试题的探讨、变式和思考,对气体压强变化的微观机制进行深入分析、推导和讨论,论证压强变化的本质原因,进一步讨论压强变化与单位时间碰撞单位面积器壁的分子数的相关性．

例(2014 年全国卷Ⅰ理综第33题)一定量的理想气体从状态a 开始,经历三个过程ab、bc、ca 回到原状态,其p-T 图象如图1所示．下列判断正确的是( )．

A．过程ab 中气体一定吸热

B．过程bc 中气体既不吸热也不放热

C．过程ca 中外界对气体所做的功等于气体所放的热

D．a、b 和c 三个状态中,状态a 分子的平均动能最小

E．b 和c 两个状态中,容器壁单位面积单位时间内受到气体分子撞击的次数不同

图1

我们主要看该题的选项E,b 和c 两个状态,温度相同,即分子的平均动能相等,单个分子对容器壁的平均撞击力相等,状态b 压强比状态c 大,可判断状态b 单位时间内容器壁受到分子撞击的次数多．温度相同情况下,通过压强大小关系可推知容器壁单位面积单位时间内受到气体撞击次数的大小关系．

变式下列说法正确的是( )．

A．布朗运动虽不是分子运动,但它证明了组成固体颗粒的分子在做无规则运动

B．一木块被举高,组成该木块的所有分子势能都增大

C．当液体与大气接触时,液体表面层分子的势能比液体内部分子的要大

D．缓慢压缩一定量气体,若此过程气体温度保持不变,则外界对气体做正功,但气体内能不变

E．气体体积不变时,温度越高,单位时间内容器单位面积受到气体分子撞击次数越多

该题的选项E 中,气体体积不变,所以分子数密度不变;温度越高,分子平均动能越大,此时单位时间内容器单位面积受到气体分子撞击的次数越多,因此气体压强变大．

上述两个问题都采用了逆向思维:从宏观的压强变化去判断微观的原因．宏观的压强变化“触手可及”,反推微观原因,无可厚非．但思维发散的学生提出了这样一个问题:有没有可能存在压强变大,单位时间碰撞单位器壁的分子数变少的情况呢?

人教版高中物理教材《选修3-3》中指出气体压强的大小跟两个因素有关:一个是气体分子的平均动能;另一个是分子的密集程度．那么压强与容器壁单位面积单位时间内受到气体撞击的次数(以下简称“碰壁数”)之间有什么关系呢? 通过对气体压强的直观认识,可以知道压强由单个分子对容器壁的平均撞击力和容器壁的碰壁数来决定．单个分子对容器壁的平均撞击力与分子的平均速率有关,即与分子的平均动能有关．碰壁数除了与分子的平均速率(或者说平均动能)有关,还与气体分子的密集程度,即分子数密度有关．

基于这个思考,可将学生的问题加上一定的条件分解为两个问题．问题1:分子平均速率增大,分子数密度减小时,如果压强增大,此时碰壁数一定增加吗?问题2:分子平均速率减小,分子数密度增大时,如果压强增大,此时的碰壁数一定增加吗?

对于问题1,可以尝试进行这样的推理:假设一定质量的气体历经等压膨胀过程,体积增大,分子数密度减小;温度升高,分子平均速率增大;为了维持压强不变,碰壁数必须减小．那么,可以猜想在等压膨胀的基础上,保持体积不变,温度再稍微升高一点,压强增大,此时碰壁数仍然有可能小于等压膨胀前的碰壁数．

为了定量研究压强与碰壁数的关系,我们可以从理论上来推导压强p 和碰壁数Γ 分别与分子平均速率和分子数密度n 之间的关系．可以推导出压强

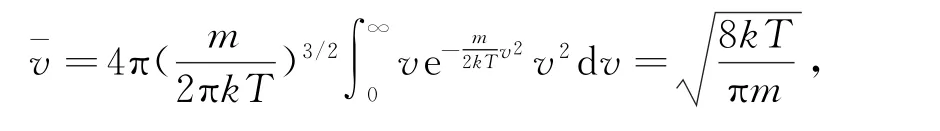
速率平方的平均值为

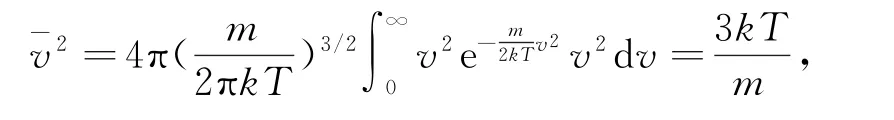
表1

从上述讨论中可以看到,压强和碰壁数均由分子数密度、分子平均速率共同决定,但是当分子数密度增大、压强增大时,碰壁数一定增大;当分子数密度减小、压强增大时,碰壁数可能增大也可能减小．