考虑互惠偏好的闭环供应链合作博弈模型
兰龙辉,郑小雪,李登峰,曾婷婷
(1.福州大学 经济与管理学院,福建 福州 350108;2.闽江学院 新华都商学院,福建 福州 350108;3.电子科技大学 经济与管理学院,四川 成都 611731)
0 引言
工业革命以来,人类的现代化步伐不断加快,导致环境污染、全球气候变暖等问题日益突出,随着人们对可持续发展战略的认可,越来越多的企业纷纷向着环境友好型转型,回收废旧品再制造已经成为制造企业的转型方向,企业的供应链也需做出相应的改变。一个设计良好的闭环供应链系统不仅会影响企业的利润,还影响着企业未来的发展。过去建立的供应链协调系统,大多都是基于参与者是理性的前提下进行的,这样容易导致双重边际效应,无法达到协调供应链的目的。
近年来,国内外学者纷纷投入对闭环供应链系统的设计中,并取得了不错的成果。易余胤[1]通过建立基于Stackelberg博弈以及Nash均衡的3种博弈模型,表明供应链的渠道利润和各个成员的利润会受到不同市场主导模式的影响。Leng等[2]在一个三级供应链中考虑需求信息共享下采用合作博弈理论对节约成本进行有效分配,建立了三人合作博弈的特征函数,并推导出使得5种联盟稳定的必要条件,进而为节约成本分摊提供了方案。Ma等[3]在三级闭环供应链中建立了不同的合作模型来分析最优决策和渠道利润,通过对不同联盟结构的比较,表明合作策略有助于产生双赢局面、增加联盟利益,对整个供应链来说是一种获得更高效率的有效途径。Huang等[4]通过建模分析闭环供应链的成员在第三方回收商和零售商存在竞争的双渠道回收环境下,其最优的利润和定价策略。Yoo等[5]通过建立一个由制造商,零售商和再制造商组成的三级供应链模型,提出5种不同的供应链结构模型,通过对不同模型的考虑来提高供应链的利润。
上述研究的前提是个体理性且追求的自身收益最大,但参与个体应该还具有社会偏好,这也导致研究结果和现实世界有所不同。因此将公平、互惠等社会偏好引入闭环供应链的设计中显得十分必要。丁雪峰等[6]研究了公平关切在闭环供应链中对制造商和零售商的影响。Zheng等[7]考虑零售商的公平关切,表明在分散模型和部分联合模型下的渠道利润低于集中模型下的收益。利用合作博弈论,提出了基于Shapley值、核仁解和平等满意度的3种剩余利润分配方案,再经数值仿真证明了该方案同时满足个人理性和集体理性,从而使大联盟得以稳定。Ma等[8]在集中和分散模型的闭环供应链中分别求得供应链的利润,并为供应链中的成员提供了最优定价决策方案,还将模型延伸到考虑零售商的公平关切以及对不同回收模式的成本优势进行对比。除公平关切外,在现实中不难发现,互惠偏好也是普遍存在的。在供应链中,企业由于互惠偏好的影响,会为其他企业提供资金和技术上的支持,让合作企业快速成长,加强供应链间的协作。这种互惠偏好可以加强企业之间的协调,使得整条供应链更具竞争力。因此,将互惠偏好作为参数纳入供应链合作机制设计中符合现实情况,也更具有现实意义。张克勇[9]研究了互惠偏好对闭环供应链系统收益和效率的影响,双方的互惠偏好程度与回收量呈正相关。Du等[10]针对开环供应链系统中零售商具有互惠偏好行为而供应商不具有和双方都具有互惠偏好行为的两种情形,研究了互惠偏好对系统均衡和开环供应链成员决策的影响以及系统协调问题。
综上所述,在对闭环供应链的研究中,较多学者以合作博弈论作为理论基础,合作博弈主要关注多个局中人之间的联盟(coalition)形成方式及联盟效用分配方案;在供应链领域,合作博弈理论主要应用于运作成本分摊和合作收益分配问题。其次,国内外的闭环供应链设计主要集中于市场主导模式、最优定价和利润分配。虽有学者将社会偏好引入研究中,但也大多集中于公平关切和利他偏好,互惠偏好的研究尚未成型,且大部分研究多以二级供应链为切入点,因此将互惠偏好引入多级闭环供应链系统具有重要意义。本文在对闭环供应链研究的基础上,将互惠偏好引入多级闭环供应链,设计其合作机制,帮助供应链成员优化利润,提升整条供应链效率和渠道收益,从而推动制造企业向环境友好型企业转型发展。
1 问题描述与相关假设
本文考虑由一个制造商(M)、一个分销商(D)和一个零售商(R)组成的三级闭环供应链。制造商生产新产品的同时,从消费者手中回收已使用的产品,并将其中一部分或者全部再制成产品,而后零售商将再制品以低于新产品的价格销售。首先,制造商设置新产品和再制品的批发价格后卖给分销商,其次分销商同样设置新产品和再制品的批发价后卖给零售商。最后,零售商定义新产品和再制品的零售价格卖给消费者。本文将上述通过生产、制造、销售新产品,再将废旧品回收再制造、再销售的良性循环供应链定义为闭环供应链。

本文的主要目的是理解具有互惠偏好的合作机制在闭环供应链中对于最优决策和利润分配的意义。因此,本文将Savaskan等[11]的模型扩展成由一个制造商、一个分销商和一个零售商组成的一系列三级闭环供应链模型(如图1),其中包含4个模型,即制造商和分销商合作模型(Model MD)、分销商和零售商合作模型(Model DR)、集中决策模型(Model C)和完全分散模型(Model D)。具体而言,以Model C和Model D作为基准情况,对于每一种情况,本文考察了局中人最优决策和在互惠偏好下的利润。设计了将互惠偏好引入3个合作机制,进而分配因渠道合作带来的最高收益。表1汇集了所用的符号标记,其他主要假设将在下面进行概述和讨论。

表1 参数和决策变量
以下为本研究中的主要假设:
假设1动态问题转换为稳定的One-Period模型。
本文重点关注分销商和零售商的互惠偏好对闭环供应链收益的影响。其他文献,如Liu等[12]将One-Period模型运用于再制造环境中。在本文中,根据Zou等[13]的设想,考虑可回收废旧产品是不受限的,即假设用于再制造产品的已使用商品是充足的。
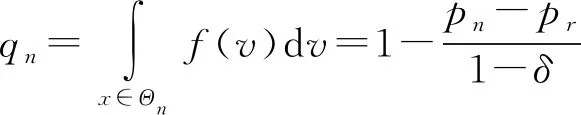
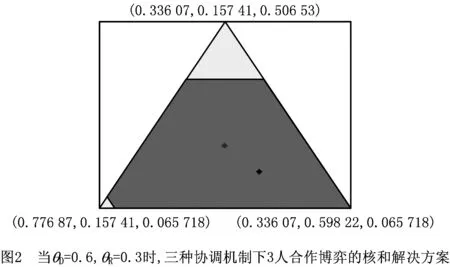
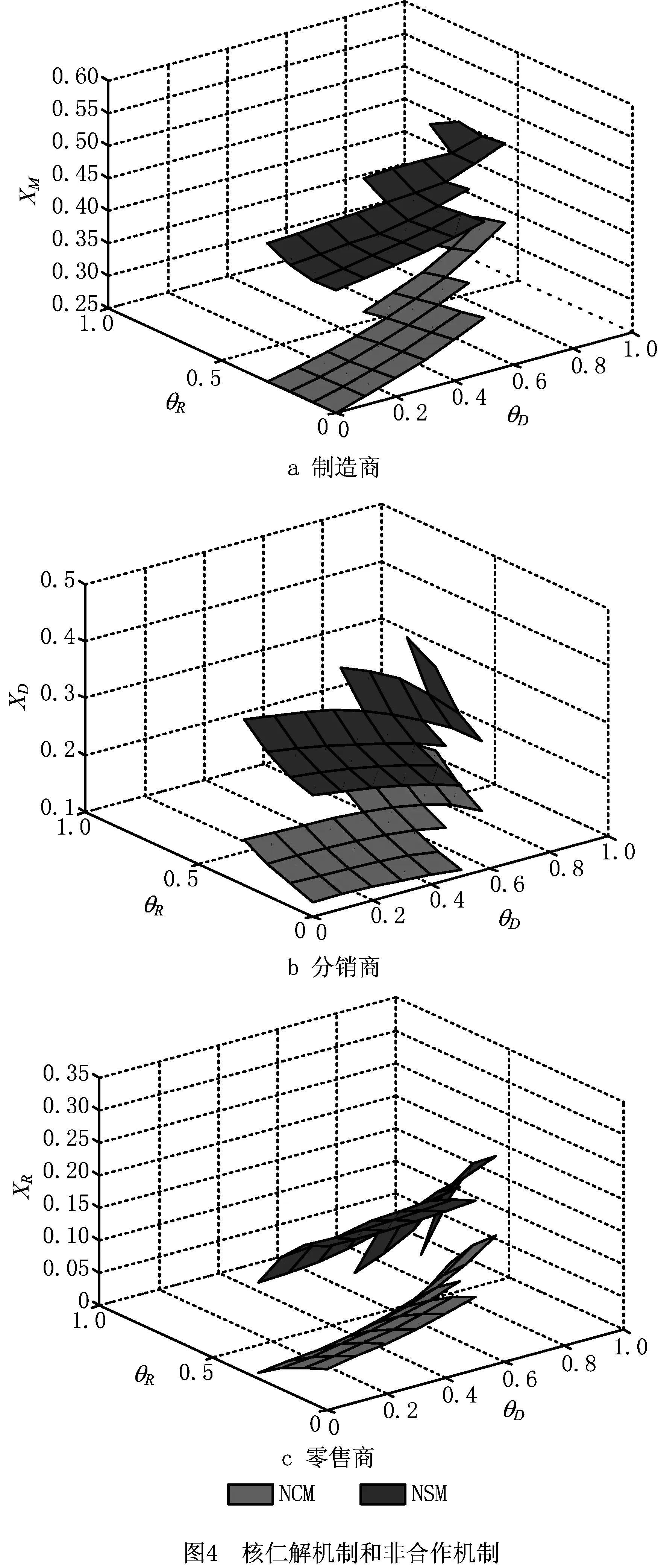
假设3再制造产品的单位制造成本低于新产品,即0 废旧品的回收利用,会使得再制造的过程总是比生产新产品的成本低,即0 假设4为了确保再制造有利可图,假设A+cr<δcn。 由于A+cr<δcn,制造商可以享受再制造成本优势,从而有利于回收和再制造,然后制造商同时生产新产品以及再制品。该活动中有两个主要影响因素:①回收和再制造费用为A+cr;②消费者折扣率δ,当A+cr≥δcn,制造商将不会从事再制造活动。 假设5分销商具有不可替代的分销渠道,使得制造商无论在何种情况下都不能与零售商结盟。 在三级闭环供应链中,上游的制造商、中游分销商和下游的零售商可以两两结盟。但是其中制造商和零售商不能结盟,因为分销商有不可替代的分销渠道,制造商不得不使用他的渠道将产品运送给零售商。Leng等[2]强调供应链中游成员具有不可替代的资源,是不可或缺的环节。 假设6在闭环供应链中,零售商只对它上游的决策者表现出互惠偏好(即成员或联盟),上游成员是否组成联盟,不会影响零售商的互惠偏好。 在闭环供应链分散环境中,零售商只关心其相邻上游成员(即分销商),而不考虑制造商的利润。在闭环供应链部分联盟的环境下,当分销商和零售商组成一个联盟(即DR),零售商表现出对联盟的互惠偏好,而不是对分销商的。值得注意的是,零售商在两种情境中表现出相同程度的互惠偏好。 假设7在闭环供应链中,分销商只对它下游的决策者(即零售商)表现出互惠偏好,与上游制造商联盟时,会影响联盟对零售商的互惠偏好,使得θ(MD)R=εθD,ε∈[0,1],本文中取ε=1的情况。 在闭环供应链分散模型中,分销商只关心其相邻下游成员(即零售商),而不会去考虑制造商的利润,在闭环供应链部分联盟的环境下,当分销商和制造商组成一个联盟(即MD),分销商由于制造商的加入,整个联盟对零售商的互惠偏好会有所下降,因为制造商在闭环供应链中占主导地位。所以取θ(MD)R=εθD,ε∈[0,1],本文取ε=1的情况。 本章中4种Model即集中决策模型、分散决策模型、制造商和分销商部分联盟模型和分销商和零售商部分联盟模型通过一阶条件得到均衡解,而后进行4种Model下的结果对比分析。 为了比较分析闭环供应链的绩效,首先考虑所有闭环供应链成员组成一个超组织集中决策者,制造商、分销商和零售商所有的交易行为是组织内部行为的情形[18],如图1所示。因此,Model C的闭环供应链利润函数可以表述为: (1) 通过一阶条件得到的决策,具有如下命题。 在分散模型中(如图1),因为制造商在闭环供应链中处于主导地位,所以无互惠偏好,而分销商对零售商具有互惠偏好,零售商也对分销商具有互惠偏好。分销商和零售商不仅关心自己的利润还关心对方的利润。分销商和零售商的效用函数如下: (2) (3) 其中0≤θD≤1和0≤θR<1分别是分销商和零售商的互惠偏好系数,系数越大,双方对于对方的利润关注程度就越大。 (4) (5) (6) 其中分销商和零售商的利润分别为πD=(wn-mn)qn+(wr-mr)qr和πR=(pn-wn)qn+(pr-wr)qr。 Model D也叫做非合作机制(Non-Cooperative Mechanism, NCM),作为第3章3种协调机制分析的基准情况。博弈结果采用逆向归纳法求解,以下命题为均衡决策的特征。 命题2在Model D中,博弈的均衡解可以表示为: 因此,最优销售量和利润分别为: 其中: 在这个模型中(如图1),制造商与分销商建立了一个两人联盟(MD),它们可以被看作一个集中决策者,决定着wn和wr。而后,零售商设定商品价格pn与pr。MD联盟会对零售商表现出互惠性,而此时的零售商则会对联盟MD表现出互惠性。因此,MD联盟的效用函数和零售商的效用函数如下所示: (7) (8) 两人联盟MD的目标和零售商一致,都是最大限度地提高自己的效用。联盟MD和零售商继续二级Stackelberg博弈。故Model MD的目标函数是由下式所确定: (9) (10) 命题3在Model MD中,博弈均衡解可以表示为: 因此最优的销量和利润分别为: 其中: 在这个模型中(如图1),分销商和零售商组成一个小联盟DR,在制造商的主导下,制造商与小联盟DR继续Stackelberg博弈。因此,Model DR的问题如下所示: (11) (12) 类似于Model C,若分销商和零售商组成联盟,则分销商的互惠偏好和零售商的互惠偏好将变得不重要。因此,制造商和联盟DR只有唯一目标,那就是最大化自身的利益。 博弈采用逆向归纳法求解,以下命题为均衡决策的特征。 在制造商为市场领导者的环境下,制造商处于竞争的优势地位,但零售商参与到合作的最低限度是能够从中获利,这一区间能使得零售商持续稳定地参与到合作之中。 命题5在区间Ω上有以下结论成立: 命题5表明集中决策下的渠道利润最高,而分散模型中利润最低。部分联盟的情况下渠道利润介于两者之间。这证明部分联盟方案可以提升闭环供应链的效率,只有当θD和θR在特定范围时,才能达到集中决策下的最佳利润水平。另外,在Model MD和Model DR中,互惠偏好会对渠道利润产生影响。这意味着,互惠偏好不仅影响着在不同成员间的利润分配,还影响着闭环供应链的效率。 本章中合作博弈将被用于解决三级闭环供应链成员之间剩余利润公平分配的问题。研究从个体理性和集体理性的角度来定义公平分配:公平分配方案必须提高每个成员的个体收益,并在集中的情况下获得最大化的渠道收益。 表2 互惠偏好下合作博弈的特征函数 表中: 定义1核心保障机制原则表明当三级闭环供应链成员组成集中决策时渠道利润达到最大合作K。在成员们愿意协调他们决定的前提下,本文的目的是为了找到一个稳定的分配方案,使得所有的成员都能更好地合作。令xM,xD和xR分别表示M,D,R的利润分配系数。一组(xM,xD,xR)只要满足以下两个条件,即可称作稳定: (1)个体理性xM≥v(M);xD≥v(D);xR≥v(R); (2)集体理性xM+xD+xR=v(SC)。 如果核是非空的,它的隐含分配方案使得大联盟保持稳定,即由于大联盟中所有成员都切实提高了收益,没有任何一个成员愿意离开大联盟,因此该方案使得大联盟得以稳定。接下来,将提出3种基于合作博弈理论的不同协调机制,每种协调机制都提出了独特的分配方案。 Shapley值[20]是合作博弈中被广泛接受的利润分配机制,如果这个参与者以完全随机的顺序进入所有可能的联盟,这就是每个参与者的平均边际贡献。基于合作博弈[G,v],G={M,D,R},每个闭环供应链成员的Shapley值可以被表示为: j=M,D,R。 (13) 现提出核仁解的概念,其目的是最小化分配方案的最大不满度[2,21]。将其应用于本文的合作博弈[G,v],按如下计算核仁解: minμ。 (14) s.t. (15) 其中:μ可被视为最不满意的局中人的不满,通过不断寻求有效解来最小化最不满意局中人的不满意度,再经线性规划的迭代求解以找到问题的核。值得注意的是,如果核仁确实存在,核仁总是处于核心。 若主要局中人希望鼓励供应链成员进行合作并组成大联合,则一种可能的机制就是通过适当分配利润来平衡他们的满意度。换言之,满意度被定义为分配利润和最小权利盈利之差与乌托邦盈利和最小权利盈利之差的比率[22]。其中,用Hi表示成员i的乌托邦盈利,它由文献[23]计算而来。用Li表示成员i的最小权利盈利。 Hi=v(MDR)-v(MDR/i), (16) (17) (18) (19) 在对Frisk等[25]的平等利润方法研究的基础上,本文提出一种新的利润分配机制,最大限度地减少最大满意度差异,称之为BSM。该协调机制给出了特征函数形式下[G,v]的合作博弈,BSM是一个线性规划: minf。 (20) (21) (22) (23) (24) (25) (26) 其中:约束(21)度量两个成员之间的两两满意度差异,允许目标函数最小化最大满意度差异;约束(22)和约束(23)确保最优分配处于核内;约束(24)和约束(25)保证了D的效用和R的效用在BSM下不会低于在分散决策下。因此,BSM分配方案的目标是平衡所有成员的满意度,同时确保个人的合理性、大联盟的稳定性,以及改善D和R的效用。 本章通过3种协调机制下的3个数值仿真实验和利润分配比较来研究在互惠偏好下三级闭环供应链的收入分配机制。本文给出一个数值仿真的例子,其中互惠偏好是固定的,分别为:θR=0.3,θD=0.6,并说明合作博弈在集中模型中分配渠道利润的应用。 根据第3章,在3个具有不同互惠偏好参数的协调机制下,有4个步骤获得独一无二的分配方案。本文给出一个数值仿真的例子,假设市场规模为1,且采用效用函数确定市场需求,设置互惠偏好是固定的,分别为:θD=0.6,θR=0.3,并说明了合作博弈在集中模型中分配渠道利润的应用。 (1)根据表2计算θD=0.6,θR=0.3时所有可能的联盟的特征值,相应的结果如表3所示。 (2)根据3.2节中核的概念和性质来检查博弈的核是否为空,为了更直观地观察到核在重心坐标中的位置,使用MATLAB中的TUGlab来计算3人博弈的核,将成图显示在图2中,阴影区域为θD=0.6,θR=0.3对应的核为非空。 表3 当θD=0.6,θR=0.3时的特征值 (3)在3种机制下的合作博弈解,表3中已经给出了特征值。 (4)检查得到的所有分配解是否在核中,特别是SVM求出的解。如图2所示,在重心坐标中,θD=0.6和θR=0.3时3种协调机制核的相对位置,从上往下依次为SVM,NSM,BSM。如图2所示所有分配解均在核内,这意味着所有解决方案均可以使大联盟稳定。 4.2.1 在三种协调机制下的利润分配比较 图3显示SVM和NCM下利润分配的比较,其中上层图为SVM的结果,下层图为NCM的结果。图3a~3c分别为制造商、分销商和零售商在两种情形下的比较。在NCM下,θD和θR都会影响M,D,R的利润,随着θD的增加,θR的减少,会使得M和R的利润增加,而D则与之相反,随着θD的增加,θR的减少,会降低D的利润。在SVM下,D和R都保持了与NCM相同的趋势,只有M,随着θD的增加,θR的减少,呈现出下降的趋势。更具体地说,图3a~图3c表明,在SVM下,D和M交替出现分配到的渠道利润的最大份额,然后是R,这不同于NCM的情况,因为在NCM下,由于制造商在供应链中起主导作用,所以M的份额最大。这一结果的原因是在SVM的分配原则下,基于3个成员加入不同联盟的平均边际贡献。给定的假设5,M和R组成一个联盟是不可能的,因为D在闭环供应链中有不可替代的作用,即v(MR)=0,这降低了M和R的边际贡献,但增加了D的边际贡献,在该假设下,D基本上取得了主导者的角色,因此,在总份额中跟M会呈现出交 替的趋势。此外,SVM是基于特征函数导出的,在SVM下的利润分配反映了特征函数的一般趋势。 图4显示NSM和NCM下利润分配的比较,其中上层图为NSM的结果,下层图为NCM的结果。图4a~4c分别为制造商,分销商和零售商在两种情形下的比较。无论在NCM还是NSM下,θD和θR都会影响M、D、R的利润。在NCM下,随着θD的增加θR的减少,M和R的利润都会增加,而D的利润反而会减少。在NSM下,D和R基本保持了和NCM一样的趋势,但是M会随着θD和θR的增加而增加。 如图5所示,在BSM下,M、D、R的趋势如NSM一样,基本保持了一致性,但M的趋势相对平缓。 图3和图4清楚地表明,相比于NCM,M,D,R在3种协调机制下具有更高的利润,其中M在SVM下会比较特殊,会先高于NCM,而后呈现出相反的趋势。总的来说,计算结果表明,SVM,NSM,ESM的约束能充分协调闭环供应链在集中决策的环境下达到最优的渠道收益。另外,数值仿真表明,3种协调机制下的分配方案都在核内,使得大联盟得以稳定。 这些数值研究证实上述3种协调机制可以在充分集中的情况下达到闭环供应链最佳的渠道利润。此外,图3和图4清楚地表明,由此产生的剩余利润分配方案可以提高每个闭环供应链成员的盈利能力。由于每个协调机制遵循鼓励合作的独特原则,不同闭环供应链 (Closed-Loop Supply Chain, CLSC)成员在这3种机制下的倾向有所不同。尽管如此,这进一步证明了这些分配方案在合作博弈的核内,使得大联盟稳定并为3位成员提供了可行的选择,以便彼此合作来实现个人和集体的改善。 4.2.2 D与R效用的比较 如图6所示为在3种协调机制与NCM之间进行零售商和分销商的效用比较。由图6a可以看出,D的效用在NCM下总是和θD、θR正相关。SVM、NSM、BSM的效用曲线高于NCM下的效用曲线,并且SVM下,D的效用是最高的。由图6b可以看出,R的效用在NCM下总是和θD、θR正相关。SVM、NSM、BSM的效用曲线高于NCM下的效用曲线,在θD和θR小于一定值时,NSM下的效用是最高的;反之,SVM下的效用会变为最高的。 基于M,D和R三层CLSC,本文考虑了D和R的互惠性的问题,并考虑了集中决策、分散决策和两个部分联合MD和DR模型4种情景。首先对这4种模型进行均衡分析,表明由于双重边际化,分散模式产生最高的价格、最低的再制品销售量、最高的新品销量和最低的渠道利润;两个部分联合模式产生相同的零售价格、销售量和渠道利润,其价值在分散和集中模式之间;在非合作模型中,互惠偏好导致D和与其相邻的下游决策者之间的利润分配也不同,互惠偏好导致R和与其相邻的上游决策者之间的利润分配也不同,同时还会影响闭环供应链的总利润。推导出合作博弈的特征函数后,提出了基于Shapley值、核仁解和平衡满意度3种协调机制,为闭环供应链成员提供利润分配方案。数值仿真证明,由此产生的剩余利润分配方案同时满足个人理性和集体理性,并落在合作博弈的核中,从而使大联盟得以稳定。比较分析D和R的互惠偏好系数如何影响闭环供应链成员的利润分配。尽管所有成员在3种协调机制下与分散模型相比能获得更高的利润,但数值仿真显示,D在SVM下获得利润的最高份额,M在NSM下获得最大利润,3名闭环供应链成员倾向于在BSM下获得更公平的利润。 未来可以在不同假设条件下的不同供给结构下开发合作模型,如具有3人互惠偏好的供应链合作博弈模型;合作博弈与供应链传统协调方式的比较等。2 闭环供应链非合作博弈模型及均衡分析
2.1 集中决策模型(Model C)

2.2 分散决策模型(Model D)
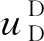
2.3 制造商和分销商合作模型(Model MD)

2.4 分销商和零售商合作模型(Model DR)

2.5 均衡结果对比分析
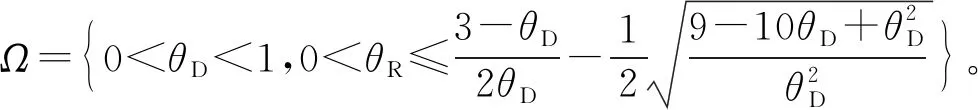

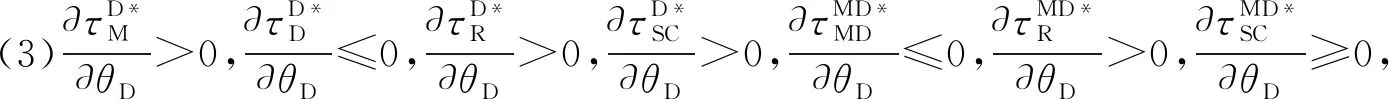



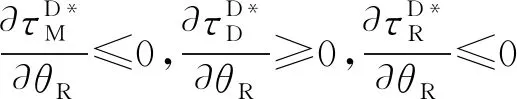
3 基于合作博弈的协调机制
3.1 合作博弈的特征函数
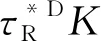

3.2 核心保障机制原则

3.3 Shapley值协调机制(SVM)

3.4 核仁解协调机制(NSM)
3.5 平衡满意度协调机制(BSM)


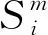
4 数值仿真与三种机制比较
4.1 三种协调机制下利润分配的解决过程

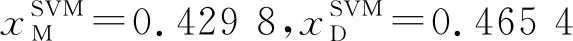
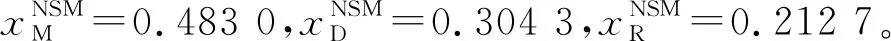

4.2 三种协调机制下的利润分配及D,R效用比较




5 结束语

