具有通用零部件的按订单装配系统库存位值平稳分布研究
金 鑫,王正肖,叶建芳,潘晓弘
(1.浙江大学 机械工程学院,浙江 杭州 310027;2.浙江大学 华南工业技术研究院,广东 广州 510700)
0 引言
按订单装配(Assemble to Order, ATO)生产系统的库存控制问题属于随机库存控制[1-3],从数学建模的角度来说,则属于随机离散线性规划[4-5]。DE KOK等[6]提供了一个对于ATO生产系统库存控制早期研究的全面综述(截止至2003年)。Zümbül等[7]则给出了ATO生产系统库存控制研究进度的一个简单整理。
由于ATO系统的复杂性,关于它的最优控制策略形式目前只有一些较简单的结论[8-11]。多数研究集中在给定的控制策略形式(包括库存补货策略和库存分配策略)下求解各种性能指标(如订单满足率、缺货队列分布、单位时间库存总成本等)的表达式,并进一步求解出控制策略中的最优参数[12-14]。
在ATO系统库存控制的研究中,库存水平、现有库存和库存位值是3个容易混淆的系统状态变量。其中,现有库存是指企业仓库中实际存放的每个零部件的库存数量,库存水平是现有库存与满足所有产品缺货所需的零部件数量之间的差值,库存位值是库存水平与在途库存的总和。可见,现有库存是直接产生库存持有成本的系统状态变量,而库存位值则是高层的、全局性的系统状态变量。常见的库存补货策略均是通过控制库存位值来间接控制现有库存(同时也会间接控制产品缺货),进而影响系统性能。如在(s,S)策略中,控制参数s与S均是库存位值,而在(r,nQ)策略中,再订货点r也是库存位值。
本文研究库存补货策略为(r,nQ)策略、产品需求到来和零部件补货提前期均随机的ATO系统。此时,系统任意时刻的库存位值是一个随机变量。若系统存在平稳状态,则其各种性能指标均与库存位值的平稳分布有关,因此研究库存位值的平稳分布是进行系统性能优化的第一步。在采用(r,nQ)策略的MTS系统中,一个经典的结论是:平稳时库存位值的分布是全空间(即r+1,r+2,…,r+Q)上的均匀分布(参见Sven[1]中的Proposition 5.1)。由于ATO系统结构的复杂性,使得(r,nQ)策略下ATO系统库存位值的平稳分布比按库存生产(Make to Stock, MTS)系统更为复杂。
ATO系统库存位值平稳分布的研究难点在于:①具有不同装配物料清单(Bill of Material,BOM)结构的ATO系统,其库存位值的分布空间结构也不同;②在一个典型的ATO系统中,有些零部件会用于多种产品的装配(即存在通用零部件),这些产品的需求会对通用零部件的库存位值产生叠加影响;③当库存位值的平稳分布存在不同的分布规律时,需要提供只基于结构参数的、简单有效的判定方法。由于上述难点,目前学界对ATO系统库存位值平稳分布的研究尚不成熟。其中,Song[15]首先证明了当库存位值的变化服从不可约、非周期的马尔可夫过程时,其平稳分布为全空间均匀分布。这一结论是对MTS系统库存位值平稳分布规律的研究成果的推广。然而,马尔可夫过程的不可约性不能直接从系统的BOM结构和库存补货策略中判断。Feng等[16]将该马尔可夫过程的不可约性的判定转化为对一系列线性同余方程组的有解性的判定,从而第一次提出了通过ATO系统的BOM结构和库存补货策略判定其库存位值的平稳分布的方法。
此后,学者们都假设库存位值的平稳分布为全空间上的均匀分布。如,Lu[17]用概率母函数法研究了产品需求服从更新过程、采取(r,nQ)策略的ATO系统,并研究了产品需求和补货提前期的波动性变化对系统性能的影响。Feng等[18]研究了(r,nQ)策略和先到先得(First Come First Served,FCFS)策略下的组装系统的产品期望缺货的表达式。但斌等[19]研究了采用准时制生产和(r,nQ)策略的混合补货策略的ATO系统,表明了企业对何种类型的零部件采用准时制生产补货方式能够降低供应链库存成本。Zhao[20]研究了(r,nQ)策略和FCFS策略下、零部件补货提前期为一般分布的ATO系统,得到了它的单位时间库存成本的表达式。而Reiman等[21]证明了虽然独立的(r,nQ)策略一般只是ATO系统的次优库存补货策略,然而其在效率上的损失被零部件的补货提前期的波动性所控制。当全空间均匀分布的假设不成立时,上述研究结论都需重新审视。
目前的研究尚有很多不充分之处,而一个完整的研究应包括如下方面:①确定库存位值的平稳分布规律的所有可能的情况;②针对库存位值不同分布规律情况的只基于结构参数的、简单有效的判定方法;③库存位值的不同分布规律对系统性能的影响。
本文将对上述3个问题给出一个初步的结论。针对第①个问题,证明了ATO系统库存位值的平稳分布只可能是全空间均匀分布或者是在某个子空间上均匀分布这两种情况,并证明了这些子空间之间是同构的;针对第②个问题,给出了一个全空间均匀分布的判定方法。与Feng等[16]不同,该方法本质上只需要求出一组线性同余方程组的解数即可,且还能求解出当平稳分布为子空间上均匀分布时,该子空间的状态个数;针对第③个问题,给出了库存分配策略为FCFS策略的情况下,使得单位时间库存总成本在各个子空间中都相等的充分条件,并通过近似表达式和仿真分析研究了在FCFS策略和先准备好先得(First Ready First Served,FRFS)策略下,当系统不满足该充分条件时,各子空间上的单位时间库存总成本的差异。
1 模型的基本概念、结构参数和基础假设
本节首先对ATO系统的一些重要概念给出简要的解释。
(1)物料清单(BOM) 是建造、制造或维修产品或服务所需的原材料、零部件和操作指南的详细列表。本文中涉及的BOM主要指产品的装配BOM。每种产品的装配BOM是指装配中需要用到的各零部件的数量,通常用向量表示。此时,整个系统的装配BOM可用矩阵表示。
(2)通用零部件 多种产品的装配都需要的零部件。
(3)库存补货策略 确定零部件何时补货、补货批量大小的库存控制策略。
(4)库存分配策略 确定产品需求何时满足、满足多少的库存控制策略。
(5)现有库存 企业仓库中实际存放的每个零部件的库存数量。
(6)在途库存 已经订货,但尚未到达目的地、正处于运输状态或等待运输状态的库存。
(7)产品缺货 已到来但未被满足的产品需求数量。
(8)库存水平 现有库存减去满足所有产品缺货所需的零部件数量即为库存水平。
(9)零部件缺货 库存水平取负后的绝对值为零部件缺货。
(10)库存位值 每个零部件的库存位值等于其库存水平加上其在途库存。
(11)平稳分布 一般而言,平稳分布是指随机过程中不受某些算子影响的特定的概率分布。特别的,马尔科夫过程的平稳分布是这样一类概率分布,若以它为初始分布,则该过程的有穷维分布是推移不变的。
(12)全空间 在(r,nQ)策略下,系统达到平稳状态时,库存位值的所有可能取值所组成的空间。
下面给出刻画ATO库存系统的结构参数。
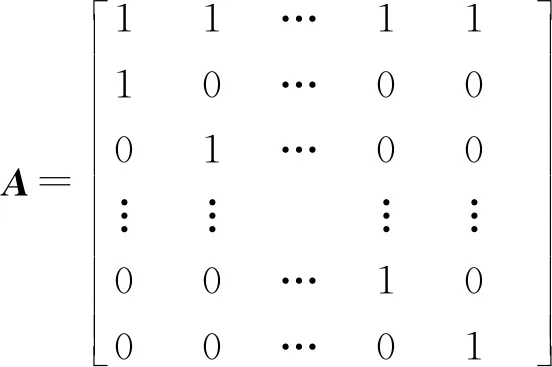
(1)BOM结构

(2)各项成本
在任何时刻,零部件i导致的库存持有成本与其现有库存成正比,产品j导致的缺货成本与其产品缺货成正比,零部件i的订货成本与其订货次数成正比。其中,零部件i的单个现有库存的单位时间库存持有成本为hi,产品j的单个缺货的单位时间缺货成本为bj,零部件i的单次订货成本为ui。
(3)零部件的补货提前期与产品的需求到来过程
当零部件i的补货提前期是确定值时,用Li表示,它们可以各不相同。当零部件i的补货提前期是一个随机变量时,用li表示,它们之间以及它们与系统状态之间相互独立。不同零部件的补货提前期可以服从不同的分布规律。不同产品的需求到来过程之间相互独立,产品的需求到来过程与系统状态之间相互独立。
(4)库存控制策略
ATO系统中的库存控制策略包括库存补货策略和库存分配策略。
在本文的研究中,假设采用(r,nQ)策略来管理零部件的库存补货。此时,零部件i相应的控制参数为ri和Qi。记

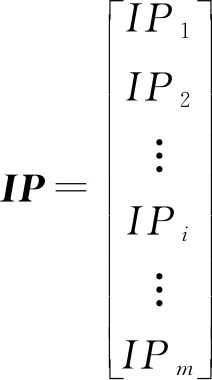
与本文研究有关的库存分配策略有FCFS策略和FRFS策略。FCFS策略将零部件的现有库存按产品需求到来的时间顺序进行分配,并且已分配的零部件库存无法被之后的产品需求使用。FRFS策略将零部件的现有库存按产品需求到来的时间顺序进行分配,并且如果某一产品需求无法被立即满足,则已分配给它的零部件库存可以被之后的产品需求使用。
2 ATO系统库存位值分布规律分析
本节主要分析ATO系统库存位值的分布规律。
引理1状态IP可到达状态IP′等价于∃x∈Nn,y∈Nm,使得IP-Ax+Θy=IP′。
证明由(r,nQ)策略的性质易知。
引理2若状态IP可到达状态IP′,则状态IP与状态IP′相通。
证明见附录。
定理1IP的整个状态空间被分成若干个(1个或多个)相互隔离的子空间,每个子空间内部的各状态是相通的。
证明由引理2易知。
引理3IP的任意两个子空间之间同构且子空间内各状态是对称的。
证明见附录。
引理4IP的边际分布(即第i个零部件的IPi分布,i=1,2,…,m)在任何一个子空间中都相同且都为均匀分布。
证明见附录。
定理2系统平稳时,IP的联合分布为在某个子空间上的均匀分布。(若只有一个子空间,则为全空间上的均匀分布)
证明因为在任一子空间上,所有状态相通,因此在该空间上的库存位值的马尔可夫链是有限、非周期、不可约的,所以存在唯一的平稳分布。又根据Song[15]可证明均匀分布为该情况下的一个平稳分布。综上所述,均匀分布为该情况下的唯一平稳分布。
例1考虑一个包含两种产品的ATO系统,其中:产品1由一个零部件1、一个零部件2和一个零部件3装配而成,产品2由一个零部件1和两个零部件2装配而成,Q1=Q2=3,Q3=2,r1=r2=r3=2。此时,经过简单计算就可看出库存位值的所有状态之间都是相通的。因此,系统平稳时,库存位值的联合分布为在全空间上的均匀分布。
例2考虑一个包含两种产品的ATO系统,其中:产品1由一个零部件1、一个零部件2和一个零部件3装配而成,产品2由一个零部件1和两个零部件2装配而成,Q1=Q2=Q3=3,r1=r2=r3=2。易知,库存位值的状态空间被分割成如下3个子空间:
子空间Ⅰ:[5,5,5]、[4,4,4]、[3,3,3]、[5,4,3]、[4,3,5]、[3,5,4]、[5,3,4]、[4,5,3]、[3,4,5];
子空间Ⅱ:[5,5,4]、[4,4,3]、[3,3,5]、[5,4,5]、[4,3,4]、[3,5,3]、[5,3,3]、[4,5,5]、[3,4,4];
子空间Ⅲ:[5,5,3]、[4,4,5]、[3,3,4]、[5,4,4]、[4,3,3]、[3,5,5]、[5,3,5]、[4,5,4]、[3,4,3]。
而且,所有状态的转化如图1所示。

图中:实箭头表示状态转化是被一个产品1的需求触发的,虚箭头表示状态转化是被一个产品2的需求触发的。
可见,在上述ATO系统中,子空间之间相互分离且同构,每个子空间内部各状态之间相通。因此,系统平稳时库存位值的联合分布为在某个子空间上的均匀分布(比如,若系统运行的初始状态为[4,3,3],则平稳时库存位值的联合分布为在子空间Ⅲ上的均匀分布)。
将上述结论与MTS库存系统对比之后可以看出:在MTS系统中,库存位值的分布为全空间上的均匀分布,而在ATO系统中,全空间上的均匀分布只是库存位值的联合分布可能出现的情况之一而已。显然,当库存位值的联合分布为全空间均匀分布时,系统各项性能指标的求解要比其为某个子空间上的均匀分布时更为简单,因此下一节将给出库存位值的联合分布为全空间均匀分布的判定方法。
3 全空间均匀分布的判定方法
本章将给出库存位值的联合分布为全空间均匀分布的充分必要条件。
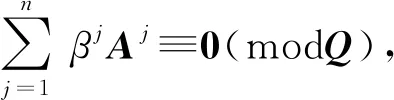
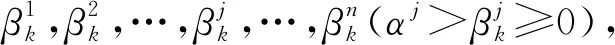
由于定理4是定理3的一个推广,因此,要证明这两个定理,只需证明定理4即可。
证明见附录。
由定理3和定理4可以求出任何一个ATO系统的库存位值的子空间个数。进而可以求出平稳时库存位值的联合分布情况。
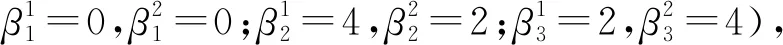
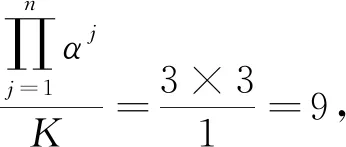
4 不同子空间中的库存位值分布对系统性能影响的比较研究
当平稳时库存位值的联合分布不为全空间上的均匀分布时,系统运行初始状态的不同将可能会导致库存位值平稳分布的子空间的不同,进而导致系统性能的不同。本章集中考虑在库存分配策略为FCFS策略和FRFS策略的情况下,库存位值在不同的子空间上分布会对系统库存总成本造成的影响。
为便于讨论,在以下分析中,均假设ATO系统的BOM矩阵是0-1矩阵,且产品j的需求到来过程是强度为λj的齐次泊松过程。下面的结论可以很自然地推广到任意BOM矩阵及复合齐次泊松过程的情况。
根据Zhao[21]和引理4,ATO系统在子空间V上的单位时间库存总成本有如下表达式:

当ATO系统采取FCFS策略时,某一产品的时段订单满足率只取决于装配它所需要的零部件的库存水平。因此,在FCFS策略下,对于某一产品,可以只考虑装配它的所有零部件的库存位值的分布规律,并将定理3、定理4限制到这些零部件上。若限制后的ATO系统满足判定条件,则该产品的时段订单满足率在各个子空间上均相同。由于产品的期望缺货E(B(s))被其时段订单满足率唯一确定,因此若针对所有产品限制后的ATO系统都满足判定条件,则它们的期望缺货在各个子空间上均相同。再由式(1)可知,所有子空间上系统的单位时间库存总成本cV(r,Q)均相同。
例5考虑一个两种产品的ATO系统,其中,产品1由一个零部件1和一个零部件2装配而成,产品2由一个零部件2和一个零部件3装配而成,Q1=Q3=Q2=2,r1=r2=r3=2。根据定理4可知该系统的状态空间被分成两个子空间,其中:
子空间Ⅰ:[4,4,4]、[3,3,4]、[3,4,3]、[4,3,3];
子空间Ⅱ:[4,4,3]、[3,3,3]、[3,4,4]、[4,3,4]。
虽然原ATO系统的状态空间被分成了两个相互独立的子空间,但是产品1和它的零部件、产品2和它的零部件各自组成的两个子系统却满足定理3或定理4。因此,该系统在FCFS策略下,产品1和产品2的期望缺货在子空间Ⅰ和子空间Ⅱ上是相同的,进而系统的单位时间库存总成本也是相同的。

例6考虑一个有两个产品的ATO系统。其中,产品1由一个零部件1、一个零部件2、一个零部件3和一个零部件4装配而成,产品2由一个零部件1和一个零部件2装配而成。Q1=Q2=Q3=Q4=2,r1=r2=r3=r4=0。根据定理4可知,库存位值的状态空间被分割成如下四个子空间:
子空间Ⅰ:[2,2,2,2]、[1,1,1,1]、[2,2,1,1]、[1,1,2,2];
子空间Ⅱ:[1,2,2,2]、[2,1,1,1]、[1,2,1,1]、[2,1,2,2];
子空间Ⅲ:[2,2,2,1]、[1,1,1,2]、[2,2,1,2]、[1,1,2,1];
子空间Ⅳ:[2,1,1,2]、[1,2,2,1]、[2,1,2,1]、[1,2,1,2]。
对于产品1,限制后的ATO系统不满足上述判定条件。
在FCFS策略和(r,nQ)策略下,目前并不存在能求解ATO系统的产品期望缺货的多项式时间复杂度的精确算法,因此,研究的重点集中在求出其近似表达式。其中,Lu等[23]通过将原系统“拆分”成若干分配系统,并用这些分配系统的单位时间库存总成本的和来作为原系统的单位时间库存总成本的近似。由引理3和引理4可知,“拆分”后的分配系统的单位时间库存总成本的和与子空间的选择无关,这也间接表明不同的子空间对ATO系统的单位时间库存总成本的影响是很小的。
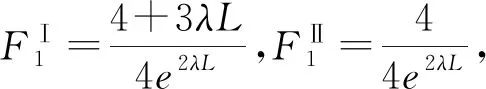

表1 例7中产品1的即时满足率随λL的变化规律

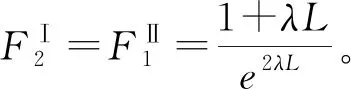
当ATO系统的库存分配策略采取FRFS策略时,某一产品的订单满足率不仅取决于装配它所需要的零部件的库存水平,还取决其他零部件的库存水平和现有库存,此时上述判定方法将会失效。下面通过一个简单的例子就可以看出这一点。
例8考虑例7中的ATO系统。

5 FCFS策略与FRFS策略下不同子空间中产品期望缺货的仿真实验
根据前面的证明过程,比较不同子空间对单位时间库存总成本的影响时,只需要考虑不同子空间对产品期望缺货的影响即可。设计仿真实验,研究FCFS策略和FRFS策略下不同子空间中的产品期望缺货的不同。这里以产品的期望缺货为目标,以零部件的到达间隔时间为变量进行仿真。
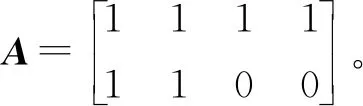

表2 仿真模型中零部件的相关参数

表3 仿真模型中产品的相关参数
当零部件C4初始库存位值为[2 2 2 2]时,该ATO系统平稳后的子空间为W1,初始库存位值为[2 2 2 1]时的子空间为W2。零部件C4的平均到达间隔时间的值为u。通过仿真实验,研究当u变化时,FCFS策略和FRFS策略下不同子空间中的产品期望缺货之间相对差距的变化。对于每一次实验,仿真总时间设定为70 000单位仿真钟时间。设定仿真钟时间前20 000为初始阶段,对20 000~70 000时间内的运行数据进行统计。零部件C4的平均到达间隔时间u在0.25~2之间每隔0.25取一个值。在每一次取值下,对FCFS策略和FRFS策略进行50次仿真。仿真结果如表4和表5所示。将表4和表5中FCFS策略和FRFS策略下不同子空间中的产品期望缺货的相对差距绘制折线图,如图3和图4所示。所有仿真中,p值均小于0.000 1。
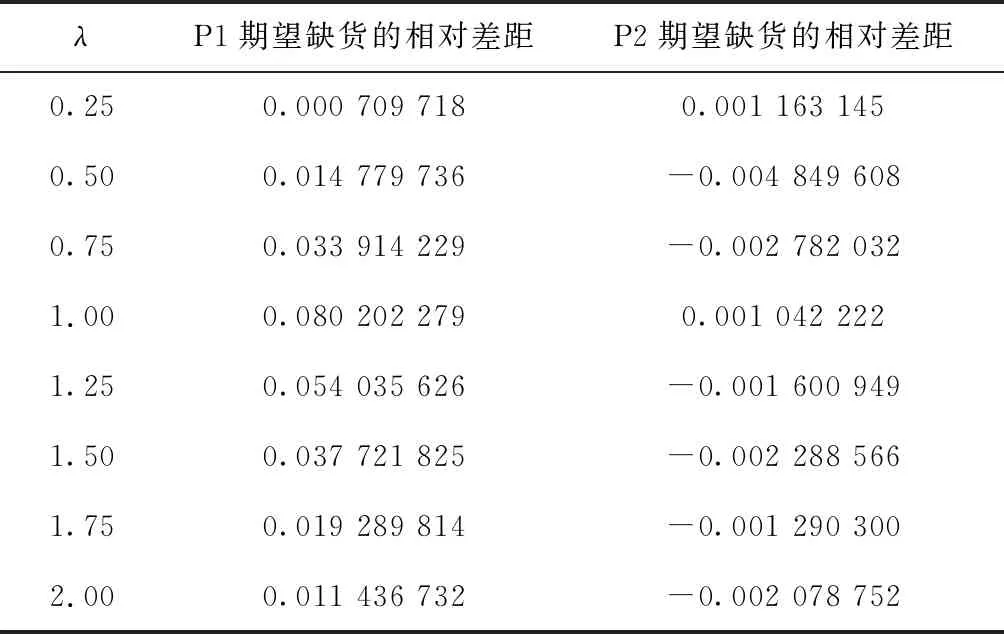
表4 FCFS策略下不同子空间中产品期望缺货相对差距

表5 FRFS策略下不同子空间中产品期望缺货相对差距

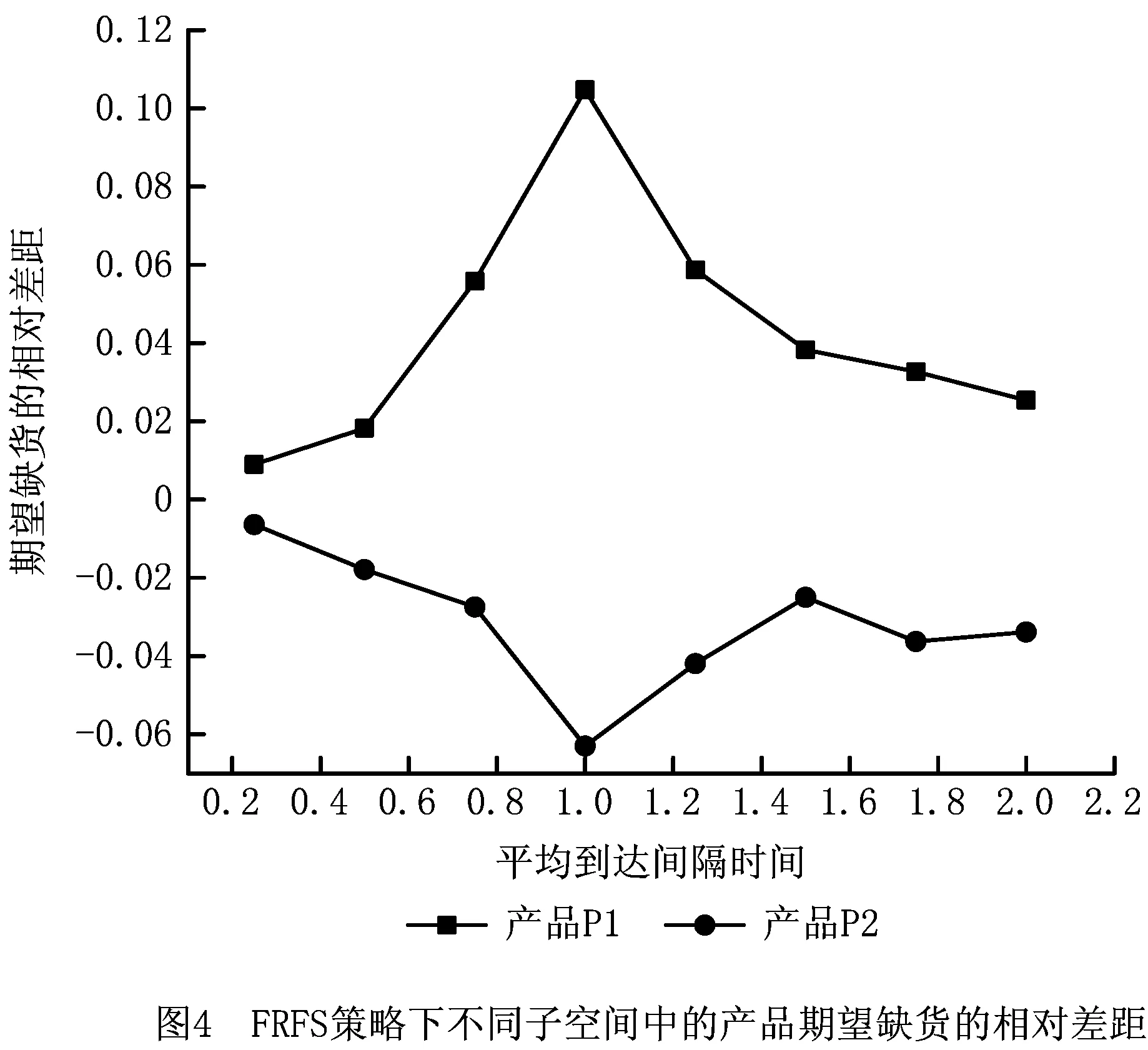
由图3和图4可以看出:
(1)FCFS策略下产品P1的期望缺货在不同子空间中差距较大,而产品P2的期望缺货在不同子空间中没有差别。FRFS策略下产品P1和产品P2的期望缺货在不同子空间中都有一定的差别。这一结果印证了第4节中关于FCFS策略与FRFS策略下不同产品在不同子空间中期望缺货差距的讨论。
(2)随着零部件C4的平均到达间隔时间的增大,FCFS策略下的产品P1以及FRFS策略下的产品P1、产品P2的期望缺货的相对差距均先增大后减小。换句话说,随着产品的期望缺货的增大,不同子空间下该产品的期望缺货的相对差距先增大后减小。该现象可以这样理解:当零部件C4的平均到达间隔时间很小时,子空间W1和子空间W2中产品的期望缺货主要取决于另外3种零部件,而这两个子空间限制到另外3种零部件上是相同的,因此产品的期望缺货相差不大。而当零部件C4的平均到达间隔时间很大时,子空间W1和子空间W2中产品的期望缺货主要取决于零部件C4,而这两个子空间限制到零部件C4上是相同的,因此产品的期望缺货相差也不大。
6 结束语
为了对一个ATO系统进行优化,需要知道在不同的库存策略下库存位值、库存水平、缺货、现有库存和在途库存等的分布规律。通常对库存系统分析是按照库存位值、在途库存、库存水平、缺货、现有库存的从易到难的路径进行的。然而,由于系统结构的复杂性,使得在(r,nQ)策略下ATO系统的库存位值的分布表现出一些MTS系统所不具有的性质。因此,需要首先对ATO系统平稳时的库存位值的分布规律进行分析。
本文沿着Song[15]的开创性工作,对ATO系统的库存位值分布规律做了更进一步的研究。主要包括以下内容:
(1)证明了平稳时ATO系统的库存位值的分布要么是在全空间上的均匀分布要么是在某个子空间(取决于运行初始状态)上均匀分布,并证明了子空间之间相互同构并且子空间内各状态对称。
(2)Feng等[16]曾给出了一个判定ATO系统的库存位值平稳分布是否是全空间均匀分布的方法,但该方法需要判定很多个线性同余方程组的解,因此较复杂。本文提供一个新的判定方法,该方法实质上只需要求出一个线性同余方程组的解的个数即可,且该方法还能求出每个子空间的状态的个数。
(3)最后通过近似表达式和仿真分析初步揭示了在FCFS策略和FRFS策略下,不同的ATO系统的库存位值分布规律对其系统性能的影响。
本文的研究表明,在很多情况下,ATO系统库存位值的平稳分布是在某个子空间上的均匀分布,不同子空间对于系统性能将会产生影响。由于初始值的不同将会导致库存位值在不同的子空间上分布,因此当企业在进行ATO系统的库存管理时,不仅需要确定库存控制策略的最优参数,还要确定系统运行的最优初始值。
在这一领域,还有很多工作需要完成,主要包括:
(1)建立一种更简单、更直接的判定ATO系统的库存位值平稳分布的方法。最好的结果是判定方法中无需求解方程组,而是可以通过BOM矩阵和补货矩阵直接求出平稳分布的规律,并通过求解能得到子空间内部更细致的性质。
(2)本文只在FCFS和FRFS策略下对不同子空间的ATO系统的单位时间库存总成本这一指标进行了分析,更进一步需要研究不同库存分配策略下不同子空间中的各种性能指标(如订单满足率、缺货队列分布、现有库存分布等)的表现差异随各参量的变化规律,最好能给出差值的近似上下限公式。

