基于逆线性二次型控制活套优化仿真设计
夏永彬 王海深 周广成 郭维进 李伟 路统宪
(北京首钢股份有限公司 河北唐山 064400)
1 前言
轧机间的活套在轧制中起着维持机架间秒流量平衡的作用,也保持带钢具有恒定张力的设定,然而活套的高度控制和张力控制两者存在耦合作用,当活套高度变化时,机架间张力会发生变化;机架间张力变化,角度也会发生变化,即活套控制是一个耦合系统[1-2]。机架间的套量由于在咬钢速降、稳态速度变化、带钢本体的干扰下,存在着一定的干扰,而张力由于轧制力的动态变化、轧机速度的干扰、带钢的问题,也会存在着一定的扰动控制。随着对带钢质量的要求增加,确保带钢间张力的稳定,对带钢质量的稳定具有十分重要的作用[3]。
2 ILQ控制理论与反馈极点配置
ILQ控制理论是LQ二次型理论的基础上逆向设计的,LQ设计流程图如图1所示。

图1 受控系统的控制模型
传统受控系统状态空间模型可以描述为:
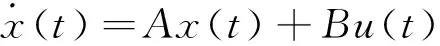
y(t)=Cx(t)
(1)
式中:x(t)—状态向量;
u(t)—控制向量;
A、B和C—常数矩阵;
y(t)—输出矩阵。
在上述系统中,设计最佳控制率u,实现上述系统的控制输出y渐进设定r,此时的反馈矩阵采用的矩阵为K,此时的J考虑到系统状态向量输出最低,控制率输出最小:
(2)
当最优控制存在且唯一,则
u=-Kx(t)=-R-1BTPx(t)
(3)
其中P是矩阵黎卡提代数方程的解
PA+ATP-PBR-1BTP+Q=0
(4)
进而可以通过黎卡提方程[K,P,E]=lqr(A,B,Q,R,N) 获得反馈控制率K。
其中黎卡提方程可以得出最优反馈控制K,设定的控制率u从而得出,采用该方式中Q和P加权矩阵往往需要大量经验实凑来获得[4-5]。这在实际调试中往往不具有应用条件,采用该方法进行Q和P的求解,往往只能应用到仿真理论设计中。
3 活套ILQ逆线性二次型理论对活套控制器参数的优化设计
3.1 活套的控制器模型参数
传统活套控器模型的优化,如下图2所示。
yA=CAxA
(5)
假设系统在稳态时:
(6)
上式中xs和us为稳态值,前者为状态向量,后者为控制率,得出活套模型控制器参数如下。
(7)

(8)
进而得出式子的控制率
(9)
通过上式中推到,可以得出在LQ基础上进行两级反馈的配置如图2所示。
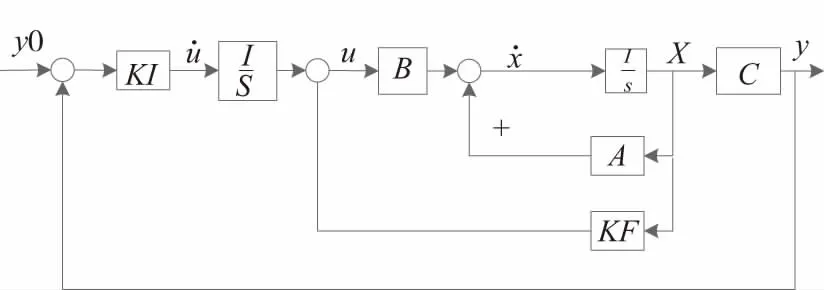
图2 活套新模型控制功能图
3.2 ILQ参数优化设计
3.2.1 逆线性二次型的反馈极点配置
新模型的反馈矩阵需要考虑两部分,包括反馈和积分增益。因此对上式所采用的ILQ理论进行期望极点配置,得到状态反馈矩阵中KF和KI.其中KF和KI两者之间具有一定线性关系,将[KFKI]进行线性变形,将该KI转换为单位矩阵组成的表达形式[6],如下式10所示。
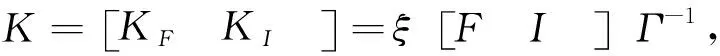
(10)
对于多输入多输出系统,极点配置所得到的反馈增益K往往不为一,上式表达出的反馈增益矩阵具有一定的可调节性。其中反馈增益KF求解可通过期望极点配置获得,过程如下。
其中F=-GT-1,G为特征向量自由度配置矩阵,T为自由配置矩阵,可以通过计算得出。
设计方法如下[7]:
(1)获取期望系统闭环极点{Si}。
(2)选择G=[g1g2…gn-m],其中G成为特征向量自由度配置矩阵。
当选择完G变量时,T=[t1t2…tn-m],其中ti=(siI-A)-1Bgi
(3)其中ξ应满足ξ≻λmax(E)(此处获取ξ的下限)
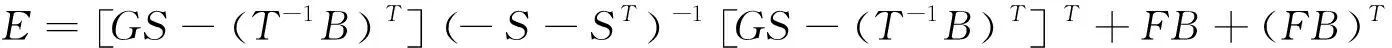
(4)构造上式,最终可以得到反馈矩阵K
当反馈矩阵K得出后,采用新控制器的活套模型响应特性将由闭环系统矩阵AA-BAK的特征值来决定,当ξ满足下限值时,那么通过线性变化,可以将特征方程线性描述为:
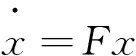
其中V是需要大于一定的下限值的值,∑为对角矩阵形式。
当ξ→∞,F的特征值λ(F)≈λ(A-BF)∪λ(-V-1∑V)
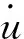
3.2.2 活套ILQ仿真与参数调节
对活套张力模型和高度模型进行建模[8],得出活套模型的状态矩阵方程:
上式中,E为带钢的杨氏模量(Mpa),J为转动惯量(Nms/rad);f为前滑系数,F1为角度对力矩的影响系数,F2为角速度对套量影响系数(m/rad),F3为张力对力矩的影响系数(Nm/Mpa),BT为液压缸流量增益系数,gl为角速度到角度转换系数。
通过闭环极点来推到反馈增益系数的过程:
A-BF=A-B(KFA+KIC)=(I-BKF)A-BKIC

假设闭环极点的位置期望和张力期望为wTC、wHC
则将行列式变成矩阵的形式,通过系数相同法可以得出相应的状态
采用多项式的系数相等法进行可以得出以下参数
通过上式描述可以得到系统的ILQ的控制框图,如图3所示。
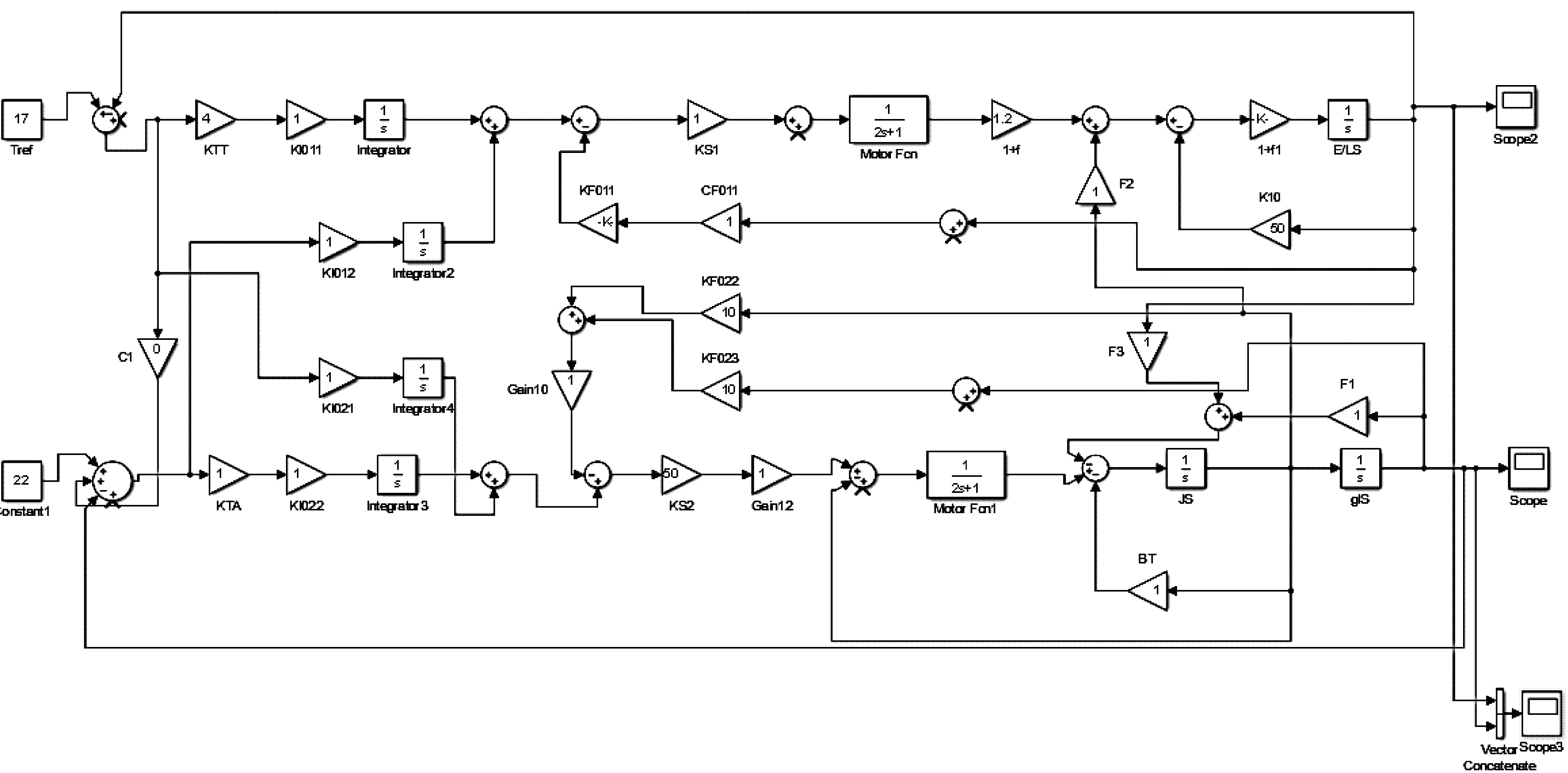
图3 活套新模型ILQ控制功能图
通过ILQ理论推导,活套模型是在LQ控制基础上改进模型而设计的,其中上式中的Ks1表示上式(10)中的单位设定参数,Ks2可调增益系数相当于式(10)中的增益系数ξ;设计反馈增益系数时,反馈增益系数KF和KI之间需满足一定线性关系;当ξ→∞,反馈增益的特征值将趋近于特征极点wHC、wTC,积分增益矩阵的特征值此时将趋近于无穷。
4 实际仿真参数设计
结合图3中的仿真设计,调节参数使得仿真输出图4(a)中在此基础上进行参数调节,设计张力输出17Mbar,角度设定输出为22°,与实际生产设定相符。
(1)图4(b)仿真设计中,当模型一定的时候,适当增加张力环可调增益系数Ks1,可以使张力响应增加,活套角度响应下降,调节该参数使得角度和张力响应过程趋势效果相反;

图4 单独增大参数Ks1
(2)图5(a)所示,适当增大Ks2=40,系统的角度响应速度和张力响应速度增加,具有良好的参数可调节性,该参数的调节区间范围较大。然而该参数不能太大,参数太大容易使得可投入的条件越来越苛刻,图5(b)中Ks2=80,响应初始阶段不具备条件。

图5 单独增大参数Ks2
(3)经过参数优化后,在扰动测试中,图6(a)中当对张力进行扰动时,角度会进行偏转以实现张力恢复到设定值,而在图6(b)中仅对角度进行扰动时,张力扰动变换具有较小干扰,这样会让在轧制中更加良好的保证带钢的质量。

图6 分别给张力和角度进行幅值干扰
5 应用效果
本次设计在结合着轧制屈服强度较大的难轧规格酸洗板Q420-P,在进行参数优化后,得到F6活套响应过程如图7所示:
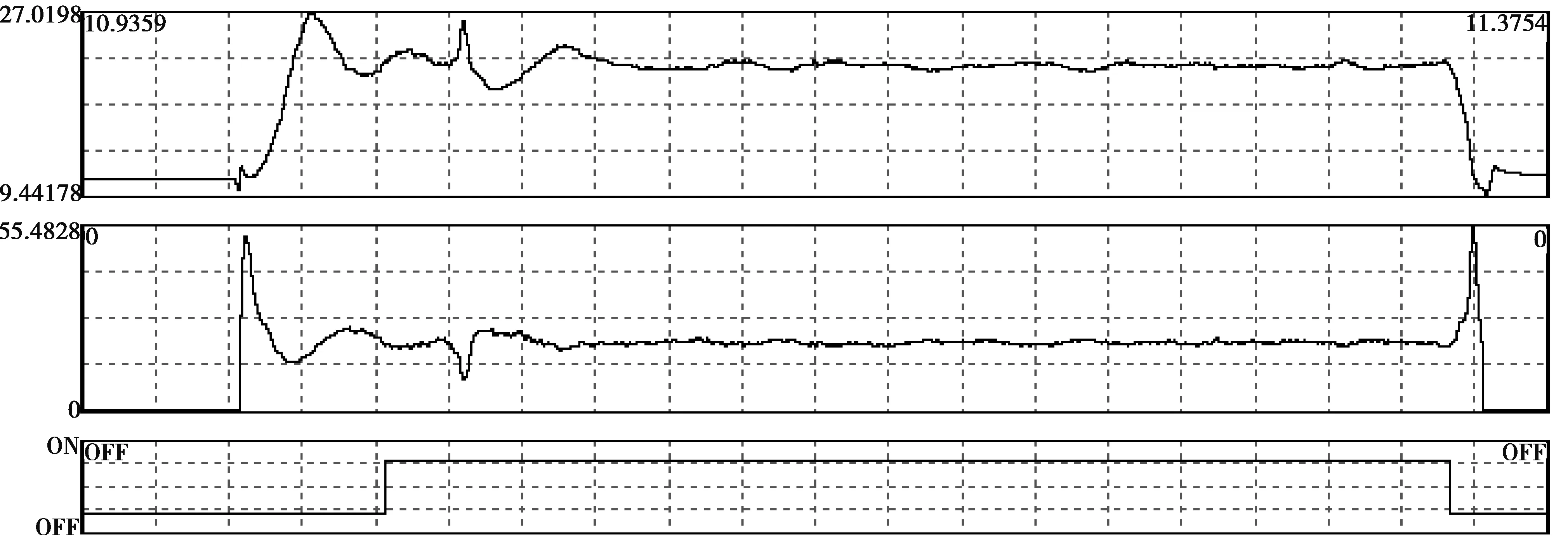
图7 投入ILQ设计的角度效果
在轧制过程,当角度在设定值稳定后程序自动切换成ILQ逆线性二次型控制中,在原参数基础,适当减小Ks1和增大Ks2参数,可以保证带钢在轧制中的稳定性。当张力出现扰动时,角度的变化明显,目的实现快速张力稳定,而角度扰动时,张力变化比较平稳,和理论仿真效果一致。
6 结论
本次设计在带钢建立张力到张力连轧阶段,提出了ILQ逆线性二次型优化控制设计,在活套进入张力连轧阶段,通过理论设计,适当调节参数ILQ逆线性二次型中的增益参数Ks1和Ks2,有效保持当出现张力扰动时,角度响应具有快速性,维持带钢张力稳定,当角度出现扰动时,张力具有一定的鲁棒性,保持带钢张力的稳定,仿真和实践都表明基于ILQ控制理论的活套控制效果良好,保证了生产的稳定性和质量的可靠性。

