基于改进的GPU并行NSGA-Ⅲ的土地利用优化配置

王海军，曾浩然，张文婷，张 彬，周玲慧

基于改进的GPU并行NSGA-Ⅲ的土地利用优化配置

王海军1,2，曾浩然1，张文婷3，张 彬1，周玲慧1

（1. 武汉大学资源与环境科学学院，武汉 430079；2. 武汉大学地理信息系统教育部重点实验室，武汉 430079；3. 华中农业大学资源与环境学院，武汉 430070）

土地利用优化配置是实现土地资源可持续利用的重要途径。该研究根据地理单元发展演变特点对基于参考点的非支配排序的遗传算法进行针对性改进，并耦合多目标优化方法，构建了土地利用空间优化模型。针对目前空间优化模型耗时过长，效率低的问题，该研究将GPU（Graphics Processing Unit, GPU）并行计算和土地利用优化配置模型有机结合，提升模型的优化效率。选取武汉市东西湖区进行实证研究，对比了模型在CPU（Central Processing Unit, CPU）串行计算和GPU并行计算2种方式下的运行耗时，并从最终优化结果中选取生态保护优先和经济发展优先2种典型方案进行分析。结果表明：1）GPU并行计算能够显著提升模型的优化效率，模型运行耗时由原来的158.08 h缩短到了1.68 h；2）模型能够统筹协调多个目标，对研究区域土地的数量结构和空间布局进行合理配置，为规划决策者提供多个可行方案。生态保护优先方案中，生态效益降低了6.16%，经济效益增长了13.64%；经济发展优先方案中，生态效益降低了6.19%，经济效益增长了15.86%。

土地利用；优化；非支配排序；遗传算法；GPU并行计算；武汉市东西湖区

0 引 言

21世纪以来，中国城镇化发展水平较快，常住人口城市化率从2000年的36.2%增加到2018年的59.58%[1]。随着城镇化的快速推进，建设用地急剧扩张，土地资源的供需矛盾日益突出[2]，阻碍了城镇化发展质量的提升。党的十八大和十九大报告也高度重视“生态文明建设”发展战略，强调区域的和谐发展、绿色发展。因此，积极探索并深入研究土地利用优化配置，协调有限的土地资源，保证区域的高质量发展具有重要现实意义。

土地利用优化配置是依据土地资源的自然属性和区域的社会经济状况，对区域土地资源的利用方式进行更加合理的数量安排和空间布局，遵循区位利用最佳、数量结构最优和综合效益最大的原则[3]。土地利用优化配置可以分为土地利用数量结构优化和空间布局优化2个方面[4]。国内外学者对土地利用数量结构优化研究开展了广泛且深入的研究[5-7]，研究结果对于政策和规划的制定具有较大的借鉴意义。但仅优化土地利用的数量结构，不考虑其空间布局，就无法将土地资源在空间上合理配置，释放其空间效应[8]。因此有学者在优化土地利用数量结构的基础上，采用CLUE-S（Conversion of Land Use and its Effects at Small region extent）[9]或元胞自动机模型[10]将优化后的土地利用数量结构配置到空间上，以逐步实现土地利用数量结构和空间布局的双优化。土地利用优化配置方案需要兼顾社会、经济和生态等多种效益，协调多方利益，是一种复杂的多目标空间优化问题[11]。随着GIS和计算机技术的发展，能够同步实现土地利用数量结构和空间布局双优化的智能算法逐渐成为研究热点，许多学者耦合智能算法和多目标优化模型[12-15]，同步优化了研究区域内土地利用的数量结构和空间布局。其中遗传算法由于其较强的全局寻优和空间搜索能力，常被用来解决土地利用多目标空间优化问题[16]。传统方法采用将多目标线性加权组合为单目标的方式进行优化搜索，效率高、求解能力强[17]，但在实际应用中，人为对多个目标进行赋权往往缺乏科学性。因此有学者提出了基于非支配排序的遗传算法（Nondominated Sorting Genetic Algorithm, NSGA）[18]，NSGA通过使用非支配排序方法，最终得出的是一个可供决策者选择的非支配解的解集，解集中每一个解的特点是：无法在改进任何目标的同时不削弱至少一个其他目标，这种方法在比较优化方案时，保留了各个目标的独立性，避免了权重设定带来的主观性。但使用非支配排序法时，排序的复杂程度为O(3)（为目标个数，为种群数量），算法对于大型种群规模的计算开销巨大[19]。继而有学者提出了NSGA-II，NSGA-II在一代的基础上进行改进，采用快速非支配排序方法降低了排序的复杂程度[19-20]。但当目标数多于3个时NSGA-II的优化效率会降低[21]，而土地利用优化所追求的目标涉及社会、经济、生态等多个方面[22-24]，3个目标通常过于局限。NSGA-III在目标空间引入参考点，利用与参考点间的联系紧密度筛选末级非支配等级个体，在NSGA-II降低排序复杂程度的基础上，提高了对于目标数量多于3个的多目标问题的优化效果[25]。为了在优化过程中体现不同土地利用类型之间的相互作用[26]并真实反应实际的空间变化情况，将随机区域重组算子和趋势变异算子替换了原始模型中的重组、变异算子，使模型与空间优化问题高度契合。

随着遥感技术的发展，高分辨率的遥感影像为进行更精细化的地理研究创造了条件，但也意味着研究时需要处理更大的数据集和进行更高强度的运算，进而对地理研究模型提出了更高的要求。目前，土地利用优化问题一般使用CPU进行计算，在处理多目标空间优化问题时耗时长、效率低，而将GPU并行计算应用于地理研究模型中，使每个地理单元都能并发、同步地参与计算，能够极大提高模型的计算效率[27]。目前，GPU并行计算已在图像处理[28]、统计学[29]、动力学[30]等众多研究领域得到了广泛的应用。本文结合改进的NSGA-III构建GPU并行的土地利用优化配置模型，并选择武汉市东西湖区为研究区域，进行实证研究。

1 研究区域与数据来源

1.1 研究区概况

东西湖区，隶属于湖北省武汉市，地处长江左岸，武汉市的西北部，汉江、汉北河及府环河汇合之处，介于30°34′－30°47′N，113°53′－114°30′E之间，境域东靠张公堤，分别与江岸区、江汉区和硚口区接壤；西南滨汉水与蔡甸区相望，西北依府河与黄陂区相邻，东西长38 km，南北宽22.5 km，总面积499.71 km2，2015年东西湖区土地利用现状如图1。东西湖区拥有大面积的水域和耕地，近年来，建设活动加剧导致大量农田和湖泊被侵占。为响应国家“生态文明建设”发展战略，《武汉市东西湖区土地利用总体规划（2006－2020）》中要求，东西湖区要通过对各类用地合理布局，形成农业、城镇建设、生态用地交融的土地发展格局。因此，合理配置区域土地尤为重要。

图1 2015年研究区土地利用现状图

1.2 数据来源

研究采用的土地利用数据为2015年武汉市东西湖区土地利用现状数据，分辨率为30 m×30 m，全区栅格总记955 090个，经ArcGIS重分类为耕地、建设用地、林地、草地和水域5类。模型中约束目标指标数据来源于《武汉市东西湖区土地利用总体规划（2006-2020）》《武汉市基本农田保护规划图》《武汉市绿地系统规划图》和《武汉市都市发展区范围线》。

2 研究方法

2.1 模型总体设计思路

模型总框架如图2，步骤可简要概括为：

第1步：将土地利用现状栅格数据转化为二维数组，并将数据传输到GPU中，利用GPU并行计算快速生成初始种群；

第2步：利用GPU计算出种群的多个目标值，获取种群个体的适宜度，通过选择、重组、变异获得子代种群；

第3步：计算子代种群的适宜度，合并父代和子代种群，并对合并后的种群进行非支配排序（12, …, F为非支配层级）、个体归一化和关联参考点操作。

第4步：修剪合并后的种群，并将其作为下一次迭代的父代种群，循环迭代直到达到预先设定的收敛条件，输出Pareto最优解集。

第五步：决策者从Pareto最优解集中选择适合的解，转化为土地利用优化配置方案。

图2 模型框架

2.2 GPU并行计算

随着硬件水平的不断提升，GPU已发展成为一种高度并行化的可编程处理器，具有极高的存储器带宽和杰出的计算效率[31-32]。研究使用CUDA作为GPU编程接口，将GPU并行计算应用到模型中，提高了模型的运行效率。

2.2.1 GPU并行计算原理

模型在进行优化的过程中，常需要对研究区域的所有地理单元进行遍历计算。常规的算法通常将数据集转化成二维矩阵后在CPU上进行计算，如图3a，需要依次逐个对地理单元进行计算。实际上，各个地理单元的计算过程是相对独立的，任何一个地理单元的计算对其他地理单元均不产生影响，整个过程是适合并行计算的，因此可以将计算过程交给GPU并行处理，如图3b，步骤如下：

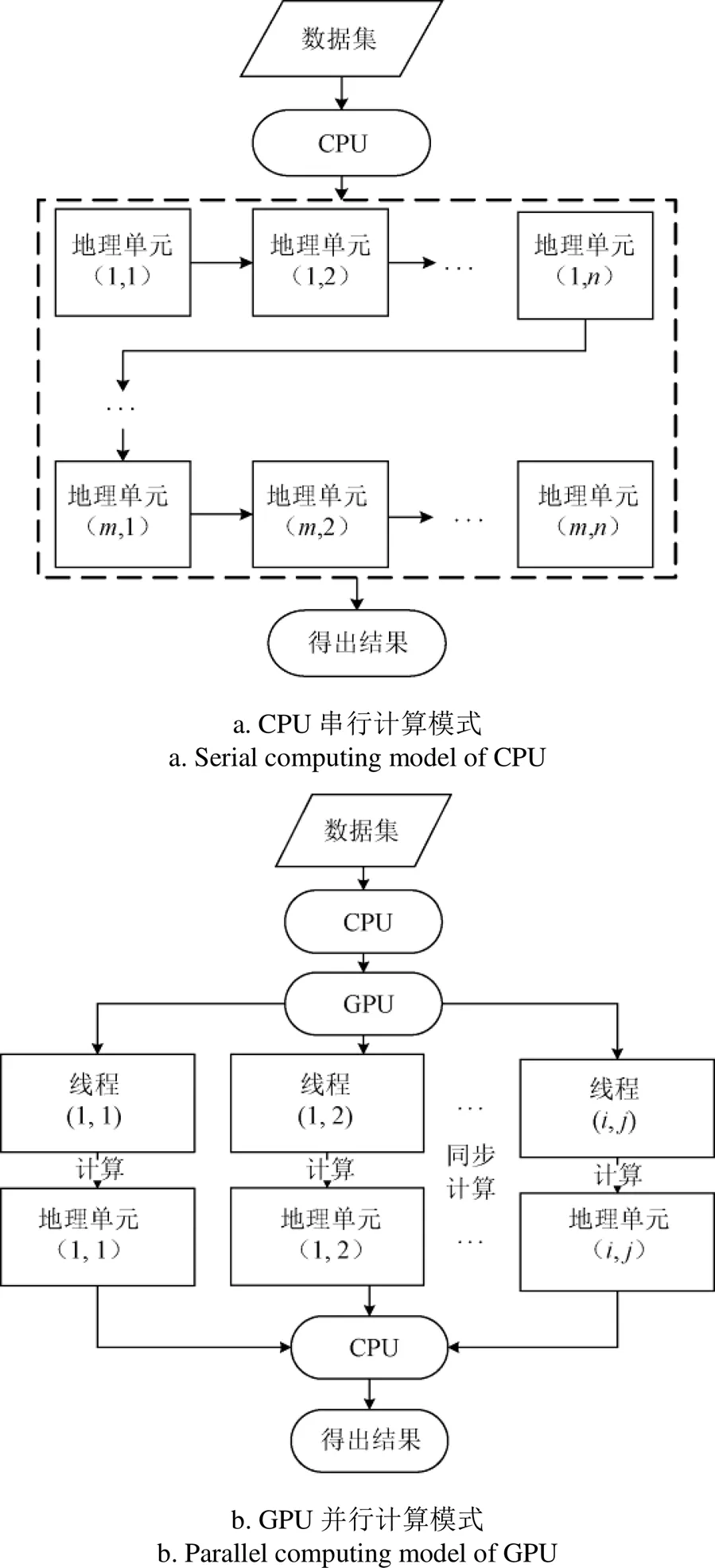
图3 CPU串行计算模式和GPU并行计算模式

第1步：空间数据集由CPU读取后传递到GPU。

第2步：设置CUDA并行架构：本模型中，Grid为二维结构，每个Block中包含16×16个Thread，Block的个数由下式确定：

（1）

其中Block表示Block的列数，Block表示Block的行数，Roundup表示向上取整，表示矩阵数据的列数，表示矩阵数据的行数。

第3步：将任务分配给各Thread，使每个Thread负责一个地理单元的计算。具体步骤：

①：获取当前Thread在Grid中的绝对位置坐标(start, start)；

②：获取现有架构中Grid包含的Thread的列数stride和行数stride；

③：坐标为(start, start)的Thread即负责坐标为(startstride, startstride) (,=0,1,2,3…)的地理单元的计算。

第4步：将计算完成的数据由GPU传递回CPU，得出计算结果。

将GPU并行计算应用到模型中时，需要根据不同的地理栅格数据集设置相应的CUDA并行架构，实现GPU利用率的最大化。

2.3 NSGA-III算子设置

2.3.1 选择算子

本研究采用锦标赛选择算子，即在种群中抽取个体，让它们进行竞争（锦标赛），抽取其中最优的个体进入下一代。此方法复杂度小且不易陷入局部最优，是遗传算法中最流行的选择策略。

2.3.2 随机区域重组算子

重组本质是模拟2个父代个体将部分基因调换，以生成新个体的操作。本文在传统重组算子的基础上进行改进：如图4a所示，随机创建整数1，2，1，2，其中1，2∈[0,)（为染色体矩阵的最大行数），1，2∈[0,)（为染色体矩阵的最大列数），则以(Min(1，2)，Min(1，2))和(Max(1，2)，Max(1，2))2点连线为对角线形成的矩形区域即为待重组染色体进行基因调换的空间区域。如此，以一个整体区域为单位进行重组运算，更能反映实际空间变化情况，避免传统遗传算法单点重组运算导致的子代和父代差异过大的问题。

2.3.3 趋势变异算子

变异是以很小的概率随机改变染色体的基因，以产生新的染色体，能够有效防止算法陷入局部最优。本文对传统遗传算法的变异算子进行改进：如图4b所示，借鉴混合蛙跳算法思路[11]，首先对变异区域进行用地冲突判断，若区域存在用地冲突，则待变异的空间单元将向邻域8个单元中占据数量优势的地类转变。趋势变异算子考虑了邻域效应对待变异地理单元的影响，降低了优化后空间破碎的概率。

2.4 土地利用优化配置多目标体系

结合武汉市东西湖区的实际发展的多个方面，本模型设计了4类目标，以实现区域土地利用经济、社会和生态等综合效益的最大化。

图4 重组算子和变异算子

2.4.1 经济效益目标

以最大化区域相对国内生产总值（Gross Domestic Product，GDP）为经济目标，通过专家打分和AHP层次分析法计算出各类土地利用类型对区域GDP贡献的相对大小[33]，以此作为经济效益目标的计算系数，计算公式如下：

式中M为区域经济效益；A为土地利用类型的经济效益贡献权重；x为区域土地利用类型的总面积，hm2；表示区域内有种土地利用类型。

2.4.2 生态效益目标

以最大化区域生态系统服务价值（Ecosystem Service Value，ESV）为生态效益目标，根据生态系统单位面积服务价值当量表[34]，计算公式如式下：

式中M为区域生态效益；B为土地利用类型的生态系统单位面积服务价值当量。

2.4.3 成本目标

将最小化土地利用转化成本作为目标，适当控制实施土地利用优化配置策略所耗费的经济成本。依据土地利用类型转换成本系数[14]，对比优化前后各个地块单元的土地利用类型变化，获取每个地块单元的转换成本系数，加和得到区域土地利用类型转换成本，计算公式如下：

式中M为区域土地利用类型转换成本；为整个研究区域；I为优化前位于(,)处的地块土地利用类型；C为其优化后的土地利用类型；f为基于土地利用类型转换成本系数矩阵的输入输出函数，即输入某地块优化前和优化后的土地利用类型，输出该地块的转换成本系数。

2.4.4 土地利用相容性目标

在土地利用系统中，特定的土地利用类型具有趋于集聚或对其周围土地利用类型有偏好的特性，这种趋势或偏好为土地利用相容性[35-36]。协调土地利用类型的空间分布能最大程度地减少相邻土地的利用冲突，增强区域可达性，降低资源消耗，使土地资源得到更高效的利用。依据土地利用类型不兼容性系数，计算地块与其×邻域范围内2−1个地块之间的不兼容值以得到每个地块的不兼容值，加和所有地块的不兼容值得到研究区域土地利用不兼容值，计算公式如下：

式中M为区域土地利用不兼容性值；为整个研究区域；A为区域内位置(,)处地块的土地利用类型；为该地块的邻域空间；B为中位置(,)处地块的土地利用类型；f为基于土地利用不兼容系数矩阵的输入输出函数，即输入中心地块和邻域内某地块的土地利用类型，输出二者间的不兼容值。

2.5 土地利用优化配置约束体系

2.5.1 数量结构约束

1）土地总面积约束

优化后，各土地利用类型面积总和等于研究区域总面积，即：

式中为研究区域总面积，hm2；x为第种用地类型的面积，hm2。

2）耕地面积约束

为保证区域粮食安全，落实耕地和基本农田保护政策，依据《武汉市东西湖区土地利用总体规划大纲（2006－2020年）》，设置优化后区域耕地面积1不低于17 329 hm2。

3）为了严格控制优化后建设用地总量，依据《武汉市东西湖区土地利用总体规划大纲（2006－2020年）》，设置优化后区域建设用地总面积2不超过13 615 hm2。

4）为了避免建设用地无序扩张，严格控制增量建设用地，依据《武汉市东西湖区土地利用总体规划大纲（2006－2020年）》，设置新增建设用地占用耕地面积1-2不超过1 595 hm2。

5）为了加强生态文明建设，依据《武汉市东西湖区土地利用总体规划大纲（2006－2020年）》，设置区域基础性生态用地占区域土地总面积的45%以上，即：

式中1为耕地面积，hm2；3为林地面积，hm2；4为草地面积，hm2；为研究区域总面积，hm2；为区域基础性生态用地覆盖率，=45%。

2.5.2 空间布局约束

1）基本农田保护区约束

根据《武汉市基本农田保护规划图》，对保护区域内的基本农田实施特殊保护，禁止保护区域内地块向其他地类转化。

2）绿地生态保护区约束

根据《武汉市绿地系统规划图》，对区域内的柏泉风景区、金银湖郊野公园以及高速路等道路的防护绿地实施特殊保护，限制区域内土地的开发。

3）城市发展边界约束

以《武汉市都市发展区范围线》作为参考，划定区域城市开发边界线，限制边界线外部区域的土地开发活动。

4）水域约束

将区域内水域设定为水体保护区，不可与其他地类之间转换。

3 结果与分析

3.1 GPU并行计算对模型加速效果分析

为了验证GPU并行计算对模型计算效率的提升效果，选择研究区不同分辨率的地理栅格数据，对常规算法和GPU并行算法在模型创建初始种群和迭代进化过程中的耗时进行对比。试验均在同一台电脑上进行，硬件条件为16GB内存，Inter(R)Core(TM)i7-8700处理器，NVIDIA GeForce GTX 1060 6GB显卡，Windows 10操作系统，采用python编程，使用Numba连接Python函数和CUDA。

从表1、2可以看出，在处理不同分辨率的数据时，GPU并行计算均能起到显著的加速效果。在创建种群过程，GPU并行计算较常规算法的加速比稳定在3.6倍左右，在种群进化迭代过程，GPU并行计算的加速比随着数据分辨率的增大而增大，在处理分辨率为120 m×120 m数据时，加速比为42.20倍，而处理分辨率为30 m×30 m的数据时，加速比达到了94.22倍，说明当数据分辨率越高时，GPU并行计算的加速效果越好。

表1 基于不同分辨率数据的常规算法和GPU并行算法创建种群耗时对比

表2 基于不同分辨率数据的常规算法和GPU并行算法每代进化耗时对比

将模型中的相关计算过程交由GPU并行计算完成，使创建种群过程的耗时由743.98 s减少到237.16 s，进化过程的总耗时由158.08 h减少到1.68 h，显著提升了土地利用优化配置模型的优化效率。

另一方面，数据分辨率越高，常规算法计算所需的时间就越久，这时，使用GPU并行算法的加速收益就更大，所以GPU并行算法在处理更大区域、更高分辨率空间数据时更具优势。

3.2 土地利用优化配置结果分析

利用模型对武汉市东西湖区进行土地利用空间优化配置，经过多次测试调整参数，最终设置种群大小为100，最大进化代数400，重组概率为0.8，变异概率为0.005。本模型采用非支配解的概念来筛选空间优化配置方案，优化过程中，搜索不断向着Pareto前沿方向前进，最终得到Pareto最优解集。进化过程中，种群的平均目标值变化情况如图5，随着进化的进行，土地相容性目标、成本目标和经济效益目标逐渐增加，生态效益目标逐渐降低，优化在接近400代时达到收敛。分别选取Pareto最优解集中生态效益最大的解和经济效益最大的解作为土地利用优化配置方案（以下简称方案1，方案2），优化后土地利用现状图分别如图6。优化前后各目标值的变化情况如表3，模型在尽量保证区域土地兼容性较高和优化成本较低的情况下，协调生态效益和经济效益2个目标，可以看出，2种方案都是牺牲了部分生态效益而提升了经济效益，使得区域综合效益得到显著提升。在方案1中，生态效益目标降低了6.16%，经济效益目标提高了13.64%；在方案2中，生态效益目标降低了6.19%，经济效益目标提高了15.86%。

图5 种群平均目标值变化图

图6 土地利用优化配置典型方案

表3 优化前后各目标值对比

进一步对优化配置的结果进行统计，2种方案的土地利用数量结构变化如表4。可以看出，2种方案在优化后，耕地、林地和草地数量均有所减少，建设用地的数量得到增加。这是由于东西湖区目前耕地占区域总面积的54.55%，占比较高，区域正处在发展阶段，为了提高区域的综合效益，整体的优化方向是在保证区域粮食安全的基础上，减少耕地数量，增加建设用地的数量。通过对优化前后土地利用结构进行分析，可以看出，方案1强调区域生态保护，耕地、林地和草地三类生态用地的减少数量均略微少于方案2；方案二强调区域经济发展，整个研究区建设用地的地理单元数量占比由原来的16.14%提高到了19.65%，提高了3.51%（19 268个），如图7，可以看出，在东部和南部区域，建设用地有明显的外延式发展，但由于区域西部有大范围的基本农田，并且部分处于城市发展边界之外，而北部有柏泉风景区，中东部有金银湖郊野公园，这些区域均为空间布局限制区域，政策的限制使得这些区域的发展明显受限。而也是由于在空间布局限制中增加了相关的绿地生态保护区限制，使得优化结果均处于考虑了生态保护的大情景下，导致了两种方案较为接近。根据《武汉市东西湖区土地利用总体规划（2006-2020）》，2种方案中，耕地数量和建设用地总规模均符合规划要求。

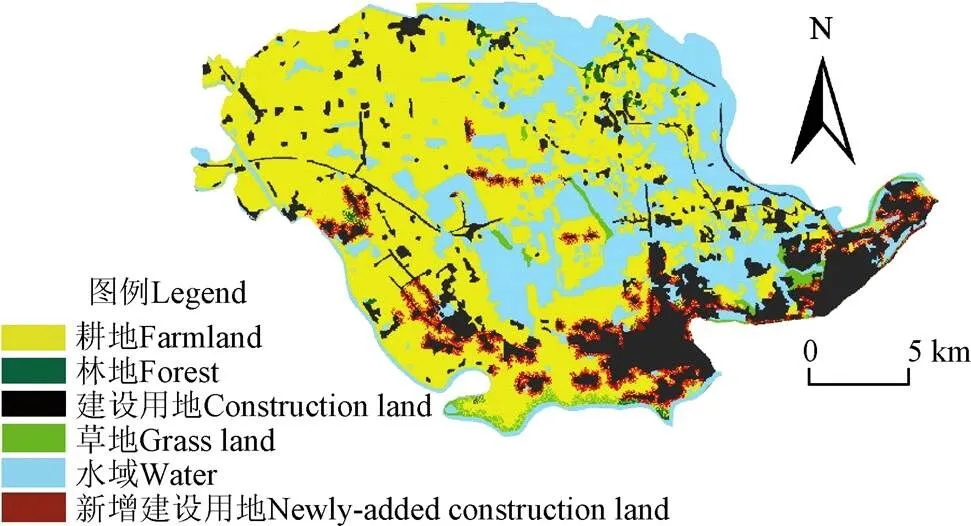
图7 方案2新增建设用地分布图

表4 优化前后土地的利用结构变化表

4 结论与讨论

本文采用NSGA-III构建多目标空间优化模型，目标函数包括经济效益目标、生态效益目标、成本目标和土地相容性目标4个子模型。同时改进了NSGA-III中的重组算子和变异算子，并辅以GPU并行运算，形成了基于GPU并行NSGA-III的土地利用优化配置模型，并选取武汉市东西湖区为例进行实证研究。

由于城市发展规划中，各目标的实现存在冲突，不可能存在使社会、经济、生态等目标都达到最优的解决方案，本研究构建的多目标空间优化模型最终得出的是一个Pareto最优解集，决策者可以根据需要从多个方案中选择适合的方案，具有较高的适用性。正处于发展中的区域可以选择经济效益目标较高的方案，优先发展经济；而处于经济发达的区域，可以选择生态效益较高的方案，加强生态保护。模型试验结果表明基于GPU并行NSGA-III的土地利用优化配置模型能够有效解决多目标空间优化问题，明显提高优化区域的经济、生态等综合效益，促进区域土地资源的可持续利用。将GPU并行计算应用到多目标空间优化模型中，使模型在面对庞大数据集和高强度计算时更具优势，能够极大提高土地利用空间优化配置效率。主要结论如下：

1）本文构建的土地利用优化配置模型对武汉市东西湖区在其现状的基础上进行优化，并选取结果中生态效益最大和经济效益最大的2个方案进行对比，结果均符合区域规划要求，在保证区域粮食安全，实施生态保护和避免建设用地无序扩张的前提下，提高了区域土地利用的综合效益。在未来的城市规划当中，涉及的目标是多样的，不仅限于本研究中的4个目标，模型中可以加入更多规划者所偏好的目标，帮助其解决现实的空间优化问题。

2）将模型中的相关计算过程交由GPU并行计算完成，使创建种群过程的耗时由743.98 s减少到237.16 s，进化过程的总耗时由158.08 h减少到1.68 h，显著提升了土地利用优化配置模型的优化效率。在地理研究偏向精细化的大数据时代，为进行更大区域空间优化、处理更高分辨率的地理空间数据创造了条件。

受数据及资料获取限制，未能将优化后的结果与研究区土地利用总体规划图进行对比，刻画规划和优化结果之间的相似区与冲突区。此外，模型仍存在一些局限性：1）模型采用GPU并行计算以提高计算效率，对于计算机的硬件要求较高，在没有GPU设备的计算机上运行时，模型效率较低；2）模型中的种群个数、重组概率和变异概率等参数需要经过多次试验测试后确定，未实现参数调整的自动化。后续研究将进一步细化相关政策规划数据，探索自动化调参机制，增强模型的稳定性与适用性。

[1] 杜霞，孟彦如，方创琳，等. 山东半岛城市群城镇化与生态环境耦合协调发展时空格局[J/OL]. 生态学报，2020，40(16)：5546-5559.

Du Xia, Meng Yanru, Fang Chuanglin, et al. Spatio-temporal characteristics of coupling coordination development between urbanization and eco-environment in Shandong Peninsula urban agglomeration[J/OL]. Acta Ecologica Sinica, 2020, 40(16): 5546-5559. (in Chinese with English abstract)

[2] 刘彦随，郑伟元. 中国土地可持续利用论[M]. 北京：科学出版社，2008.

[3] 刘彦随，蒋建军，李九全. 论城市土地优化配置的原则及标准[J]. 南京师大学报：自然科学版，1996，19(3)：73-77.

Liu Yansui, Jiang Jianjun, Li Jiuquan. Study on the principles and standards of optimal disposition in urban land[J]. Journal of Nanjing Normal University: Natural Science, 1996, 19(3): 73-77. (in Chinese with English abstract)

[4] 魏伟，颉耀文，魏晓旭，等. 基于CLUE-S模型和生态安全格局的石羊河流域土地利用优化配置[J]. 武汉大学学报：信息科学版，2017，42(9)：1306-1315.

Wei Wei, Xie Yaowen, Wei Xiaoxu, et al. Land use optimization based on CLUE-S model and ecological security scenario in Shiyang river basin[J]. Geomatics and Information Science of Wuhan University, 2017, 42(9): 1306-1315. (in Chinese with English abstract)

[5] 李鑫，欧名豪，刘建生，等. 基于不确定性理论的区域土地利用结构优化[J]. 农业工程学报，2014，30(4)：176-184.

Li Xin, Ou Minghao, Liu Jiansheng, et al. Regional land use structure optimization under uncertain theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(3): 176-184. (in Chinese with English abstract)

[6] 刘艳芳，李兴林，龚红波. 基于遗传算法的土地利用结构优化研究[J]. 武汉大学学报：信息科学版，2005(4)：288-292.

Liu Yanfang, Li Xinglin, Gong Hongbo. Optimization for land use structure based on genetic algorithms[J]. Geomatics and Information Science of Wuhan University, 2005(4): 288-292. (in Chinese with English abstract)

[7] Campbell J C, Radke J, Gless J T, et al. An application of linear programming and geographic information systems: cropland allocation in antigua[J]. Environment and Planning A-Economy and Space, 1992, 24(4): 535-549.

[8] 许小亮，李鑫，肖长江，等. 基于CLUE-S模型的不同情景下区域土地利用布局优化[J]. 生态学报，2016，36(17)：5401-5410.

Xu Xiaoliang, Li Xin, Xiao Changjiang, et al. Land use layout optimization under different scenarios by using the CLUE-S model[J]. Acta Ecologica Sinica, 2016, 36(17): 5401-5410. (in Chinese with English abstract)

[9] Zhang Wenting, Wang Haijun, Cao Kai, et al. Ecological conservation- and economic development-based multiobjective land-use optimization: Case study of a rapidly developing city in central China[J]. Journal of Urban Planning and Development, 2019, 145(1): 05018023.1－05018023.12.

[10] 刘菁华，李伟峰，周伟奇，等. 权衡城市扩张、耕地保护与生态效益的京津冀城市群土地利用优化配置情景分析[J]. 生态学报，2018，38(12)：4341-4350.

Liu Jinghua, Li Weifeng, Zhou Weiqi, et al. Scenario simulation balancing multiple objectives for optimal land use allocation of the Beijing-Tianjin-Hebei megaregion[J]. Acta Ecologica Sinica, 2018, 38(12): 4341-4350. (in Chinese with English abstract)

[11] 袁满，刘耀林.基于多智能体遗传算法的土地利用优化配置[J]. 农业工程学报，2014，30(1)：191-199.

Yuan Man, Liu Yaolin. Land use optimization allocation based on multi-agent genetic Algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(1): 191-199. (in Chinese with English abstract)

[12] 郭小燕，刘学录，王联国. 基于混合蛙跳算法的土地利用格局优化[J]. 农业工程学报，2015，31(24)：281-288.

Guo Xiaoyan, Liu Xuelu, Wang Lianguo. Land use pattern optimization based on shuffled frog leaping algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(24): 281-288. (in Chinese with English abstract)

[13] 莫致良，杜震洪，张丰，等. 基于可扩展多目标蚁群算法的土地利用优化配置[J]. 浙江大学学报：理学版，2017，44(6)：649-659，674.

Mo Zhiliang, Du Zhenhong, Zhang Feng, et al. Landuse optimizing allocation based on extensible multi-objective ant colony algorithm[J]. Journal of Zhejiang University: Science Edition, 2017, 44(6): 649-659, 674. (in Chinese with English abstract)

[14] Zhang Wenting, Wang Haijun, Han Fengxiang, et al. Modeling urban growth by the use of a multiobjective optimization approach: Environmental and economic issues for the Yangtze watershed, China[J]. Environmental Science & Pollution Research, 2014, 21(22): 13027-13042.

[15] 马世发，何建华，俞艳. 基于粒子群算法的城镇土地利用空间优化模型[J]. 农业工程学报，2010，26(9)：321-326.

Ma Shifa, He Jianhua, Yu Yan. Model of urban land-use spatial optimization based on particle swarm optimization algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(9): 321-326. (in Chinese with English abstract)

[16] 张骏杰，高延利，蔡玉梅，等. 基于“多规合一”的市级国土空间优化方法：以烟台市为例[J]. 地理科学进展，2018，37(8)：1045-1054.

Zhang Junjie, Gao Yanli, Cai Yumei, et al. Spatial optimization on the municipal level based on “multiple planning integration”: A case study of Yantai City[J]. Progress in Geography, 2018, 37(8): 1045-1054. (in Chinese with English abstract)

[17] Foroughi S, Hamidi J K, Monjezi M, et al. The integrated optimization of underground stope layout designing and production scheduling incorporating a non-dominated sorting genetic algorithm (NSGA-II)[J]. Resources Policy, 2019: 63, 101408.

[18] Srinivas N, Deb K. Multiobjective optimization using nondominated sorting in genetic algorithms[J]. Evolutionary Computation, 1994, 2(3): 221-248.

[19] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[20] Han Huaizhi, Yu Ruitian, Li Binxi, et al. Multi-objective optimization of corrugated tube inserted with multi-channel twisted tape using RSM and NSGA-II[J]. Applied Thermal Engineering, 2019, 159, 113731.

[21] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach,part I: Solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601.

[22] 王蓓，赵军，胡秀芳. 石羊河流域生态系统服务权衡与协同关系研究[J]. 生态学报，2018，38(21)：7582-7595.

Wang Bei, Zhao Jun, Hu Xiufang. Analysison trade-offs and synergistic relationships among multiple ecosystem services in the Shiyang River Basin[J]. Acta Ecologica Sinica, 2018, 38(21): 7582-7595. (in Chinese with English abstract)

[23] 宋戈，王越，刘馨蕊. 松嫩高平原土地利用格局优化模式建构研究[J]. 经济地理，2019，39(9)：191-197.

Song Ge, Wang Yue, Liu Xinrui. Optimization model of land use pattern in high altitude area of songnen plain[J]. Economic Geography, 2019, 39(9): 191-197. (in Chinese with English abstract)

[24] 马冰滢，黄姣，李双成. 基于生态-经济权衡的京津冀城市群土地利用优化配置[J]. 地理科学进展，2019，38(1)：28-39.

Ma Bingying, Huang Jiao, Li Shuangcheng. Optimal allocation of land use types in the Beijing-Tianjin-Hebei urban agglomeration based on ecological and economic benefits trade-offs[J]. Progress in Geography, 2019, 38(1): 28-39. (in Chinese with English abstract)

[25] 高云凯，马超，刘哲，等. 基于NSGA-III的白车身焊装生产平台的离散拓扑优化[J/OL]. 上海交通大学学报：1-19. [2020-11-16]. https://doi.org/10.16183/j.cnki.jsjtu.2020.99.001.

Gao Yunkai, Ma Chao, Liu Zhe, et al. Discrete topology optimization of body-in-white welding production platform based on NSGA-III[J/OL]. Journal of Shanghai Jiaotong University,1-19.[2020-11-16].https://doi.org/10.16183/j.cnki.jsjtu.2020.99.001. (in Chinese with English abstract)

[26] Hagoort M, Geertman S, Ottens H. Spatial externalities, neighbourhood rules and CA land-use modelling[J]. Annals of Regional Science, 2008, 42(1): 39-56.

[27] Guan Qingfeng, Shi Xuan, Huang Miaoqing, et al. A hybrid parallel cellular automata model for urban growth simulation over GPU/CPU heterogeneous architectures[J]. International Journal of Geographical Information Science, 2016, 30(3): 494-514.

[28] 李朝奎，方军，肖克炎，等. 基于GPU的地形可视化加速算法研究[J]. 地球学报，2020，41(2)：303-308.

Li Chaokui, Fang Jun, Xiao Keyan, et al. Research on acceleration algorithm of terrain visualization based on GPU[J]. Acta Geoscientica Sinica, 2020, 41(2): 303-308. (in Chinese with English abstract)

[29] 逯志宇，王建辉，王大鸣，等. 基于GPU的并行遗传算法在时频差估计中的应用[J]. 信息工程大学学报，2015，16(5)：552-556.

Dai Zhiyu, Wang Jianhui, Wang Daming, et al. Application of GPU-based parallel genetic algorithm in TDOA and FDOA[J]. Journal of Information Engineering University, 2015, 16(5): 552-556. (in Chinese with English abstract)

[30] Nandal P, Sharma R P. Numerical simulation on GPUs with CUDA to study nonlinear dynamics of whistler wave and its turbulent spectrum in radiation belts[J]. Computer Physics Communications, 2020, 254.

[31] 熊超. 基于GPU的连续波雷达频谱分析与谱峰搜索技术研究[D]. 长沙：国防科学技术大学，2011.

Xiong Chao. Research on Spectral Analysis and Peak Search of Continuous Wave Radar Based on GPU Hardware[D]. Changsha: National University of Defense Technology, 2011. (in Chinese with English abstract)

[32] 李秀滢，吉晨昊，段晓毅，等. GPU上SM4算法并行实现[J]. 信息网络安全，2020，20(6)：36-43.

Li Xiuying, Ji Chenghao, Duan Xiaoyi, et al. Parallel implementation of SM4 algorithm on GPU[J]. Netinfo Security, 2020, 20(6): 36-43. (in Chinese with English abstract)

[33] 龚建周，刘彦随，张灵. 广州市土地利用结构优化配置及其潜力[J]. 地理学报，2010，65(11)：1391-1400.

Gong Jianzhou, Liu Yansui, Zhang Ling. The optimal allocation of land use and its potential appraisal in Guangzhou City[J]. Acta Geographica Sinica, 2010, 65(11): 1391-1400. (in Chinese with English abstract)

[34] 谢高地，甄霖，鲁春霞，等.一个基于专家知识的生态系统服务价值化方法[J]. 自然资源学报，2008，23(5)：911-919.

Xie Gaodi, Zhen Lin, Lu Chunxia, et al. Expert knowledge based valuation method of ecosystem services in China[J]. Journal of Natural Resources, 2008, 23(5): 911-919. (in Chinese with English abstract)

[35] Cao Kai, Huang Bo, Wang Shaowen, et al. Sustainable land use optimization using boundary-based fast genetic algorithm[J]. Computers Environment & Urban Systems, 2012, 36(3): 257-269.

[36] Ligmann-Zielinska A, Church R L, Jankowski P. Spatial optimization as a generative technique for sustainable multiobjective land-use allocation[J]. International Journal of Geographical Information Science, 2008, 22(6): 601-622.

Land use optimization allocation based on improved NSGA-Ⅲ by GPU parallel computing

Wang Haijun1,2, Zeng Haoran1, Zhang Wenting3, Zhang Bin1, Zhou Linghui1

(1.,,430079,; 2.,430079,; 3.,430070)

The contradiction between supply and demand of land resources has become increasingly prominent, as the rapid development of urbanization. This problem has hindered the improvement of urbanization and development quality. The optimization of land-use allocation can bean important approach to coordinate the limited land resources, and thereby to ensure the high-quality development of a city. This study aims to establish a spatial optimization model of land use via a multi-objective optimization model with NSGA-III. A multi-objective model consists of the main and the constraint objectives. The main objectives include the maximization of GDP value, the maximization of ESV, the minimization of changing cost from the status que, and the minimized incompatibility of land use types. Besides, the constraint objectives are comprised of 5 quantitative constraints and 4 spatial constraints dataset according to policy planning. The NSGA-III can be well used to solve the multi-objective space optimization of land use, due to its excellent ability of global optimization and spatial search. The recombination and mutation operator were improved, based specifically on the characteristics and developments of geographical units. The efficiency of modified model was improved remarkably via integrating the GPU parallel computing. The Dongxihu District of Wuhan, China, was taken as the study area to test the model. Two typical schemes, including ecological and economic priority, were analyzed to compare the time-consuming of model in the serial computing of CPU and parallel computing of GPU. Consequently, the results demonstrated that: 1) A better optimization efficiency of modified model can be obtained using the GPU parallel computing, where the computing time reduced from 158.08 hours to 1.68 hours. 2) The modified model can be used to coordinate multiple objectives, and thereby to reasonably optimizing land use in terms of quantity structure and spatial pattern, providing for the multiple selections indecision making. In the scheme of ecological priority, the ecological benefits of study area reduced by 6.16%, and the economic benefits increased by 13.64%. In the scheme of economic priority, the ecological benefits reduced by 6.19%, and the economic benefits increased by 15.86%.

land use; optimization; non-dominated sorting; genetic algorithm; GPU parallel computing; Dongxihu District of Wuhan

王海军，曾浩然，张文婷，等. 基于改进的GPU并行NSGA-Ⅲ的土地利用优化配置[J]. 农业工程学报，2020，36(21)：283-291. doi：10.11975/j.issn.1002-6819.2020.21.034 http://www.tcsae.org

Wang Haijun, Zeng Haoran, Zhang Wenting, et al. Land use optimization allocation based on improved NSGA-Ⅲ by GPU parallel computing[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(21): 283-291. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.21.034 http://www.tcsae.org

2020-08-07

2020-09-25

国家自然科学基金项目（41601415）。

王海军，博士，教授，主要从事地理模拟、城市规划和土地资源评价研究。Email：landgiswhj@163.com

10.11975/j.issn.1002-6819.2020.21.034

F301.2

A

1002-6819(2020)-21-0283-09