考虑流固耦合的厚壁输水管水锤和振动特性分析

郭 强，周建旭，黄 亚，张 健

考虑流固耦合的厚壁输水管水锤和振动特性分析

郭 强，周建旭※，黄 亚，张 健

（河海大学水利水电工程学院，南京 210024）

厚壁管对瞬变流具有很高的抗风险能力，在输水系统中得到了广泛的应用。为了研究厚壁管中流固耦合现象，该研究考虑轴向应力的缓冲效应，基于薄壁管流固耦合分析模型（薄壁模型），建立并提出了适用于厚壁管流固耦合一维模型（厚壁模型）。采用有限体积法对模型求解，压力振荡数值结果与已有的试验结果峰值相对误差低于4.5%，说明厚壁模型是可靠的。在此基础上，从压力振荡、波速及管道振动角度比较了2模型差异：薄壁模型和厚壁模型模拟波速与试验结果相对误差分别为4.6%和1.3%；相对薄壁模型结果，厚壁管模型显示压力振荡周期和幅值均增大，流体模态频率和结构模态频率分别为6.44和17.72 Hz。此外，当输水管道厚径比<0.05，厚壁模型仍具有一定可靠性。该模型扩展和改进了常用薄壁模型，使其同时适用于厚壁管及薄壁管流固耦合分析。

压力；模型；水锤；流固耦合

0 引 言

管道运输流体已广泛应用于海洋工程、石油化工工程、能源与动力工业、航天器动力系统和日常生活中。管道内由于管内或管外受到多次激励而产生压力脉动，诱发管壁径向收缩或膨胀，材料泊松比导致管道明显轴向振动。同时，这些管路结构振动及流体压力脉动相互影响，这种现象叫做流固耦合（Fluid-Structure Interaction）。不同输水系统边界条件导致不同的FSI响应，故FSI响应分析必须根据不同边界条件进行逐案处理[1-4]。

管道与流体的耦合方式主要有摩擦耦合、泊松耦合和结合部耦合，其中摩擦耦合和泊松耦合贯穿整个管道，而结合部耦合只发生在靠近弯管、支管、阀门、边界、以及可变截面的管道中[5-7]，结合部耦合导致系统FSI响应更强[8-11]。此外，摩擦耦合的响应最弱，其作用水平在长期内逐渐降低[12]。同时，作为最重要的耦合形式，结合部耦合诱发更强的压力振荡，结合部耦合程度主要取决于系统的鲁棒性[13-14]。值得注意的是，泊松耦合对结合部耦合具有促进作用[15-16]。

上述文献流体管路的计算方法主要包括时域计算方法和频域计算方法，其中瞬态响应问题多采用时域计算方法求解，而对于自由或强迫振动响应则通常采用频域计算方法[17]。目前管道FSI响应计算常用的方法为特征线方法（Method of Characteristics，MOC）。但MOC是一种时域数值求解方法，适用于简单管路的时域响应计算，特别是流体压力波的瞬态响应分析[18]，因此在流体管路系统的时域分析中有非常多的应用，并得到不断完善，但特征线法需要在时间和空间中离散求解，较为复杂，且很难考虑管道的弹性支撑条件，多段管路计算时还存在插值误差和不同特征线的相交等问题。

有限体积法是一种介于有限差分法和有限单元法之间的一类数值求解方法。有限体积法基于守恒型积分方程，通过有限子区域积分构造离散方程。有限体积法求解问题具有2种方式，一种是控制体体积法，另一种是控制体平衡法。两者都描述了控制体物理量的守恒，所以有限体积法是一种无条件稳定的数值方法，且有限体积法不要求变量可微分，有限体积法的适应性广。

到目前为止，关于有限体积元法的理论成果已经相当丰富，很多国内外的早期研究成果被收录于文献[19]之中。为了避免有限体积法中离散格式中非物理振荡，Li等[19]提出了有限体积法中的迎风格式。这一格式是稳定的，且满足离散极值原理，然而该格式的数值精度却不是最佳的。在此基础上，Sardella[20]修正了有限体积法迎风格式，提高了计算精度。Liang等[21-22]分别提出了一种最优加权迎风有限体积法和二阶精度的有限体积法，进一步提高了计算精度。

当有限体积法应用于瞬变计算中，有限体积法的关键是在系统控制体积内积分，时间步长与控制体长度相互独立，故易于计算程序的编写。已有许多学者将有限体积法应用于瞬变流的研究中。Zhou等[23]利用有限体积法求解了含气水锤，说明了考虑气液两项流，有限体积法比特征线法更合适，且精度也能得到保证；耿艳芬等[24]基于有限体积法，建立了管道瞬变流的离散格式，采用特征分解技术计算界面通量，并通过重构和通量限制建立二阶精度的TVD格式保证了质量和动量的守恒性；赵修龙等[25]推导了C-N格式的有限体积法，并经过由特征线法数值结果的对比，说明了C-N格式的有限体积法稳定性好，且具有较高精度。这些有限体积应用成果为本文研究提供了基础。

为提高管道抗风险能力和延长有效运行时间，通常会使用厚径比较大的管道。但目前专家学者所关注均为薄壁管道输水系统，而几乎没有文献对厚壁管输水系统水力瞬变进行研究。厚壁管道轴向应力沿径向变化不可忽略，但已有薄壁管计算模型不考虑轴向应力沿径向变化。针对瞬变流的流固耦合问题，已有模型分析厚壁管可能获得更大的系统鲁棒性，同时获得不准确的模态响应。为了更准确的捕捉厚壁管在瞬变过程中的水力特性和管道振动特性，本文假设管道可以在其纵向自由振动、径向加速度可忽略不计、且厚壁管沿径向具有不同的轴向应力。基于已有薄壁管分析模型（薄壁管流固耦合模型或薄壁模型），建立并提出了适用于厚壁管流固耦合一维模型，模型包括采用流体运动方程、流体连续方程、管壁运动方程和管壁本构方程，也可称为厚壁管流固耦合4方程模型或厚壁模型。模型采用有限体积法求解。

1 数学模型

输水系统轴向耦合响应与输水管线所处侧向平面及扭转耦合是可以解耦的[15]，故可单独对管道输水系统轴向流固耦合进行分析。厚壁管示意图如图1所示。

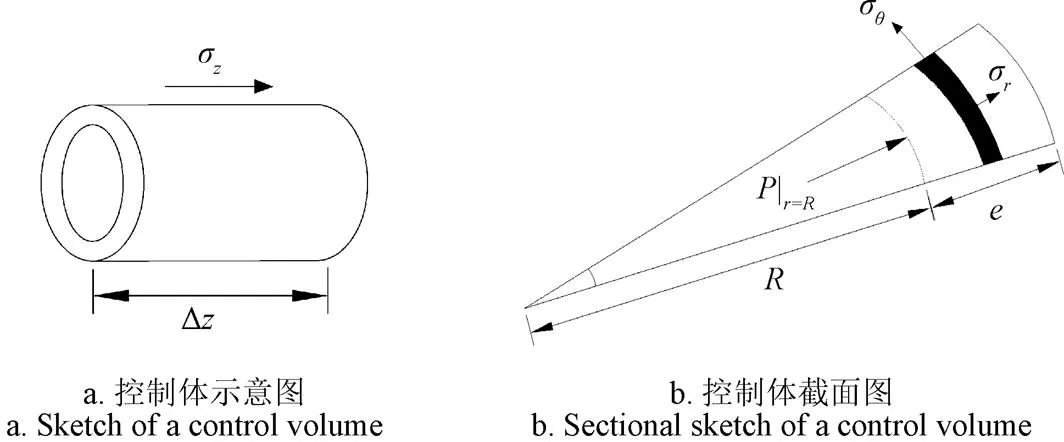
注：P|r=R为管壁内表面压力，Pa；σz为管壁轴向应力，Pa；σr为管壁径向应力，Pa；σθ为管壁环向应力，Pa；R和e分别为管道内径和壁厚，m；Δz为控制体长度

1.1 流体控制方程

1.1.1 流体运动方程

忽略流体环向流速，且不考虑流体科氏力[18]，则不可压缩流体运动方程：

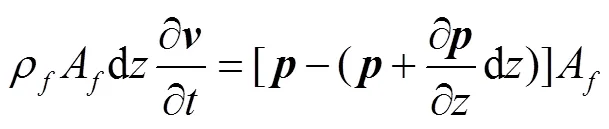
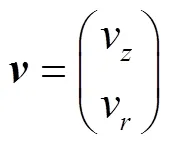
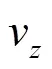
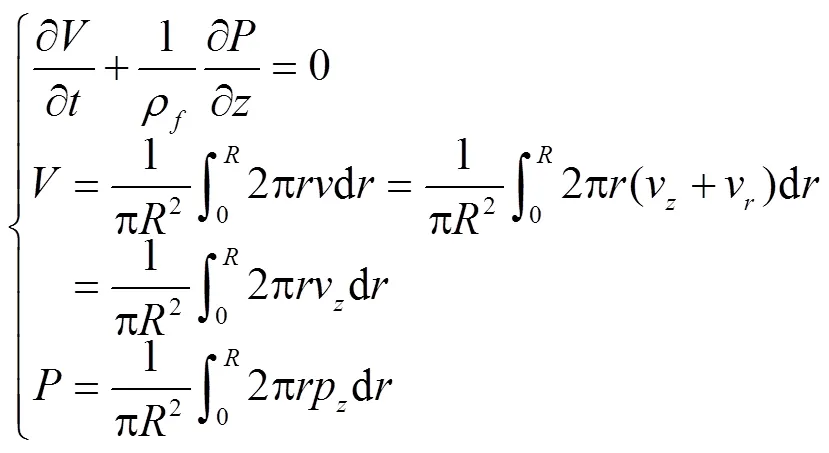
式中为流体截面平均流速，m/s；为流体截面平均压力，Pa；表示管道输水系统径向坐标。

1.1.2 流体方程

对于不可压流体，其轴对称流动的连续方程为

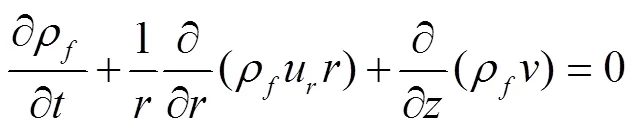
式中u为管壁径向振速，m/s，沿管壁径向具有不同的结果。由水锤波速∂/∂A=/ρ，为流体体积模量，Pa；将∂/∂A=/ρ代入方程（3）。为将方程（3）表示的二维流动问题简化为一维，对方程（3）两边乘以2，从管芯到管壁求积分，然后除以流体截面面积。引入流体截面参量的平均值，化简得到：

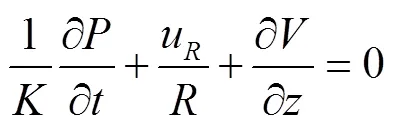
考虑流固耦合，管道内表面环向应变为ε|=w/，w为管壁内表面径向位移，m。则u/=∂ε|/∂，其中u为管壁内表面径向振速，m/s。

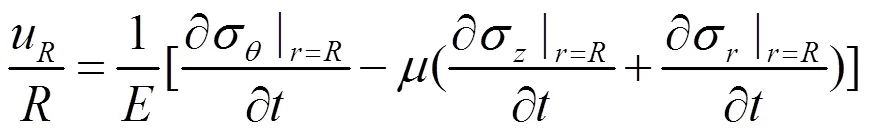
式中为管材弹性模量，Pa；为管材泊松比。管壁环向应力与径向应力的拉梅解形式[17-18]

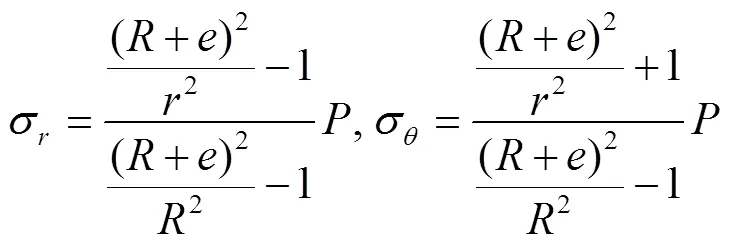
且轴向平均应力与轴向应力定义为[18]

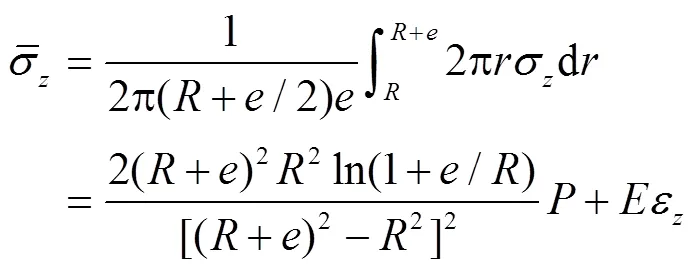
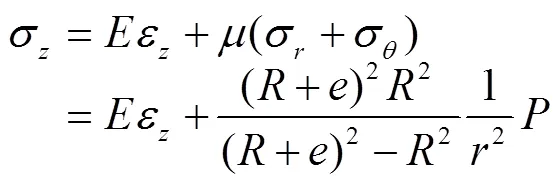
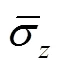
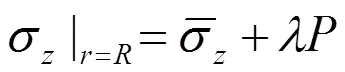
式中被称为应力削减系数，的定义表达式为

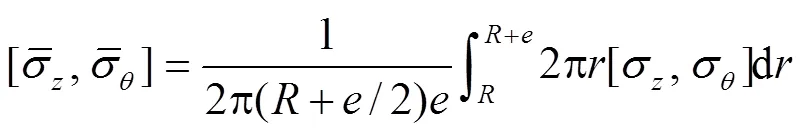
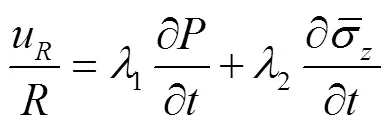
将方程（10）代入方程（4），得到考虑流固耦合下厚壁管输水的不可压缩流体连续方程：

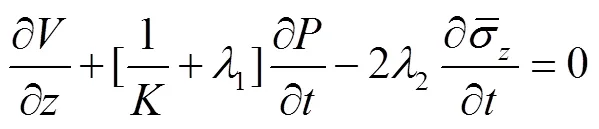
1.2 管壁控制方程

1.2.1 管壁运动方程

考虑厚壁管材料是弹性，且管壁不受外力情况，管道运动方程为[26-27]

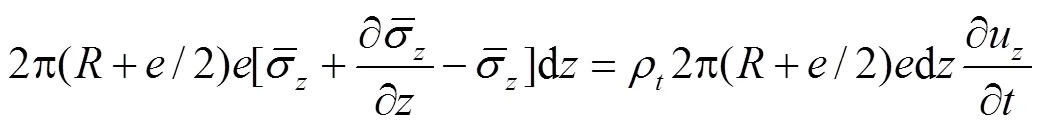
方程（13）简化为

式中u为管道轴向振速，m/s。

1.2.2 管壁本构方程

针对给定的输水管道，管道轴向应变与应力关系表达式为：

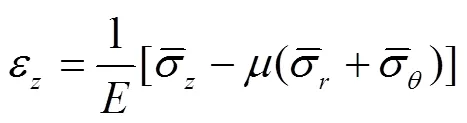
根据方程（3），截面径向与环向平均应力之和为

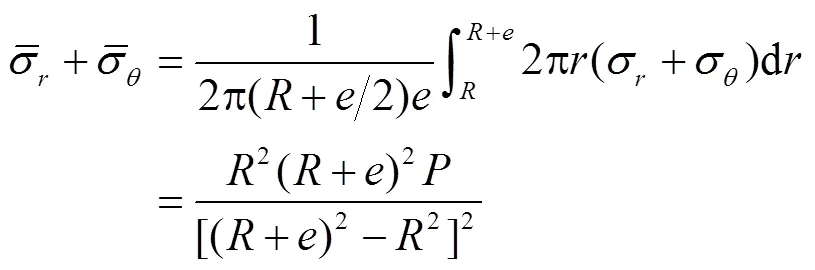
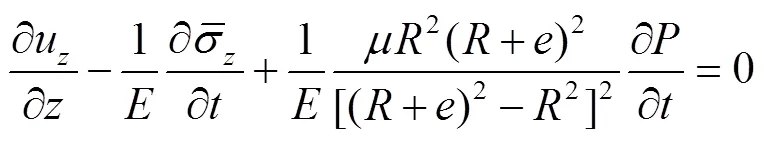
2 数值求解

考虑输水管道为厚壁管，则结构径向变形不可忽略，考虑结构径向变形，管道状态及流体状态是二维的，取截面平均值进行分析和推导，基于薄壁管流固耦合分析模型（薄壁模型），建立了适用于厚壁管流固耦合分析的一维模型。模型包括的流体运动方程、流体连续方程、管壁运动方程和管壁本构方程，分别如方程（2）、方程（12）、方程（14）和方程（17）所示，这些方程统称为厚壁模型。

有限体积法求解时是对每个控制容积进行积分求解有限体积，且积分方程中每一项的物理意义明确[28]，因此，本文采用有限体积法计算分析管道FSI响应。有限体积法利用控制容积积分来实现方程的离散[29]，在控制容积内从时间到Δ对连续方程积分[30]，根据C-N隐式差分方法[31]，方程（2）、方程（12）、方程（14）和方程（17）矩阵形式为：

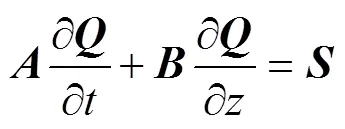
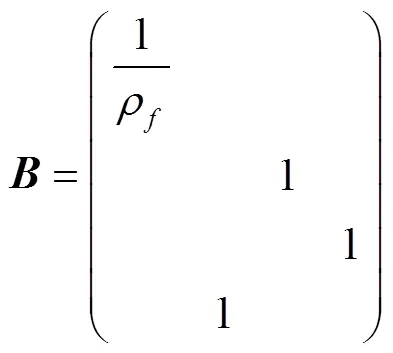
对有限体积法而言，控制体简化为线。在控制体内对时间和空间的积分为：

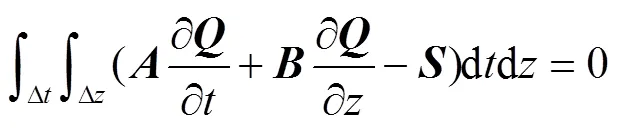
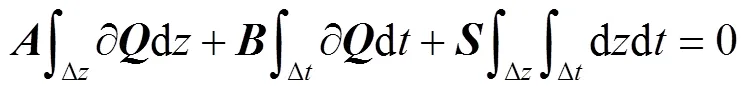
当时间步长和控制体长度足够小，则取近似值：

则方程（20）离散为

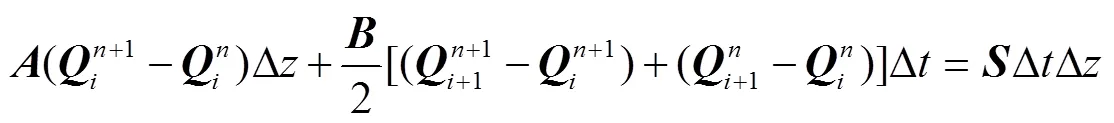
得到控制体相邻时步的迭代方程为

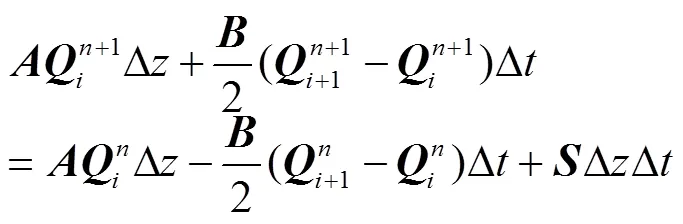
由方程（22）可得到，所有控制体组成了输水系统，其相邻时步状态的迭代方程为

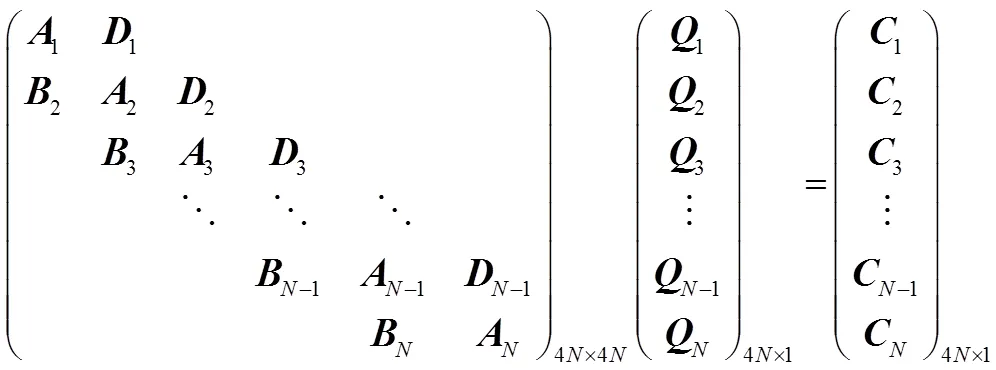
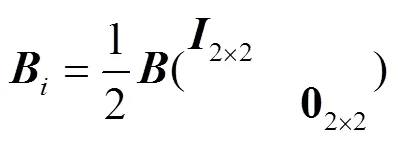
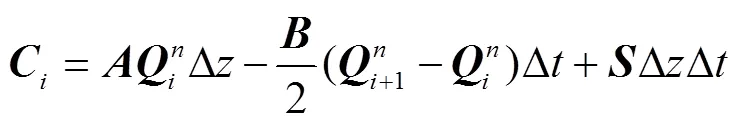
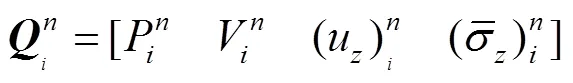
Δ为有限体积法计算时步步长，Δ为控制体积长度，表示第时步，表示第个控制体，第个控制体在第时步系统状态矩阵，是第个控制体在第+1时步的系统状态矩阵。在本文计算中，= 1表示流体入口，=表示流体出口。在计算第+1时步状态时，是已知矩阵。

3 分析与讨论

3.1 验证

为了验证厚壁管道数学模型的正确性，本文采用厚壁模型预测了一段自由管在实心钢棒撞击下的撞击端和远端瞬态压力，并与英国邓迪大学土木工程系Vardy等[32]获得的试验数据作对比。预测的物理模型和Vardy等的试验装置均为一根长4.5 m钢管，管道系统两端封闭，并设置堵头。为了更接近管道自由状态，故管道悬挂布置。管道系统引起瞬变的荷载是由长为5.006 m的实心钢棒轴向撞击管道的闭合端而产生，如图2所示。瞬变产生的边界方程为

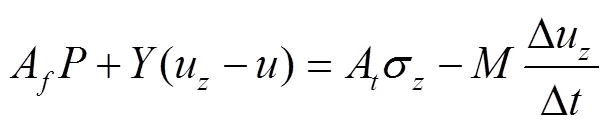
式中为钢棒冲击阻尼，N/(m/s)；为冲击端堵头质量，kg；为实心钢棒对管道的撞击速度，m/s。撞击发生之前，管道为初始状态，此时的初始管内初始压力为2 MPa；初始流速为0；管道内无压力梯度，故管壁应力与振速均为0。当撞击发生后，采用方程（23）迭代得到Δ时的系统瞬变状态。值得注意的是为了结果的精确性，Δ=10-4s、控制体长度为Δ=0.1 m。

注：为实心钢棒对管道的撞击速度，m·s-1。

Note:is Impact velocity of solid steel bar on pipe, m·s-1.

图2 文献[32]试验装置

Fig.2 Sketch of experimental setup in reference [32]

管道内压为大气压的情况下，展示了冲击管道产生的管道撞击远端和撞击端压力脉动数值结果和试验结果，如图3所示。

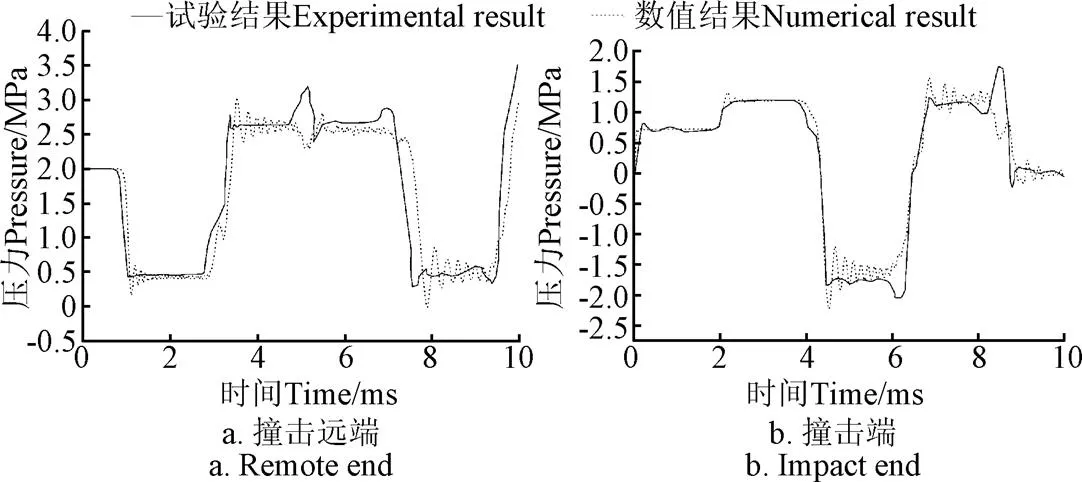
图3 试验系统动态压力

根据图3中数值结果与试验结果对比，明显可观察到数值结果中叠加有高频的压力振荡，说明了数值结果能够得到更精确的压力振荡过程。这种现象可解释为试验采样频率为80 Hz[15]时，忽略了输水管道的高频特性，而数值计算的时间步长为10-4s，能够很好地捕捉压力振荡的高频信号。然而，由图3可知，在冲击远端第一波压力数值结果与试验结果峰值分别为3.22和3.33 MPa，两者相对误差为−3.3%；在冲击端第一波压力峰值数值结果与试验结果分别为3.34和3.19 MPa，两者相对误差为4.5%。相对误差均在−5%～5%以内，且试验结果与数值结果具有相同的趋势，说明本模型适用于描述水锤作用下厚壁管流固耦合分析，且有限体积法求解厚壁管流固耦合问题是合理的。同时，数值结果仅考虑轴向振动，试验结果则包括了多方向的耦合形式。但两者结果误差在容许范围内，说明了在瞬变过程中，管道振动主要为轴向振动，则轴向耦合为主要耦合。

3.2 工程实例

3.2.1 耦合水锤分析

实际工程中，厚壁管输水系统是常见的，但一般具有多支承的特点。为进一步说明厚壁模型的应用价值，分析了多支承管输水系统。本管道输水系统是由河海大学水力发电中心所实施，采用型号为HQ1000的压力传感器记录了阀门前端瞬态压力。其中管道为厚壁管，管道长=20 m，每跨跨长为4 m，管道内径=0.06 m，管壁总厚度=0.006 m，初始压力为1 m水头，初始流速为1 m/s。初始时刻，管内无压力梯度，故管道轴向应力和轴向振速均为0。输水系统示意图如图4所示。系统的瞬变激励为快速关阀，关阀过程阀门开度变化为(1-/)1.5，为总关阀时间，s。为保证关阀规律的准确性，本系统采用机器控制阀门开度。

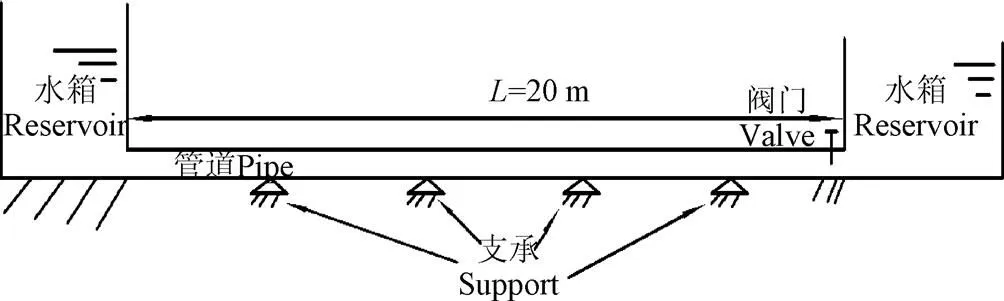
注：L为管道长度，m。

输水系统中瞬变激励为快速关阀，厚壁管为弹性结构，且在水锤荷载作用下膨胀或收缩，产生新的压力振荡，2种压力振荡相互叠加，得到考虑流固耦合的压力振荡[33]。根据文献[15]，支承考虑为弹性支承，忽略支承惯性，支承的边界条件为

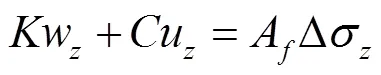
式中为支承轴向弹性系数，N/m；为支承阻尼，N/(m/s)；Δσ为支承相邻两控制体积中轴向应力改变量，Pa。

边界考虑结构径向与轴向约束，流固耦合响应对系统模态频率具有较大影响，频率均小于1 000 Hz[34]。综合考虑数值分析得到实际压力振荡信号的完整性和计算耗时，计算时间步长Δ、控制体长度Δ分别为0.001 s、0.1 m。

为了显示厚壁模型与薄壁模型的区别，分别采用厚壁模型、薄壁模型和经典水锤模型模拟简单的多支承输水系统，考虑流固耦合，得到的力振荡如图5所示。相对仅考虑流体因素的两方程模型，考虑流固耦合，压力振荡与多因素相关，结果也更加复杂，结果表现为多个压力振荡的叠加，且曲线上存在多处局部峰值，这种现象可解释为，当不考虑流固耦合，等效为管道是刚性的，管道变形引起的高频压力振荡被忽略。相对薄壁管模型假设轴向应力沿径向为一常数，厚壁模型考虑了轴向应力沿径向变化，截面应力平均值小于在流体结构交界面的轴向应力。故相对于传统的薄壁模型，厚壁模型得到的耦合响应较弱，压力波速较小，表明系统柔性较小。

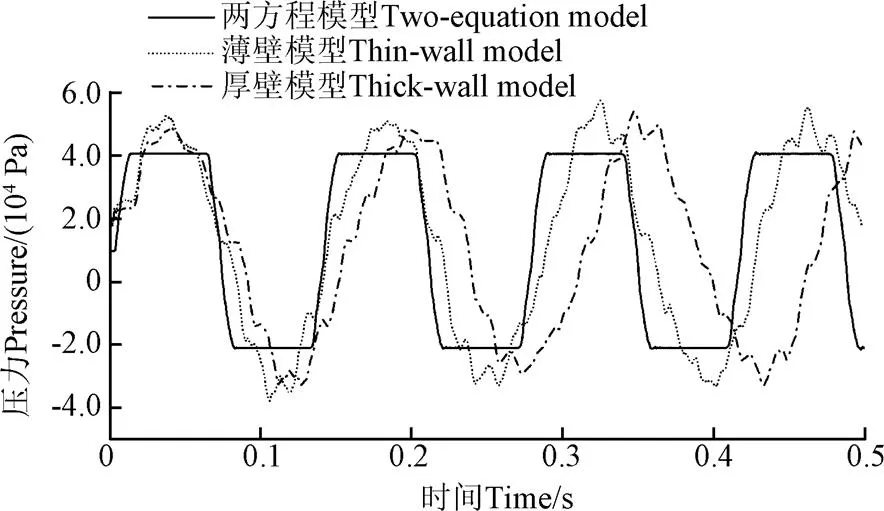
图5 不同模型下的数值模拟压力

与经典二方程模型的数值分析结果比较分析，无论薄壁模型还是厚壁模型，管道的轴向耦合形式包括泊松耦合和结合部耦合。此时，系统中存在沿轴向传播的应力波和压力波。本算例中，厚壁模型计算得压力波波速和应力波波速分别为1 348和4 113 m/s，应力波速约为压力波速的3倍。则考虑流固耦合时，压力脉动峰值可分为3部分进行分析：在第一部分中，考虑泊松耦合和结合部耦合，水压剧烈上升引起管壁径向膨胀和管道出口端轴向移动，释放了压力振荡能量，产生第一个压降，同时，管壁径向膨胀和管道出口端轴向移动导致管道变形以应力波形式传播；在第二部分中，管壁为收缩状态，对不可压缩流体进行了压缩，对流体的影响类似于输水泵的作用，因此压力峰值比经典模型模拟结果大；在第三部分中，轴向应力波反弹，管壁再次扩张，在压力波动上产生最后一个压降。上述现象反复出现，形成图5所示的压力振荡。图5显示，当考虑流固耦合，水锤能量被管道吸收，管道显示更大的柔性。此时，管道波速减小，压力振荡大周期增大（=4/c，c为水锤波速）。且厚壁模型与薄壁模型得到不同的耦合响应，对波速也具有不同的影响。

3.2.2 压力波传播速度

根据文献[35]，可知输水系统的波速（包括应力波和压力波）定义为

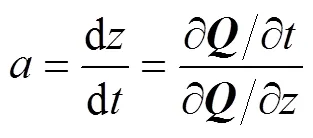
则考虑流固耦合的波速方程可定义为

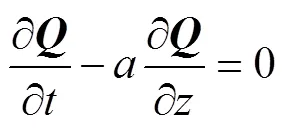
将方程（27）代入方程（18），可得

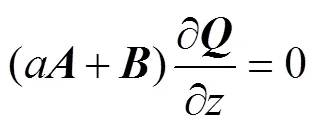
为了得到非零解，则

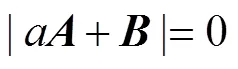
求解方程（29），得到应力波速与压力波速相容性方程：

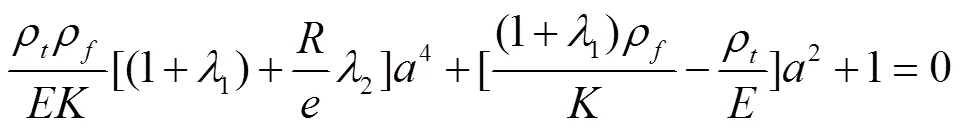
方程（30）简化为

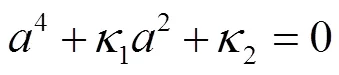
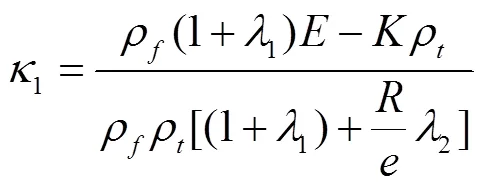
求解方程（31），得到2个正根即为压力波速的平方值c2和应力波速的平方值c2。

为了验证波速的数值结果，进行了试验，试验装置如图4所示。在3.2.1所述试验基础上，仅改变管道的厚径比。同时，压力传感器HQ1000由频率50 kHz的压力传感器替代，采样频率为1 000 Hz。采集了不同厚径比管道阀门附近的动态压力，并由此得到不同的波速，试验结果如图6所示。

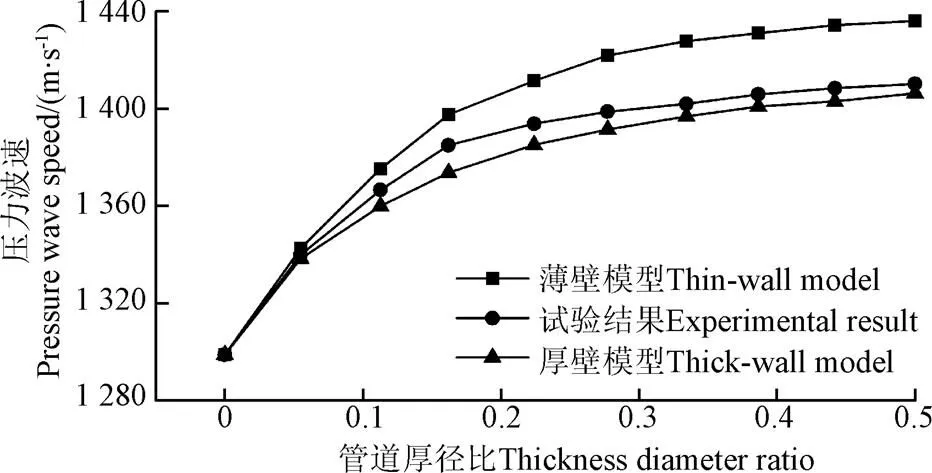
图6 输水系统波速随厚径比的变化趋势

压力波在水中的传播速度与输水系统鲁棒性相关[29-30]，而系统鲁棒性与管道厚径比密切相关，通过不同厚径比情况下压力波速和应力波速的分析讨论表明：系统鲁棒性越大，压力波速就越大，同时获得更小的应力波速，反之亦然，结果如图6所示。由图6可知，厚壁模型和薄壁模型模拟结果与试验结果相对差值最大分别为1.3%和4.6%。说明模拟流固耦合响应时，厚壁模型得到更可靠的结果。

当/=∞，输水系统鲁棒性足够大，系统流固耦合可忽略，求解方程（30）得到c=1 414 m/s。当/=0.5，c= 1 400 m/s，相比于不考虑流固耦合，波速的偏差为0.98%，则当/0.5时，大的系统鲁棒性导致弱的流固耦合响应。上述现象说明：当/>0.5时，两方程模拟系统是合适的，同时，薄壁模型与厚壁模型模拟结果具有较大的差别；当/0.05，薄壁模型与厚壁模型模拟结果差别可忽略，即当/0.05时，薄壁模型是合适的。上述分析结论也进一步证明本文所建立厚壁模型的正确性。

3.2.3 管道振动分析

不考虑流固耦合响应，系统模态分为流体模态和结构模态。考虑流固耦合响应，所有的振动模式都是系统模式。管道变形分析能够明显观察到结构模态和流体模态，通过数据处理，可识别管道变形模式与结构或流体均密切相关。在多支承输水系统中，只有压力波和应力波沿系统轴向传播。考虑到流固耦合，图7虚线所示的结果清楚地表明，厚壁模型预测得到的频率6.44和17.72 Hz均归因于水柱和钢管的固有频率，其中频率6.44 Hz对应管壁变形的呼吸模式（管壁呼吸模态频率等于水柱固有频率）。图7实线所示薄壁模型预测得到的频率6.68和17.34 Hz亦归因于水柱和钢管的固有频率。图7中，每个频率峰值表示流体或结构的基波和奇次谐波。

相对于薄壁模型，厚壁模型考虑了轴向应力削减效应（方程（9）所示），导致管壁轴向位移沿径向变化，管壁不同径向位置相互拉伸或压缩。此时，管道轴向的势能增加，这些管道势能来自由水锤能量，即厚壁管模拟结果显示结构消耗更多的水锤能量。此时，管道振动更强烈，压降和“泵”效应更加明显，即更强烈的流固耦合响应，如图5所示。这些现象都进一步增大结构轴向变形水平，故厚壁模型获得更大模态峰值，如图7所示。当厚壁模型得到更大的振动水平，系统显示更小鲁棒性，最终导致流体模态频率减小。这种现象在更高频的模态中显得更加明显，如图7所示。

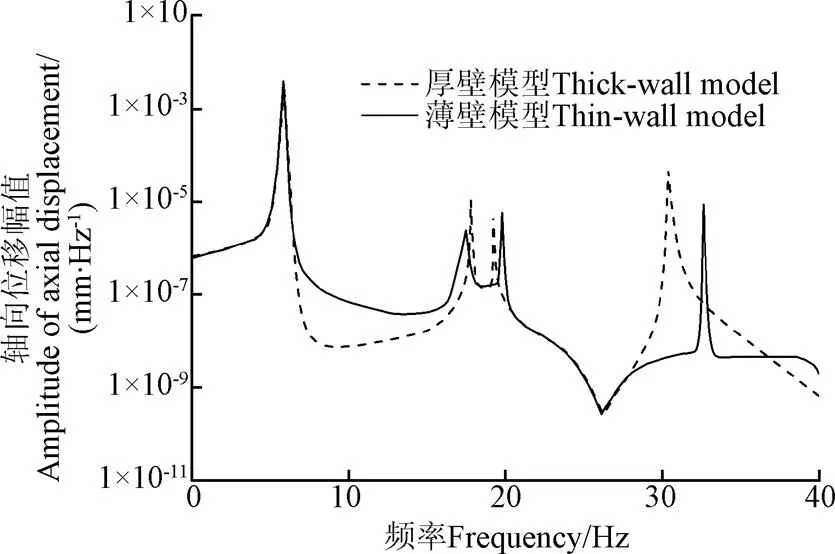
图7 管壁在频域内的变形水平

4 结 论

发生于厚壁管输水系统中的水锤现象长期以来一直是一种难以理解的现象。为了研究水击作用下厚壁管的耦合响应，基于流体控制方程和结构本构方程，基于薄壁模型，建立了适用于厚壁管流固耦合分析的一维模型。将有限体积法应用于该模型的求解，结果表明数值结果与试验结果吻合较好。这种模型考虑了管壁弱化了管道轴向应力水平，当管壁足够薄时，这种影响可以忽略不计。在这种情况下，厚壁模型退化为公认的薄壁模型。

为揭示2种模型的差异，对模型预测结果进行了对比，进一步得到以下结论：

1）考虑流固耦合，管道的变形对流体起着泵效应或松弛效应，导致流体压力脉动曲线出现较多局部突变。但厚壁模型结果显示压力振荡和管道轴向振动具有更高的水平，即厚壁管获得更强烈的耦合响应。同时，对比试验波速结果，说明了厚壁管模型结果更可靠。

2）在瞬变过程中，厚壁管轴向应力沿径向减小，导致管内更强烈的压力振荡，且导致压力振荡周期变大。效应随管壁厚度减小而变弱，当厚径比/<0.05时，这种效应可忽略，则厚壁模型退化为薄壁模型。对于给定的厚壁管，当/>0.05时，厚壁模型预测分析结果具有更大可靠性，能准确揭示系统具有较大的柔性和较小的压力波速。

3）考虑流固耦合，在瞬变过程中，系统所有模态均由压力波和应力波导致的。相对于薄壁模型，厚壁模型结果显示更低频的流体模态和更高频的结构模态。

[1] Spinosa E, Iafrati A. Experimental investigation of the fluid-ftructure interaction during the water impact of thin aluminium plates at high horizontal speed[J]. International Journal of Impact Engineering, 2020, 24: 563-586.

[2] Sun T Z, Zhou L, Yin Z Y, et al. Cavitation bubble dynamics and structural loads of high-speed water entry of a cylinder using fluid-structure interaction method[J]. Applied Ocean Research, 2020, 101: 1-12.

[3] Abdalellah O M, Hussain H A K, Osman A B, et al. One-way coupled fluid–structure interaction of gas–liquid slug flow in a horizontal pipe: Experiments and simulations[J]. Journal of Fluids and Structures, 2020, 97: 103083.

[4] Li S, Liu G, Kong W. Vibration analysis of pipes conveying fluid by transfer matrix method[J]. Nuclear Engineering and Design, 2014, 266: 78-88.

[5] Wahba E M. On the two-dimensional characteristics of laminar fluid transients in viscoelastic pipes[J]. Journal of Fluids and Structure, 2017, 68: 113-124.

[6] Wang X J, Lin, A. Keramat, M S, et al. Matched-field processing for leak localization in a viscoelasticity pipe: An experimental study[J]. Mechanical Systems and Signal Processing, 2019, 124: 459-478.

[7] Ghodhbani A, Akrout, A, Hajtaïeb T. Coupled approach and calculation of the discrete vapour cavity model[J]. Journal of Fluids and Structures, 2019, 91: 787-804.

[8] Keramat A, Moghadam F M, Zanganeh R, et al. Experimental investigation of transients-induced fluid-structure interaction in a pipeline with multiple-axial supports[J]. Journal of Fluids and Structures, 2020, 93: 884-910.

[9] Zanganeh R, Jabbari E, Tijsseling A, et al. Fluid-structure interaction in transient-based extended defect detection of pipe walls[J]. Journal of Hydraulic Engineering 2019, 82: 733-752.

[10] Wang X, Ghidaoui M S, Lin J. Identification of multiple leaks in pipeline III: Experimental results[J]. Mechanical Systems and Signal Processing, 2019, 130: 395-408.

[11] Keramat A, Wang X, Louati M, et al. Objective functions for transient-based pipeline leakage detection in a noisy environment: Least square and matched-filter[J]. Journal of Water Resources Planning and Management, 2019, 112: 1106-1123.

[12] Yang K, Li Q S, Zhang L X. Longitudinal vibration analysis of multi-span liquid-filled pipelines with rigid constraints[J]. Journal of Sound and Vibration, 2012, 273: 125-147.

[13] Tijsseling A S. An overview of fluid-structure interaction experiments in single-elbow pipe systems[J]. Journal of Zhejiang University: Science A, 2019, 20: 233-242.

[14] Matthew H, Vakhtang T, Randy S J, et al. Fluid–structure interaction modeling in cardiovascular medicine–A systematic review 2017-2019[J]. Medical Engineering and Physics, 2020, 78: 1-13.

[15] Zhang L, Tijsseling A S, Vardy A E. FSI analysis of liquid-filled pipes [J]. Journal of Sound and Vibration, 1999, 224: 69-99.

[16] Tijsseling A S, Vardy A E. 20 years of FSI experiments in Dundee[C]//Proceedings of the Third M.I.T. Conference on Computational Fluid and Solid Mechanics, Massachusetts Institute of Technology. New York: MA, 2015: 1-8.

[17] Henclik S. Numerical modeling of water hammer with fluid-structure interaction in a pipeline with viscoelastic supports[J]. Journal of Fluids and Structures, 2018, 76: 469-487.

[18] David F, Pedro A, Anton J, et al. Fluid-structure interaction in straight pipelines with different anchoring conditions[J]. Journal of Sound and Vibration, 2017, 394: 348-365.

[19] Li R, Chen Z, Wu W. Generalized Difference Methods for Differential Equations: Numerical Analysis of Finite Volume Methods[M]. New York: Marcel Dekker, 2000: 16-49.

[20] Sardella M. On a coupled finite element-finite volume method for convection-diffusion problems[J]. IMA Journal of Mumerical Analysis, 2000, 20: 281-301.

[21] Liang D, Zhao W. An optimal weighted upwind control volume method on non-standard grids for convection- diffusion problems in 2D[J]. International Journal of Numerical Method Engineering, 2006, 67: 553-577.

[22] Salvador B L, Alejandro A P S, Wang Z F, et al. Strain-engineering of graphene's electronic structure beyond continuum elasticity[J]. Solid State Communications, 2013, 166: 71-75.

[23] Zhou L, Wang H, Liu D Y, et al. A second-order Finite Volume Method for pipe flow with water column separation[J]. Journal of Hydro-Environment Research, 2017, 17: 47-55.

[24] 耿艳芬，王志力，金生. 基于有限体积水锤方程的Go-dunov格式离散[J]. 计算力学学报，2007，24(4)：513-518.

Geng Yanfen, Wang Zhili, Jin Sheng. A Godunov method for water hammer problem based on finite volume method[J]. Chinese Journal of Computational Mechanics, 2007, 24(4): 513-518. (in Chinese with English abstract)

[25] 赵修龙，张健，俞晓东. 基于有限体积法的有压管道水锤计算[J]. 水电能源科学，2014，32(2)：164-166.

Zhao Xiulong, Zhang Jian, Yu Xiaodong. Finite volume method for water hammer calculation in pressure pipe[J]. Water Resource and Power, 2014, 32(2): 164-166. (in Chinese with English abstract)

[26] Li G L, Du S C, Huang D L, et al. Elastic mechanics-based fixturing scheme optimization of variable stiffness structure workpieces for surface quality improvement[J]. Precision Engineering, 2019, 56: 343-363.

[27] 徐芝纶. 弹性力学（第四版）[M]. 北京：高等教育出版社，2006：257-412.

[28] Luis R, Nogueira X, Pablo O, et al. A Higher-Order Chimera Method for Finite Volume Schemes[J]. Archives of Computational Methods in Engineering, 2018, 25: 691-706.

[29] HwangY H, Chung N M.A fast Godunov method for the water-hammer problem[J]. International Journal for Numerical Methods in Fluids, 2002, 40: 799-819.

[30] Cao H D, Mohareb M, Nistor I. Finite element for the dynamic analysis of pipes subjected to water hammer[J]. Journal of Fluids and Structures 2020, 93: 984-996.

[31] Daude F, Tijsseling A S, Galon P. Numerical investigations of water-hammer with column-separation induced by vaporous cavitation using a one-dimensional Finite-Volume approach[J] Journal of Fluids and Structures 2018, 83: 91-118.

[32] Vardy A E, Fan D, Tijsseling A S. Fluid-Structure Interaction in a T-piece pipe[J]. Journal of Fluids and Structures, 1996, 10: 763-786.

[33] 张春晋，孙西欢，李永业，等. 基于流固耦合的管道双车振动运移水力特性研究[J]. 振动与冲击，2020，39(3)：161-167.

Zhang Chunjin, Sun Xihuan, Li Yongye, et al. Hydraulic characteristics of a piped double-carriage’s vibrational transport based on fluid-structure interaction[J]. Journal of Vibration and Shock, 2020, 39(3): 161-167. (in Chinese with English abstract)

[34] 王振华，马习贺，李文昊，等. 基于改进4-方程摩擦模型的输水管道水锤压力计算[J]. 农业工程学报，2018，34(7)：114-120.

Wang Zhenhua, Ma Xihe, Li Wenhao, et al. Calculation of water hammer pressure of flow pipeline based on modified four-equation friction model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 114-120. (in Chinese with English abstract)

[35] Wylie E B, Streeter V L. Fluid Transient in System[M]. Now York: Prentice Hall, 1983: 14-24.

Water hammer and vibration analysis of a thick-wall pipe considering fluid-structure interaction

Guo Qiang, Zhou Jianxu※, Huang Ya, Zhang Jian

(,,210024,)

A thick-wall pipe is widely used in a water conveyance system, due to its high anti-risk ability on transient flow. If the thickness of pipe wall is great enough, the axial stresses vary significantly in the radial direction. It is necessary to consider a buffering effect of axial stresses, representing by the buffering coefficients1and2. In this study, an one-dimensional Fluid-Structure Interaction (FSI) model was proposed for the accurate prediction on the mechanical properties of a thick-wall pipe during water hammer. A FSI thin-wall model was also set considering the relaxed effect that caused by the radial deformation. Four equations included the continuity and motion equation of fluid, while, the motion and deformation equation of pipe structure. A Finite Volume Method (FVM) was also selected to evaluate the reliability and accuracy of the model, according to the experimental data. Compared with the thin-wall model, the thick-wall model can be used to weaken the axial stress level in the pipe wall under buffering effects. The simulated results showed that there were obvious buffering effects, and evident differences between the thick- and thin-wall model, at the thickness-diameter ratio of/>0.05. At the thickness-diameter ratio of/<0.05, there were the minor buffering effects, and the negligible differences between the thick- and thin-wall model.In the small values of coefficients1and2, the thick-wall model can be degenerated into the thin-wall model. It infers that the thin-wall model can be assumed as the special mode of thick-wall model without buffering effects. Considering FSI, the first pressure drop, ‘pumping’ effect, and last pressure drop can be observed in each half period, indicating an important role in the modes of fluid or structures.There were totally differences in the pressure oscillation, wave speeds, and axial vibration of pipe wall. Specifically, all the modes of frequencies were attributed to the speed of pressure wave and stress waveThe resulting structure or fluid behaved different mode responses. The waves was dominated in the simulated and experimental data that derived from the pressure wave speeds in two models, indicating that the thick-wall model was much more accurate for a thick-wall pipe during water hammer. In addition, the axial vibration and pressure oscillation became stronger in the thick-wall model, indicating that the system has stronger FSI responses. In the modes with low frequencies, the system displayed relatively low robustness, where the fluid can suffer to the slow ‘pumping’ effect. A given system simulated by the thick-wall theory demonstrated a large flexibility and small pressure wave velocity. The modified thick-wall model can be used to significantly improve the fluid-structure interaction model for a thick-wall pipe.

pressure; models; water hammer; fluid-structure interaction

郭强，周建旭，黄亚，等. 考虑流固耦合的厚壁输水管水锤和振动特性分析[J]. 农业工程学报，2020，36(21)：137-144. doi：10.11975/j.issn.1002-6819.2020.21.017 http://www.tcsae.org

Guo Qiang, Zhou Jianxu, Huang Ya, et al. Water hammer and vibration analysis of a thick-wall pipe considering fluid-structure interaction[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(21): 137-144. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.21.017 http://www.tcsae.org

2020-07-26

2020-08-31

国家自然科学基金（51879087，51839008，51709087）作者简介：郭强，博士，主要从事瞬变过程的研究。Email：guoq1228@126.com

周建旭，教授，博士，主要从事水电站水力瞬变研究。Email：jianxuzhou@163. com

10.11975/j.issn.1002-6819.2020.21.017

TV134

A

1002-6819(2020)-21-0137-08