换元法在高中数学解题中的应用

王凤梅

(山东省青岛市城阳区第一高级中学 266108)

换元法作为高中数学具体教学中，较为常见的一种解题方法，在数学的解题中，通常会出现较为复杂或存有两个及其以上的未知条件的相关数学题，在解题的时候，可依据知识之间存在的内在联系，对数学题中存有的数量关系实施转化，并通过各变量的条件转换，将一种问题转变成另种问题，以实现整个解题的简化.同时，换元方法有许多种，如函数换元、变量换元、不等量换元、三角函数的换元等.在具体解题的时候，教师通过换元法的灵活应用，不仅能够对学生自身的思维敏捷度进行锻炼，而且还能使学生自身的思维能力得到有效提高.

一、换元法内涵及其应用技巧归纳

1.换元法内涵

所谓的换元法，其主要就是把数学题目中原先的部分变量通过另一些变量进行替代，经过换元，通常能够产生缩减变量、简化形式的效果.较为常见的换元方式包含三种，具体为：(1)整体换元，如将x表达式的f(x)进行整体替换成t，并通过t表示成其他的与x有关的表达式；(2)利用关系，其主要指将较为相似的表达式进行换元，其主要是通过已知代数式和三角知识的联系实施换元，也就是在解题的时候，通过相同的参数，对两个变量进行表示，以减少变元，促使问题简化；(3)均值换元，当能够确切求出两个变量和的时候，就能通过均值换元.不论是何种换元，在换元之后，都能够对新变量实施运算，在对变量完成计算后，再对原变量进行取值，通过这样的解题思路，需确保换元时的等效变换，特别是定义域转变，只有确保变换的等效，才能确保计算结构的有效性.

2.应用技巧归纳

首先，常规换元法的掌握.对于不同换元法，其通常具有相应的形式，特别是三角换元.因此，对于难度较低的题目，学生只要充分掌握较为常规化的换元规律，并做出迅速反应，就能实现迅速解题.

其次，注重题目形式的观察.对于难度相对较高的数学题型，其题目的条件通常具有较强的隐藏性，此时，就需对题目条件实施相应的梳理与分析，并找到换元实施的突破点.需要注意的是，题型的难度通常不会对换元的相关条件造成影响，因此，对条件实施初步解算以及分析，不仅有利于学生打开解题思路，而且还能实现高效解题.

最后，注意等效的条件.应用换元法的前后，其等效性通常是其正确应用的重要保证，但也是在解题中最容易被忽略的部分.不论是哪种题型，难度如何，都需对等效性进行牢固记忆.

二、换元法在高中数学解题中的应用策略

1.基于换元法的三角函数教学

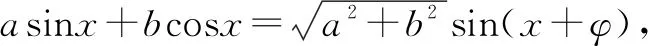
例1 已知x、y满足x2-xy+y2=1，求x2-y2的取值范围.

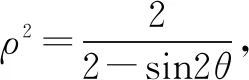
2.基于构造辅助的函数换元

基于构造辅助的函数换元属于极其重要的一种解题方法.对于函数而言，其作为高中数学具体教学中的核心知识，通常具有相应的导向性与工具性，大部分问题都能够以巧妙的构造进行函数辅助，促使复杂难解的问题转变为直观明了，转变为程序化.

解若m=1，a<0的时候，f(x)=x-aInx-1，x∈(0,+∞).

通过构造辅助函数方法，对具体问题进行分析，明确原问题和和辅助函数之间的联系，并通过相应的推理，构造出合理的辅助函数，从而对问题进行有效解决.

3.基于换元法的不等式解题

不等的证明与解答相关问题属于高中数学中的重要模块，通过换元法，对题实施新元替换，不仅有助于学生解题思路进行梳理，而且还能实现高效解题.

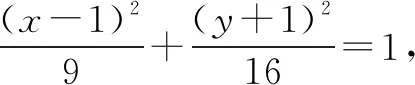
在实际解题中，经过换元法进行新不等式的构建，不仅使解题思路得到有效简化，而且还能促使解题方式实现简便化，这对不等式相关问题解答是个重要突破口，也是一种高效的解法.

综上所述，高中数学的具体教学中，换元法属于较为常见的一种解题方法，其不仅指解题过程的简化，而且还有助于学生形成良好的解题思路，并形成发散思维，同时，灵活的应用各种换元法，还能使繁琐且复杂的数学问题实现简化计算.