船舶航向最小方差自校正控制技术研究

郭亦平 林莉 孙灵远 潘攀

（天津航海仪器研究所九江分部，九江，332007）

航向自动控制一直是船舶操纵的主要模式之一，航向自动控制算法是保证自动舵实现航向保持和航向改变的核心。航向控制算法也是国内外船舶操纵自动化研究人员长期关注并持续研究的重要算法。Kallstrom和 Astrom 利用间接自校正控制理论开发的自适应航向控制算法[1]。Hung D Nguyen研究开发了自校正极点配置航向控制算法和最小方差自校正控制算法，完成了海试验证，但结果表明其设计的自校正控制算法有时会失去航向控制稳定性[2]。Fossen等先后研究了PID控制、最优控制、滑模变结构控制等航向控制算法[3]。Van Amerongen开发了直接模型参考自适应航向控制算法[4]。国内外船舶自动舵厂商先后开发了PID控制自动舵、自适应控制自动舵、最优控制自动舵和模糊控制自动舵等，但无论何种自动舵，均需要在海试中对控制器参数进行调整，以适应船舶的操纵特性和航行指标要求。

本文以航向运动自回归滑动平均模型（Autoregressive moving average model，ARMA）为基础，开展了模型参数辨识和最小方差自适应航向控制算法的研究，提出了船舶航向的最小方差间接自校正控制算法，期望获得一种不依赖船舶水动力数学模型，尽可能地减少船舶海试的控制器参数调试工作量。

1 船舶航向运动模型辨识

船舶航向偏差和舵角可用下述ARMA模型描述：

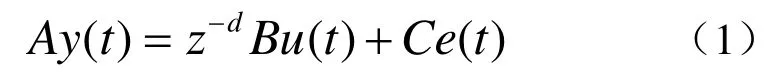
式中，

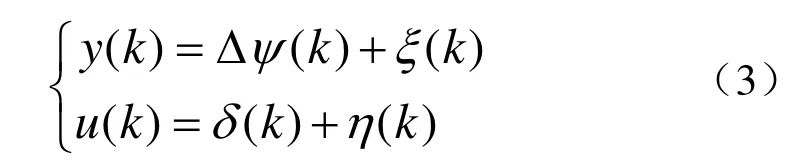
ξ(k)和η(k)分别是均值为 0、方差为和的不相关随机噪声，Δψ(k)和δ(k)分别为k时刻的航向偏差和实际舵角。

由K-T方程[3]可知，船舶航向偏差数学模型可转换为二阶ARMA模型，故可设na=2，nb=1，nc=1，式（1）可转换为

对上式整理后，可得

式（4）可转换为如下多项式方程：

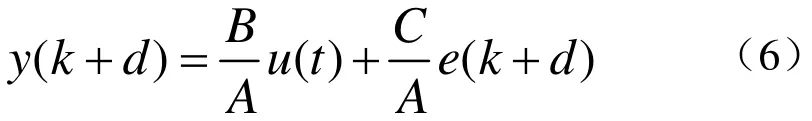
在初始辨识时，可采用逆M序列[5-6]作为舵机激励信号。其最小二乘格式为

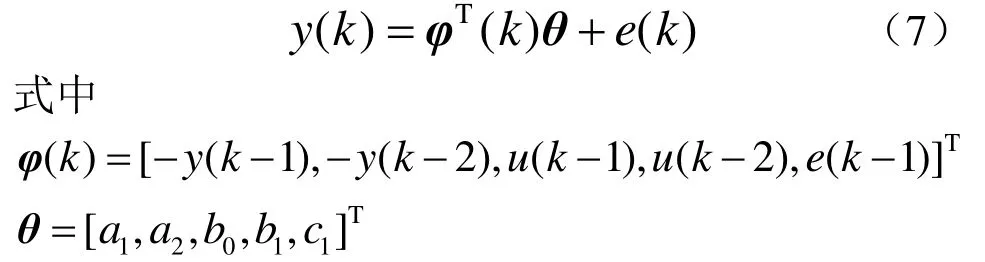
此时，噪声e(k)的均值为0，系统参数可采用随机牛顿算法进行估计。递推随机牛顿算法参数估计公式[7]为

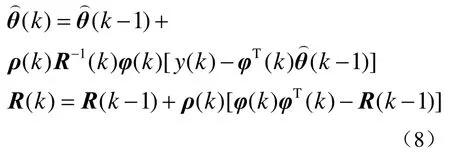
当式（8）中矩阵R(k)的2范数小于某一阈值时，则可认为模型参数具有很高的可信度，可停止模型辨识。

2 航向最小方差自校正控制算法

自校正最小方差控制算法基本思想是选择控制信号最小化输出方差：

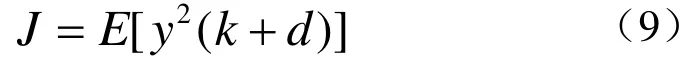
式中，d为延时。由式（4）可知，航向偏差ARMA模型中，d=1，则可定义多项式F和G分别为

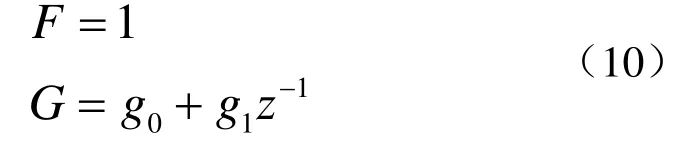
多项式F和G使得下式成立：

利用上述等式，由式（6）得

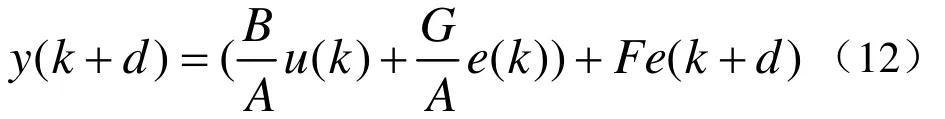
由式（4）可得

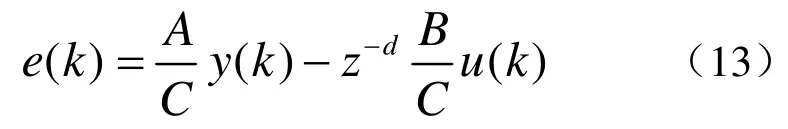
代入式（12），可得

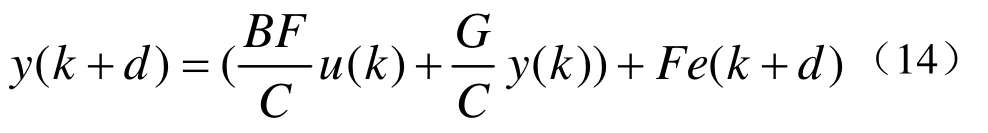
为了最小化输出方差，可选择控制信号u(k)使得

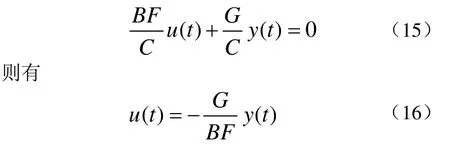
为了解式（16），将辨识得到的模型参数代入式（11），则可得

由于等式两边的系数相等，解得

将相应参数代入式（16），可解得控制律为

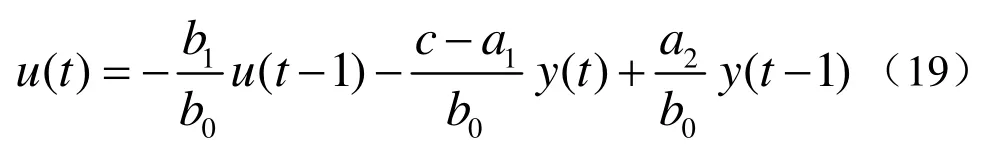
由航向最小方差自校正控制算法的设计过程可知，在控制律中，仅涉及到模型参数辨识的结果，而无须对控制律中任何参数进行调整，由此可知，该控制律会极大地简化设计过程，大幅缩减船舶试航周期，同时，船舶驾驶人员根据需要可在线实时进行模型参数的辨识，自适应调整控制规律，实现船舶的自适应航向控制。

3 仿真分析

3.1 基于逆M序列的模型参数辨识试验

为验证前述递归牛顿随机法参数辨识方法的正确性，利用文献[8]中船舶操纵运动建模方法和船舶参数，利用Matlab/Simulink仿真软件，建立了4自由度非线性数学模型，然后，利用逆M序列产生操舵激励信号对式（4）所示模型开展辨识仿真试验，参数辨识仿真条件为：

（1）逆M序列的采样时间为8 s；

（2）参数估计公式中，ρ(0)=5，R(0)=I5×5(0)为5行1列随机矩阵。

（3）船舶航行环境为深水，无风浪流干扰；

（4）初始航速15 kn，初始航向为60°。

仿真时间为500 s，仿真结果见图1～3。图4为辨识过程中矩阵R(k)的2范数变化曲线。

图1 辨识试验航向变化曲线

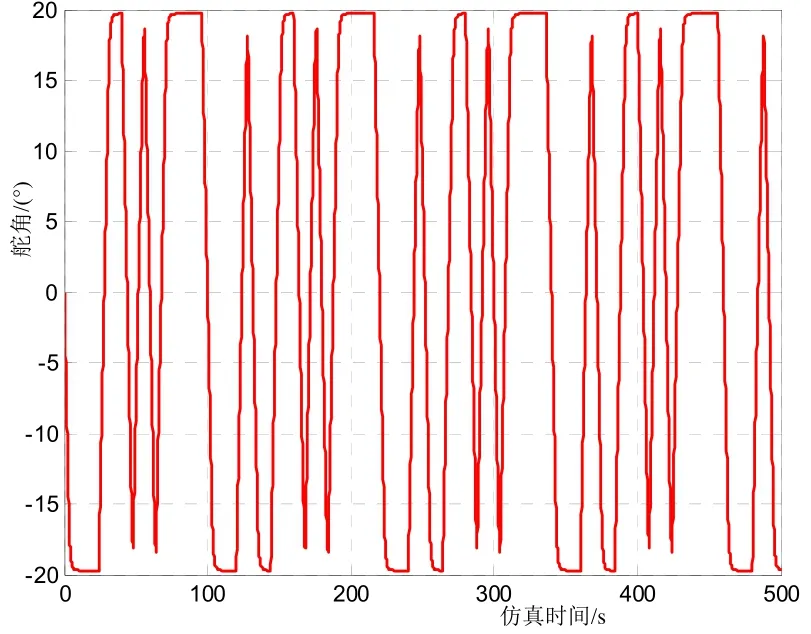
图2 辨识试验舵角变化曲线

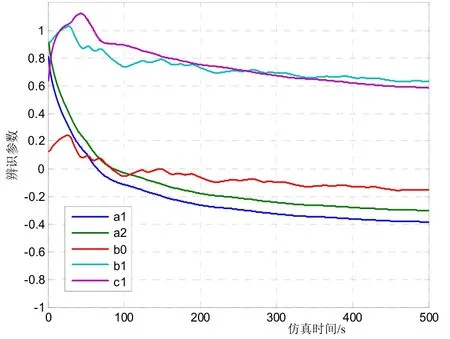
图3 辨识试验辨识参数变化曲线

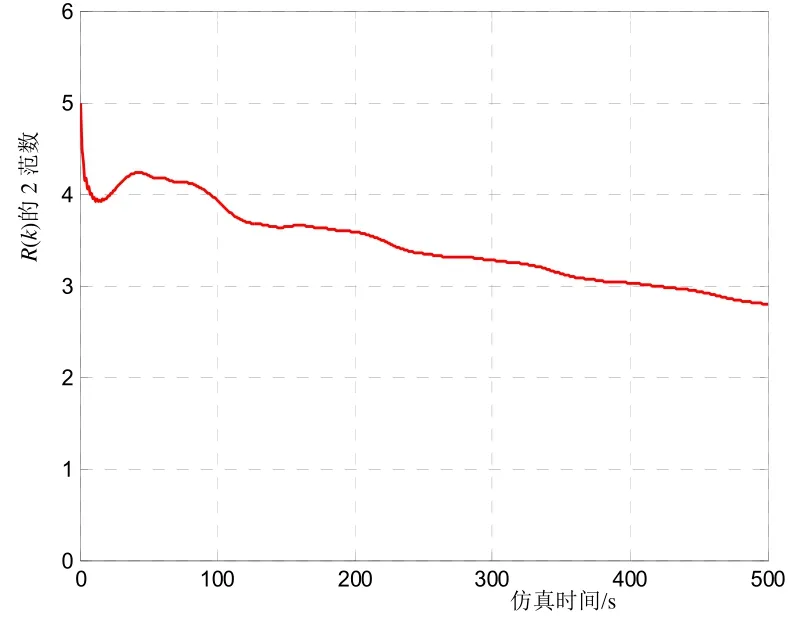
图4 辨识试验中R(k)的2范数变化曲线

结合图 3、4可以看出，模型参数随着辨识的推进逐渐收敛，R(k)的2范数随之逐渐减小，在300s后，各辨识参数的变化幅度已很小，R(k)的2范数也已减小到3以下，且减小速度愈发平缓。仿真结果表明，本文采用的模型辨识算法有效。

3.2 平静海况航向最小方差自校正控制仿真试验

在航向偏差模型辨识基础上，本文以上述15 kn下的辨识参数为初值，验证在22 kn航速下平静海况的航向最小方差自校正控制算法的控制品质。

初始航向设置为60°，指令航向设置为120°，模型参数辨识的停止阈值设置R(k)的2范数不大于3，仿真时间为500 s。仿真结果见图5～6，仿真过程中的模型辨识参数实时变化曲线见图7。

由图5可知，船舶在60°航向变化过程中，基本无超调、无振荡，调节时间为70 s，航向修正进入航向保持后，航向静态偏差为0.028 2°（RMS值），表明所设计的航向闭环控制系统为过阻尼控制系统，航向控制过程稳定，航向控制性能好。由图 6可知，在航向改变过程中，舵机运行平稳，可以最大舵角及时操纵船舶实现变向；在实际航向接近指令航向时段内，舵机可快速收舵，实现航向无超调无振荡；在航向保持过程中，船舶以极小的舵角实时控制航向，保证了船舶以极小的静态偏差直航。由图7可知，在航向修正过程中，仅有个别模型参数缓慢变化，表明所设计的控制律有较强的鲁棒性能。

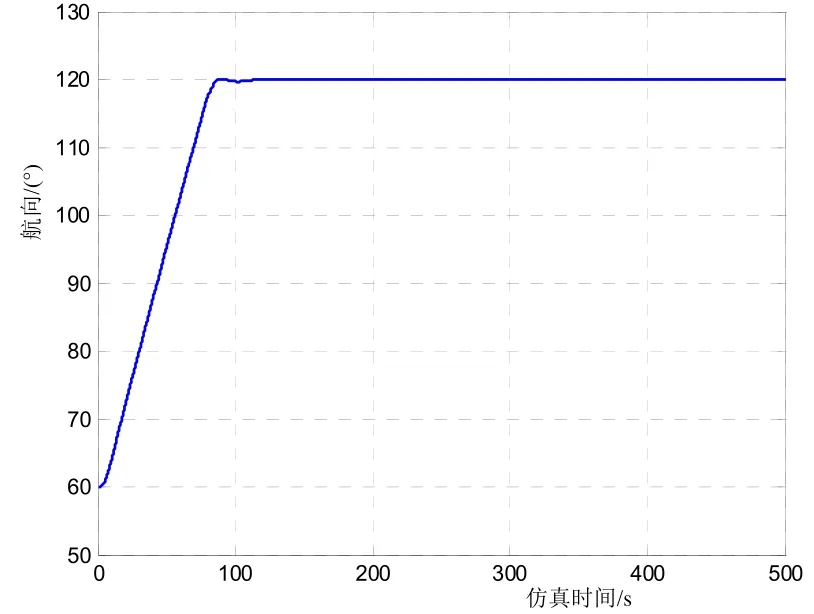
图 5 22 kn航速平静海况的航向变化曲线

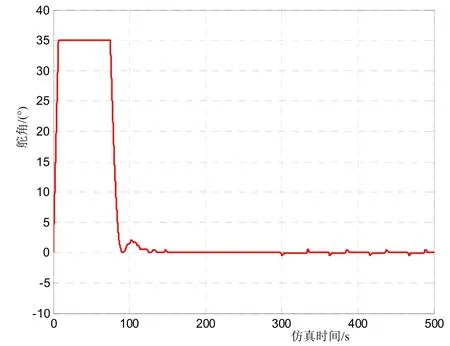
图6 22 kn航速平静海况的舵角变化曲线

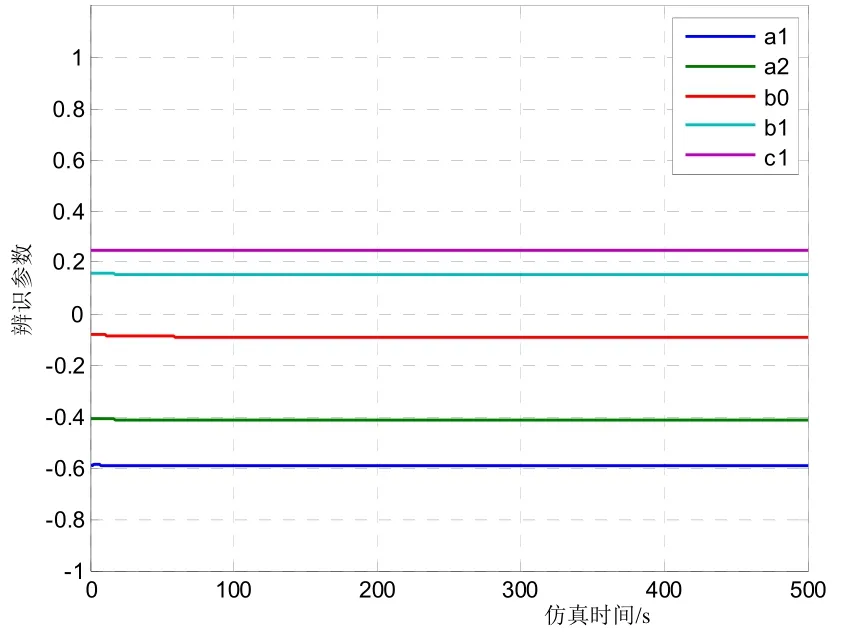
图 7 22 kn航速平静海况模型参数实时变化曲线

3.3 3级海况航向最小方差自校正控制仿真试验

为验证航向最小方差自校正控制算法在低海况海洋环境中的运动控制品质，仍以上述15 kn下的辨识参数为初值，仿真验证本文提出的算法在25 kn航速下在3级海况的控制品质。

仿真条件为：海况条件为浪向45°，浪级3级（H1/3ξ=1.25 m ），蒲福风级4级，风向45°；初始航向设置为-10°，指令航向设置为 60°，仿真时间仍为500 s。模型参数辨识的停止阈值同上。仿真结果见图8～9。仿真过程中的模型辨识参数实时变化曲线见图10。

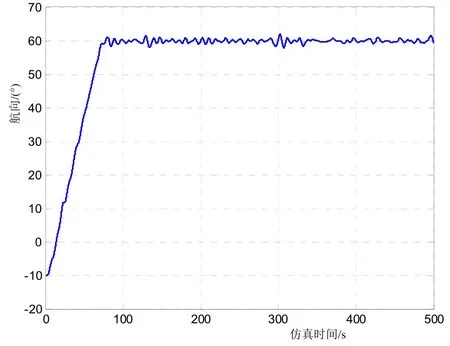
图8 25 kn航速3级海况的航向变化曲线

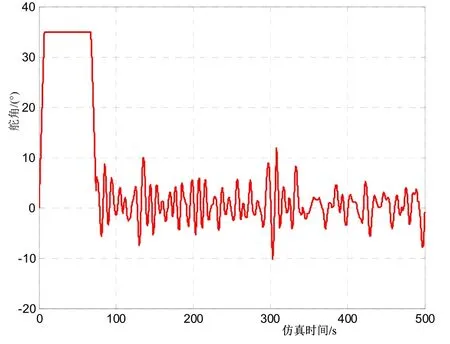
图9 25 kn航速3级海况的舵角变化曲线

由图8可知，船舶在70°的航向变化过程中，无超调，从初始航向到进入航向保持的时间为70 s左右，航向稳定偏差为0.587 3°（RMS值）。

结合图8～9可以看出，在航向修正过程的初始阶段，控制算法通过解算指令舵角后，激励舵机以满舵操纵，并保持满舵舵角直至实际航向接近指令航向；在航向修正到接近指令航向前，算法解算出快速收舵指令，激励舵机快速收舵，随后进入航向保持阶段；在航向保持阶段，由于风浪干扰，实际航向随着风浪变化而变化，最大航向偏差为2°，平均波动周期为10 s左右，基本与海浪周期相当。

由图 10可知，尽管海浪干扰对船舶航向产生了较大影响，但模型辨识算法依然可实现参数的平稳辨识，表明本文所应用的递推随机牛顿参数估计算法具有较强的自适应能力，辨识出的模型参数应用于最小方差自校正控制算法中，仍可得到较好的控制效果。

4 结论

本文针对实际工作中船舶航向控制律的设计需依赖精确的数学模型或需在船舶试航过程中耗费较多人力物力进行控制律调整的现状，提出了利用模型辨识方法得到初步的模型参数，进而利用最小方差自校正控制算法在线实时调整控制律参数的航向控制算法，完成了仿真案例验证。仿真过程中，利用15 kn航速下的模型参数作为初值，通过实时辨识参数调整控制律，验证了本文提出的最小方差间接自校正控制算法在平静海况和低海况下航向控制的有效性。仿真试验结果表明，本文提出的最小方差间接自校正控制算法具有良好的控制效果、控制品质，以及航速变化对航向运动特性影响的自适应能力，且不依赖水动力数学模型，工程实用价值较高。