利用FPGA实现的频率精估计方法

唐济远 袁春姗

（中国船舶集团公司七五〇试验场，昆明，650000）

对于水下探测设备来说，信号检测是难点，也是热门问题。水声环境复杂多变，多数情况下信噪比条件恶劣，频率估计精度差，但实时性要求又较高。如何在工程实践中精确估计未知信号的频率信息，是工程设计人员不断面临的挑战。

在不同的信噪比条件下，不同方法所得到的频率估计精度各不相同，但是，无论采用哪种频率估计方法，其频率估计的均方根误差（Root Mean Square Error，RMSE）都不会小于克拉美-罗界[1]（Cramer-Rao bound，CLRB）。

文献[2]给出了基于Rife算法的频率估计方法，在对输入信号进行一次FFT运算后，利用最大谱线及其左边或右边的一根次大谱线进行插值来确定真实频率位置。该算法只需要一次FFT运算，运算量小，容易硬件实现。Rife方法在量化频率中心区域的频率估计误差很小，但是在量化频率点附近的误差却较大。而修正Rife算法通过对输入信号进行频谱搬移，使得信号的频率始终位于量化频率的中心区域，提高了频率估计精度。

同时，FPGA的并行性好，文献[3]介绍了利用FPGA实现修正 Rife方法的设计思路。本文利用XILINX公司的FFT核[4]，将修正Rife方法在FPGA中进行了硬件实现。FPGA布局布线后的时序仿真表明，本文设计实现了对采样率为200 kHz信号的实时频率估计功能。

1 方法介绍

1.1 Rife方法介绍

当输入信号的频率不在FFT量化频率点处时，直接用 FFT运算的最大谱线位置来估计正弦输入信号的频率，存在量化误差，其误差范围为[-fs/2N，fs/2N]（fs为采样频率，N为FFT点数）。Rife方法利用最大谱线以及与其相邻的次大谱线进行插值估计信号频率。设在高斯白噪声环境下的正弦波信号为

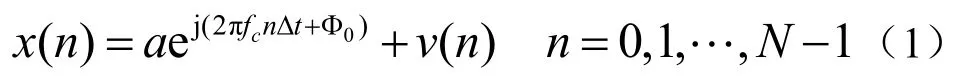
式中，a、fc、Φ0分别为振幅、频率和初相，Δt为采样间隔，N为样本数。v(t)是实部和虚部相互独立的、方差为2σ2的零均值高斯白噪声（实部、虚部都服从N(0,σ2)分布）。对x(n)作FFT，最大谱线值记为|X(k0)|，次大谱线值记为。则Rife算法所得到的频率估计值[1]为

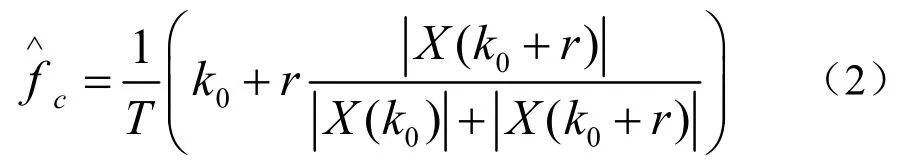
图1 Rife方法示意图

文献[1]证明当输入噪声为零时，Rife算法能够得到精确的频率估计结果。在适当的信噪比条件下，当fc位于两个离散频率的中心区域时，Rife算法性能较好，其频率估计均方根误差接近CLRB，误差远小于 FFT算法；反之，当信噪比较低而且fc接近量化频率点时，误差甚至大于FFT算法。这是因为当fc位于离散频率中心区域时，|X(k0+r)|与|X(k0)|很接近，这时采用式（2）的内插公式具有较高的精度；但是，当fc接近于量化频率点时，则|X(k0+r)|与|X(k0)|差别很大，|X(k0+r)|很小，在噪声的影响下，将产生频率插值的方向性错误，因此频率估计精度降低。

1.2 修正Rife方法及实现步骤

将Rife方法的频率插值记为δ1，有[2]

则有δ1∈[0,1/2]。当δ1∈[1/3,1/2]时，Rife 算法精度很高；当δ1∈[0,1/3]时，估计能力下降。定义δ1∈[1/3,1/2]为量化频率中心区域，当由Rife得到的频率估计结果位于此中心区域时，将其作为最终输出；否则，将信号频移r/3倍量化频率。信号频移采用与复指数相乘，从而实现信号单方向的频移。平移后的信号为

由于是固定平移r/3倍量化频率，所以复指数的计算可通过查表来实现，减少了计算量。对平移后的信号再应用 Rife算法进行频率估计，若所得δ1∈[1/3,1/2]则将此时估计出的频率减去r/3倍量化频率，即为最终的频率估计结果；若所得δ1∈[0,1/3]，则说明频率移动方向错误，将式（4）中的r取反，再使用Rife方法进行频率估计，将所得结果减去r/3倍量化频率，即为最终的频率估计结果。其运算步骤如下：

（1）对输入信号x(n)做FFT运算；

（2）计算δ1，当δ1∈[1/3,1/2]，则用式（2）定义的Rife方法进行频率估计，结束运算。

（3）当δ1∈[0,1/3]，用式（4）对信号进行平移，对平移后的信号做 FFT，重新计算δ1，若δ1∈[1/3,1/2]，用式（2）估计频率，并将其减去r/3倍量化频率作为最终频率估计值，结束运算。

（4）当重新计算的δ1∈[0,1/3]，则将r取反，返回第三步。

通过对原始信号的频移，保证了δ1∈[1/3,1/2]，充分发挥了Rife算法在量化频率中心区域精度高的优势，使得频率估计精度大为改善。

2 FPGA实现方法

2.1 系统设计

根据1.2节给出的修正Rife方法，在FPGA中完成硬件实现。硬件设计中为了充分发挥FPGA并行运算的优势，提高运算速度，提高修正Rife方法的实时性，将输入信号分成并行的3路，第2路左向频移-1/3量化频率间隔，第3路右向频移1/3量化频率间隔，第1路保持原始信号不变。每路中采用一个FFT模块对各路信号进行FFT运算。采用1.2节介绍的方法计算3路通道修正量选取其中最接近1/2的值作为有效频率估计通道。如果有效频率估计通道为第2路，则最终修正量为；如果有效频率估计通道为第3路，则最终修正量为；如果有效频率估计通道为第1路，则最终修正量为。根据最终修正量，结合式（2），对信号真实频率进行估计。设计中采用XILINX公司Artix系列FPGA器件中的XC7A100T2FTG256芯片[4]，在ISE14.7中进行编程、综合、布局布线和时序仿真。所得设计的RTL图如图2所示。

图2 修正Rife方法FPGA实现RTL图

系统设计主要由3个FFT模块、3个Rife模块、2个ROM模块和一个判决模块组成。3个FFT模块用来完成3路并行的FFT运算；Rife模块用来实现Rife方法以及修正量的计算；2个ROM模块用来存放频移所需复指数的实部和虚部。对于采样频率固定、FFT分析点数固定的系统来说，频移系数为两个固定反向的复指数，两个ROM模块由于在固定的信号通路上，所以与固定指数相乘即可。判决模块对 3路并行计算的结果进行判决，选取最大值，并相应的加减频率，给出最终的频率分析结果。FFT模块可通过XILINX公司FFT核的参数来完成设计，其他模块采用VHDL硬件描述语言来实现。

2.2 硬件设计资源消耗分析

在ISE14.7软件中建立工程，经综合、布局布线后的资源使用情况如表 1所示。采用XC7A100T2FTG256芯片能够在一片 FPGA内实现并行结构的修正Rife方法。这种并行、流水的处理方式，加快了处理速度，提高了系统的实时性，适合在水声信号检测、水声探测、水声诱饵等信噪比较低、系统实现性要求高的领域应用。该设计的缺点是消耗的逻辑单元和DSP模块比较多。

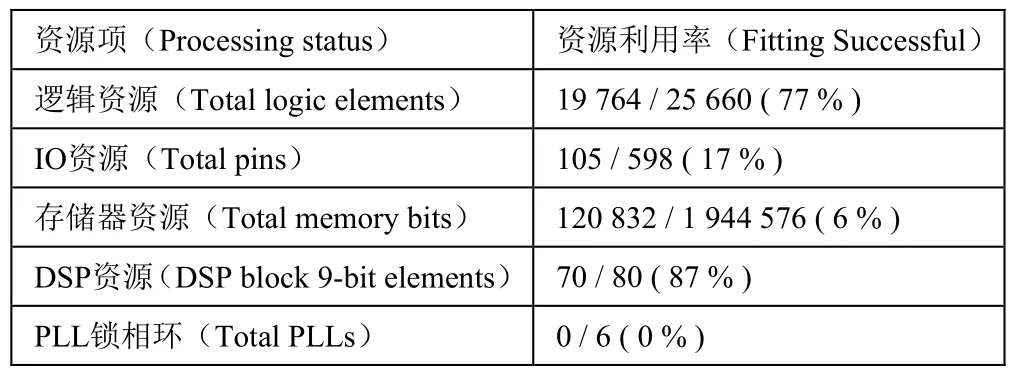
表1 FPGA主要资源消耗表

2.3 设计后仿真

将设计在 Modelsim软件中进行布线布局，得到设计的延迟模型，再用Matlab软件生成仿真所需的向量文件（*.vec文件）。系统输入两段频率分别为（65.15/N）×fs和（110.5/N）×fs的信号，长度都为256，信噪比SNR=-3 dB。data_real_in表示输入信号，位宽16 bit。系统时钟信号为clk，复位信号为reset。系统输出信号为k0、r和deta，其中k0和r的含义与式（2）中的一致，r的高、低电平代表取正、取负。deta为Rife算法的最终修正量，位宽为16 bit，用来表示16位无符号定点小数。当修正量为1时对应deta值为65 535。修正Rife方法的时序仿真波形如图3所示，局部信息放大如图4所示。根据图中显示，第一段信号k0=65、r=+1、date=8782，则实际估计的频率k0+r×deta/65 535=65.134, 单位是1/N×fs；第二段信号k0=111、r=-1、date=30 867，则实际估计的频率为k0+r×deta/65 535=110.529, 单位是 1/N×fs。时序仿真表明，设计最高运行速度可满足采样率200 kHz信号的处理要求，数据无延迟，能够实现并行、流水、实时处理，可以较为准确的估计真实信号频率。

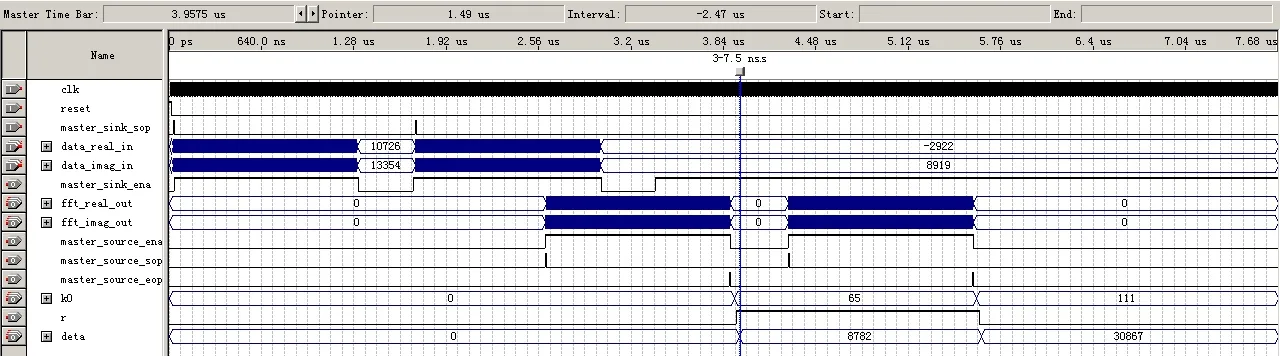
图3 修正Rife方法FPGA仿真图

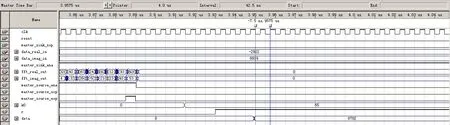
图4 修正Rife方法FPGA仿真细节图

3 小结

本文分析了原始Rife方法和修正Rife方法各自的优缺点，说明了修正Rife方法在量化频率点附近对频率估计精度的提高效果。对修正Rife方法在FPGA中的硬件设计方法进行详细介绍。充分利用了FPGA器件的优势结构，对修正Rife方法进行并行运算设计。最后，给出了FPGA资源消耗情况以及后仿真结果。该设计方法可以应用于多种水下信号检测设备中，在低信噪比的水声环境、实时性要求高的水声检测系统中有较好频率估计效果。