一类分数阶差分方程非局部边值问题解的存在唯一性 ①
吴 颖, 王良龙
(安徽大学数学科学学院,安徽 合肥 230601)
0 引 言
1965年, 著名数学家Leibniz和Hospital进行了有意义的通信, 在通信中谈及了分数阶导数以及分数阶微分[1]. 出于理论发展和应用需要, 分数阶微分方程获得极大发展, 其中Riemann-Liouville型分数阶微分方程更是引起了各界广泛关注, 研究结果层出不穷[2,3].
众所周知, 如同整数阶微分方程, 对一般的分数阶微分方程也很难获得其解的表达式或精确表示. 出于研究的需要, 当把分数阶微分方程离散化时便得到相应的分数阶差分方程.分数阶差分、分数阶和分以及分数阶差分方程理论的研究均具有很大的挑战性, 所以吸引了许多中外学者的关注. 另一方面, 分数阶差分方程能很好地刻画实际模型, 在材料科学, 医药科学, 生态数学模型上的研究中有着重要应用[4-6].
目前很多学者在分数阶差分方程方向做出了的一些结果,其中绝大部分研究了阶数在1-2之间的分数阶差分方程,还有一小部分攻克了阶数在3-4之间的分数阶差分方程,在合适的条件下均获得了不错的结果[7,8].本文在前人的基础上考虑了一类任意阶的分数阶差分方程的非局部边值问题,运用了Banach不动点定理, Brouwer不动点定理在合适的条件下得出该分数阶差分方程非局部边值问题解的存在唯一性.
1 预备知识
本节给出若干记号, 定义和预备引理[6,8].
函数y(t)的一阶差分记为Δy(t)=y(t+1)-y(t). 设N,b是非负整数,v∈R, 记
Nv={v,v+1,…},
Nv-N,v+b={v-N,v-N+1,…,v+b}.
考虑如下一般形式分数阶差分方程的非局部边值问题
(1)
其中N-1 定义1.2若v>0, 函数y(t)的v-阶和分定义为 函数y(t)的v-差分定义为 Δvy(t)=ΔNΔ-(N-v)y(t),t∈Nv-N,v+b, 其中N是非负整数, 满足N-1 引理1.1令0 其中ci∈R, 1iN. 引理1.3分数阶差分、分数阶和分运算具有下列性质: (1)令u>0,v>0, 有Δ-vΔ-uy(t)=Δ-(u+v)y(t). (2)令N是满足N-1 引理1.4记Y={y:Nv-N,v+b→R},f:Nv-N,v+b×R→R是连续函数,g:Y→R是一个连续泛函, 则函数y(t)是分数阶差分方程非局部边值问题(1)的解, 当且仅当y(t)满足 (2) 其中t∈Nv-N,v+b,N是满足N-1 证明:充分性: 由引理1.1可得 (3) 且 由(1)知 y(v+b)=-Δ-vf(t,y(t))|t=v+b+ (4) 由上式(4)解得 所以 充分性得证. 必要性显然成立就不在此赘述了, 综上, 引理1.4得证. Y如前所定义, 对任意的y∈Y, 定义‖y‖=max{|y(t)|:t∈Nv-N,v+b}, 则(Y,‖·‖)是一个Banach空间,定义算子T:Y→Y, 其中 (5) 定理2.1假设f(t,y)和g(y)对y满足Lipschitz条件, 即存在α>0,β>0使得 |f(t,z1)-f(t,z2)|α|z1-z2|, t∈Nv-N,v+b,z1,z2∈R, |g(y1)-g(y2)|β‖y1-y2‖,y1,y2∈Y, 若 (6) 则非局部边值问题(1)存在唯一解. 证明:只要证明T:Y→Y是一个压缩映射, 对任意给定的y1,y2 ‖Ty1-Ty2‖α‖y1-y2‖× (7) 由引理1.2知 (8) 且 α‖y1-y2‖× (9) 由引理1.2(5)得 (10) 综上得 ‖Ty1-Ty2‖ 则T:Y→Y是一个压缩映射, 由Banach压缩映射原理知边值问题(1)的解存在唯一. 定理2.2假设存在常数M>0使得f(t,z)和g(y)满足下列条件 证:令Y0={y∈Y:‖y‖M},则Y0是Y的有界凸闭集. 记 则ω0是严格正常数,由定理2.1知 ‖Ty‖+ 因此,T:β→β, 又f(t,y(t)),g(y)均连续, 易知T为连续算子, 由Brouwer不动点定理存在T, 使得Ty0=y0,y0∈β,y0是边值问题(1)的解,y0满足|y0(t)|M. 利用压缩映射原理和Brouwer不动点定理在合适的条件下讨论了一类阶数任意的分数阶差分方程非局部边值问题解的唯一性与存在性,实际上还可以继续研究该问题的正解的存在性.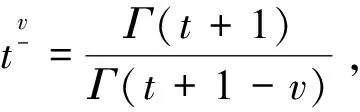
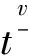


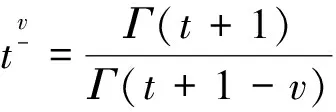

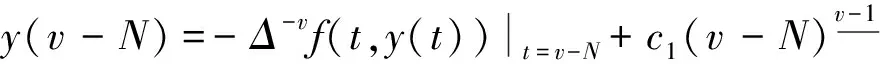
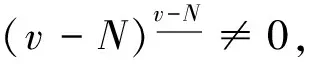
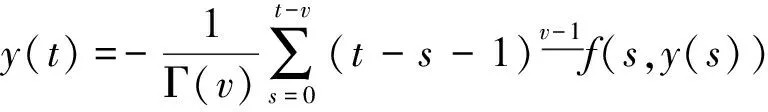
2 解的存在唯一性

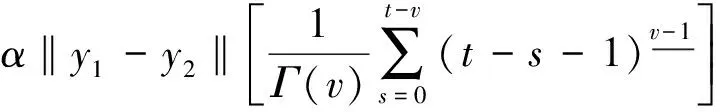
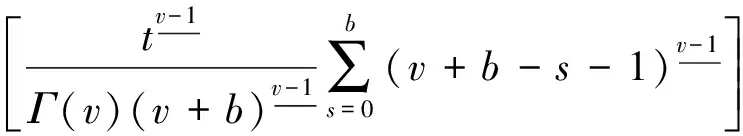
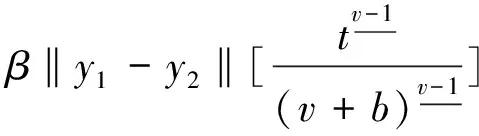
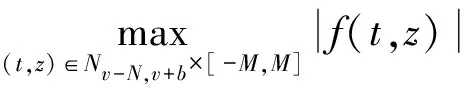
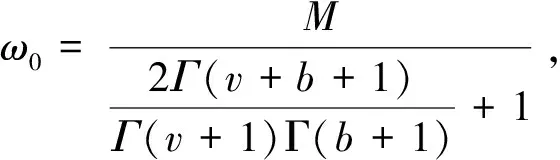
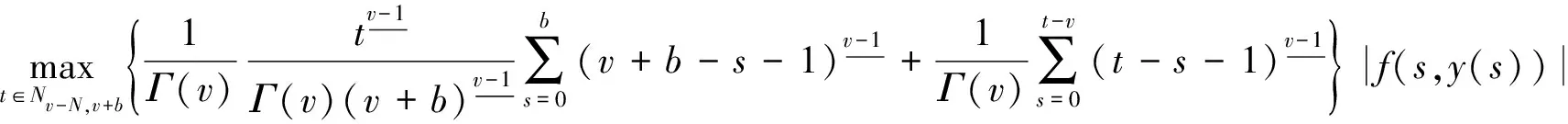
3 结 语

