考虑日周期性的城市电力负荷短期自回归预测

李 强，李 玮，吴开宇，秦知航，高 璐

(1.国网武汉供电公司，湖北 武汉 430000; 2.北京国网信通埃森哲信息技术有限公司，北京 100100)

随着电力体制改革的逐步深入，我国的售电市场获得了进一步开放。同时，可再生能源的发展，综合能源业务的开展，泛在电力物联网的提出，使得电力用户的负荷预测在能源管理的过程中的作用也越发的丰富和深入。通过对集体用户的短期负荷预测，政府和电力调度部门可以对城市不同区域的能源利用进行合理配置，以提高能源利用效率；能源管理部门可以针对园区、综合体等集体用户进行合理的能源规划，以降低发电以及旋转备用的成本；售电公司可以针对不同用电特征的用户提供定制的精细化售电服务套餐，降低用户成本，并提供贴心的供电服务，提升客户满意度与用户粘度。

电力用户的用电行为受到多种因素的影响，由于用户情况复杂，配电系统的运行状态存在差异，电力用户的用电数据一直存在数据获取的难度大，数据量大等问题。近年来，随着智能电表、计算机技术以及大数据的发展，使得用电数据获取的精度、信息量都有了较大提升，为用户用电行为的精细化分析提供了新的机遇。

负荷预测按照预测期限的不同，分为长期预测、中期预测、短期预测、超短期预测，分别对应年度预测、月度预测、日预测、小时预测。某些地区的预测还包括旬预测、星期预测。根据预测机理的不同，又将年度预测、月度预测合称为中长期预测，日预测、小时预测归为短期预测[1]。现有的预测方法主要分为传统方法和智能方法两大类。传统方法包括时间序列法、卡尔曼滤波预测法、灰色预测法等；常用的智能方法包括：神经网络法、支持向量机预测方法、混沌预测法和小波分析法等[2]。其中，传统的预测方法基于数据本身的变化规律，进行数值分析和预测。而智能方法通过智能算法对历史数据规律进行学习，在学习的基础上进行预测。

在数据预测方面，国内的研究主要集中于预测理论应用与预测模型调整。其中，文献[3-4]从风电电源以及空调负荷的角度为预测模型的建立提供了参考；文献[5-7]阐述了自回归预测的理论，并结合各自的模型进行了应用；文献[8]在负荷预测过程中，对负荷的周周期性进行了应用；文献[9]采用向量回归机回归模型对车辆排气噪声品质进行了预测，获得了更接近实测值预测值。

国外的研究主要集中在新技术集合以及预测模型建立方面。其中，文献[10]对商业建筑电力负荷预测回归分析和机器学习技术进行了分析与总结。文献[11]运用天气、占用率和时序数据对瑞典办公楼的电力负荷进行了日前预测，并取得了良好的预测效果。文献[12]建立了一种混合神经网络对风电功率进行了日前预测，获得了比传统方法更好的预测效果。

对于城市集体负荷，由于数据量大，对计算的要求较高。为提高预测效率，寻找更为高效的预测方式，本文采用传统预测方法中的自回归预测的方法，从单月的用电数据出发，通过数据本身的变化规律进行日负荷预测。

1 电力负荷的日周期性

1.1 单个用户电力负荷的日周期性

某典型用户的月内电力负荷曲线如图1所示，由图中可以看到，该用户的电力负荷曲线呈现较为规律的周期性波动。

图1 某典型用户的月内电力负荷曲线

将该用户月内共28天的日用电负荷曲线按照叠加在同一天内，得到图2所示的月内日电力负荷叠加曲线。由图2可以看到，该用户的日内电力负荷曲线呈现重合的趋势。用户的日内用电负荷曲线一定程度上可以反映出用户的用电习惯。

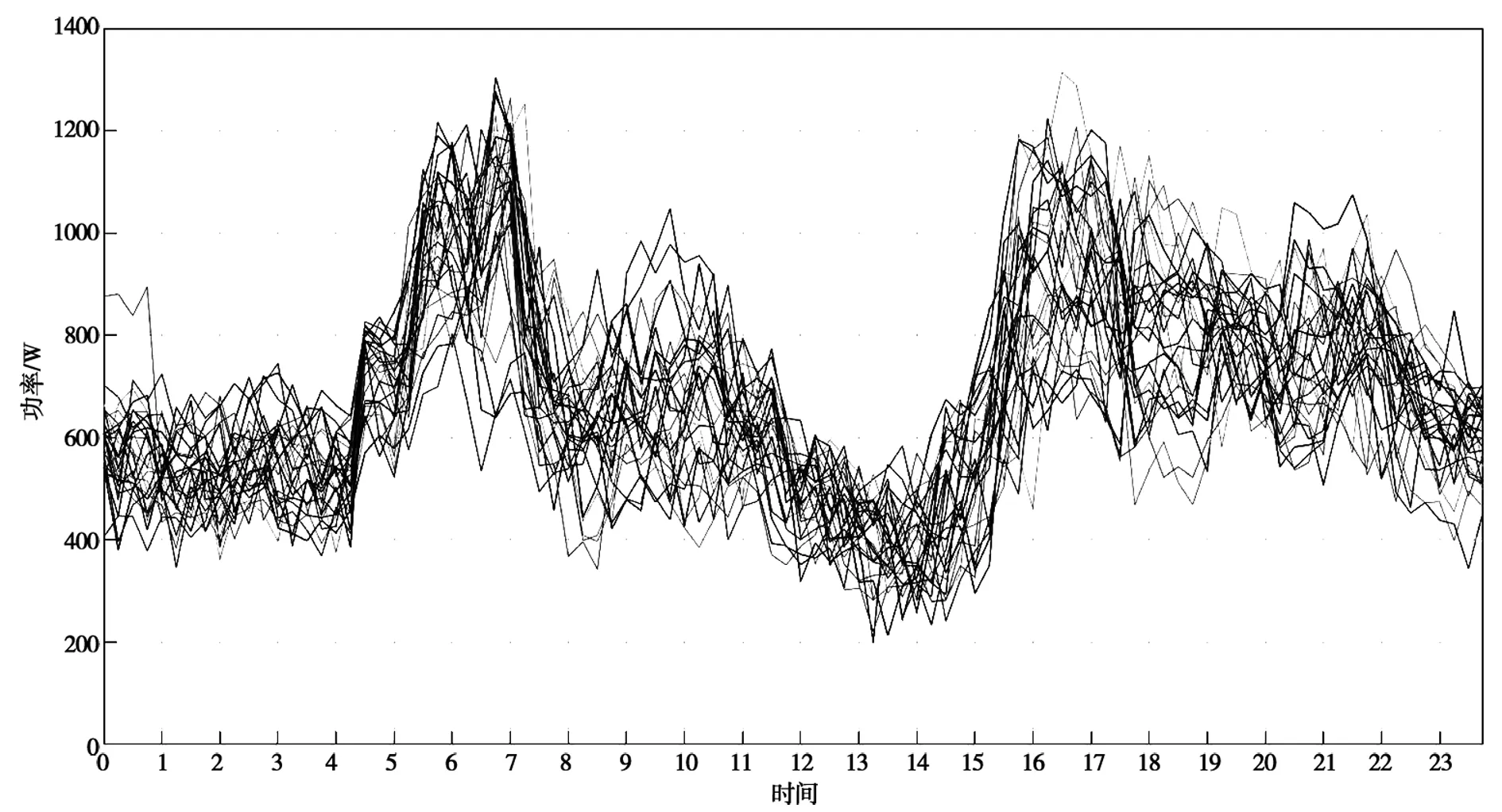
图2 某典型用户的月内日电力负荷叠加曲线

1.2 集体用户电力负荷的日周期性

北方某城市18 435个电力用户的集体月内电力负荷曲线如图3所示。由图中可以看到，随着用户数量的增多，用户的集体电力负荷呈现更加平稳的周期性波动。受春节影响，2月1日到7日负荷曲线峰值偏高，且波动较为明显，节后负荷曲线逐步趋于平稳。

图3 北方某城市18 435个电力用户的集体月内电力负荷曲线

将18 435个用户28天的负荷曲线叠加绘制在同一天内，如图4所示，可以看到，集体用户28天的负荷曲线模式较为相似，由于春节的影响，部分曲线偏离稍大，但总体曲线的波动方式与幅值均在相近的范围之内。

图4 18 435个电力用户的集体月内电力负荷叠加曲线

总体来说，受用户用电行为习惯等因素的影响，单个用户和集体用户的用电负荷曲线按日呈现周期性波动，相对于单个用户来说，集体用户的周期性波动更加平稳。

1.3 自回归预测模型

自回归模型(Autoregressive Model，AR)用自身做回归变量的过程，即利用时间序列x1,x2,…xn-1时刻值进行线性组合，来预测xn的表现。

对一个时间序列x1,x2,…xn，p阶自回归模型表明序列中的xn是前n-1个序列的线性组合以及误差项的函数，一般形式的数学模型为

式中k0——常数项;

ki——模型参数。

2 城市集体用户的自回归预测

2.1 研究框架

本文的研究总体分为3个部分，整体研究框架如图5所示。首先，收集了中国北方地区某城市春季(2019年2月)一个月共28天的用电数据。

图5 整体研究框架

由于表计的差异与现场情况的差别，获取的数据首先需要经过处理，去除包含数据缺失和不正常的用户数据，筛选出满足条件的集体用户负荷共18 435户，并将18 435个用户的电力负荷曲线加总，形成该城市集体负荷曲线。接下来，采用多元自回归预测的方法，以前27天的负荷数据作为基础，对第28天的负荷曲线进行预测，得到城市集体负荷预测曲线。最后，将预测曲线与实测的用户用电曲线进行比对，并对预测的误差进行了评估。

2.2 数据的获取与处理

本文获取的数据为北方某城市的电力计量数据，原始数据以tab间隔，以txt格式存储，电流和电压文件分别为单独的txt文件，数据间隔为15 min，每天的电力负荷数据包含96个点，共28天的历史数据。

通过对原始数据的分析发现，获取的数据存在以下问题：

(1)数据缺失：部分用户的电力负荷数据存在不同程度的缺失，日电流、电压曲线不完整。

(2)数据错误：部分用户的电流、电压数据出现了负值的情况。

在数据的处理方面，本文首先对数据进行了清洗，日电流、电压数据点数不足96个点与电流、电压出现负值的用户数据；接下来，通过对应日期、用户编号将用户的电流、电压一一对应，得到用户的功率曲线；最后，将筛选出的18435个用户的功率曲线叠加，形成集体用户的功率曲线，如图3所示。

2.3 多元自回归预测

城市集体用户的每天的负荷曲线包含m个点，共n天的基础数据，其中第i天的负荷曲线可以表示为

预测的基础数据共n天，其负荷曲线可以表示为

待预测的第n+1天负荷数据为

本文共获取了28天的历史用电负荷数据，对于第1到27天

通过最小二乘法，由第1到27天的数据，可以获取到回归系数k0…k26，再由

即可获取到第28天的用电负荷预测值。

2.4 误差分析

对于预测的误差分析，文献[10]通过正规化方均根差与方均根差2种方法计算预测误差。由于城市集体负荷的用电数据数值较大，为更好得反应预测曲线与实测曲线之间的偏差情况，本文选用正规化方均根差(NRMSE)，对预测的误差进行了分析。其计算方法如下

式中yt——t时刻的实测值;

3 预测结果分析

本文的预测结果如图5所示，其中预测曲线为蓝色虚线，实测曲线为红色实线。由图中可以看到，预测曲线可以较好地跟随实测曲线的波动。通过计算，预测曲线与实测曲线的正规化方均根差(NRMSE)为0.014 8，处于较小的误差范围。

图6 短期自回归预测结果

4 结论

(1)对城市个体以及集体负荷的日周期性波动进行了分析，由于用户用电行为习惯等因素的影响，用户的个体和集体用电曲线在一定程度上都呈现以日为周期的波动，其中集体用户的周期性更为明显。

(2)针对城市集体电力负荷的日周期性，设计了以月用电数据为基础的自回归预测方法，可通过月内已知的用电数据对日用电曲线进行预测。

(3)采用实测数据对北方某城市18 435个用户的集体负荷进行了数据处理和预测。通过对比，预测曲线与实测曲线吻合程度较高，且预测的正规化方均根差较小。

(4)预测基本数据量的限制目前还有待探讨，即如何使用最少的基础预测数据达到较好的预测效果。

(5)节假日及周末对预测的影响有待后续研究。