“玻璃碎片的折射率测量”的STEM课程尝试
顾 琦
(无锡市第一中学,江苏 无锡 214000)
一直以来,物理课大多是以“客观规律学习→实验验证或测量→习题应用(显性的习题练习)”,或者是“实验探究下规律的学习→实例应用(隐形的习题练习)”的面貌出现在教师和学生面前的.是否还可以做些新的尝试呢?
1 高中物理核心素养对学生认识科技的应用提出了要求
利用玻璃砖“测定玻璃的折射率”,是学生在学习了折射定律后开展的实验.常规教材中的安排就属于“客观规律学习→实验验证或测量”这一类型.
无论是学生实验中采用的插针法,还是教师课堂演示实验中激光束的显示,都是为了获得光路,之后确定界面和法线,就可以找到折射角和入射角,然后运用折射定律求出折射率.
那么,在实际生产生活中,折射率真的都是这样测定的吗?高中物理核心素养的提出,比以往更关注了物理规律在实际生产、生活中的应用.那么这个问题也就值得深究了.
2 STEM课程为学生认识“从‘学科规律’到 ‘科学技术’的转化”提供了可能
STEM课程《福尔摩斯探案之玻璃碎片的折射率分析》以一起凶杀案为背景,从法医鉴定的角度出发,研究凶案现场的玻璃碎片与嫌疑车辆破碎大灯玻璃之间的关系,从而确定或者排除嫌疑车辆.基于学生的学科基础,以比对玻璃折射率为手段进行研究.
“可以直接运用折射定律来测定碎玻璃的折射率吗?”当笔者把这个问题抛给学生时,学生立刻提出了反对意见:“碎片太小”、“不易找到平整的两个表面”、“即使玻璃片有平整表面,但厚度太小”.
的确,学生提出的情形,以及测量精度不高,都是实际测量中会遇到的不理想情况.
毕竟学科规律并不等同于科学技术,两者之间还有很大的一步跨度.STEM课程将“科学、技术、工程、数学”等学科综合应用,所以,STEM课程就是让学生来认识“学科规律→科学技术”这样一个大跨度“桥梁”的.
3 跨学科的STEM课程也向教师打开了学习之窗
STEM课程《福尔摩斯探案之玻璃碎片的折射率分析》提供的是观察贝克线的方法.
什么是贝克线,其中有什么规律,物理原理又是什么,还有如何让学生来理解其中的转化过程?这门STEM课程,从一入手就体现出了不低的要求:物理教师自己先要身体力行的践行“发现问题、分析问题,解决问题”的过程.
经过网络检索和资料查阅,笔者发现:“贝克线”由德国学者贝克最早发现,主要运用在矿物、岩石、矿床及地球化学等专业的研究中.在显微镜下,升降物台或镜筒,贝克线会相对边缘平行移动.具体为:下降物台(或提升镜筒),贝克线相对边缘向折射率大的介质一方移动;提升物台(或下降镜筒),贝克线相对边缘向折射率小的介质一方移动.
测量方法是这样的:在显微镜下观察特定液体中玻璃粉末边缘贝克线的移动情况,就可以判断玻璃与该液体折射率的大小关系,更换不同折射率的液体(在实际玻璃折射率测量系统中则是通过改变液体温度来调整液体折射率),从而不断逼近玻璃折射率的准确值.当玻璃折射率与液体折射率相同时,贝克线就会消失.根据资料说明,该方法在白光下灵敏度可达0.001,单色光下可高达0.0005.精确度远高于平时课堂中玻璃砖的测量结果啊!
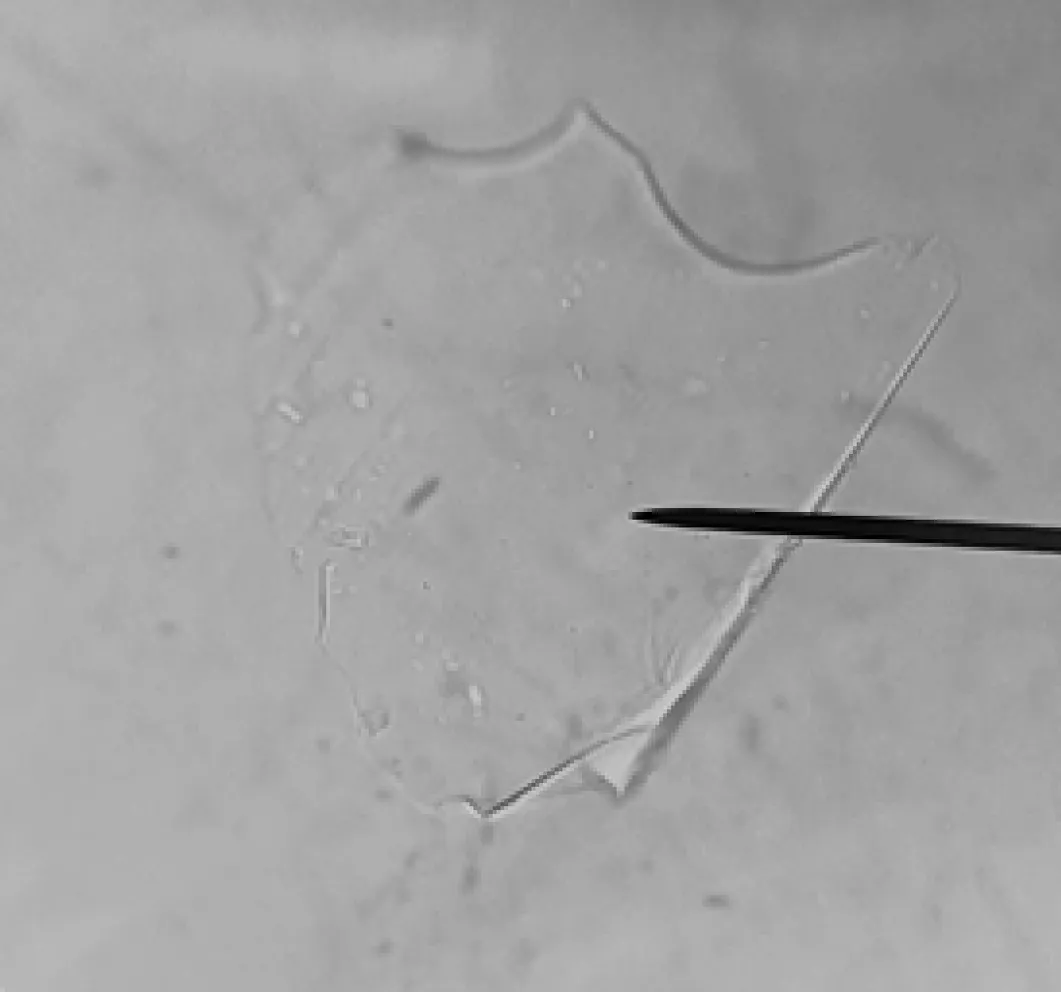
图1 显微镜下的玻璃碎片
不过,光看这些结论和书籍上的分析,都只能是纸上谈兵,从理解内容到能据此合理组织课堂教学还是存在不小的差距,所以还得亲自动手实践.借来显微镜,在载玻片上用牙签挑少许材料包里“已知车辆的前照灯”的玻璃粉末、再滴上折射率为1.45的液体、盖好盖玻片制成玻片标本,放到载物台上,选择10倍物镜,粗调、微调,在视野中找到一个比较明显的玻璃碎片,如图1.碎片边缘的亮线就是“贝克线”,而边缘上的黑线就是“边界”,此时合焦,两者几乎重合了.提升、下降镜筒果然看到亮线会移动:当镜筒上升时,如图2可以看到亮线(贝克线)往玻璃碎片内侧移动(出现失焦模糊也是正常情况);而镜筒下降时,贝克线会往玻璃碎片外侧方向移动,甚至移动到了边界黑线外侧,如图3所示.
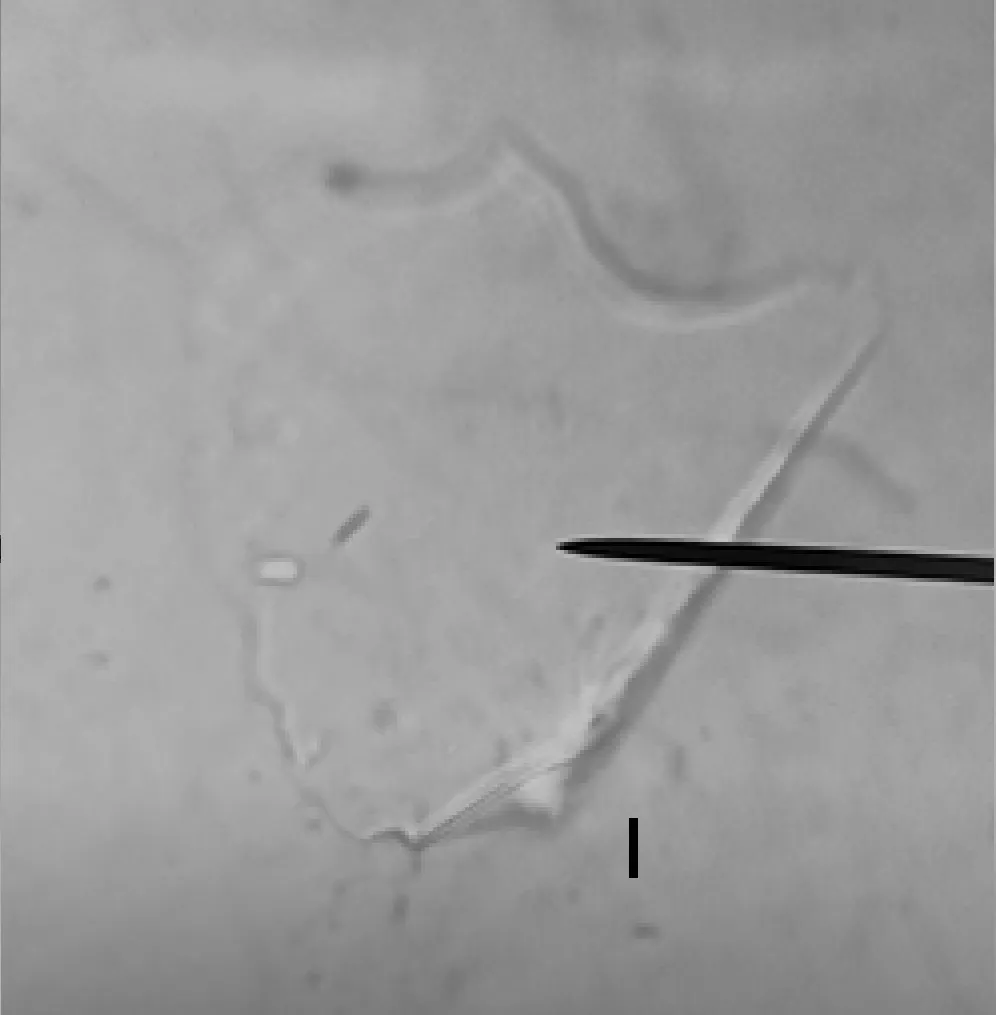
图2 贝克线向玻璃片内侧移动
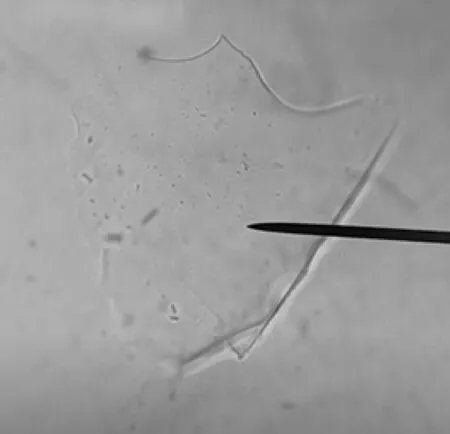
图3 贝克线向玻璃碎片外侧移动
比对所用材料的参数:液体的折射率为1.45, “车辆前照灯”玻璃的折射率参考值在1.47-1.49.的确玻璃粉末的折射率大于液体折射率,镜筒上移,贝克线会向玻璃碎片内侧移动;镜筒下移,贝克线会向液体方向移动,规律验证得很好.
4 学生在规律的寻找中感受学科原理的价值
STEM课程不只是让学生来体验操作技术的,所以上述规律及其成因就让学生自己来寻找吧.
在实际课堂中,笔者和学生们一起讨论了一个基本模型:这里的光学现象会涉及折射的相关知识;楔形是玻璃碎片(粉末)的边缘较为常见的情况,类似于梯形玻璃砖边缘的形状.
考虑到学生只掌握了一侧介质为空气的折射规律,在课堂中,笔者将课本折射定律拓展为:n1sinα1=n2sinα2,即折射率大的介质一侧,光线与法线夹角较小;折射率小的介质一侧光线与法线夹角较大.
于是,学生就利用图4模型进行研究讨论,他们有的是根据折射定律直接进行判断的,也有的是借助梯形玻璃砖和激光笔为工具进行光路观察和仿画的.
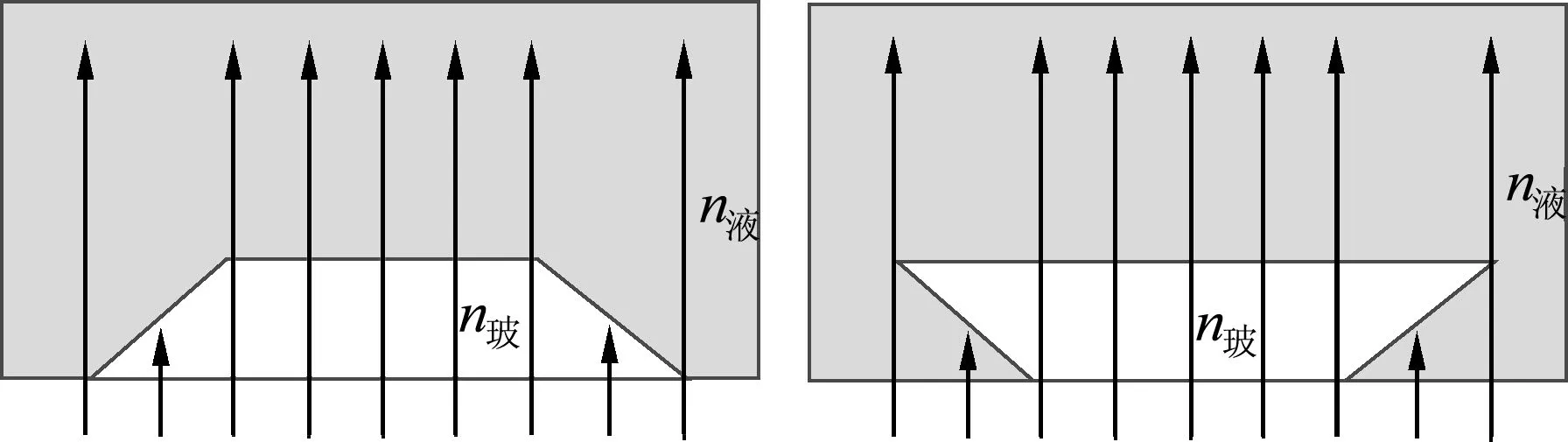
图4 玻璃碎片边缘的两种情况
很快,学生就确定了“n玻>n液”时的光路情形(图5).

图5 “n玻>n液”情况下的光路图
如何解释显微镜下观察到的“亮线”呢?学生在图5中发现,光束有的地方变得密集,有的地方变得稀疏,于是推测光线相交处看起来会比较亮.贝克线的基本成因就这么被学生找到了:密集的地方就是我们看到的贝克线的位置;稀疏的地方就是边界的位置.
再结合显微镜筒升降的过程,学生不难发现图6中,当显微镜聚焦在F1平面的时候,贝克线的位置处在A、B处,而抬高镜筒,聚焦到F2平面时,贝克线的位置就处在A′、B′处,这就有了“n玻>n液”条件下贝克线的移动规律:随着镜筒抬高贝克线会向玻璃碎片内部移动.
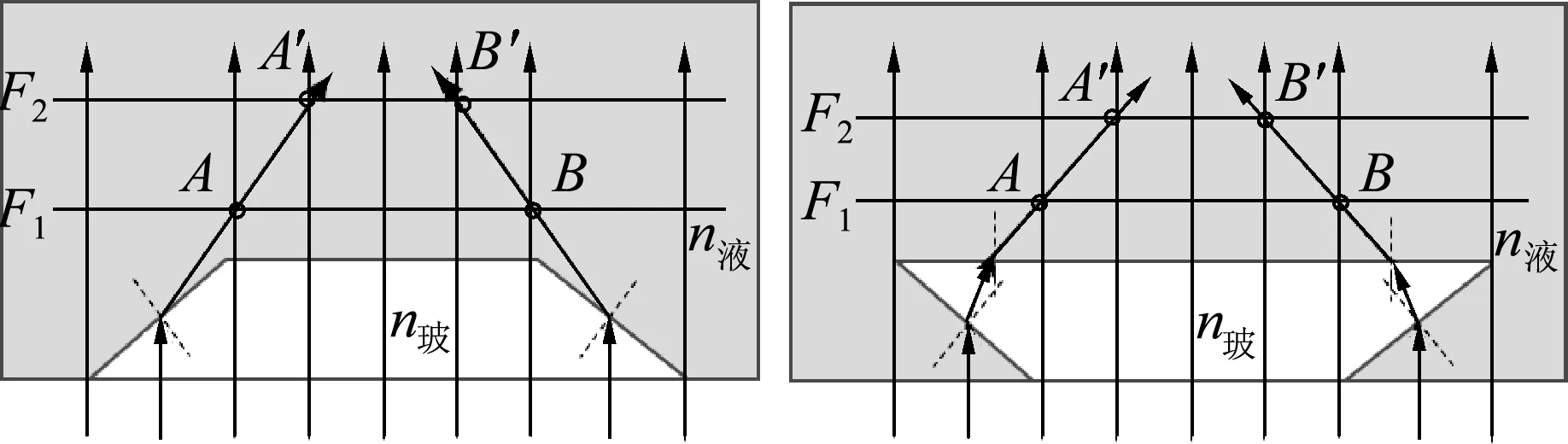
图6 “n玻>n液”,聚焦平面上升,贝克线向内收缩
有了“n玻>n液”的分析基础,“n玻 图7 “n玻 当然,贝克线的成因可能还会涉及全反射现象,基于学生的学习基础,这里也就淡化处理了. 从第一课堂的理论分析来看,学生间的差异还是比较明显的,有的学生已经能够直接通过折射定律判断光路了,而还有部分学生是要依赖玻璃砖和激光笔进行实验观察的.但是,无论哪种情况,通过这个讨论过程,对折射定律都会或多或少有更清晰的认识. 第二堂课上,学生利用生物课上所学的显微镜操作办法,运用观察贝克线法,分别将“凶案现场的玻璃碎片”与折射率为1.45,1.47和1.49的液体进行比对,最终测定“凶案现场的玻璃碎片”的折射率为1.48,同时测定“嫌疑车辆破碎大灯玻璃”的折射率也为1.48. 于是,一个带有迷惑性的疑问又抛给了学生:“是否就此可以判定凶案现场的玻璃碎片就来自于嫌疑车辆?”学生们结合数学上学过的充分条件和必要条件的知识做出了判断:如果凶案现场的玻璃碎片来自于嫌疑车辆,那么两者折射率一定是一样的,但是折射率相同并不能说明两份玻璃来自于同一车辆,也可能是同款其他车辆掉落的. 的确,逻辑判断告诉我们:当两者折射率相同时,只能作出“不能排除凶案现场的碎片来自于嫌疑车辆”的结论.因此,像玻璃碎片这类微量物证很多时候只能成为“类型证据”、还不足以成为“个体证据”. STEM课程融合了科学、技术、工程、数学等多个科学领域的学科知识,这堂课让学生很好地体会到各学科间不是割裂的,在实际应用中多领域的融合是更为常见的. 短短两节课,学生们运用物理规律,找到了一种地理领域(矿物研究)常用的方法,结合生物课所学的操作手法,为物证分析找到了一种技术手段;并据此对一起凶杀案件的物证进行分析,做出逻辑判断.课程形式很新颖,也有趣味性,学生收益颇多,老师的学习受益也不少. 当然,这堂STEM课已经具备了素材和大部分教学材料,教师只要进行课程组织.但即使这样,任课教师已经跨越了几个学科来组织融合.而若要全新开发一个STEM课题,这将对教师持久的好奇心,更广的知识储备,更深入的钻研……有着更高的要求.不过,这也能让教师不轻易被课本固化、被习题圈死;能让学生看到学科的价值,更让课堂教学发挥出勃勃生机.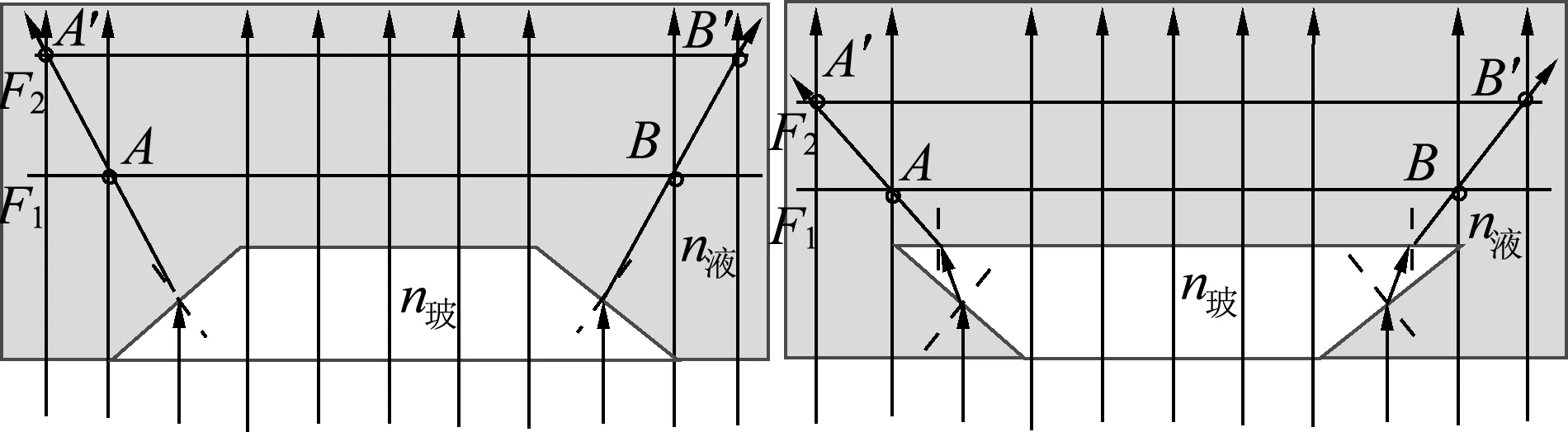
5 STEM课让学生感受各个学科间的融合

