异或门自治布尔网络及物理随机数发生器

杜海鋆，张建国，刘海芳，龚利爽，刘 锋，王云才

1) 太原理工大学新型传感器与智能控制教育部和山西省重点实验室, 山西太原 030024； 2) 太原理工大学物理与光电工程学院, 山西太原030024；3) 广东工业大学信息工程学院, 广东广州510006

自治布尔网络(autonomous Boolean network, ABN)是与离散映射布尔网络相对应的连续动力学系统[1]，具有时间、空间及状态连续性. 与同步布尔网络(synchronous Boolean network, SBN)相比[2]，ABN的相空间从有限维扩展到无限维，使其能够产生更复杂的动力学行为. 作为典型的非线性动力学系统，ABN可以呈现周期振荡、分岔及混沌等非线性状态. 混沌具有对初值敏感、随机及不可预测等特性，在密码学和物理随机数产生等领域极具应用前景[3-5]，激发了广泛的研究兴趣.

ROSIN等[6]首次提出基于三输入异或门结构的16节点ABN，并在现场可编程门阵列(field programmable gate array, FPGA)平台产生单通道速率为100 Mbit/s、并行速率为12.8 Gbit/s的物理随机数. 在这项开创性研究的推动下，ROSIN等[7-8]研究了ABN的受迫和集群同步等问题. 马荔等[9-11]提出不同拓扑结构的ABN，并利用香农熵、自相关性、最大李雅普诺夫指数及记忆时间等指标分析混沌的随机性和不可预测性. DONG等[10]研究时延参数对ABN的影响，指出时延参数的差异性是控制ABN产生混沌的关键. ROSIN等[12-13]则进一步指出，ABN自身存在不稳定机制，在一个拓扑结构固定的网络中，当节点数量超过阈值时，网络会出现从周期态或稳态到混沌态的相变. 与实验研究同步开展的还有ABN的理论建模工作，目前可用于ABN建模的数学方法主要有GHIL等[14-15]提出的布尔延迟方程(Boolean delay equations, BDEs)和GLASS等[16-18]提出的分段线性微分方程(piecewise-linear differential equations, PDEs). 相比于使用BDEs方程建模[19]，基于PDEs方程建立的ABN模型可以较准确刻画ABN电路中的混沌现象[6]，但该模型同样存在不足，如模型未考虑节点的低通滤波效应对ABN的影响，不能合理解释ABN电路实验中出现的周期态到混沌态的相变等物理现象.

针对上述问题，本研究通过理论与实验研究一种基于二输入异或门的18节点ABN. 基于PDEs，通过引入滤波系数建立该ABN的改进数学模型，仿真分析该ABN在不同时延参数和滤波系数情况下的工作状态(周期态和混沌态)，证实滤波系数具有抑制和控制混沌产生的作用.采用通用的电子异或门器件实现ABN电路，实验结果与改进数学模型的数值仿真结果基本一致，ABN电路中存在的“混沌-周期-混沌”2次相变物理现象，可以从改进的ABN数学模型中得到合理解释.实验还发现该ABN电路产生的混沌信号具有良好的随机性、鲁棒性及高带宽特性[20-22]，利用其作为物理熵源可以产生实时速率达100 Mbit/s的高速物理随机数序列，美国国家标准与技术研究院随机性检测结果表明，所产生随机数具有良好的随机统计特性.

1 自治布尔网络

本研究设计的自治布尔网络如图1，其由18个节点构成，每个节点有两路输入和两路输出信号，输入信号分别来自左右两个相邻节点，输出信号也分别传输至这两个节点. 在该ABN中，除节点1执行异或非运算(XNOR)外，其余17个节点(2～18)均执行异或运算(XOR).

使用分段线性微分方程建立该ABN网络的数学模型为

图1 布尔网络示意图Fig.1 Autonomous Boolean network structure

(1)

(2)

2 ABN数值仿真

利用4阶Runge-Kytta方法[23]对系统方程(1)进行数值求解，研究当参数τi, j和τLP取不同值时，ABN的动态变化.

当τi, j均相等时，令τi, j=T(T为常数)，然后连续改变τLP的取值. 仿真结果表明，当所有传输延迟τi, j都相等时，无不动点的ABN网络将处于周期振荡状态.

当τi, j不相等时，令τi, j=T±ε(ε为误差)，然后连续改变τLP的取值. 仿真结果表明，若忽略方程参数τLP， 则无不动点的ABN网络将总是处于混沌状态；当引入参数τLP， 则无不动点的ABN网络将处于混沌或周期状态，表明滤波系数τLP对混沌的产生具有调控或抑制作用. 图2为τLP分别取2.4、3.9及4.3 ns、τi, j=2.7 ns及ε=0.5 ns时，ABN产生的时序和相图.

最大李雅普诺夫指数是衡量非线性系统动力学特征的重要参数指标[24]，可以表征系统在相空间中相邻轨道收敛或发散的平均指数率，当最大李雅普诺夫指数值小于等于0时，系统为周期状态；大于0时为混沌状态；无穷大时为噪声状态. 本研究利用轨道跟踪法中的小数据法[25]，计算得到图2中时间序列的最大李雅普诺夫指数(the largest Lyapunov exponent)分别为L1=0.32 ns-1、L2=0 ns-1及L3=0.26 ns-1.

图2 自治布尔网络输出时序和相图Fig.2 (Color online) Autonomous Boolean network output time series and phase diagrams

3 ABN电路实验

ABN电路实验装置如图3，电路中的节点由德州仪器公司的74AUC1G86异或门芯片构成，其工作电压为0.8～2.7 V. ABN电路中的节点间传输延迟可以表示为τi, j=tpd+tlink(tpd为异或门传输延迟时间；tlink为信号在导线上的传输延迟)，由于tpd≫tlink， 有τi, j≈tpd. 由芯片手册可知，tpd的工作电压越低，tpd值越大. 根据该特性，实验中可以通过改变电路的供电电压达到调谐节点信号传输延迟τi, j的目的. 此外，虽然异或门采用相同半导体工艺制造，但是制造中的微小误差无法避免，因此，在ABN电路中，节点间的传输延迟τi, j总是不相等的.

图3 布尔网络电路实物图Fig.3 (Color online) Prototype board of Boolean circuit

图4为供电电压为1.255、1.310和1.800 V时，ABN电路输出信号(节点2输出)的时序、功率谱和相图. 可见， 当供电电压为1.255 V时，ABN电路的输出信号呈单倍周期振荡，其基频频率为459 MHz；当供电电压逐渐升高至1.310 V时，相图呈现出二倍周期，基频频率为238 MHz；进一步调节供电电压至1.800 V时， ABN电路输出信号随时间的演化变得复杂、无规则，相图出现吸引子，其功率谱由离散谱转变为连续谱，这是混沌信号的典型特征；该信号还具有宽频带特征，其-10 dB带宽可达390 MHz.

图4 不同供电电压时的布尔电路输出信号时序、功率谱及相图Fig.4 (Color online) Time series, power spectra and phase diagrams of the output signals of Boolean circuit with different supply voltages

根据文献[18]方法，分别以ABN电路供电电压和结点2输出信号的相邻两个上升沿之间的时间隔为参数，绘制混沌时序分岔图，如图5(a). 其中，点带状区域(如区域a和d)表示电路进入混沌振荡状态，周期振荡窗口(如区域b和c)则分布其间.ABN电路中低通滤波效应的作用导致周期状态的小范围出现，该现象也与数值仿真结果相互印证，表明ABN数学模型中引入滤波系数的合理性. 此外，宽阔的点带状区域d表明该ABN在较大的供电电压参数范围(1.4～2.7 V)内可以稳定工作于混沌振荡状态，具有较强鲁棒性.

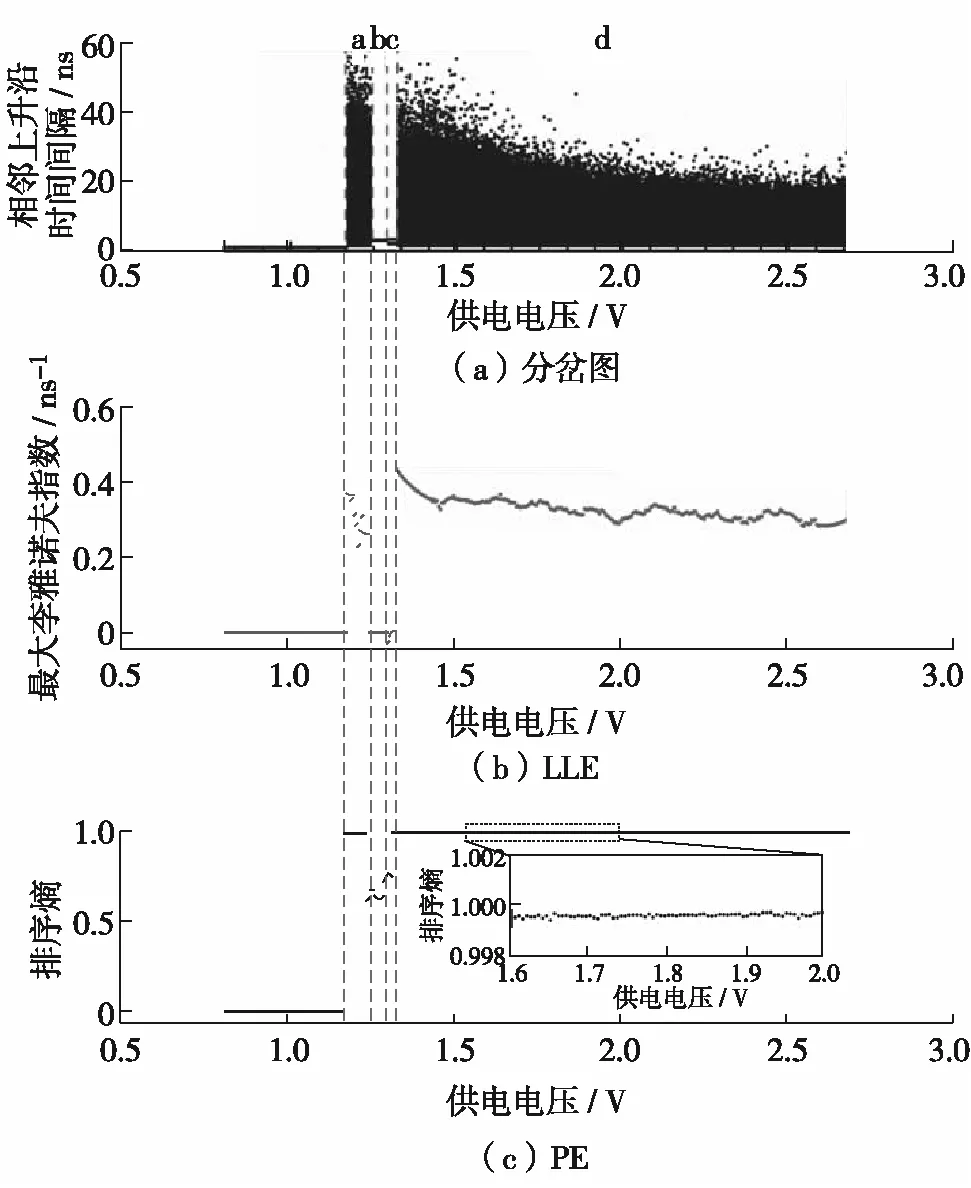
图5 布尔电路输出信号随供电电压增加的变化趋势Fig.5 Output signals of the Boolean circuit as function of the supply voltage

排序熵(permutation entropy, PE)是度量混沌信号随机性的重要指标[21]，定义为

(2)

其中，h(p)为排序熵；π为符号序列；pi(π)为π相对出现频率；M为嵌入维度.对式(2)归一化可得

(3)

对于给定时间序列{x1,x2,…,xi,…,xN}，N为数据长度，使用TAKENS定理将其相空间重构为S=[xt,xt+l,…,xt+(M-1)l]， 其中，l为时间延迟. 对重构后的序列递增排序可得s=[xt+(r1-1)l,xt+(r2-1)l, …,xt+(rM-1)l]. 式(2)中的π为该序列被映射为所有M!种排列中的唯一顺序模式，即π=(r1,r2,…,rM)，r1,r2,…,rM代表重构分量中每个元素的序号. 式(2)中的π为符号序列，则π在时间序列分析中出现的次数可以用f(π)表示，对应概率为

pi(π)=f(π)/(N-(M-1)τ)

(4)

实验中取M=5，l=30. 图5(c)为ABN电路在不同供电电压下的排序熵测量结果.当电路处于混沌状态时，PE的值始终接近于1，表明ABN电路在较大的供电电压参数范围内可以输出的混沌信号具有良好的随机性.

4 基于ABN的物理随机数发生器

ABN电路输出的混沌序列具有高带宽、高熵值以及较强鲁棒性的特点，可作为物理随机数发生器(physical-RNG)的熵源. 本研究设计的physical-RNG如图6，分为ABN熵源和熵提取器2部分. 熵提取器由1个3输入XOR门和4个D触发器构成，其中，利用3个D触发器实现对ABN熵源输出混沌信号(节点1、节点7 和节点13)的采样和量化，产生0、1比特随机序列. 而后随机序列再经3路异或和D触发器波形整形，进一步降低序列中的偏差和相关性，最终产生高质量的物理随机数序列.

图6 物理随机数发生器Fig.6 Physical random number generator

实验中将D触发器的时钟设定为100 MHz，此时该physical-RNG实时输出速率为100 Mbit/s的随机数序列. 当ABN电路供电电压为1.8 V时，τi, j=1 ns，ε=0.4 ns，采集1 Gbit随机数(1 000组， 每组1 Mbit)进行美国国家标准与技术研究院NIST SP 800-22 规定的15项测试，显著水平α设置为0.01，测试结果包括p值及proportion，当p≥0.000 1, proportion≥0.980 6时，表示通过.测试结果如图7，可见，产生的随机数能通过全部测试.

图7 NIST测试结果Fig.7 Typical results of NIST statistical test

表1是基于ABN网络的物理随机数发生器与文献[6,26-28]的对比结果. 可见，本研究提出的物理随机数发生器具有速率高和每比特消耗能量较低的特点.

表1 本研究physical-RNG与其他文献中随机数发生器的性能比较

结 语

本文研究一种二输入异或门的18节点ABN，在PDEs基础上引入滤波系数建立该ABN的改进数学模型，利用4阶Runge-Kytta方法对模型进行求解. 当改变时延参数和滤波系数时，ABN会呈现周期态和混沌态，表明滤波系数具有抑制和控制混沌产生的作用.

实验采用电子器件构建仿真模型，通过改变电路的供电电压调节节点之间的传输延迟，从绘制的分岔图中可以观察到电路的混沌和周期状态，与仿真结果一致. 李雅普诺夫指数和排序熵随电压变化的演变过程表明该网络在宽幅工作电压范围内均可以输出随机性良好的混沌信号，因此，使用100 MHz高频时钟信号对其进行量化采样，高速物理随机数生成速率100 Mbit/s，国际行业标准NIST SP 800-22 测试结果表明，获得的随机比特序列具有良好的统计学特性. 以上仿真和实验研究完善了自治布尔网络熵源结构的理论分析，为混沌物理随机数发生器的深入研究提供参考.