基于多任务贝叶斯压缩感知的电能质量信号重构

王武亮，江 辉

深圳大学物理与光电工程学院，广东深圳 518060

传统的电能质量信号分析方法，都是先按照奈奎斯特采样定律获取数据，然后将数据压缩编码再进行存储或传输，最后对压缩编码的数据进行解压缩处理．然而，一方面电能质量信号扰动类型复杂且变化迅速，这要求采样设备有较高的采样速率，增加了硬件采样成本的同时又产生了大量冗余数据；另一方面，由于电力系统不间断监测的需求，造成每时每刻都要处理海量的采样数据，而采样数据的编码过程计算复杂，消耗了大量计算资源．

贝叶斯压缩感知(Bayesian compressive sensing, BCS)是基于相关向量机[9-10](relevance vector machine, RVM)发展而来． WIPF等[11]提出基于RVM的稀疏贝叶斯学习方法； 2008年，JI等将稀疏贝叶斯理论应用到压缩感知重构算法中，在理论模型中引入噪声项，在信号重构时表现出良好的抗噪性[12]；次年，又提出基于贝叶斯理论的多任务压缩感知，考虑了各待重构任务间数据的内在联系，提高了模型的学习能力和参数估计的精度[13]．

本研究将多任务贝叶斯压缩感知(multitask Bayesian compressive sensing, MT-BCS)理论用于含复杂扰动的电能质量信号的压缩重构研究上，用快速傅里叶变换基对电能质量信号进行稀疏处理，提取稀疏向量的实部和虚部构成两个压缩重构任务，得到两个任务的观测向量后，计算待重构向量的超参数，最后利用观测向量和超参数得到待重构向量的均值进而得到重构信号．通过与正交匹配追踪(orthogonal matching pursuit, OMP)算法和BCS算法的仿真结果对比表明，MT-BCS算法对含复杂扰动的电能质量信号的重构效果更好．

1 MT-BCS

1.1 压缩感知原理

压缩感知包含信号采样压缩与信号重构两部分．信号进行压缩感知的前提条件是信号具有可压缩性，即信号本身是稀疏的，或者在某个变换域下是稀疏的．根据信号稀疏表示理论可知，信号x∈RN×1在N×N的稀疏基Ψ下可表示为x=Ψθ． 其中，Ψ是N×N的正交矩阵；θ∈RN×1是稀疏向量， 当θ中有K个值不为零，则称θ为K稀疏(K≪N)．

信号在观测矩阵Φ下进行线性投影，得到观测值y， 完成信号采样压缩．其中，Φ=[φ1,φ2,…,φN]是M×N的观测矩阵．因此，整个采样压缩过程表示为

y=ΦΨTx=Φθ

(1)

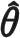
(2)

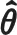
1.2 MT-BCS模型

1.2.1 多任务贝叶斯回归方程

文献[13]在贝叶斯压缩感知的基础上假设观测任务有L个，并且这些观测任务在统计学上互相关联，因此，L个稀疏向量θi通过L个观测矩阵Φi得到L个观测值为

yi=Φiθi+ni

(3)

其中，yi∈RMi×1, 表示L个观测值{yi}i=1,2,…,L； 通常每个观测任务使用不同的随机观测矩阵Φi,Φi∈RMi×N,i=1,2,…,L；L个稀疏向量θi∈RN×1；ni∈RMi×1是每个观测任务引入的噪声，本研究假设ni服从均值为0，方差为σ2的多元高斯分布．

给定观测值yi，则稀疏向量θi和方差σ2的似然函数为

(4)

同时，定义α0=σ-2为噪声逆方差，服从参数为(a,b)的伽玛分布．将α0集成到θi的先验分布中，则可避免对α0的估计，增强了算法的鲁棒性．定义θi服从0均值高斯先验，即

(5)

其中，L个稀疏向量θi共享同一超参数α， 此共享机制利用了各组数据的内在联系，使不同组的观测值数据可共同影响α的估计值，这正是多任务贝叶斯估计的精髓．

给定超参数α和测量值yi， 结合式(4)和式(5)，利用贝叶斯定理可得θi的后验分布函数为

p(θi|yi,α)=

(6)

其中，

μi=ΣiΦTiyi

(7)

Σi=(ΦTiΦi+A)-1

(8)

这里，对角矩阵A=diag(α1,α2, …,αN)．

θi的后验分布函数为多元Student-t分布，它具有很好的健壮性，由于其概率密度函数没有指数的限制，所以在数据有噪声时鲁棒性更强．

1.2.2 超参数估计

利用最大化边际似然函数估计超参数α．由式(4)和式(5)得到α的边际似然函数的对数为

ln|Bi|]+const

(9)

其中，Bi=I+ΦiA-1ΦTi； const为表示θ的一个常量．利用直接微分法或最大期望算法都可通过式(9)求得α的点估计为

j=1, 2, …,N

(10)

为解式(10)，文献[13]通过式(7)、式(8)和式(10)迭代计算出α的估计值．Φi最初包含N个候选基函数然后逐渐优化删除一些基函数．式(8)需要计算N×N矩阵的逆，需要O(N3)的计算复杂度和O(N2)的空间复杂度，此操作在N很大时的计算量巨大且耗时严重．因此，文献[13]提出了快速算法．在该快速算法中，Φi从一个初始基函数开始，根据需要在Φi中添加或删除当前基函数，并且根据矩阵逆引理，降低了式(8)的计算复杂度．该快速算法因其任一步中Φi包含的基函数数量相比N都很低，因此算法的计算复杂度更低．

(11)

其中，Bi, -j是Bi移除了Φi,j的项．因此，式(9)可改写为

L(α-j)+l(αj)

(12)

其中，α-j是α移除了第j个元素剩下的部分；si, j为稀疏因子，表征当前基函数与模型中已有基函数的重叠程度，si, j=ΦTi, jB-1i, -jΦi,j；qi, j为质量因子，表征当前基函数与排除了当前基函数的模型的对齐程度，qi, j=ΦTi, jB-1i, -jyi；gi, j=yTiB-1i, -jyi+2b；l(αj)表示对向量α中的一个元素αj求对数．

对式(12)运用直接微分法求αj的极值．结果除了明显解αj=∞外，其他的解不能解析地表示，但可近似为

(13)

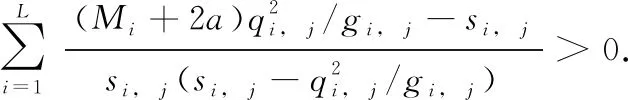
通过分析多元Student-t函数性质可知，αj=∞等同于θi, j=0，Φi,j可从Φi中移除，因此，求αj的极值就是控制从Φi中添加和删除Φi,j的操作．如果对候选Φi,j按照顺序执行这些操作，就得到了有效的快速算法．

2 基于MT-BCS的电能质量信号重构

从压缩感知理论知道，要对某个信号进行压缩感知，该信号必须是稀疏的或者在某个变换域下是稀疏的．电网中含有复杂扰动的电能质量信号并不是稀疏信号，但在一些稀疏基的投影下是稀疏信号．在电能检测领域，快速傅里叶变换基和小波基是运用最多并且较为成熟的稀疏基，而快速傅里叶变换基结构简单，运算速度快，因此，本研究选择快速傅里叶变换基为稀疏基．

将电能质量信号通过快速傅里叶变换得到稀疏向量θ．θ是复数，取θ中的实部θR和虚部θI构成两个压缩重构任务，通过MT-BCS算法同时对θR和θI进行压缩重构．因为θR和θI之间的稀疏度很相似， MT-BCS算法通过共享超参数机制充分考虑到θR和θI数据的内在联系，提高了模型的学习能力和重构精度．

电能质量信号用多任务贝叶斯压缩感知算法压缩重构的具体步骤为

1)信号的稀疏变换．将电能质量信号x通过快速傅里叶变换得到稀疏向量θ，再将其实部θR和虚部θI作为两个压缩重构任务得到两组观测值yR和yI．

3 仿真与结果分析

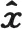
(14)

(15)

其中，t∈[0, 0.20]． 仿真采用的电能质量信号模型如表1．

表1 电能质量信号模型

3.1 稳态电能质量信号仿真分析

对表1中的稳态电能质量信号进行仿真实验，得到表2稳态电能质量信号的仿真数据，以间谐波信号的仿真实验为例对比分析的性能．图1给出了当测量数M从50个增至250个时，3种算法对间谐波信号在不同噪声情况下压缩重构的RMSE和SNR值的曲线图．表2给出了3种算法在M=128时，对稳态电能质量信号在不同噪声情况下进行压缩重构的RMSE和SNR值．

结合表2和图1(a)可见，重构不含噪声的间谐波信号时，OMP算法的RMSE值3.350×10-15最小， MT-BCS算法的RMSE值7.190×10-5略大，BCS算法的RMSE值5.110×10-4最大；当间谐波信号中加入噪声且噪声方差(σ2)增大后， BCS算法的RMSE值0.026最小，MT-BCS算法的RMSE值0.035略大，OMP算法的RMSE值0.047最大．结合表2和图1(b)可见，重构不含噪声的间谐波信号时，OMP算法的SNR值666.560最大，MT-BCS算法的SNR值192.330次之，BCS的SNR值156.010最小；当间谐波信号中加入噪声且噪声方差增大后，BCS算法的SNR值72.390最大，MT-BCS 算法的SNR值66.810次之，OMP算法的SNR值60.780最小．

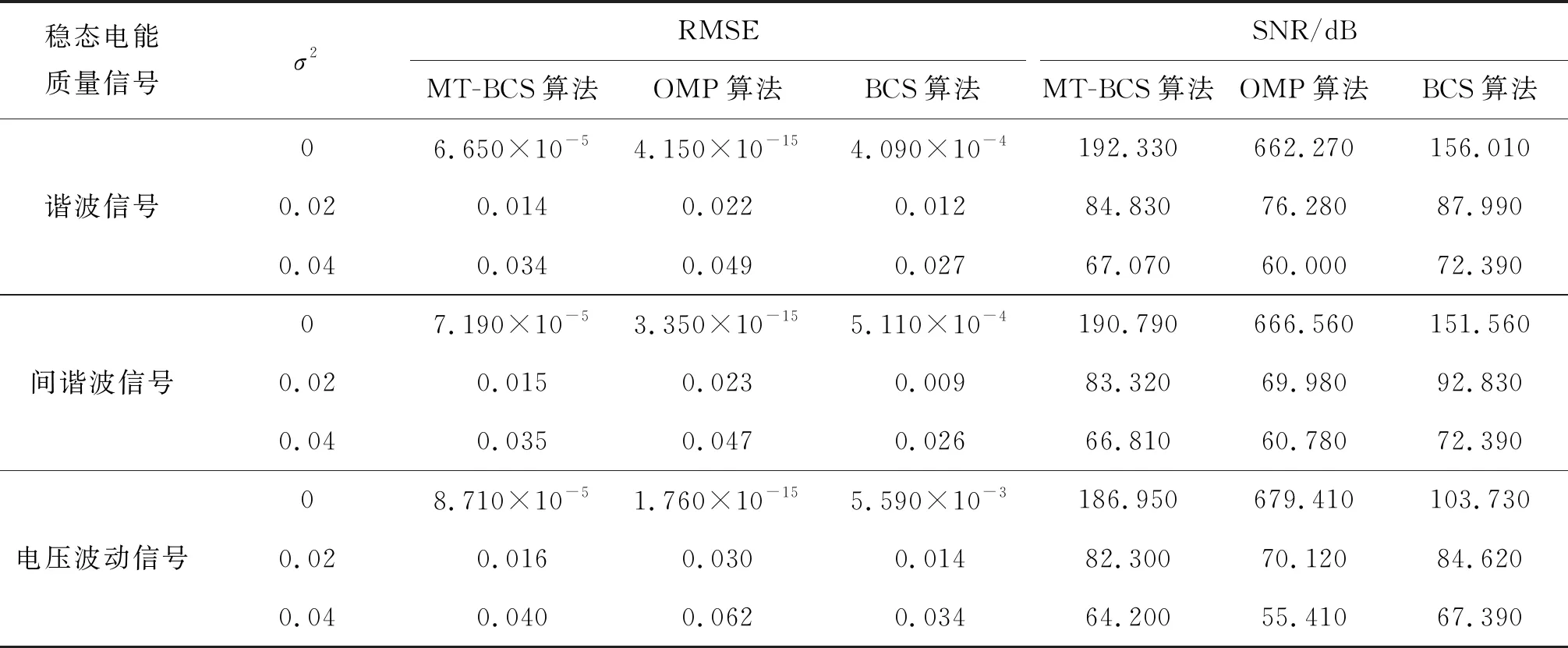
表2 稳态电能质量信号仿真数据(M=128)

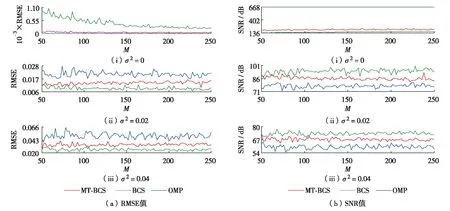
图1 不同噪声情况下3种算法重构间谐波信号的数据曲线Fig.1 The data curve of the reconstructed interharmonics signal by three algorithms under different noises

由表2可见，OMP算法在重构不含噪声的稳态电能质量信号时，效果远优于MT-BCS算法和BCS算法，这是因为此时的稳态电能质量信号扰动简单又不含噪声．当稳态电能质量信号中加入噪声后，MT-BCS算法和BCS算法的抗噪性要强于OMP算法，贝叶斯理论在建立模型的时候就已经引入了测量噪声和随机高斯噪声，这令基于贝叶斯理论的算法拥有比OMP算法更强的抗噪性．重构含有噪声的稳态电能质量信号时，MT-BCS算法的重构效果略逊于BCS算法，这是因为此时信号扰动简单，信号稀疏变换后稀疏度很小，而MT-BCS算法待估计超参数共享，因此超参数累积的误差对MT-BCS算法的影响较大．

3.2 暂态电能质量信号仿真分析

对表1中的暂态电能质量信号进行仿真实验，以短时谐波信号为例，对比分析MT-BCS算法与OMP算法和BCS算法的性能．图2给出了当M从50增至250时，3种算法对短时谐波信号在不同噪声情况下重构的RMSE和SNR值曲线图．表3给出了当M=128时，3种算法对暂态电能质量信号在不同噪声情况下重构的RMSE和SNR值．

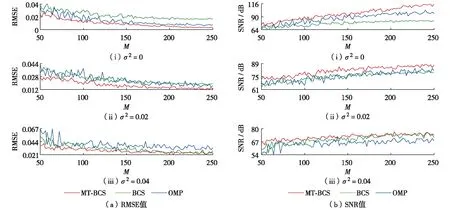
图2 不同噪声情况下3种算法重构短时谐波信号的数据曲线图Fig.2 The data curve of the reconstructed short-time harmonics signal by three algorithms under different noises

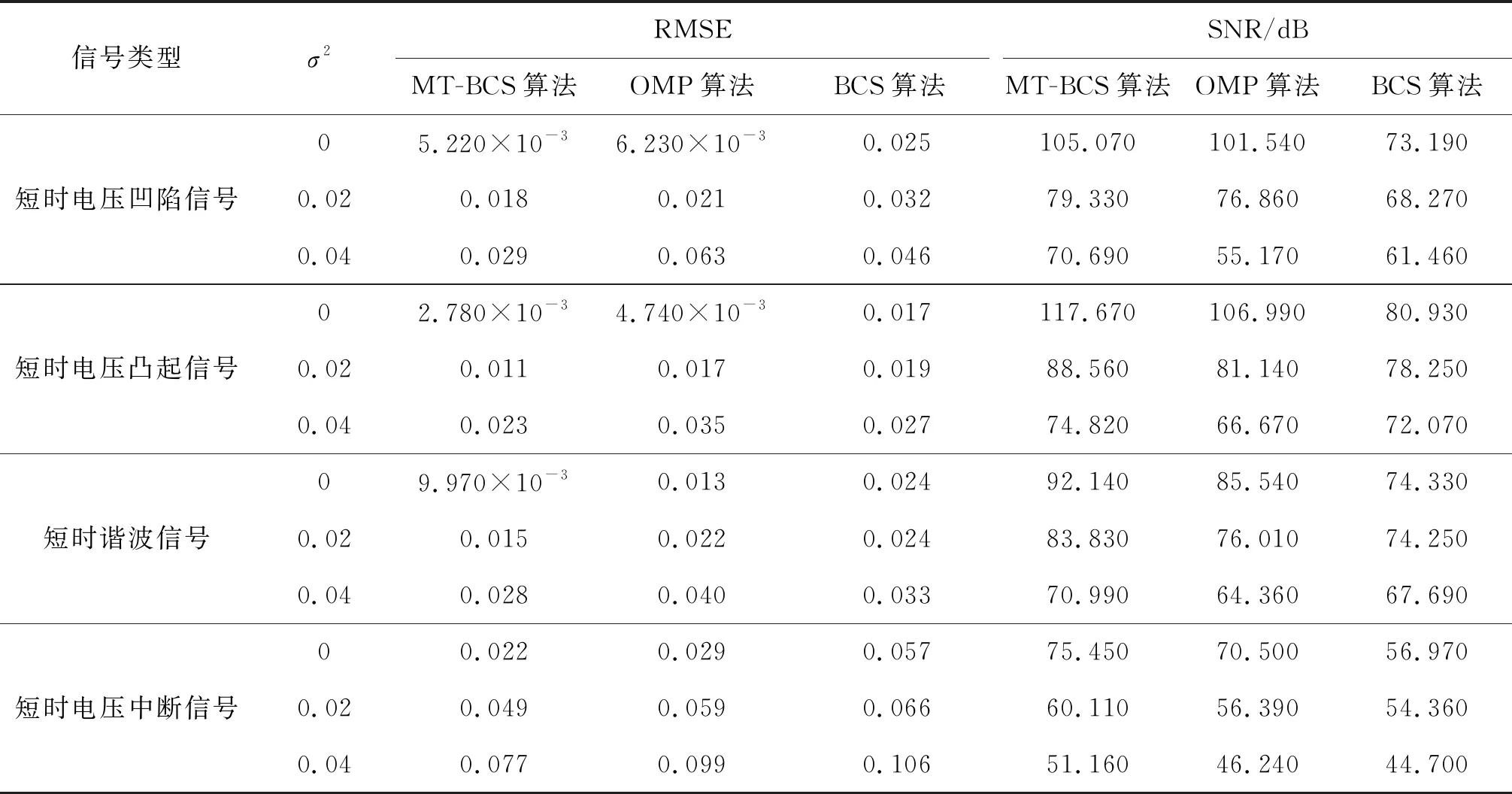
表3 暂态电能质量信号仿真数据(M=128)

由图2(a)和表3可见，当重构不含噪声的短时谐波信号时，MT-BCS算法的RMSE值9.970×10-3在3种算法中最小，OMP算法的RMSE值0.013较大，BCS算法的RMSE值0.024最大；当短时谐波信号中加入噪声及噪声方差增大后，MT-BCS算法的RMSE值0.028在3种算法中依旧保持最小，BCS算法的RMSE值0.033略大，OMP算法的RMSE值0.040最大．结合图2(b)和表3可见，当重构不含噪声的短时谐波信号时， MT-BCS算法的SNR值92.140在3种算法中最大，OMP算法的SNR值85.540次之，BCS算法的SNR值74.330最小；当短时谐波信号中加入噪声及噪声方差增大后，MT-BCS算法的SNR值70.990在3种算法中依旧保持最大，BCS算法的SNR值67.690次之，OMP算法的SNR值64.360最小．从图2(a)和图2(b)还可看出，在M很小时，MT-BCS算法的重构效果也优于OMP算法和BCS算法，说明MT-BCS算法的性能在压缩采样不完备的情况下依然稳定，而且采样率越低此优势越明显．在重构暂态电能质量信号时共享超参数机制使得MT-BCS算法更好地利用了实部与虚部数据的内在联系，拥有更精确的估计值和更强的抗噪性，重构效果明显优于BCS算法和OMP算法．但是，MT-BCS算法同时重构实部和虚部两个任务，计算过程更复杂，这也牺牲了一定的运算时间．

3.3 复杂电能质量信号仿真分析

图3给出了当M从50增至250时，3种算法对复杂信号在不同噪声情况下重构的RMSE和SNR值的曲线图．表4给出了当M=128时3种算法对复杂信号在不同噪声情况下重构的RMSE和SNR值．

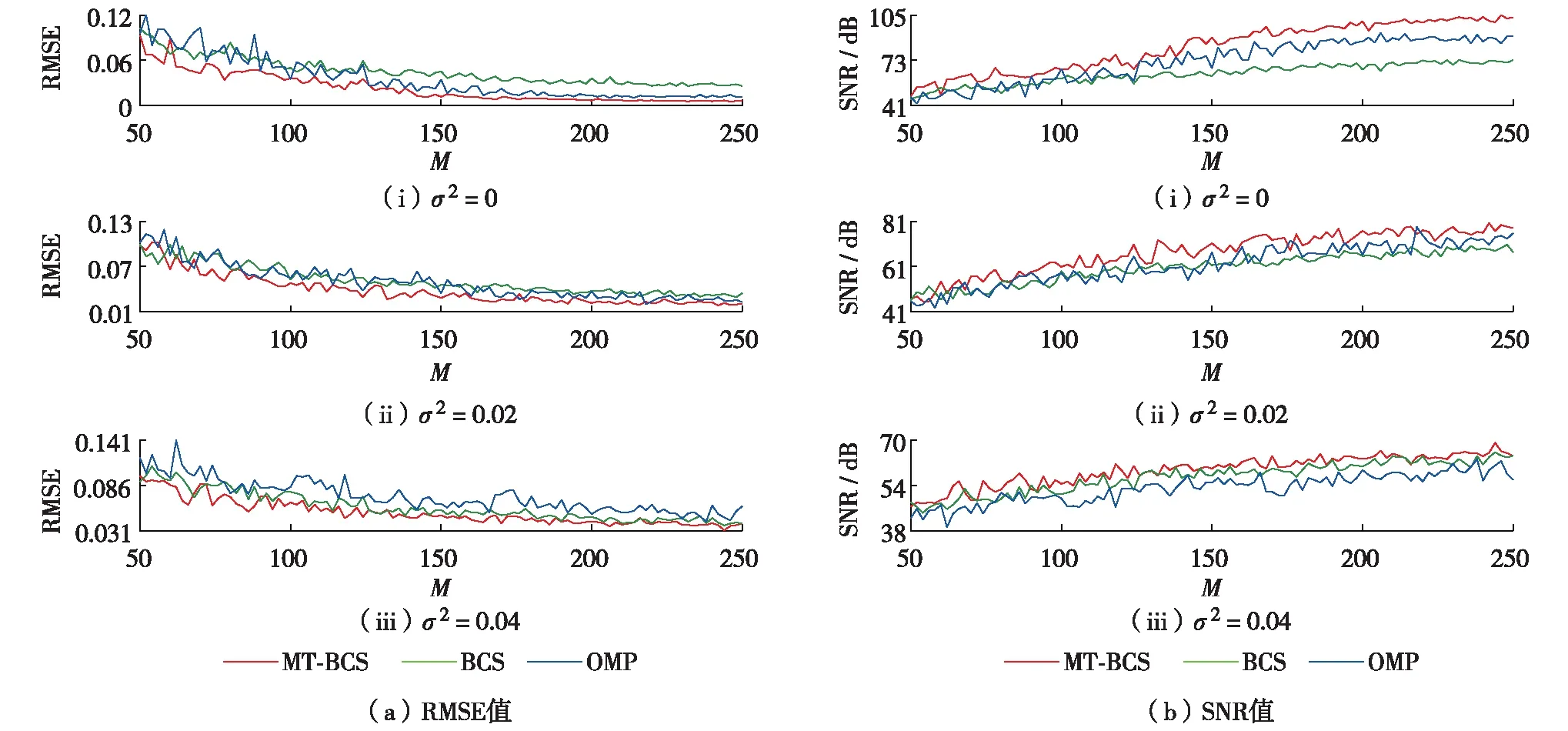
图3 不同噪声情况下3种算法重构复杂信号的数据曲线图Fig.3 The data curve of the reconstructed complicated signal by three algorithms under different noises

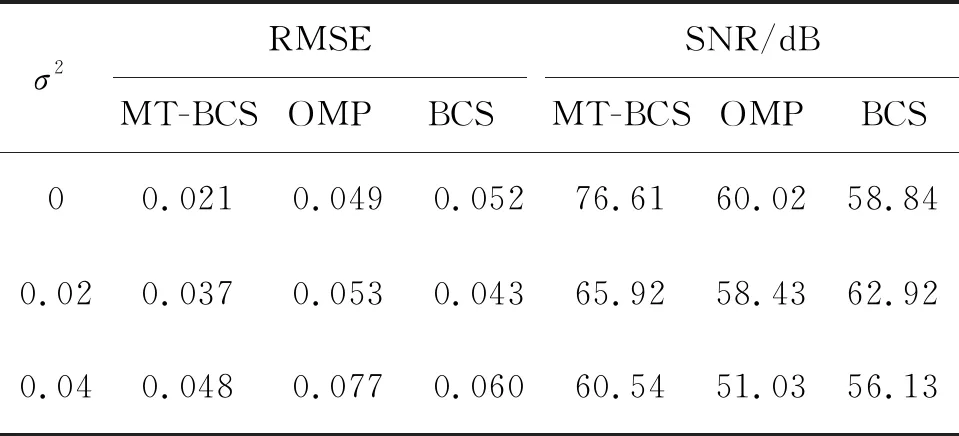
表4 复杂电能质量信号仿真数据(M=128)Table 4 Simulation data of complicated power quality signal (M=128)

结合图3(a)和表4可见，当重构不含噪声的复杂信号时，MT-BCS算法的RMSE值0.021在3种算法中最小，OMP算法的RMSE值0.049较大，BCS算法的RMSE值0.052最大；当复杂信号中加入噪声及噪声方差增大后，MT-BCS算法的RMSE值0.048依旧保持最小，BCS算法的RMSE值0.060略大，OMP算法的RMSE值0.077最大．结合图3(b)和表4可见，当重构不含噪声的复杂信号时， MT-BCS算法的SNR值76.610在3种算法中最大，OMP算法的SNR值60.020次之，BCS算法的SNR值58.840最小；当复杂信号中加入噪声及噪声方差增大后，MT-BCS算法的SNR值60.540依旧最大，但BCS算法的SNR值56.130比OMP算法的SNR值51.030大．可以看出，MT-BCS算法也适用于压缩重构扰动更加复杂的电能质量信号，且表现出出色的重构效果，更适合于含复杂扰动的电能质量信号的压缩重构．

结 语

将多任务贝叶斯压缩感知理论用于含复杂扰动的电能质量信号的压缩重构研究中．对OMP算法和BCS算法进行仿真，结果表明：① 在压缩重构含复杂扰动的电能质量信号时，MT-BCS算法对电能质量信号的重构效果更出色，重构精度更高；② MT-BCS算法在压缩比很小时依然能够保持良好的稳定性，在压缩比很小时重构效果优于OMP算法及BCS算法，体现了MT-BCS算法在低压缩采样率时的巨大优势，能够以更低的压缩比压缩重构信号，有效节省了存储空间．③ 当信号含有噪声时，MT-BCS算法的重构效果优于OMP算法及BCS算法，说明该算法具有更强的抗噪性，这在压缩重构含有大量噪声的电能质量信号时优势明显．但是，MT-BCS算法在追求高重构精度和更强抗噪性的同时，牺牲了算法的运行时间，致使算法运行时间较长．综上所述，MT-BCS算法能够适应含各种复杂扰动的电能质量信号的压缩重构．