求解不可微凸优化问题的充分下降共轭梯度法
黄元元
(河南科技大学 数学与统计学院, 河南 洛阳 471023)
0 引言
考虑无约束优化问题:
minf(x),x∈Rn,
(1)
其中f:Rn→R是连续的凸函数,但不一定可微。该问题在机器学习、数据分析、信号处理和图像处理等领域[1-4]均有应用。若f是连续可微的,则共轭梯度(conjugate gradient,CG)法是求解问题(1)较常用且有效的一类方法。若f为连续的凸函数但不可微,则求解问题(1)的较早算法是邻近点方法 (proximal point methods, PPM)[5-6],将问题(1)转化为极小化问题:
minF(x),x∈Rn,
(2)
进行求解,其中:
(3)
为函数f的Moreau-Yosida正则化函数。鉴于两者解集相同[7],文献[8]引入近似求解函数F(x)的值及其梯度值的策略,在邻点算法基础上设计了求解问题(2)的一种切实可行的算法,该算法是Moreau-Yosida正则化和一般牛顿法的结合。之后,文献[9]提出求解问题(2)的两项和三项Polak-Ribière-Polyak(PRP)共轭梯度法,文献[10-11]提出求解问题(2)的改进的PRP共轭梯度法和Hestenes-Stiefel(HS)共轭梯度法,文献[12]提出共轭参数非负的改进共轭梯度法。但在求解光滑的无约束优化问题上非常具有优势且满足充分下降条件的CG_DESCENT方法[13-14],在求解问题(1)方面却未有相关文献进行研究。本文将基于CG_DESCENT方法求解光滑无约束优化问题的更一般形式[15],给出求解问题(1)的一类具有充分下降条件的共轭梯度法,并证明它们在不依赖于任何线搜索的情况下满足充分下降条件且全局收敛。
1 预备知识
下面给出本文要用到的基本命题和引理,具体证明过程请参阅相关文献。
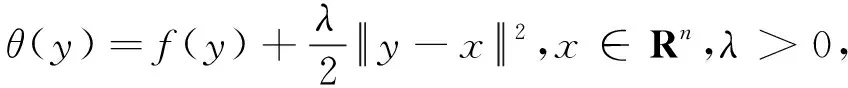
命题1[7]设函数F如式(3)定义,则函数F是有界的凸函数且处处可微,其梯度为g(x)=▽F(x)=λ(x-p(x))。该梯度映射g:Rn→Rn是逆强单调的,即
并且是λ-Lipschitz 连续的,即
(4)
命题2[7]若x*是问题(1)的最优解,则x*也是问题(2)的最优解,且与以下几条陈述相互等价:
(i)x*=p(x*);(ii)▽F(x*)=0;(iii)f(x*)=f(p(x*));(iv)f(x*)=F(x*)。
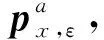
(5)
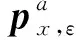
(6)
(7)
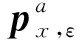
(i)F(x)≤Fa(x,ε)≤F(x)+ε;
2 算法设计
本文利用Moreau-Yosida正则化策略,给出求解不可微优化问题(1)的算法。若已知当前迭代点xk,通过xk+1=xk+αkdk计算新的迭代点,步长αk通过线搜索得到,搜索方向dk为:
(8)
算法1:
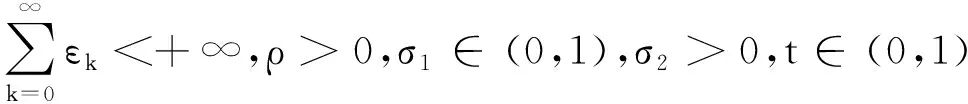
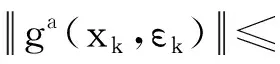
步骤3 对α∈{ρtj|j=0,1,2,…},选取使得不等式
(9)
成立的最大的α作为步长αk。计算xk+1=xk+αkdk。令k:=k+1,并转至步骤2。
3 收敛性分析
为了分析算法1的收敛性质,首先给出以下假设。

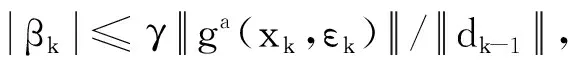
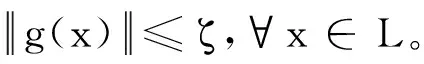
(10)
引理2若ξk≠0,θk≥1/4,且dk由式(8)生成,则对任意的k≥0都有:
(11)
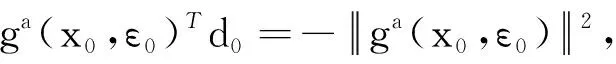
(12)
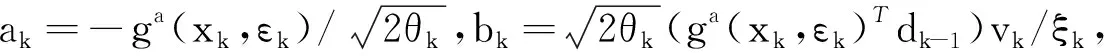
引理2证毕。
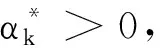
(13)
证明假设在第k次迭代仍未找到最优解,对所有的j=0,1,2,…,不等式(9)均不成立,即
Fa(xk+ρtjdk,εk+1)>Fa(xk,εk)+σ1ρtjga(xk,εk)Tdk-σ2ρ2t2j‖dk‖2+εk。
(14)
将式(14)两边同时关于j取极限,得:
Fa(xk,εk+1)≥Fa(xk,εk)+εk。
(15)
由引理1中(i)可知:Fa(xk,εk+1)≤Fa(xk)+εk+1且Fa(xk,εk)≥Fa(xk)。将这两个不等式与式(15)相结合得εk+1≥εk,这与εk+1<εk相矛盾。从而步长αk是有定义的,可以在有限次尝试后得到。
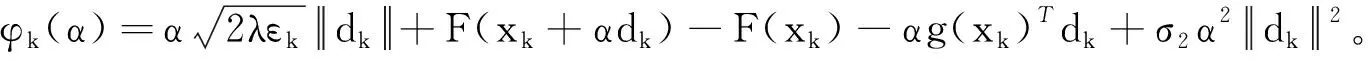
(16)
由引理1可知:
Fa(xk+αkdk,εk+1)≤F(xk+αkdk)+εk+1;
(17)
F(xk)≤Fa(xk,εk);
(18)
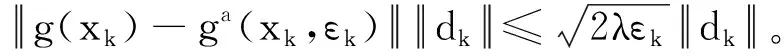
(19)
由式(17)~式(19)得:
F(xk+αkdk)-F(xk)-αkg(xk)Tdk。
(20)
由式(11)可知:ga(xk,εk)Tdk<0。因为σ1∈(0,1),则
ga(xk,εk)Tdk≤σ1ga(xk,εk)Tdk,
将其与不等式(16)和不等式(20)相结合得式(13)。
引理3证毕。
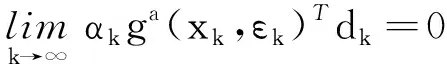
证明由线搜索准则可知,对于步长αk,式(9)成立,即
(21)
结合引理2,有:
Fa(xk+1,εk+1)≤Fa(xk,εk)+εk。
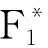
(22)
(23)

选取K∈K1且K≥max{K1,K2,K3}。对所有的k≥K,结合式(22),有:
(24)
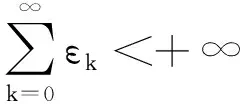
引理4证毕。
定理1若假设1和假设2成立,则算法1产生的序列{xk}的任何聚点都是问题(1)的最优解。
证明设x*是序列{xk}的一个聚点,必存在{xk}的一个子列{xk}k∈K收敛到x*。由式(4)和引理1中(iii)可知:
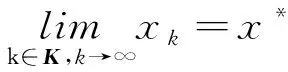
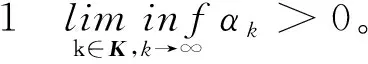
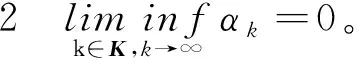
由引理1中(i)可知:
F(xk)≤Fa(xk,εk);
(25)
Fa(xk+ρ-1αkdk,εk+1)≤F(xk+ρ-1αkdk)+εk+1。
(26)
由步长αk的选取准则可知:
将其与式(25)、式(26)及εk+1<εk相结合,得:
从而有:
(27)
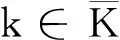
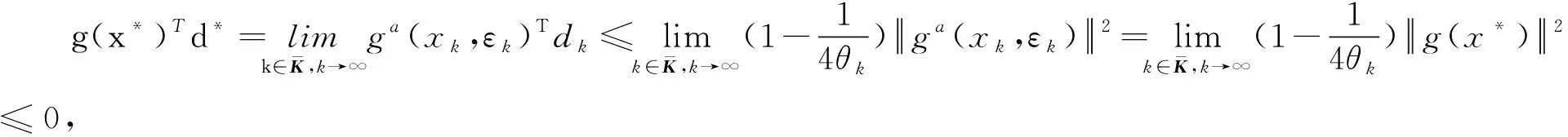
定理1证毕。
4 结论
通过非精确求解Moreau-Yosida正则化函数的函数值和梯度值,将被广泛认同的求解无约束优化问题的有效共轭梯度算法推广到求解非光滑优化问题上,从理论上分析了算法的可行性,具有一定的理论价值。

