十字线结构光视觉传感器的标定方法研究

毕 超 郝 雪 周 鹏

(北京航空精密机械研究所 精密制造技术航空科技重点实验室，北京 100076)

1 引 言

近年来，我国的先进制造装备与技术取得了飞速发展，对复杂零部件的加工精度和生产效率提出了越来越高的要求，这就使得现代测量技术及仪器要逐渐发展成为必备的生产部件或设备，应用于工业现场并参与到制造过程中[1]。随着测试计量技术及其相关学科的长足进步，基于光学三角法测量原理的结构光三维视觉测量技术，由于实现容易、操作方便、成本低廉和应用灵活，并且具备在线、非接触和实时测量的特性和潜力，在科学研究和工业生产中得到了越来越广泛的应用。

依据结构光三维视觉测量技术研发出的十字线结构光视觉传感器，主要由光学投射器和摄像机构成[2]。对于此类传感器来说，其数学模型的建立与结构参数的标定是确保测量功能实现的关键[3]。目前，许多学者在结构光视觉传感器的数学建模和标定方法方面开展了研究工作。王金桥等建立了线结构光视觉传感器的数学模型，根据张正友方法并结合L-M非线性优化算法标定出了摄像机的内、外部参数，并通过引入辅助线激光而形成双激光交点，完成了对线结构光平面的精确标定[4]。高金刚等基于高精度的异形量块，通过提取光平面与异形量块的交线中心线，并采用GA-RBF算法实现了对线结构光传感器的标定，标准偏差均值约为0.008%[5]。邹媛媛等针对三线结构光视觉传感器，设计了由高精度条板与精密平移台构成的靶标，并采用支持向量机方法实现了对传感器的直接标定[6]。然而，这些标定方法采用了较为复杂的辅助设备和解算方法，灵活性和便捷性较差，不具备广泛的适用性。

针对基于结构光三维视觉测量原理的十字线结构光视觉传感器，本文研究了其结构参数的标定方法。建立了该传感器的透视投影测量模型，并通过摄像机标定、光条中心线提取和结构光平面解算等过程解算出了模型中的未知量，从而完成了传感器的结构参数标定。该标定方法无需高成本的标定靶标和复杂的操作过程，并且可以提高标定效率、降低劳动强度，特别适合于现场组建基于十字线结构光视觉传感器的三维测量系统。

2 系统组成

为了实现被测物体的表面轮廓信息的快速、精确获取，本文基于结构光三维视觉测量原理搭建了一套非接触式的十字线结构光视觉传感器，如图1所示。该传感器主要由摄像机、光学投射器和夹持工装构成，其中，摄像机选用大恒图像公司的MER-500-7UM型工业数字面阵相机，其传感器为ON MT9P031行曝光CMOS，靶面尺寸为1/2.5″，分辨率为2592×1944，帧率为7fps，单个像元的大小为2.2μm×2.2μm。为了将被测目标成像在摄像机的靶面上，选用了日本CBC公司的M0814-MP2型百万像素定焦镜头，其焦距为8mm，最大兼容靶面尺寸为2/3″。光学投射器选用小功率的通用十字线激光器，其输出绿色激光的波长为520nm，并且线宽可调。

图1 十字线结构光视觉传感器Fig.1 Cross structured light sensor

3 数学模型

在十字线结构光三维视觉测量中，摄像机与十字线激光器之间形成三角几何约束。由十字线激光器向被测物体投射一束极细的、呈“十字线”模式的结构光，会在空间中形成两个连续、相互垂直且具有一定厚度的光平面。当这两个光平面在传播过程中与被测物体相遇时，将在物体表面上形成两条受表面形貌、起伏特性等调制的投影光条特征[7]。为了确定投影光条上的采样点的二维图像坐标与其三维空间坐标之间的映射关系，从而重建和恢复出被测物体的三维轮廓与表面形貌，本文以透视投影理论为基础，建立了该十字线结构光视觉传感器的数学模型，即透视投影测量模型，其建模过程如图2所示。

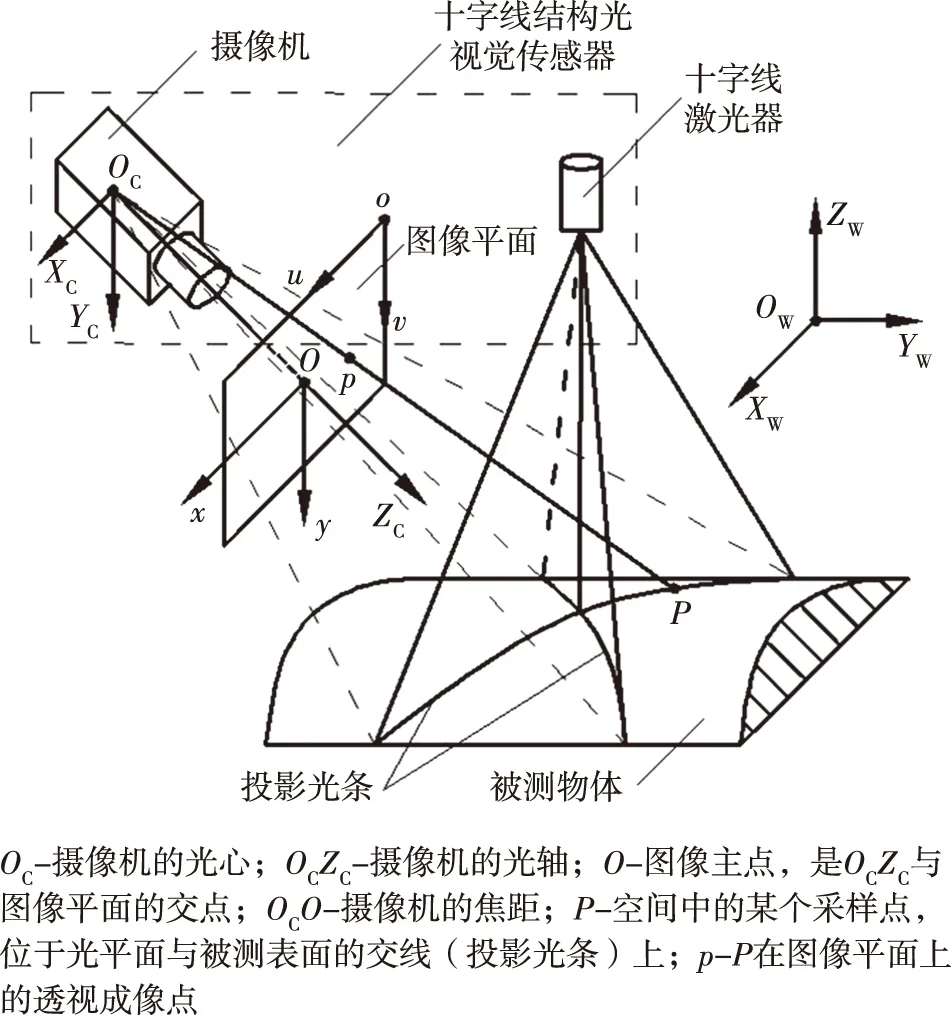
图2 传感器的数学模型Fig.2 Mathematical model of the sensor

在应用过程中，为了能够将由摄像机采集到的二维图像数据转化为三维物理测量数据，并最终转换到统一的世界坐标系中，本文在传感器的数学模型中建立了4个直角坐标系，分别为图像像素坐标系o-uv、图像物理坐标系O-xy、摄像机坐标系OC-XCYCZC和世界坐标系OW-XWYWZW。其中，o-uv和O-xy为平面坐标系，用于表征二维图像空间；OC-XCYCZC和OW-XWYWZW为空间坐标系，用于表征三维物理空间。

设采样点P在OW-XWYWZW和OC-XCYCZC下的齐次坐标分别为(XW,YW,ZW,1)和(XC,YC,ZC,1)，二者之间存在如下的转换关系

(1)

式中：R——3×3阶的旋转矩阵；T——3×1阶的平移矩阵。R和T描述了OW-XWYWZW与OC-XCYCZC之间的转换关系，用于表征摄像机在世界坐标系中的位置和姿态[8]，属于摄像机的外部参数。

设P的像点p在o-uv和O-xy下的齐次坐标分别为(u,v,1)和(x,y,1)，在理想透视变换条件下，二者的转换关系为

(2)

式中：dx、dy——分别为单个像素在x轴、y轴方向上的长度，mm/pixel；(u0,v0)——图像主点O在o-uv中的像素坐标，pixel。

在不考虑成像畸变的条件下，采样点P与其像点p之间满足几何共线约束准则，即采样点P、像点p和摄像机光心OC在同一条直线上。因此，p的图像物理坐标(x,y)与P在OC-XCYCZC下的三维坐标(XC,YC,ZC)之间的转换关系为

(3)

式中：f——摄像机的有效焦距，mm。

在公式(2)和公式(3)中，dx、dy、u0、v0和f均由摄像机本身决定，因而属于摄像机的内部参数。联立公式(1)～公式(3)，可以得到o-uv与OW-XWYWZW之间的转换关系，从而将采样点P的图像像素坐标(u,v)转换为其世界坐标(XW,YW,ZW)。然而，此过程中的约束条件尚不充分，已知u、v还不足以求解出与之相对应的XW、YW和ZW，还需要进一步求解出两个光平面在世界坐标系中的表达式来作为补充约束条件。一般情况下，光平面方程的基本形式为

A·XW+B·YW+C·ZW+D=0

(4)

式中：A、B和C——分别为光平面方程的系数，D——光平面方程的常数项。

由于采样点P同时位于世界坐标系内和光平面上，可以将公式(1)～公式(4)联立起来，从而建立起十字线结构光视觉传感器的数学模型，如公式(5)所示，这样就可以形成充足的约束条件以通过P的图像像素坐标(u,v)解算得到P在OW-XWYWZW中的三维坐标(XW,YW,ZW)。

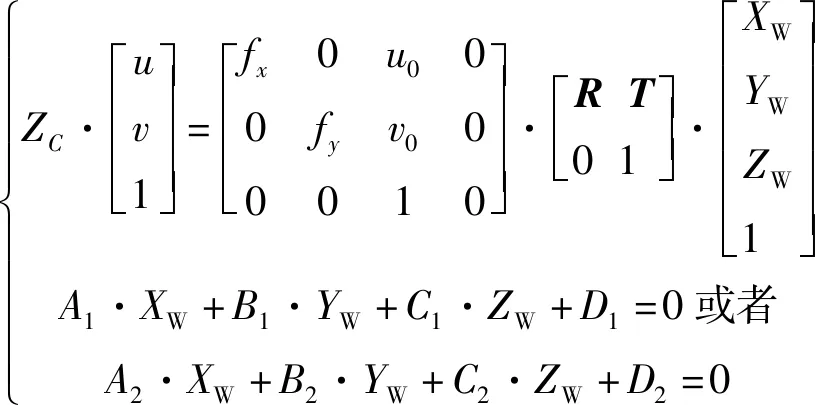
(5)

式中：A1、B1、C1和D1——分别为光平面π1的方程参数；A2、B2、C2和D2——分别为光平面π2的方程参数；fx——x轴上的尺度因子，fx=f/dx；fy——y轴上的尺度因子，fy=f/dy。

4 标定过程与步骤

为了使所搭建的十字线结构光视觉传感器能够实现测量功能，需要通过标定过程确定公式(5)中的R、T、u0、v0、fx和fy等摄像机参数以及A1、B1、C1、D1、A2、B2、C2和D2等光平面参数。同时，十字线结构光视觉传感器的核心技术也在于标定算法，主要包括摄像机标定、光条中心线提取和结构光平面标定三个环节。

4.1 摄像机标定

获取摄像机的内部参数u0、v0、fx、fy和外部参数R、T的过程，就称为摄像机标定。本文选用棋盘格标定板作为靶标，并采用张正友标定法来实现摄像机内、外部参数的标定。该棋盘格标定板的方格数目为12×9，方格边长为9mm×9mm，精度为±0.001mm，方格的角点为特征点，在实际应用中具有角点易于提取、标定精度高、方向唯一等特点。

在标定过程中，保持传感器的内部结构和空间方位不变，接通激光器将十字线结构光投射到棋盘格标定板上。在摄像机的视野范围内自由地移动标定板，如图3所示。要始终保证十字线结构光投射在标定板上，并利用摄像机拍摄20幅不同位姿的有十字线结构光覆盖的标定板图像。为了减小随机误差以提高标定精度，标定板的位置应尽可能地分布在摄像机视场中的各个部分。

图3 标定过程Fig.3 Calibration procedure

提取出每幅标定板图像上的88个角点特征的亚像素级像素坐标，如图4所示，并应用与之对应的三维空间坐标以及张正友标定法进行求解，就可以完成摄像机标定。将世界坐标系OW-XWYWZW定义在第一幅标定板图像上，其原点OW设定在该图像左上角的第一个角点处，ZW轴设定为垂直于标定板平面并指向摄像机方向，XWOWYW平面设定为标定板平面。所得到的标定结果为：u0=1233.35，v0=972.83，fx=3801.37，fy=3789.34，

图4 提取矩形区域内的角点Fig.4 Extraction of the corners in the rectangular region

4.2 光条中心线提取

在实际应用中，由十字线激光器发射出的结构光，在本质上为两个连续且具有一定厚度的空间光平面，而在被测物体上所形成的具有一定宽度的投影光条特征，即为这两个光平面与物体表面相交而成的交线。一般说来，在该空间光平面的厚度方向上，光强近似服从高斯分布，因而在摄像机采集到的光条图像中，在沿着光条宽度的方向或光条的法线方向上，其灰度也会呈现出类似的高斯分布特点，即中心的灰度值大而边缘的灰度值小[9]，使得投影光条并非宽度为零的空间曲线，造成图像中的光条宽度不为单像素，这就给投影光条的准确定位带来了很大难题。

本文采用Steger方法来提取出投影光条的中心线，并以此作为十字线结构光的实际投射位置。该方法本质上属于拟合内插算法，其基本思路是首先通过Hessian矩阵获得光条的法线方向，然后在其法线方向上对像素灰度应用泰勒多项式展开而得到灰度分布函数，进而计算出光条中心的亚像素位置[10]。由于投影光条的灰度在其法线方向上近似为高斯分布，因而越靠近光条中心点的像素，其灰度值越大。因此，对该法线方向上的灰度分布函数的二阶泰勒多项式求取极值，即可得到光条在该法线方向上的中心点坐标。再由一系列的光条中心点依次连接而组成光条的中心线，从而完成光条中心线的提取与定位任务，如图5所示，所提取出的光条中心线分别记为L1和L2。在实际应用中，该方法具有较好的鲁棒性和通用性，而且能够达到亚像素级精度。

图5 光条中心线的提取结果Fig.5 Extraction results of the center lines of projection strips

4.3 结构光平面标定

确定两个光平面在世界坐标系OW-XWYWZW中的方程，就称为结构光平面标定。首先，提取出每幅标定板图像上的全部角点，并获取每个角点在图像像素坐标系o-uv中的二维坐标及其在世界坐标系OW-XWYWZW中的三维坐标，在o-uv中通过最小二乘法拟合出每一行角点所在直线的方程，如图6所示。一共可以得到8条拟合直线，分别记为直线1、直线2、…直线8。

图6 拟合每一行角点所在直线的方程Fig.6 Line equation of the corners of each row

然后，利用Steger方法分别提取出每幅标定板图像上的光条中心线在o-uv中的亚像素坐标，并应用最小二乘法分别拟合出两条中心线L1和L2所在直线的方程。最后，通过联立方程组分别求取出L1、L2与直线1～直线8的交点坐标，如图7所示。

图7 求取交点坐标Fig.7 Calculation of coordinates of the intersections

应用交比不变原理，即物方空间与像方空间的交比具有不变性，可以进一步计算出这些交点在OW-XWYWZW中的空间三维坐标。由于这些交点均位于各自的光平面上，因而可以作为光平面方程拟合的特征点，如图8所示。通过上述方法依次求取出每幅标定板图像上的光平面特征点，由这些特征点可以拟合出相应的光平面方程，图9为拟合出的两个光平面π1和π2。

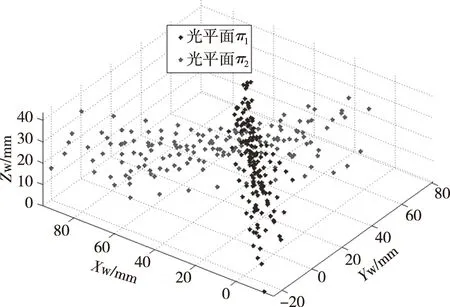
图8 光平面上的特征点Fig.8 Feature points on the structured light planes

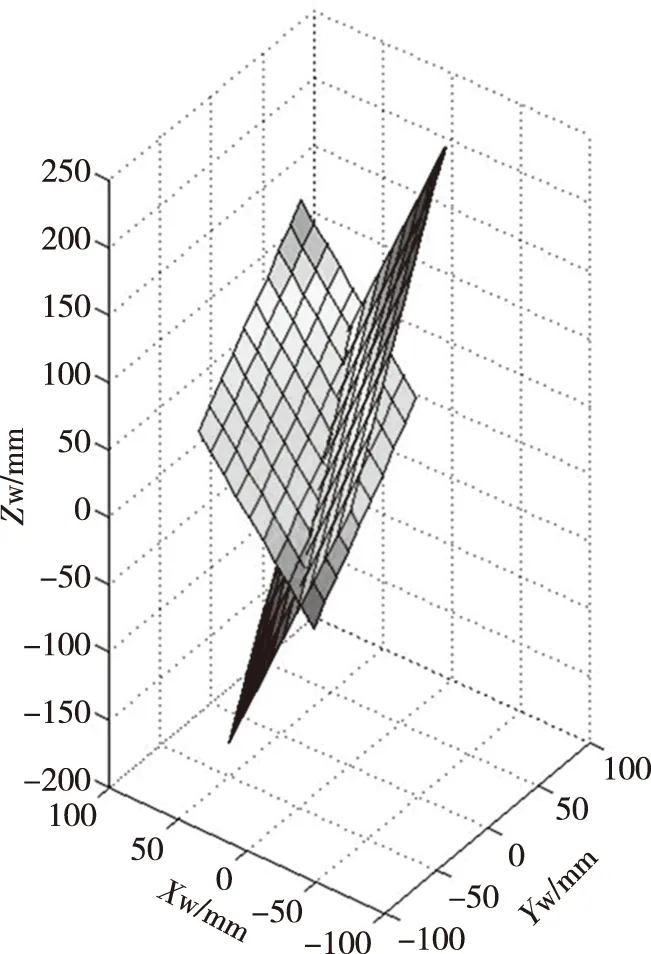
图9 拟合出的两个光平面Fig.9 Two fitted structured light planes

综上所述，本文通过棋盘格标定板实现了十字线结构光视觉传感器的结构参数标定，建立起了十字线结构光视觉传感器的数学模型

在此基础上，应用该传感器对被测物体进行扫描和测量时，由摄像机采集投射于物体表面上的投影光条图像，通过图像处理过程获取投影光条中心线上的像素点的图像像素坐标(u,v)，再通过公式(6)即可求取出与之对应的被测表面上采样点的世界坐标(XW,YW,ZW)。

5 试验验证

为了验证上述标定方法以及标定结果的有效性和正确性，本文应用该传感器开展飞机蒙皮上的铆钉孔钻孔点位处的法向矢量参数检测试验，试验现场如图10所示。在试验过程中，首先将十字线结构光投射在一个飞机蒙皮模拟样件的外表面上，并通过摄像机采集有投影光条覆盖的模拟样件图像，提取出其中的光条中心线L1和L2。然后，应用公式(6)和该传感器的结构参数标定结果，可以将L1和L2上的全部采样点的二维像素坐标(u,v)均转化为模拟样件表面上被测点的三维世界坐标(XW,YW,ZW)，如图11所示。从图11中可以看出，世界坐标系中的光条中心线保持了被测表面的连通性和拓扑性，从而真实地表征出被测物体表面轮廓的变化情况。

图10 试验现场Fig.10 Experimental scenes

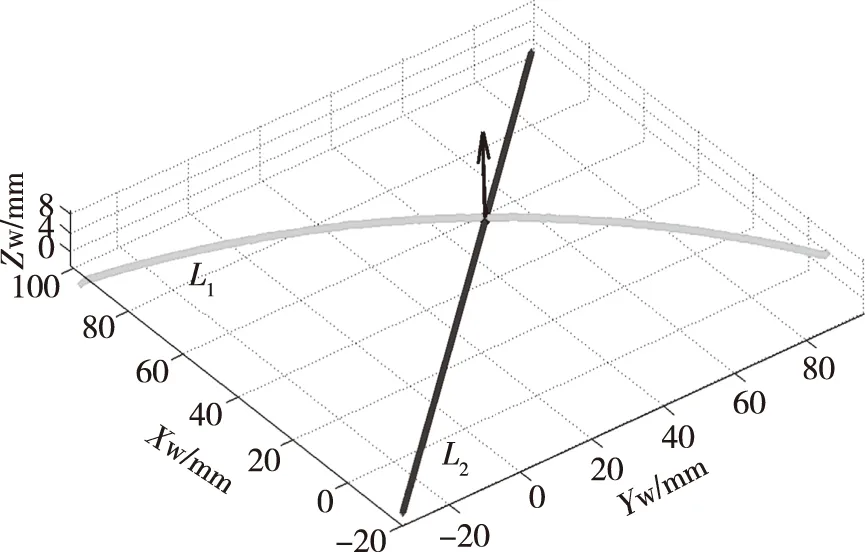
图11 世界坐标系中的光条中心线及法矢Fig.11 Center lines of projection strips and normal vector in the world coordinate system

采用二次曲线对光条中心线L1和L2上的采样点分别进行最小二乘拟合以得到L1和L2的参数方程，所获得的拟合优度R2=0.9968。根据L1和L2的参数方程进一步计算出投影光条中心点位处的法向矢量(l,m,n)，为了便于应用和表达，可以将计算出的法向矢量的各个分量l、m和n，分别转化为该点位处的法线方向与XW、YW和ZW轴之间的夹角α、β和γ。保持试验条件不变，连续进行10次重复性测量，所得结果如表1所示。

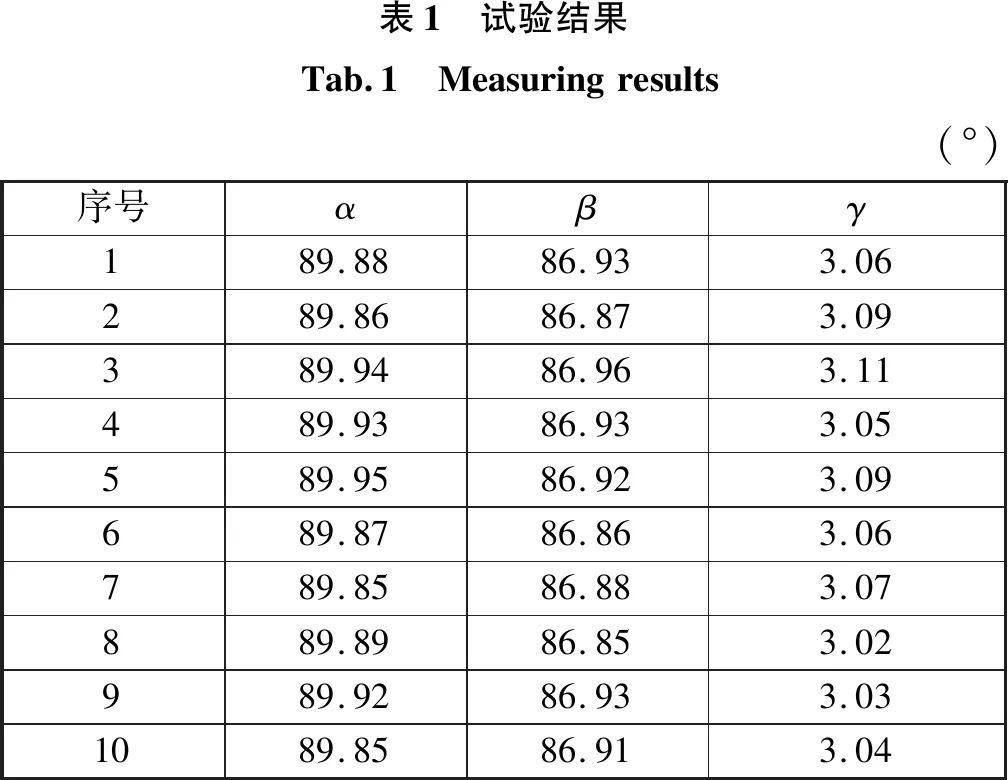
表1 试验结果Tab.1 Measuringresults (°)序号αβγ189.8886.933.06289.8686.873.09389.9486.963.11489.9386.933.05589.9586.923.09689.8786.863.06789.8586.883.07889.8986.853.02989.9286.933.031089.8586.913.04

6 结束语

本文开展了十字线结构光视觉传感器的结构参数标定方法研究，基于摄像机的成像模型建立了传感器的数学模型，并提出了传感器的结构参数标定方法。采用棋盘格标定板和张正友标定法获取了摄像机的内、外部参数；通过Steger方法完成了投影光条中心线的提取；并基于交比不变原理获取了光平面上的特征点，拟合出了结构光平面的方程，完成了传感器的结构参数标定，最后对标定结果进行了试验验证。试验结果表明，本文所提出的标定方法可以完成十字线结构光视觉传感器的参数标定，为该类型传感器的工程化应用奠定了坚实基础。