Fall cone tests considering water content, cone penetration index, and plasticity angle of fine-grained soils

Storu Shimobe, Giovnni Spgnoli

a College of Science and Technology, Nihon University, Funabashi, 274-8501, Japan

b BASF Construction Solutions GmbH, Dr.-Albert-Frank-Straße 32, Trostberg, 83308, Germany

Keywords:Atterberg limits Fall cone test Plasticity angle Water content Cone penetration index Plasticity ratio

A B S T R A C T This paper analyzed the consistency of some parameters of soils in the literature and experimental results from fall cone test and its application to soil plasticity classification. Over 500 data from both literatures and experiments using fall cone and Casagrande methods were compiled to assess the relationships among specified water content,cone penetration index（β）,and plasticity angle（α）of finegrained soils. The results indicate that no unique correlation exists among β, liquid limit of the fall cone test (LLc) and α. The water content at 1 mm cone penetration （C0） correlates well with β, plasticity ratio（Rp） (i.e. the ratio of plastic limit to liquid limit), and α. Finally, the potential of using the β-tan α diagram to classify soil plasticity was also discussed.

1. Introduction

Liquid limit (LL) of clays can be considered as the minimum water content at which the soil due to a small pressure (about 2-3 kPa) behaves as a viscous fluid (e.g. Carter and Bentley, 1991;Nagaraj and Miura, 2001). Plastic limit (PL) is the minimum water content at which soil can be deformed plastically without failing.The physical meaning of the Atterberg limits can be explained considering that the higher the water content of a soil,the less the interaction among contiguous particles, therefore the soil behaves as a liquid.However,in the case of a clayey soil,water adsorbed due to electro-chemical forces can exert high attractive forces; for determined water content, soil will not behave as a liquid. Higher liquid limit means that the water content under which the soil starts to behave as a liquid is higher.

Fall cone method is based on the measurement of penetration resistance of a cone by clay samples with different water contents.More specifically in the fall cone test, LL is the water content at which the clay sample is measured to sink for 20 mm in 5 s, by a conical tip of standardized angle(30°)and associated weight(80 g),according to the British Standard (BS) 1377-9 (British Standards Institution,1990); whereas in Sweden, the LL is determined for a cone with standardized angle of 60°and weight of 60 g,sinking in 10 mm (Swedish Standard, 1991). In this case, different cone geometries and weights are used in different standards(Shimobe and Spagnoli, 2019a).

In the past,several studies have been carried out using fall cone tests to determine Atterberg limits of cohesive soils(e.g.Wood and Wroth, 1978; Wasti and Bezirci, 1986; Feng, 2000; Koumoto and Houlsby, 2001; Sivakumar et al., 2009; Spagnoli, 2012; Di Matteo,2012), showing that LL of soil samples is determined more accurately by fall cone tests compared with that by Casagrande method,mainly due to errors of the operators and inaccurate assessment of the number of blows.

As for fall cone tests,the relationship between cone penetration（d） and water content （w） is given in terms of a power law over a wide range of water content (Shimobe, 2010; Shimobe and Spagnoli, 2019a) as

where C0is the water content at d=1 mm and β is the slope of the best-fitting line to the experimental points (hereinafter, the coefficient β is termed “cone penetration index”). The fall cone test,which is able to determine the liquid limit and plastic limit of soils simultaneously,is defined as the“extended fall cone test”(Shimobe and Spagnoli,2019a).The cone penetration index β is analogous to the“flow index”Ifin the Casagrande method,which is the slope of the w-log10N relationship, where N is the number of blows(Spagnoli et al., 2019). However, the mechanisms of the two methods are quite different (Nagaraj and Miura, 2001). Fig. 1 indicates an example of w-d relationships for natural soils. The natural soil 1 is volcanic cohesive soil (Kanto loam), natural soil 2 is volcanic organic soil (Kuroboku), natural soils A and B are construction generated soils, and artificial soils 1-6 are commercial clays used for pottery.

The validity of a linear log-log relationship expressed by Eq.(1)can be observed in Fig.1 over a wide range of cone penetrations and/or water contents. From Eq. (1) and Fig. 1, it shows that the coefficient β seems to depend on soil types (e.g. contents of clays and silts),while the constant C0(i.e.the water content measured at d=1 mm)depends on both soil and cone types(i.e.30°,80 g for BS and 60°,60 g for SS cones,respectively).The average value of β for fine-grained soils was considered to be 0.3 (Shimobe, 2000;Shimobe and Spagnoli, 2019a).

Considering cone penetration at the liquid limit(dLL)and plastic limit (dPL) of the Casagrande method, we know that dLL= 20 mm and dPL= 2 mm are used for the 30°, 80 g BS cone (i.e. Shimobe,2000; Feng, 2001). Then, fall cone liquid and plastic limits will respectively be

Taking into account the plasticity ratio, Rp= PL/LL (Shimobe and Spagnoli, 2019b), we have

where Rpcis the plasticity ratio for fall cone tests. The following expression is valid for the SS cone when considering the general trend where the undrained shear strength suat LL and PL generally match the following relationship,su(PL)≃100su(LL)(Skempton and Northey,1952; Sharma and Bora, 2003). On the Casagrande plasticity chart (the relationship between Ipand LL, where Ipis the plasticity index of clays), the plasticity index for fall cone method(Ipc) is

Eq. (5) is the direct proportion expression of the Ipc-LLcrelationship with the slope A. Therefore,we have

It is possible to observe that Ipc/LLcis a function of cone penetration index β only. The average value of β is 0.3 as suggested by Shimobe and Spagnoli(2019a).The aim of this study is to interpret and assess other index parameters(e.g.β and C0)for soils based on the extended fall cone method and the potential of effectively utilizing β to classify soil plasticity, which differs from previous researches. Another aspect that has not yet been addressed is the soil plasticity classification using LLcand Ipcconsidering the plasticity angle (α), suggested by McNaab (1979) and Rao (1996), as additional indices in conjunction with the coefficients β and C0:

The plasticity angle （α） is related to the A-line intercept and represents a measure of divergence from the A-line, as soils with value tan α = 0.73(i.e.α = 36.1°)are on the A-line and soils with value tan α ＞0.73 (i.e.α ＞36.1°) have a higher plasticity.

This paper re-visits the aforementioned consistency index parameters of soils by the extended fall cone method and its application to soil plasticity classification. Herein, data from over 40 studies and experimental tests on 121 soils are compiled to investigate the relationships among α（tanα）, β, C0and Rp. Finally, potential application of using the β-tan α diagram to soil plasticity classification is discussed.

Fig.1. Relationship between the water content (w) and cone penetration (d) of fine-grained soils by the extended fall cone test.

2. Methods

Over 40 publications were evaluated and analyzed in this work.In order to provide a comprehensive overview,search engines,such as Google Scholar, Scopus, complemented with Springer Link,Taylor & Francis Online and ResearchGate platforms, were used.Journal and conference papers as well as symposium papers, academic lectures, thesis dissertations were screened. Neither language nor publication date limits were set, in order to provide a broad overview on this topic.The keywords were clays,liquid limit,Casagrande, fall cone, plastic limit, liquid limit, and correlations.Besides, tests from the authors were also presented. The geotechnical properties of 121 different fine-grained soils were tested according to the Japanese Industrial Standards (2009a,b, 2020).

3. Results and discussion

Eq.(1)correlates water content with cone penetration in terms of a power law.For this,the relationships among the water content（C0）at d = 1 mm,cone penetration index（β）,plasticity ratio（Rp）,and plasticity angle（α）were plotted with 500 data.Besides,β was also plotted against Rp, LLc, and α. Meanwhile, relationships considering the Casagrande plasticity chart were also obtained. In the legends of Figs.2-8,“several other researchers”is referred to as the papers from Arasan and Yetimoˇglu(2008),Arifin(2008),Chinn and Pillai (2008), Dolinar (2009), Grabowska-Olszewska (2003),Hobson (2008), Monkul and Ozden (2007), Sankara (2006),Sridharan et al.(1999),Viladesau Franquesa(2004),and Wang et al.(2012).

3.1. Relationship between C0 and β

Fig.2 shows the C0-β relationship of various soils with a wide range of plasticity based on 30°, 80 g BS cone tests. Besides, the conventional soil classification labels (CH-heavy clay, CL-lean clay,MH-heavy silt,ML-lean silt)are also indicated near the data points for reference(after this,similarly).Over 400 data were used in Fig. 2. It can be observed from Fig. 2 that C0increases with the decrease in β.This is the reason why the cone penetration index β increases in general with increase in plasticity, and vice versa. C0decreases due to the largely reduced change in logarithmic water content （Δlog10w） against the change in the logarithm of cone penetration （Δlog10d）. Besides, the proposed model (i.e. Eq. (8)) is shown in Fig.2(solid line in red)that is determined by combination of Eqs.(9)and(10),based on previous cohesive soils data(Shimobe and Miyamori,1996). The relation is described as

3.2. Relationship between C0 and Rp

The C0-Rprelationship is shown in Fig.3.Over 400 data of Rpby the Casagrande method were collected and are plotted in Fig.3.It can be seen in this figure that the plots are more scattered in comparison with those in Fig.2.However,it still clearly shows that C0increases with increase in Rp.As a rough estimate,the Rp= 0.27 line (dashed line in pink) related to the slope of A-line on Casagrande plasticity chart,and the regression curve(solid line in blue;see Eq.(9)from Shimobe and Miyamori,1996)were inserted in the figure. When Rp<0.27, the values of C0become smaller, which corresponds to high-plasticity soils, e.g. bentonites.

3.3. Relationship between C0 and α

Fig.2. Relationship between C0 and cone penetration index（β）by the extended fall cone method,considering new authors’data,as well as data of Barnes(2009),Lee and Freeman(2007,2009),Zentar et al.(2009a,b),Rashid et al.(2008),Clayton et al.(2008),Stone and Kyambadde(2007),Orhan et al.(2006),Mahajan and Budhu(2006),Kodikara et al.(2006),Molenaar(2005),Huang(2005),Dolinar and Trauner(2005),Feng(2000,2001,2004,2005),Li(2004),Sridharan et al.(1999,2000),Kumar and Wood(1999),Sridharan and Nagaraj(1999), Campos et al. (1999), Smith and Smith (1998), Yudhbir (1991), Harison (1988), Wasti and Bezirci (1986), Wood (1985), Allbrook (1980).

Fig.3. Relationship between C0 and plasticity ratio（Rp）,considering new authors’data, as well as data of Zentar et al.(2009a,b),Orhan et al.(2006),Li(2004),Kumar and Wood(1999), Smith and Smith (1998), Wasti and Bezirci(1986), Barnes (2009),Rashid et al. (2008),Huang (2005), Feng(2000, 2001,2004,2005),Campos et al. (1999), Yudhbir (1991),Wood (1985), Lee and Freeman (2007, 2009), Clayton et al. (2008), Sridharan et al. (1999, 2000), Harison (1988).

Fig.4. Relationship between C0 and tangent of plasticity angle（tanα）considering new authors’data, as well as data of Barnes (2009),Lee and Freeman(2007,2009),Zentar et al.(2009a, b), Rashid et al. (2008), Clayton et al. (2008), Huang (2005), Feng(2000, 2001, 2004, 2005), Panayiotopoulos et al. (2004), Li (2004), Sridharan et al. (1999), Campos et al.(1999), Yudhbir (1991), Jacquet (1990), Wood (1985).

Fig.4 shows that C0decreases with increasing tanα determined by the Casagrande’s procedure. Here, the line tanα = 0.73 (solid line in red) equaling to the gradient of A-line on plasticity chart was inserted as a characteristic line for soil classification. When tan α ＞0.73, data of the clay types, i.e. CH and CL, were plotted with a constant trend;while tan α<0.73,data of the silt types,i.e.MH and ML, are more scattered. These trends are shown in also Fig. 3

3.4. Relationship between β and plasticity ratio Rp

Fig. 5 shows the relationship between the cone penetration index β and plasticity ratio Rp,including Rpcfor fall cone tests.Here,the regression curve in Eq.(10)(Shimobe and Miyamori,1996;red solid line in Fig. 5) obtained using the authors’ data was indicated together with Eq.(11)(Mesri and Peck,2011;blue point-dotted line in Fig. 5).

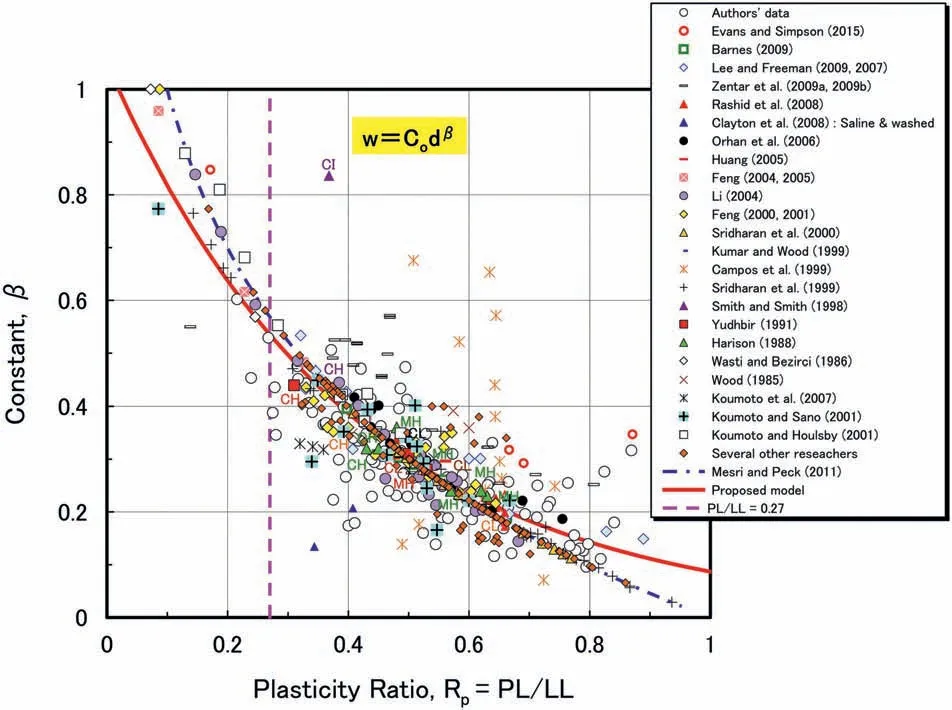
Fig. 5. Relationship between β and plasticity ratio Rp considering new authors’ data, as well as data of Evans and Simpson (2015), Barnes (2009), Lee and Freeman (2007, 2009),Zentar et al.(2009a,b),Rashid et al.(2008),Clayton et al.(2008),Orhan et al.(2006),Huang(2005),Feng(2000,2001,2004,2005),Sridharan et al.(1999,2000),Kumar and Wood(1999), Campos et al. (1999), Smith and Smith (1998), Yudhbir (1991), Harison (1988), Wasti and Bezirci (1986), Wood (1985), Koumoto and Houlsby (2001), Koumoto and Sano(2001), Koumoto et al. (2007), Mesri and Peck (2011).

Fig. 6. Relationship between β and fall cone liquid limit LLc considering new authors’ data, as well as data of Zentar et al. (2009a, b), Mahajan and Budhu (2006), Moon and Jayawardane (2004), Feng (2000, 2001, 2004), Yudhbir (1991), Wood (1985), Campbell (1975), Barnes (2009), Rashid et al. (2008), Kodikara et al. (2006), Sridharan and Nagaraj(1999), Harison (1988), Sampson and Netterberg (1985), Sherwood and Ryley (1970), Koumoto et al. (2007), Lee and Freeman (2007, 2009), Clayton et al. (2008), Dolinar and Trauner (2005), Li (2004), Sridharan et al. (1999), Wasti and Bezirci (1986), Allbrook (1980), Koumoto and Houlsby (2001), Shimobe and Miyamori (1996).

Using the values of Rpc,Eq.(11)would match with the fall cone experimental data. Based on the values of Rpdetermined by the Casagrande method,it can be seen from Fig.5 that although there is a difference between Eqs. (10) and (11), both equations can well explain the trend of experimental data comparatively, with some exceptions. Besides, most of data related to “several other researchers”(in the legend of Fig.5)fall precisely on the line plotted by Eq. (11).

3.5. Relationship between β and the fall cone liquid limit LLc

Fig.6 shows the relationship between β and fall cone liquid limit LLc. Here, the 30°fall cone data with different weights are summarized for various soils with a wide range of plasticity.These data are also compared with the average trend lines (upper and lower lines)suggested by Mesri and Peck(2011; see Eq.(11)).Besides,in the 30°,100 g cone tests,the values of LLcwere determined by the corresponding cone penetration at dLL=22.4 mm(Shimobe,2000,2010). It can be seen from Fig. 6 that the values of β generally increase with the increase in LLc,except for some soil types.Based on the entire fall cone data, however, a unique empirical relationship for β does not exist.Such an experimental evidence is as well as the result from Mesri and Peck (2011) using the values of LL and PL determined by the Casagrande method.

3.6. Relationship between β and the plasticity angle α

Fig. 7 shows the relationship between β and α. In order to identify and classify the soils with different plasticity indices in terms of β and tan α，the two characteristic lines(tan α = 0.73 and β = 0.3) are provisionally inserted in this figure. Also, the conventional soil classification labels (CH, CL and MH, ML) are indicated near the data points. Besides, the tanα = 0.73 line with the same slope as the A-line on Casagrande plasticity chart differentiates clays from silts.The β = 0.3 line considered from the aspect of mechanical cone penetration-water content behavior obtained by the extended fall cone method may be used as measures for identifying the approximate boundary between clays and silts.Moreno-Maroto and Alonso-Azcárate (2017) proposed a new soil classification chart with the two characteristic lines named“C-line”and “M-line” based on their soil thread-bending test results. The two new lines introduced to separate clays and silts,i.e. the C-line(for clays) and the M-line (for silts), correspond to the ratios Ip/LL = 0.4855 and 0.3311, respectively. These ratios refer to as the slopes in those relationships between Ipand LL. According to Eq.(6),the values of β corresponding to the ratios mentioned above are obtained as β = 0.29 in the C-line and β = 0.17 in the M-line.Especially,the value of β in C-line is very close to the characteristic line β = 0.3 in Fig. 7. These interpretations are shown together with fall cone data (LLc< 250%) in Fig. 8. Besides, the upper and lower limits of β for natural and artificial soils, except that of β for high-plasticity/compressibility soils (e.g. Na-bentonite), were considered as 0.8 and 0.1,respectively,in Fig.2.In Fig.8,it is worth noticing that both limits of β match well with the experimental data. The soils with intermediate features between clays and silts are located in the area between the C-line and the M-line (i.e. CLML and CH-MH groups; see Moreno-Maroto and Alonso-Azcárate,2017). In addition, the value of β seems to increase with increasing fall cone liquid limit (LLc) and/or the fall cone plasticity index （Ipc）, see Fig. 6 and Eq. (6). Finally, all the data are roughly separated into the four categories by the tan α = 0.73 and β = 0.3 lines in Fig. 7. Further investigations are needed to identify the characteristics of each category.

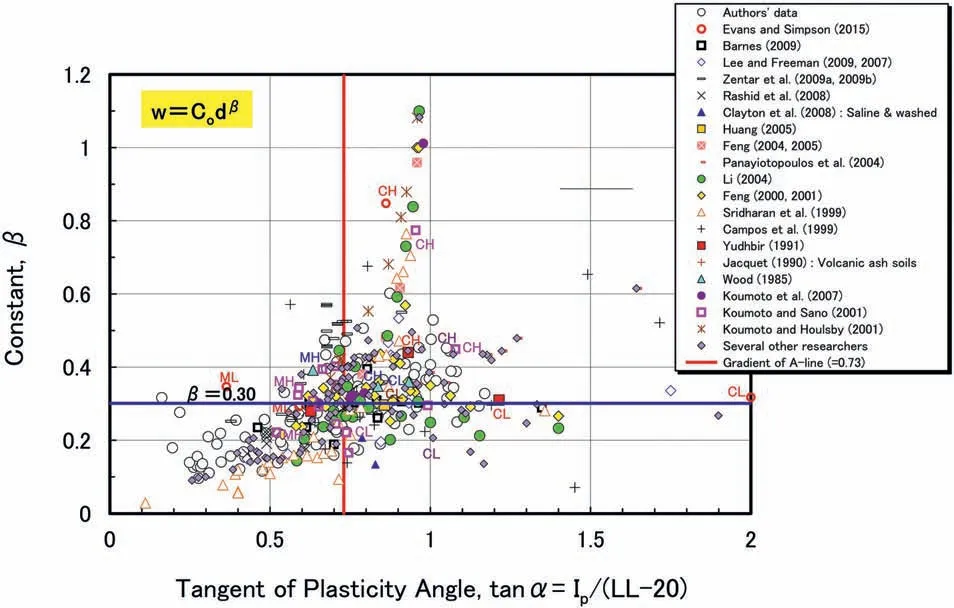
Fig.7. Relationship between β and tangent of plasticity angle （tanα） considering new authors’data, as well as data of Evans and Simpson(2015),Barnes (2009),Lee and Freeman(2007, 2009), Zentar et al. (2009a, b), Rashid et al. (2008), Clayton et al. (2008), Huang (2005), Feng (2000, 2001, 2004, 2005), Panayiotopoulos et al. (2004), Li (2004), Sridharan et al. (1999), Campos et al. (1999), Yudhbir (1991), Jacquet (1990), Wood (1985), Koumoto et al. (2007), Koumoto and Sano (2001), Koumoto and Houlsby (2001).

Fig. 8. Plasticity chart determined from extended fall cone method (LLc < 250%) considering new authors’ data, as well as data of Mahajan and Budhu (2006), Feng (2000, 2001,2004,2005),Sridharan et al.(1999),Wasti and Bezirci(1986),Lee and Freeman(2007,2009),Huang(2005),Li(2004),Smith and Smith(1998),Wood(1985),Zentar et al.(2009a,b),Dolinar and Trauner (2005), Yudhbir (1991), Allbrook (1980), Rashid et al. (2008), Campos et al. (1999), Harison (1988).

On the other hand,the need of a new soil classification based on the value LLcis needed to compare with the conventional Casagrande plasticity chart (see Fig. 8). As reported by Di Matteo et al.(2016), the use of LLcinstead of Casagrande LL may change the suitability of the same soil in earthwork applications. Since those experimental data are widely or partially scattered, the proposed correlations may not be effective as a substitute of the soil laboratory test without certain theoretical support. However, it would be useful for a preliminary geotechnical estimate, when other parameters are already available. The essential purpose of the proposed empirical relationships is to understand whether one parameter can depend on another, considering the increasing interest and use of the empirical relationships in the professional geotechnical field.

4. Conclusions

This paper tried to consider the consistency index parameters(β and C0)of soils by the extended fall cone method,with possibility of application to soil plasticity classification. Over 500 data, from literatures and experiments,were used to assess fine-grained soils in terms of the relationships amongst specified water content, cone penetration index β, and plasticity angle α. The relationship between the specified water content （C0） at 1 mm cone penetration and cone penetration index β over a wide range of plasticity shows that C0increases with decrease in β.A C0-β model was obtained,which links the relationships of these two factors with the plasticity ratio Rp（Rp= PL/LL）. C0was plotted against Rpand it increases with increasing Rp. Plotting C0against the tangent of plasticity angle(i.e.tan α),it can be observed that C0decreases with increase in tanα, especially for high-plasticity clays. The cone penetration index β was plotted against the plasticity ratio Rpas well, and a β-Rpmodel was compared with that developed by Mesri and Peck(2011),which shows a good match.The correlation between β and liquid limit of the fall cone test LLcindicates that a unique empirical relationship does not exist. Concerning the relationship between β the plasticity angle α, two characteristic lines,tanα = 0.73 and β=0.3,were used to separate clays and silts.The plotted data were roughly identified in four different areas. However, further investigations are needed.

Declaration of competing interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

List of symbols

w Water content(%)

C0Water content measured at d = 1 mm (%)

d Cone penetration (mm)

dLLCone penetration at liquid limit (mm)

dPLCone penetration at plastic limit (mm)

IpPlasticity index, which equals LL- PL

IpcPlasticity index obtained from fall cone test

IfFlow index (%)

LL Liquid limit (%)

LLcLiquid limit obtained from fall cone test (%)

N Number of blows

PL Plastic limit (%)

PLcPlastic limit obtained from fall cone test(%)

RpPlasticity ratio

RpcPlasticity ratio obtained from fall cone test

suUndrained shear strength (kPa)