Micro-annulus generation under downhole conditions: Insights from three-dimensional staged finite element analysis of cement hardening and wellbore operations

Weicheng Zhang, Andreas Eckert

Department of Geosciences and Geological and Petroleum Engineering, Missouri University of Science and Technology, Rolla, MO, USA

Keywords:Micro-annulus Debonding Staged finite element analysis Cement hardening Poro-elastic bulk shrinkage Pore pressure Temperature fluctuation

A B S T R A C T A micro-annulus (MA) is defined as a high permeability zone or gap initiating/occurring at the casingcement and cement-formation interfaces during the wellbore life span. An MA can significantly compromise wellbore integrity by establishing enhanced fluid flow pathways. This study uses a staged finite element approach to simulate wellbore integrity during various loading steps of wellbore operations under downhole conditions. Particular emphasis is placed on the processes of cement poro-elastic property evolution, volume variation, and pore pressure variation as part of the cement hardening step.The resulting state of stress during the life cycle of a typical injection well (i.e. hardening, completion,and injection) is analyzed to assess the onset and evolution of micro-annuli at various interfaces of the composite wellbore system under downhole conditions. The results show that cement shear failure is observed at the casing-cement interface during pressure testing (excessive wellbore pressure); and tensile debonding failure initiates at the cement-formation interface due to cement shrinkage during hardening and injection-related cooling (thermal cycling). Sensitivity analyses considering several parameters show that: (1) the degree of poro-elastic bulk shrinkage has significant implications for both shear and tensile failure initiation - the less the cement shrinks, the less likely the failure initiation is;(2)cement integrity increases with increasing depth;(3)cement pore pressure evolution has significant implications for tensile failure-if cement pore pressure decreases more,higher temperature differences can be sustained before an MA occurs; and (4) cement temperature fluctuations during hardening promote initiation of debonding failure. In summary, the results presented indicate that establishing downhole conditions to quantitatively analyze MA generation is necessary. The results are different compared to laboratory studies without considering/simulating downhole conditions. The knowledge from this study can raise the awareness of predicting and evaluating MA under downhole conditions and can be used to supplement and improve future laboratory experiments.

1. Introduction

Inter-zonal communication in the wellbore is a challenging issue as the unwanted migration of formation fluids along the wellbore can lead to reduction of production/injection efficiency,contamination of fresh water aquifers during wastewater disposal,CO2sequestration, and old well abandonment (Celia et al., 2005).Various factors, including poor cement job quality, incompatible cement-slurry design, and drastic wellbore temperature/pressure changes (Bois et al., 2011), arising during the life cycle of the wellbore, may compromise the integrity of the cement sheath individually or cumulatively and result in loss of zonal isolation. A thorough and integrated mechanical analysis of the composite wellbore system (i.e. casing-cement-formation) is required to understand and predict the interactions of different components and the corresponding likelihood of cement failure (Lavrov and Torsæter, 2016).

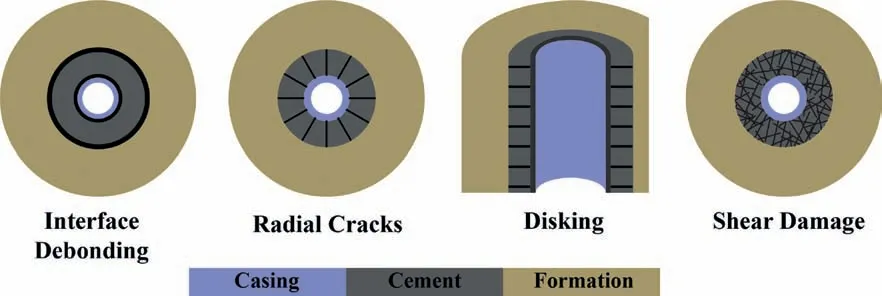
Fig.1. Four types of cement failure (adapted from Bois et al., 2011).

Bois et al. (2011) summarized the failure of cement sheath into four types (Fig. 1). Among the three types of tensile failure, systematic and inter-connecting debonding fractures at the casingcement and the cement-formation interfaces (Fig.1a) can be classified as a micro-annulus (MA), which initiates when the radial stress equals the tensile strength (Lavrov and Torsæter, 2016). Under certain loading conditions,an MA at the cement-casing and the cement-formation interfaces may have large apertures (say 10-100 μm) to act as a fluid flow channel (Stormont et al., 2018), and may propagate to connect different zones. The three major factors that can promote the generation of an MA are(Nelson and Guillot,2006;Bois et al.,2012;Lavrov and Torsæter,2016):(1)mechanical loads due to pressure variations after wait on cement; (2) thermal stresses arising from temperature differences between an injection fluid and the formation; and (3) cement shrinkage during hardening.

The first two factors have been extensively studied using laboratory experiments following two major approaches:(1)Cement is cured in the annulus between two confining sets of casings and a testing pressure is applied on the inner casing after the cement is cured (Goodwin and Crook, 1992; Jackson and Murphey, 1993;Therond et al., 2017). These studies observed that, when a high inner casing pressure is removed or reduced, annular leakage occurs.An MA at the inner-casing to cement interface is predominant for low compressional strength cement, while radial cracks are predominant for high compressional strength cement. Boukhelifa et al. (2005) observed that after several loading-unloading cycles, an MA occurs at the cement-outer casing interface for expanding cement systems, and both MA and radial cracks for cement systems shrink during hardening.(2)The second approach includes a rock ring to represent the formation and the entire system is contained in a pressure vessel allowing investigation of MA generation during both pressure testing and thermal cycling.De Andrade et al. (2015) observed that after thermal cycling using extreme temperature differences (140°C), severe interface debonding at both the casing-cement and cement-formation interfaces occurs, if the cement is cured without pressure; while no debonding is observed, if the cement is cured under pressure. In summary,while these laboratory studies inherently account for the occurrence of cement hydration and shrinkage,they also show that the occurrence and location of MA are highly dependent on the individual experimental setup. Moreover, quantifying the exact timing,stress conditions,and which physical process is responsible for the initiation of an MA remains a challenge. Key aspects of simulating downhole conditions, and how the addition of the stressed formation surrounding the cased cement sheath and the existence of pore fluid pressure in the formation and the cement affect the location, likelihood of occurrence, and aperture of the observed MA, need further investigation.

During cement hardening, the processes associated with cement hydration reaction (during which the cement consumes water, generates porous skeleton and pore pressure, shrinks as it transforms from a fluid into a solid,develops strength,adheres with casing and formation rock, and becomes an impermeable barrier(Nelson and Guillot, 2006)) are the most complex, and therefore most challenging to be included in an integrated fashion in either laboratory or numerical experiment. The process during cement hardening with the most significant influence on the mechanical response and associated cement failure is shrinkage (e.g. Lavrov and Torsæter, 2016). To quantify the influence of shrinkage, it is necessary to correlate and integrate the evolution of shrinkage with development of the cement mechanical properties, preferably under appropriate downhole conditions accounting for temperature(Backe et al.,1999),pressure(Reddy et al.,2009),and water supply(Appleby and Wilson,1996).Bois et al.(2011,2012,2019)developed a coupled poro-chemo-thermo-mechanical model to describe the mechanical response(as a function of the hydration reaction)of the wellbore system to external loads during cement hardening. Their results indicate that excessive casing pressure induces localized cement shear failure at the casing-cement interface. MA due to cement pore pressure reduction during hardening may result in debonding at both interfaces,but also depend on the interaction of the poro-elastic parameters of the cement and formation;MA due to injection-related cooling is likely to occur at the casing-cement interface.

‘Staged’ finite element analysis (FEA) is considered as an efficient alternative approach to simulate the mechanical response of a composite wellbore system. In particular, how the various loads during the life cycle of the well affect cement failure under in situ conditions is of interest (e.g. Bosma et al.,1999; Ravi et al., 2002;Gray et al., 2009; Nygaard et al., 2014; Li and Nygaard, 2017; Orlic et al., 2018; Zhang and Eckert, 2018). In general, these numerical studies are in agreement that an MA due to excessive inner casing pressure occurs at the casing-cement interface; an MA due to cement shrinkage and injection-related cooling(thermal cycling)is generated at the cement-formation interface. The pore pressure magnitude in the cement, the cement mechanical properties, the formation rock properties,and in situ stress regime have significant influences on MA generation and the resulting aperture. One common assumption in all numerical simulations is the state of stress of the cement during hardening. End member cases include zero effective stress (i.e. hydrostatic slurry pressure; Bosma et al.,1999; Ravi et al., 2002; Gray et al., 2009) and a finite, compressive effective stress given by the difference between slurry pressure and hydrostatic pore pressure (Gray et al., 2009; Nygaard et al.,2014; Li and Nygaard, 2017). While the latter studies assume a finite effective stress in the cement after the hardening stage(i.e.by applying a finite pressure load),which has been shown to improve cement bond quality(De Andrade et al.,2015),these studies do not physically account for the pore pressure in the system (Nygaard et al., 2014; Li and Nygaard, 2017). Moreover, a detailed analysis accounting for the evolution of mechanical properties during cement hardening and their influence on the cement state of stress,as suggested by Bois et al. (2012, 2019), is missing.

The objective of this study is to present a staged threedimensional (3D) FEA modeling approach that enables to simulate the complete load cycle during the entire wellbore life span.The approach integrates the effects of in situ loads (i.e. downhole conditions of stress, pore pressure, wellbore pressure, and temperature), cement hardening, failure characterization (including shear and tensile failure) accounting for the bulk poro-elastic properties of the formation, cement and interface interactions(i.e. bond strength, friction, post-failure evolution of debonding fractures), as well as major wellbore construction, completion,testing and production loads (i.e. injection, thermal cycling). In difference to other staged FEA studies, this approach accounts for the multiple physical processes during cement hardening, such as the development of the cement poro-elastic properties, bulk shrinkage, pore pressure, and temperature fluctuations during the hydration reaction and associated thermal stress(Bois et al.,2012).Based on the resulting state of stress developed during the various stages modeled, this study quantitatively analyzed the conditions and locations of MA initiation and resulting MA aperture. Critical information such as the temporal evolution of MA and the accumulated influence by loads from multiple operations and procedures can be provided and the risk evaluation for MA occurrence is presented based on quantitative results.

2. Methodology

2.1. Model setup

2.1.1. Model geometry and material properties

Fig. 2. Illustration of the modeling domain of this study and the model geometry adopted from the cased wellbore section.

In this study,numerical models representing the central section of a cased borehole(i.e.above the bottom hole assembly;Fig.2)are simulated using the commercial finite element software package Abaqus™(SIMULIA, 2017). Due to symmetry conditions and to improve numerical efficiency, only a quarter representation of the wellbore is simulated.The model domain includes a 5.5.in.casing(124.26 mm in inner diameter and 139.7 mm in outer diameter),cement sheath, and a formation component with a 7.875 in.borehole (200.03 mm in diameter; Fig. 2). Cement and formation components are simulated as poro-elasto-plastic materials with thermal and pore pressure properties,and the casing is modeled as a linearly elastic material(Table 1).Interface bonds using cohesive contact behavior governed by a quadratic traction-separation law(SIMULIA,2017)are inserted between casing-cement and cementformation components (Table A1 in Appendix A), and is explained in detail in Appendix A. Several scenarios are investigated and analyzed in this study in order to better understand the influence of several major factors that occur during cement hardening and the influence of operation related loads after cementing.

2.1.2. Loading steps for the staged FEA approach

The staged FEA approach of this study includes six loading steps,which are based on the general stages during the life span of an injection well (Fig. 3). For various depths tested, in situ stresses,pore pressure, mud pressure, cement slurry pressure, testing pressure, and fluid injection pressure are listed in Table 2. A static pre-stressing loading step to obtain an equilibrated gravitationalloaded state of stress is applied before drilling (e.g. Eckert and Liu, 2014; Eckert and Zhang, 2016).

(1)Step 1: Pre-stressing.An exemplary extensional stress regime, with equal effective maximum and minimum horizontal stressesand an effective horizontaland verticalstress relationship ofare applied. The pore pressure in the model domain is set to be uniform and hydrostatic.

(2)Step 2: Drilling.A cylindrical volume of rock is removed from the borehole location and a uniform mud pressure is applied on the surface of the borehole wall.

(3)Step 3a:Casing.Casing elements are introduced.Equal mud pressures are applied on the inner and outer casing walls.Step 3b:Cementing.A cement slurry pressure is applied on the inner wall of the formation and outer wall of the casing to represent the fluid pressure from the cement slurry column.The cement elements are added to the model. The inner surface of the casing is still loaded with the mud pressure.

(4)Step 4:Cement hardening.An initial state of stress equal to the hydrostatic pressure of the cement slurry minus the pore pressure is applied to the cement. Then the cement shrinks volumetrically as the cement develops the poro-elastic properties during the transition from an immobile viscoelastic solid to a poro-elastic solid. This process is described in detail in Section 2.2.2.

(5)Step 5a: Pressure testing.This step represents the pressure variation at the inner casing during a leak-off test. The pressure assigned at the inner casing increases until any type of failure is observed. The maximum pressure that the system can withstand without failure is recorded.Step 5b:Completion.The mud pressure applied to the inner casing is replaced with completion fluid pressure, which equals the hydrostatic pore pressure (Bellarby, 2009). A time period of 5 min is assigned for this step.

(6)Step 6: Injection.The entire model is exposed to a uniform formation temperature(45°C) at the beginning of this step,which includes two processes (Economides et al., 2012):

(a) Charging process:the injection pressure load is increased from hydrostatic pressure to the designed injection pressure (from 5 min to 15 min) and a temperature boundary condition of 15°C is applied on the inner casing at a rate of 3°C/min. The linear temperature reduction is an approximated simplification of the heatconvection process (Ali,1981) and is widely used in the other similar numerical studies (e.g. Li and Nygaard,2017; Roy et al.,2016).

Table 1 Material properties for the casing,cement,and formation components.Casing material properties are adapted from Roy et al.(2016).Cement is assumed to be Portland Class G cement and is adapted from Philippacopoulos and Berndt (2001). Formation rock is assumed to be sandstone and both cement and sandstone properties are adapted from Busetti et al.(2012)and Roy et al.(2016).Thermal properties are adapted from Roy et al.(2016).ρ:density;E:Young’s modulus;ν:Poisson’s ratio;k:permeability;φ:porosity;ψ: dilation angle;β: angle of friction;λ: thermal conductivity; c: specific heat;α: thermal expansion coefficient.

Fig. 3. Loading steps of the multi-staged FEA approach to simulate downhole conditions.

(b) Plateau process: the injection temperature and pressure are maintained over a designated injection period(40 h).

The six loading steps represent a common multi-staged modeling setup (Ravi et al., 2002; Gray et al., 2009; Nygaard et al., 2014; Feng et al., 2016). An MA generated is assumed to have perfect thermal conductivity with no fluid invasion. Table 3 lists the base case and sensitivity analysis scenarios for factors related to cement hardening, and also presents the ‘pressure testing’ and ‘injection’ steps that are performed after the ‘cement hardening’ step for all scenarios occurring at Step 4.

2.2. Simulation of cement hardening

In order to simulate a representative evolution of the effective state of stress in the cement during the hardening process, the volume variation, poro-elastic property evolution, and pore pressure evolution during the cement hydration are the essential physical processes that have to be accounted for (Bois et al., 2012;Samudio,2017).For the simulations presented,the time span of the cement hardening is assigned to be 48 h,which is a normal wait on cement (WOC) time and the testing time for most experimental studies (Bourissai et al., 2013; Samudio, 2017). During this period,the cement slurry transfers into a poro-elastic solid and the state of stress is established.Hence,input parameters for this time span are collected from experimental and theoretical studies performed under conditions that are similar to the downhole conditions simulated in this study.

2.2.1. Numerical characterization of cement shrinkage

The volume variation of the cement system (shrinkage) is the result of multiple chemical,physical,and mechanical processes that are associated with the hydration reaction. In terms of the mechanical influence of shrinkage, numerical investigations of Thiercelin et al.(1998),Bois et al.(2011,2012)and Zhang and Eckert(2018) proposed that the bulk shrinkage measured as the external volume reduction cannot have a 100% elastic response to the system. Otherwise radial and circumferential fractures would inevitably occur in the cement during hardening, which is also not observed in laboratory studies(Nelson and Guillot,2006).Previous numerical studies either simulate the shrinkage as an instantaneous process by applying the final elastic properties of the solid cement and the resulting state of stress and pore pressure (Gray et al., 2009; Li and Nygaard, 2017; Orlic et al., 2018), or simulate the cement volume variation after the cement is set (Ravi et al.,2002). Since a continuum mechanics based finite element approach is utilized, the key assumption to simulate the bulk shrinkage numerically is that various physical and chemical processes of hydration reaction(during hardening)can be represented by the mechanical processes,and hence can be modeled as a poroelastic bulk shrinkage process. Several assumptions are necessary for this approach:

Table 2 Input parameters for the staged FEA approach of this study. The in situ stresses are given in total stresses.

Table 3 Staged downhole condition scenarios (SDCS) investigated in this study.

(1) Poro-elastic bulk shrinkage is assumed to start when the cement completely loses its mobility (～10 h, at the end of the initial setting period or the beginning of the hardening period).By this time,the cement permeability becomes very low and the pore pressure starts to decrease (Appleby and Wilson, 1996; Kurdowski, 2014; Zhang et al., 2017). All the shrinkage prior to the cement being immobile is assumed to be zero, since the volume variation can be compensated by the flow of the slurry.

(2) A compressive effective state of stress (equal to the cement slurry pressure minus the hydrostatic pore pressure) is applied as the initial state of stress for the cement.

(3) A certain portion of the bulk shrinkage is assumed to have a poro-elastic response. Initially, the bulk shrinkage data(Fig.4)from Chenevert and Shrestha(1991)are multiplied by the ratio, s (termed poro-elastic bulk shrinkage coefficient;Table 2 and Fig. 4). An estimate of 50% is assumed initially and sensitivity analyses are performed (see Table 2) to determine a representative ratio between poro-elastic bulk shrinkage and bulk shrinkage (see Section 5). Future laboratory investigations that monitor the stress and strain variations during hardening need to be performed to further support this assumption and quantify the evolution of s.

(4) Poro-elastic bulk shrinkage is assumed to occur in the plane perpendicular to the wellbore axis; no axial shrinkage is assigned. By the time the cement becomes immobile, the cement is constrained by the friction between the casing and formation and thus the axial deformation is restricted(Nelson and Guillot, 2006).

(5) In order to simplify the simulation of the coupled chemothermo-poro-elastic processes during cement shrinkage,this study simulates the shrinkage process as a timedependent bulk volume variation and continuously updates the cement poro-elastic properties (Section 2.2.2), and the pore pressure(Section 2.2.2).

Fig. 4. Input elastic bulk shrinkage for the SDCS-BaseCase (adapted from Chenevert and Shrestha, 1991) and the input degree of hydration varying with time (adapted from Pang et al., 2013).

2.2.2. Cement poro-elastic properties obtained for downhole conditions

Laboratory and numerical studies of Ghabezloo et al.(2008)and Agofack et al. (2019) have pointed out that the poro-mechanical behavior is an essential cement property that cannot be ignored when characterizing the cement response to external loads. Bois et al. (2011, 2012) further proposed that the poro-mechanical behavior also needs to be considered in modeling the cement hardening process, especially for simulating the pore pressure variation. This study adopts the relationships between each poroelastic parameter and the degree of hydration, ξ (Fig. 4) from Samudio (2017), including drained bulk modulus (Kd) and Biot’s coefficient(α).The grain bulk modulus is calculated by Eq.(1)and the fluid bulk modulus is 22 GPa (Fig. 5):

The Young’s modulus (E) and Poisson’s ratio (ν) are calculated from the acoustic measurements during cement curing at 60°C,as shown in Fig. 5 (Bourissai et al., 2013). The temporal relationship between the curing time and degree of hydration is also adapted from Bourissai et al. (2013) (Fig. 5).

2.3. Cement pore pressure development

Fig. 5. The input parameters of grain bulk modulus (Kg), Young’s modulus (E), and Poisson’s ratio (ν) with respect to the degree of hydration (ξ) for SDCS-BaseCase. The grain bulk modulus is calculated from the poro-elastic parameters from Samudio(2017). The Young’s modulus and Poisson’s ratio data are adapted from Bourissai et al. (2013) and converted from dynamic values to static values based on the approach of Lee et al. (2017).

The cement pore pressure reduction is a critical component of the hardening process. Due to the ultra-low permeability developed in the cement after hardening(Nelson and Guillot,2006),the pore space in the cement matrix becomes hydraulically isolated from the formation.A pore pressure lower than the formation pore pressure may develop in the cement during the‘Cement hardening’step, which may equilibrate to the formation pore pressure over long-term production/injection scenarios (Appleby and Wilson,1996; Bois et al., 2011, 2012). The magnitude of the pore pressure reduction is directly affected by the formation water supply,curing temperature, and curing pressure (Nelson and Guillot, 2006; Bois et al., 2011). The pore pressure input for the base case is adapted from Cooke et al.(1983),Reddy et al.(2009)and Zhang et al.(2017),which is measured under 10 MPa confining pressure with abundant external water supply. The cement pore pressure is initially assigned to drop 20%linearly during the simulation time of loading step 4 (SDCS-BaseCase in Fig. 3). Sensitivity analyses ranging from 0%(Appleby and Wilson,1996)to 100%pore pressure drop(Levine et al.,1979; Reddy et al., 2009) are performed (Table 2).

2.4. Simulation of cement shear failure

Shear failure is likely to occur in the cement when excessive pressure is applied to the casing. In this study, the occurrence of shear failure of both the cement and the formation is governed by a Drucker-Prager failure criterion (Menetrey and Willam,1995). The damage plasticity model developed by Lubliner et al. (1989) and Lee and Fenves (1998) is used to analyze the data from triaxial compression test of class G cement to obtain post-failure parameters for the numerical model (Arjomand et al., 2018). The relation between the test data and post-failure parameters is shown below(SIMULIA, 2017):

where σcis the axial compressive stress(Pa);is the elastic strain measured at the end of the elastic period;E0is the Young’s modulus measured at the end of the elastic period (Pa);andare the equivalent plastic and inelastic strains, respectively; and dcis the damage index describing the severity of damage. The triaxial test data of Class G cement cured at 1000 psi (1 psi = 6.89 kPa) from Philippacopoulos and Berndt(2001)are used to calculate the input parameters (i.e.for the Drucker-Prager failure criterion. All parameters for the formation rock are collected from Busetti et al.(2012).

2.5. Interface bond modeling

The failure of the interface bonds and the development of an MA are simulated using cohesive interface elements via a traction separation law. This approach has been well documented in the literature (Wang and Taleghani, 2014; Feng et al., 2016; Arjomand et al., 2018) and is therefore only shortly summarized in Appendix A.

3. Modeling approach validation

In order to ensure the validity of the results with respect to the staged FEA approach and the failure characterization used, the modeling procedure described in Section 2.1.2 is used to reproduce the well documented first experiment of Jackson and Murphey (1993). Once the numerical modeling approach is benchmarked, the results of the sensitivity analyses (Table 2) are used to discuss differences and importance of simulating downhole conditions.

Fig. 6. (a) The effective radial and hoop stresses at the inner cement and the contact pressure at the inner casing-cement interface during pressure testing for the numerical reproduction of Jackson and Murphey(1993)’s experiment.(b)The tolerance pressures(Ptolerance) obtained from the numerical reproduction (blue dot) of the experiment of Jackson and Murphey (1993). The blue region represents the range of the tolerance pressure for which shear failure occurs in Jackson and Murphey (1993). Dashed black lines are the Ptolerance range observed by Goodwin and Crook(1992)and the red cross is a possible minimum value of Ptolerance observed by Therond et al. (2017).

3.1. The experiment

The laboratory experiment apparatus includes a 5 in.(127 mm)inner casing,a 7 in.(177.8 mm)outer casing,and Class G cement in the annulus. The cement is cured under 120°F (48.889°C) and 1000 psi for 69 h. Then, the pressure is released and a 100 psi air pressure difference is applied between the top and bottom of the annulus. The following pressure cycles are applied to the inner casing: (1) Start with an initial inner casing pressure of 1000 psi,increase the inner casing pressure to 2000 psi, and keep the apparatus undisturbed for 10 min; (2) Reduce the pressure to 1000 psi and keep the apparatus undisturbed for 10 min; (3)Repeat cycles (1) and (2) with a 2000 psi increment until the maximum testing pressure of 10,000 psi. The maximum inner casing pressure that the system can withstand without cement failure(as indicated by resulting gas flow through the annulus)is recorded as Ptolerance. Jackson and Murphey (1993) observed that no gas flow is detected at the maximum inner casing pressure until the end of the 6000 psi cycle. Following the 8000 psi pressure cycle, gas flow occurs when the inner casing pressure is reduced down from 8000 psi to 1000 psi.

3.2. Numerical reproduction

A staged FEA approach is utilized to reproduce the laboratory setup/experiment. The exact dimensions and geometric components(inner casing,cement,and outer casing)are discretized into a finite element mesh. The top and bottom of the model are constrained axially reflecting the experimental setup. Due to the similar curing conditions, the temporal variations of the material property parameters of the cement are the same as those for the SDCS-BaseCase (Table 1 and Fig. 5). After the cement is set, the cyclic pressure boundary conditions applied to the inner casing are identical to the test of Jackson and Murphey (1993).

3.3. Results and benchmarking

In the numerical modeling adaptation,the state of stress at the cement elements adjacent to the inner casing (i.e. termed ‘inner cement’) is recorded and presented from the beginning of the pressure cycle to the occurrence of cement failure;pressure cycles with lower pressure for which no failure occurs are not presented.Instead of observing an increase in annular air flow,the occurrence/onset of plastic strain (i.e. the numerical approach applies a Drucker-Prager failure criterion with the strength properties as shown in Table 1)is used to determine the maximum inner casing pressure that the system can withstand(Ptolerance).Fig.6a shows the radial and hoop stresses at the inner cement and the contact pressure between the inner casing and the cement with respect to changes of the testing pressure imposed on the inner casing after cement hardening. The modeling results show that shear failure occurs when the inner casing pressure reaches 49.5 MPa(Ptolerance).Ptoleranceof the numerical solution (Fig. 6b) is in close agreement with the data ranges observed by Goodwin and Crook (1992),Jackson and Murphey (1993), and Therond et al. (2017). Since the simulation result is in agreement with the laboratory observations,the initial estimate of s (0.5) is preliminarily applied in the staged downhole condition scenarios (Table 2). A sensitivity analysis of this parameter is performed in Section 5.3.

4. Results

4.1. Staged downhole condition scenarios (SDCS) during cement hardening

Fig.7. Effective radial stresses at the inner(purple dashed line)and outer sides(green dashed line) of the cement component, and contact pressure at the casing-cement(blue line) and cement-formation (red line) interfaces during the hardening stage.

The results for the staged downhole condition scenarios(SDCS)will quantify both the temporal and spatial evolution and distribution of the following parameters during the cement hardening process: radial stress, contact pressure at the casing-cement and the cement-formation interfaces, and the resulting debonding aperture.The results of various sensitivity analyses with respect to cement pore pressure variation, cement shrinkage, and temperature fluctuation are presented and correlated with respect to a base case scenario (SDCS-BaseCase). It is important to note that the results in this section comprise loading steps 1-4 only;shear failure does not occur for any scenario during hardening (except for the scenarios of cement under extreme shrinkage, which will be subsequently excluded).

4.1.1. The base case

The SDCS-BaseCase is the reference case of this study and is used as the benchmark for analyzing the influence of various factors during cement hardening. Fig. 7 shows the temporal evolution of effective radial stresses and contact pressure at the inner and outer interfaces of the cement component.The inner cement radial stress has an initial magnitude of 6.2 MPa (the cement slurry pressure minus pore pressure)10 h after the cement slurry is placed,and it increases to 6.7 MPa at the end of the ‘Cement hardening’ step(after 50 h).The radial stress at the cement elements adjacent to the formation (i.e. termed ‘outer cement’) decreases from 6.2 MPa to 3.9 MPa at the end of the ‘Cement hardening’ step. During the‘Cement hardening’step,the contact pressure between casing and cement drops from 14 MPa to 12.1 MPa. The contact pressure between cement and formation drops from 4.2 MPa to 0.8 MPa ultimately. Since the contact pressures of both interfaces do not become tensile (< 0 MPa), no MA is initiated.

Fig.8. The contact pressure variation during the cement hardening for various degrees of cement pore pressure drop at (a) Casing-cement interface, and (b) Cementformation interface(minimum values for each scenario are labeled with red triangles).

4.1.2. Cement pore pressure drop during hardening

Fig. 8 shows the contact pressure at the interfaces of the sensitivity analysis of the applied linear pore pressure drops of 0%,20%, 50%, 75%, and 100% during the hardening process for SDCSPpDrop.At the casing-cement interface(Fig.8a),for 20%,50%,75%,and 100% pore pressure reductions during hardening, the contact pressure decreases from 14 MPa to 12.1 MPa,11.7 MPa,11.4 MPa,and 11.1 MPa, respectively. For 0% pore pressure reduction, a decrease from 14 MPa to 12.56 MPa(after 36.5 h)occurs,followed by an increase to 12.74 MPa. At the cement-formation interface(Fig. 8b), for 20%, 50%, 75%, and 100% pore pressure reductions during hardening, the contact pressure decreases from 4.2 MPa to minimum values of 0.78 MPa, 2.42 MPa, 3.35 MPa, and 3.96 MPa after 45 h, 31 h, 25 h, and 20 h, respectively, and then recovers to 0.8 MPa, 3.1 MPa, 5 MPa, and 6.9 MPa, respectively. For 0% pore pressure reduction, the contact pressure reduces to -0.36 MPa until the end of the ‘Cement hardening’ step. For this case, an MA initiates after 36.5 h when the contact pressure at the cementformation interface reaches zero.

Fig. 9. (a) The contact pressure at the casing-cement interface for different s values applied; (b) The contact pressure at the cement-formation interface; and (c) The MA aperture for scenarios that initiate MA.

4.1.3. Cement shrinkage with different poro-elastic bulk shrinkage coefficients

For SDCS-Shrinkage, the influence of different s values on the state of stress evolution during cement hardening is shown in Fig.9.

At the casing-cement interface, for the scenario s = 0, the contact pressure slightly increases from 14 MPa to 14.1 MPa at the beginning and gradually decreases to 13.95 MPa. For the scenario s=0.25,the contact pressure decreases from 14 MPa to 13 MPa.For the scenarios s = 0.75 and 1, the contact pressure decreases from 14 MPa to minimum value of 12 MPa after 21 h and 26 h, and suddenly increases back to 14.1 MPa and 12.1 MPa,respectively,by the end of the step. This increase can be explained by the debonding at the cement formation interface. As shrinkage continues, due to the debonding between cement and formation, the casing and cement components become isolated from the formation, and the cement shrinkage becomes a pure centripetal deformation, thus increasing the compression at the casing-cement interface.

At the cement-formation interface, during the cement hardening, the contact pressure for s = 0 increases from 4.2 MPa to 6.26 MPa. For s = 0.25, the contact pressure drops slowly from 4.2 MPa to 3.55 MPa.For s=0.75 and 1,the contact pressure drops from 4.2 MPa to 0 MPa after 26 h and 21 h, to -0.5 MPa (tensile bond strength) after 31 h and 23 h, respectively, and keeps this value until the end. For s = 0.75 and 1, the MA initiates at the cement-formation interface when the contact pressure reaches 0 MPa (after 26 h and 21 h) and respectively reach ～17 μm and～49 μm by the end.

4.2. Staged downhole condition scenarios (SDCS) after cement hardening

Based on the state of stress developed during the ‘Cement hardening’ step, subsequent loading steps (5 and 6) representing pressure testing and injection-related cooling are simulated to investigate the conditions for MA occurrence and severity. For loading steps 5 and 6, shear failure is also investigated. Sensitivity analyses and the combined effect associated with the factors during cement hardening are investigated in Section 5.

4.2.1. Pressure testing

For SDCS-BaseCase-PTesting (Fig. 10a and b), the pressure applied on the inner casing (testing pressure) increases from the mud pressure (12 MPa) to a maximum pressure of 40 MPa (a representative value during pressure testing in Postler (1997)).While the contact pressures remain compressive throughout pressure testing (i.e. no debonding failure occurs), the equivalent plastic strain (PEEQ) in the cement is monitored as an indicator of shear failure (Fig.10a). The PEEQ at the outer cement elements is zero and not shown in Fig.10b.PEEQ at the inner cement develops at a testing pressure of 30 MPa,which indicates Ptolerance=30 MPa,and PEEQ reaches a magnitude of 1.03 × 10-4for an inner casing pressure of 40 MPa.For SDCS-TempFluc-PTesting,which considers the temperature fluctuation during hardening, PEEQ at the inner cement initiates at a testing pressure of 23.4 MPa and PEEQ reaches a magnitude of 2.26×10-4for an inner casing pressure of 40 MPa.For SDCS-PpDrop-PTesting, only two end-member scenarios (i.e.cement pore pressure drop of 0% and 100% during hardening) are presented (due to the minor differences; light blue and purple dashed lines in Fig.10b). For pore pressure drops of 0%, 50%, 75%,and 100%,the Ptolerancevalues are 28.1 MPa,32.5 MPa,34.8 MPa,and 37.2 MPa,respectively.For SDCS-Shrinkage-PTesting,with s=0 and 0.25, the Ptolerancevalues are 68 MPa and 47.5 MPa, respectively(Fig.10c).

Fig. 10. (a) Illustration of the equivalent plastic strain (PEEQ) distribution when the inner casing pressure is 40 MPa.(b)The resulting PEEQ changes with the applied inner casing pressure during the pressure testing for SDCS-BaseCase-PTesting(blue line)and SDCS-BaseCase-TempFluc(green line).(c)The resulting PEEQ variation during pressure testing for SDCS-PpDrop-PTesting and SDCS-Shrinkage-PTesting.

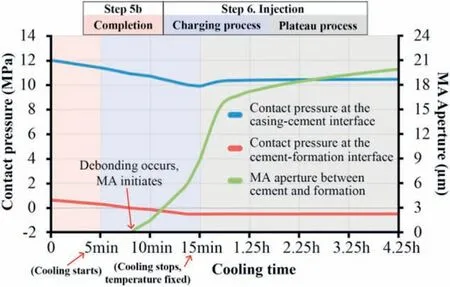
Fig.11. Contact pressure at the casing-cement and cement-formation interfaces, and the resulting MA at the cement-formation interface during the ‘Completion’ and ‘Injection’ steps (see Section 2.1.2).

4.2.2. Injection-related cooling

For SDCS-BaseCase-Cooling(Fig.11),the contact pressure at the casing-cement interface decreases from 12 MPa to 11.4 MPa during the ‘Completion’ step (red area), and to 9.9 MPa by the end of the‘Charging process’ (blue area), which stabilizes at 10.3 MPa (grey area). The contact pressure at the cement-formation interface drops from 0.8 MPa to 0.3 MPa during the ‘Completion’ step, and then to zero after 3 min of the ‘Charging process’, which reaches -0.5 MPa by the end of the ‘Charging process’, and stabilizes at -0.5 MPa. The resulting MA reaches the aperture of～20 μm by the end of the ‘Plateau process’. The influences of cement pore pressure decrease, shrinkage, and temperature fluctuations are presented in Section 5.

5. Discussion

The results in this study show significant differences with the majority of previous staged finite element modeling studies in terms of MA occurrence and cement failure conditions and locations.In contrast to studies by Ravi et al.(2002),Gray et al.(2009),Nygaard et al.(2014),and Li and Nygaard(2017),this study includes a cement hardening step that considers the combination and integration of the major mechanical processes under downhole condition, including: (1) the development of cement poro-elastic properties, (2) pore pressure variations, and (3) volumetric bulk shrinkage. The modeling approach for cement hardening in this study is qualitatively compared to the analytical modeling approach by Bois et al. (2011, 2012), which includes theoretical cement hydration modeling for a chemo-poro-mechanical cement system.The following sections discuss the importance of downhole conditions (for the base case followed by loading steps 5 and 6 in Section 5.1), and the occurrence and evolution of MA due to the individual and combined influences of cement hardening,pressure testing, and injection-related cooling are investigated and sensitivities of factors from the three processes are discussed with respect to their importance and implications (Sections 5.2-5.4).

5.1. Importance of downhole conditions

A representative simulation of loads occurring during the wellbore life span,especially during cement hardening,is critical to achieving downhole conditions, and thus enables quantitative evaluation of MA initiation and evolution (Bois et al., 2011; De Andrade et al., 2015). In this study, the validation process (Section 3)shows that the approach used(including the cement hardening process)is capable of reproducing the laboratory test of Jackson and Murphey(1993)and of predicting the occurrence of cement failure that matches the laboratory observations. The close agreement between the results in Section 3 is a strong indicator that the modeling approach can be successfully transferred and adapted to simulate downhole conditions accounting for the life cycle of a production/injection well.

5.1.1. During cement hardening

For the base case scenario (SDCS-BaseCase), the cement hardening process is modeled considering poro-elastic property development, bulk shrinkage, and the pore pressure decrease.Based on the assumption of an initial compressive state of stress in the cement before cement hardening, the contact pressure at the beginning of the‘Cement hardening’step is 4.2 MPa at the cementformation interface (slurry pressure minus pore pressure) and 14 MPa at the casing-cement interface (slurry pressure). The assumption of an initial effective compressive stress state represents a reasonable condition based on laboratory experiments(Boukhelifa et al., 2005; De Andrade et al., 2015) and numerical studies(Gray et al.,2009;Li and Nygaard,2017;Zhang et al.,2017;Lavrov,2018).A tensile or zero effective stress state after hardening implies immediate failure for any scenario (Bois et al., 2011;Nygaard et al., 2014).

During cement hardening, the poro-elastic bulk shrinkage decreases the degree of compression at the cement interfaces,and the radial stress at the outer side of the cement sheath decreases by 2.36 MPa, while it increases by 0.45 MPa at the inner side (SDCSBaseCase in Fig.7).The variation of cement radial stress reduces the contact pressures at both interfaces,and for the cement-formation interface (with a contact pressure of 0.8 MPa in Fig. 7), tensile debonding is likely to occur.The result of this study is in agreement with observations obtained from computed tomography(CT)scans by De Andrade et al. (2015), who showed that debonding mainly occurs at the cement-formation interface after cement hardening.By the end of the hardening process, the resulting radial stress distribution across the cement sheath (Fig. 7) and the different contact pressures at the casing-cement and the cement-formation interfaces indicate that the cement no longer has a uniform and isotropic state of stress, which is a common assumption in many staged finite element studies(Gray et al.,2009;Nygaard et al.,2014;Li and Nygaard, 2017). This difference can lead to different predictions of MA generation.

5.1.2. During pressure testing

In order to evaluate the response of the cement sheath with respect to its sensitivity to increases of the inner wellbore pressure,the modeling results (SDCS-BaseCase-PTesting) show that shear failure occurs at the casing-cement interface (inner side of the cement sheath) for an applied inner casing pressure of 30 MPa(Fig.12). While the occurrence and location of shear failure due to pressure loading are qualitatively in agreement with the laboratory results of Goodwin and Crook (1992) and Jackson and Murphey(1993), as shown in Fig. 6b, significant differences exist. The tolerance pressure of the SDCS-BaseCase-PTesting scenario (30 MPa) is much lower than those of 42-55 MPa(Fig.7)reported by Goodwin and Crook (1992) and Jackson and Murphey (1993). These values are representative of equivalent depths of 500-700 m (based on their cement curing pressures and temperatures applied). It is noted that the exact numerical adaptation of their laboratory setup reproduces their results (Fig. 6b). However, in order to obtain a more representative evaluation of shear failure, downhole conditions should be considered.The tolerance pressures obtained from SDCS-BaseCase-PTesting are: 24.3 MPa for 500 m, 30 MPa for 1000 m, 38.1 MPa for 1500 m, and 41.6 MPa for 2000 m depth(Fig.12 and Table C1 in Appendix C).The increase of Ptolerancewith respect to depth is in agreement with literature studies showing that the wellbore system maintains better integrity for larger depths (De Andrade and Sangesland, 2016; Lavrov, 2018).Compared to Goodwin and Crook (1992), the lower magnitudes obtained numerically are in the range of observations obtained from leak-off tests,as shown in Fig.12(Postler,1997;King and King,2013).It needs to be noted that a direct evaluation and comparison should be considered carefully (and may not be appropriate) as wellbore pressures obtained from leak-off tests are representative of the integrity of the casing shoe (i.e. for a different and weaker location of the wellbore than that considered in this study)(Postler,1997;Nelson and Guillot,2006;API,2009).The results of this study can be used as a reference to narrow down the prediction of shear failure occurrence and optimize the operation parameters for wellbore operations, such as testing pressures.

Fig.12. Comparison of prediction of the inner casing pressure to initiate shear failure(Ptolerance) in SDCS-BaseCase-PTesting for different depths (red dots), hydrostatic pore pressures for different depths,and leak-off pressures indicative of casing shoe integrity(Postler,1997).

5.1.3. During completion/production

During the ‘Completion’ step (the first part of SDCS-BaseCase-Cooling in Fig. 11 with pink block), when the inner casing pressure drops and before cooling is initiated, the modeling results show that the contact pressure at both cement interfaces decreases,and for the cement-formation interface, the likelihood of debonding failure increases. This result is in agreement with the ‘reduced hydrostatic scenario’ of Jackson and Murphey (1993), and the numerical prediction of Orlic et al. (2018). For some staged finite element studies that ignore the cement hardening process and associated state of stress variation (Ravi et al., 2002; Gray et al.,2009), an MA is predicted to initiate at the casing-cement interface due to wellbore pressure decrease (inner casing pressure).However, a moderate inner casing pressure drop (i.e. 18% in this study) is not sufficient to overcome the significant compression at the casing-cement interface and induce debonding failure. Even a large inner pressure reduction (i.e. 40% drop, as adapted from the production stage in Gray et al. (2009) and De Andrade and Sangesland (2016)) (red line in Fig. 13) is not enough to initiate an MA.MA initiation requires a drawdown of 46%,and an extreme drawdown (e.g. 60%) can result in a small MA aperture of ～2 μm(red dashed line in Fig. 13). It is noted that the analysis of MA initiation of this study is based on the poro-elastic behavior of cement and formation. Creep behavior of cement and formation over a large time scale (i.e. years) can inhibit the development of MA(Lavrov and Torsæter,2016;Lavrov,2018).Hence,the long-term pressure drawdown effects due to production may not have significant impacts on MA generation and development.

Fig. 13. Variation of the contact pressure at the cement-formation interface with different degrees of drawdown of the inner casing pressure. Contact pressures are in solid lines and the resulting MA apertures are shown in dashed lines.

5.2. During injection-related cooling

For the injection-related cooling during the ‘Injection’ step(SDCS-BaseCase-Cooling), an MA initiates during the ‘Charging process’ at the cement-formation interface (blue block in Fig.11).The contact pressure between the cement and formation(0.4 MPa,by the end of the ‘Completion’ step) is further decreased by the tensile stress induced by cooling.An MA starts to develop when the contact pressure drops below zero and the interface becomes fully debonded when the contact pressure reaches the tensile bond strength of -0.5 MPa (Fig. 11). MA generation at the cementformation interface during injection-related cooling is in agreement with the modeling result of Orlic et al. (2018). Fig. 11 also shows that during the ‘Charging process’, the contact pressure at the casing-cement interface decreases by 1.5 MPa, while the contact pressure at the cement-formation interface decreases by 0.9 MPa. The tendency that the contact pressure at the casingcement interface is affected more significantly by the cooling than the cement-formation interface is in agreement with the qualitative analysis of Bois et al. (2011). Due to the state of stress previously developed in the system,the casing-cement interface is under significant compression and inhibits MA generation; the cement-formation interface has less compression and promotes MA occurrence (Orlic et al., 2018). These observations are in contrast to numerical studies assuming an isotropic state of stress or a zero effective stress in the cement, which results in MA initiation at the casing-cement interface (Ravi et al., 2002; Bois et al.,2011).

During the ‘Plateau process’ (gray block in Fig. 11), MA development slows down due to the fixed temperature at the inner casing. The final MA aperture is ～20 μm after 4 h of the ‘Plateau process’. This aperture falls into the range of hydraulic MA apertures provided in the thermal debonding scenario of Stormont et al.(2018) and of the numerical prediction of Orlic et al. (2018).

5.3. Influence of cement pore pressure evolution during hardening

As detailed knowledge about the initial pore pressure magnitude in the cement during hardening is sparse and only monitored over a short period of time,i.e.48 h(Reddy et al.,2009),this study considers cement pore pressure drops of 0%, 20% (BaseCase), 50%,75%, and 100% (SDCS-PpDrop). Fig. 8 shows that different pore pressure drop scenarios result in different contact pressures at both cement interfaces at the end of the‘Cement hardening’step.For the cement-formation interface (which has the lower overall contact pressures), a higher pore pressure drop results in a higher contact pressure by the end of the‘Cement hardening’ step (Fig. 8b).After the ‘Hardening stage’, pressure testing results (SDCS-PpDrop-PTesting in Fig. 10b) indicate that the pore pressure drop in the cement from 0% to 100% increases Ptolerencefrom 28.1 MPa to 37.2 MPa and a shear failure induced MA can be generated. This slight increase is due to the pore pressure-stress coupling of the cement component as a poro-elastic material (Ghabezloo et al.,2008; Bois et al., 2011).

The contact pressure further decreases when the injectionrelated cooling starts; for scenarios of cement pore pressure drops of 20% and 50%, debonding failure occurs and MA initiates(Fig.14a) at the cement-formation interface. For 0% pore pressure drop,debonding failure has already occurred during the hardening process; as a result, the contact pressure remains constant. After the injection-related cooling process,the MA apertures for 0%,20%,and 50% cement pore pressure drops are ～32 μm, ～20 μm, and～2 μm, respectively(Fig.14b).

Fig.14. Injection-related cooling results during the ‘Completion’ and ‘Injection’ steps(see Section 2.1.2) for cement systems with different degrees of pore pressure drop during hardening:(a)Contact pressure at the cement-formation interface;and(b)The resulting MA aperture for scenarios with debonding occurring during injection-related cooling.

The results show that, during injection-related cooling,debonding failure (MA) is more likely to occur when the cement pore pressure drops are less during hardening. This is because a lower pore pressure drop results in a lower compressive state of stress in the cement,and thus the wellbore system is less resilient against the tensile stress induced by cooling. This result is in agreement with the mathematical modeling of cement pore pressure variation of Bois et al.(2011)and with De Andrade et al.(2015),who showed that the wellbore system is less likely to initiate debonding failure during cooling if the cement is cured under larger compressive stress.

It is important to note that quantitative measurements of the evolution of cement pore pressure magnitudes under downhole conditions are currently not available in the public domain, and future research in this direction is recommended to evaluate the significance of the pore pressure evolution on cement sheath integrity (and therefore as a required input parameter for numerical models).

5.4. Influence of poro-elastic bulk shrinkage coefficient

During cement hardening,the shrinkage is the combined result of multiple factors which are involved in the complicated chemothermo-poro-mechanical process. Some of these factors are incorporated in the modeling approach of this study(i.e.thermal,poroelasticity,and pore pressure variation),while the others are ignored due to inadequate laboratory investigations and difficulty in quantification(Bourissai et al.,2013;Samudio,2017).In this study,the mechanical influence of the cement volumetric shrinkage is quantified and simplified by introducing the poro-elastic bulk shrinkage coefficient(s).Fig.9 shows that different bulk shrinkage coefficient scenarios (SDCS-Shrinkage) result in different contact pressures at both cement interfaces at the end of the ‘Cement hardening’step.For the cement-formation interface(which has the lower overall contact pressures), a higher coefficient results in a lower contact pressure by the end of the ‘Cement hardening’ step(Fig. 9b). The pressure testing results (SDCS-Shrinkage-PTesting in Fig. 10c) show that for s = 0.75 and 1, shear failure has already occurred before the start of pressure testing.For s=0.5(base case),0.25,and 0,the Ptolerancevalues are 30 MPa,47.5 MPa,and 68 MPa,respectively. The significant increase of Ptolerancewhen s decreases can be explained by the reduction of differential stress when the cement shrinks less.

For SDCS-Shrinkage-Cooling, the contact pressure further decreases when the injection-related cooling starts;for s=0 and 0.25,debonding does not occur;for s=0.5,debonding failure occurs and MA initiates (Fig.15a). For s = 0.75 and 1, debonding has already occurred during hardening and the contact pressure remains constant.After the injection-related cooling process,the MA apertures for s = 0.5, 0.75 and 1 are ～20 μm, ～50 μm, and ～81 μm,respectively(Fig.15b).

Fig.15. Injection-related cooling results for cement systems with different degrees of pore pressure drop during hardening: (a) Contact pressure at the cement-formation interface, and (b) The resulting MA aperture for scenarios with debonding occurring during injection-related cooling.

In order to determine an appropriate range for s during downhole conditions, the numerical modeling results are evaluated based on observations obtained throughout several laboratory experiments. The cement bulk shrinkage data in this study are based on the measurement of Chenevert and Shrestha (1991)under 100°F and 1200 psi(which is equivalent for ～800 m depth and close to the 1000 m depth considered in SDCS-BaseCase).For a cement cured at 150°F and 500 psi, which has a lower initial compressive stress than the cement of Chenevert and Shrestha(1991), De Andrade et al. (2015) did not observe systematic debonding failure for the casing-cement-formation system after hardening based on high-resolution CT scans. No significant further debonding is observed after several cooling cycles with a temperature difference of 284°F (140°C). Based on this observation,a reasonable conclusion is that the cement system is under a substantial compressive stress. Therefore, the s values of 0.75 and 1 are considered inappropriate due to debonding and shear failure occurring during cement hardening. The remaining range of coefficients is considered reasonable, covering shrinking neat class G cement (s = 0.5) and cements treated with additives that prevent the degree of shrinking (s = 0.25 and 0). This result is in agreement with the laboratory observation of Boukhelifa et al.(2005), who showed that for a cement system which shrinks less during hardening, tensile stresses and hence failure are less likely to develop/occur, and with the common practice in the oil industry to prevent the cement from shrinking (Nelson and Guillot, 2006; Kurdowski, 2014). This study is the first to quantify this effect under downhole conditions, which enables to quantify the resulting MA aperture with respect to the degree of shrinkage.

5.5. Influence of cement temperature fluctuation during hardening

Temperature fluctuations during hydration reaction and associated thermal stress are also considered as contributors to the cement state of stress (Bois et al., 2012). Air circulation for heat emission and enough curing time are standard procedures during concrete curing (Kurdowski, 2014). Since direct temperature measurements for downhole conditions,to the authors’knowledge,are not publicly available, the input temperature data for SDCSTempFluc are qualitatively adapted from the rate of hydration(heat emission) measured by Pang et al. (2013) and from temperature measurements during concrete hardening(Zhou et al.,2014),as shown in Fig. 16 (a detailed description of this qualitative adaptation is presented in Appendix D). The most significant heat generation (black line) and temperature increase (blue and green lines)occur during Stages I and III of hydration,during which they have a less significant contribution to the final state of stress due to the fluid behavior of the cement. During Stage IV, the cement temperature starts to decrease (due to the decrease of heat production), while the cement behaves more and more elastic and Young’s modulus increases significantly(Nelson and Guillot,2006;Kurdowski,2014).Hence,this cooling of the cement induces tensile thermal stresses,which can decrease the contact pressure between casing-cement and cement-formation and further promote MA occurrence (Bois et al., 2012). This tensile stress also increases the differential stress, and hence promotes the occurrence of shear failure during pressure testing(green line in Fig.10b).In this study,this temperature fluctuation during cement hardening is simulated(SDCS-TempFluc in Table 2) in two stages. The first stage is a pure heat conduction process using the temperature increase in the cement(blue line in Fig.16)as an input to predict the temperature variation in the entire model domain. Then, the resulting temperature field is applied as the initial condition for the second stage,during which the cement temperature variation (green line in Fig.16)is coupled with other physical processes(i.e.poro-elasticity,pore pressure,and shrinkage variations).

Fig.16. Temperature input for the cement of the temperature fluctuation scenario. The blue section represents the temperature input for the thermal analysis before the cement hardening simulation. The temperature field calculated from this thermal analysis step is used as the initial condition for the SDCS-TempFluc. The green part is the input temperature of SDCS-TempFluc. Cement temperature are qualitatively adapted from Pang et al. (2013) and Zhou et al. (2014).

Fig. 17. (a) Contact pressure at the casing-cement and cement-formation interfaces and in the center of the cement sheath during hardening.(b)Comparison of injectionrelated cooling results (contact pressures and MA apertures) for hydration-related temperature fluctuation for SDCS-TempFluc-Cooling and the base case SDCS-Base-Case-Cooling.

The modeling result of SDCS-TempFluc with respect to debonding during the ‘Cement hardening’ step is presented in Fig. 17a. When the temperature in the cement sheath decreases from 55°C to 47.5°C, the contact pressure at the casing-cement interface drops by 2.5 MPa; and at the cement-formation interface, it decreases by 3.77 MPa. For SDCS-BaseCase, it decreases by 1.9 MPa and 3.42 MPa at the casing-cement and cement-formation interfaces, respectively. For SDCS-TempFluc-PTesting (Fig. 10b),shear failure initiates for an inner casing pressure of 23.4 MPa,which is 6.6 MPa lower than that without considering temperature fluctuation (SDCS-BaseCase-PTesting). During injection-related cooling, the contact pressure at the cement-formation interface reaches zero earlier,i.e.from 0.43 MPa to 0 during the‘Completion’step (red line in Fig.17b) and MA initiates (compared to MA initiation during the ‘Charging process’ for SDCS-BaseCase-Cooling;blue line in Fig.17b). The final MA aperture is ～23 μm for SDCSTempFluc-Cooling and ～20 μm for SDCS-BaseCase-Cooling. It is observed that temperature fluctuation during cement hardening promotes MA initiation and evolution in a moderate degree is in agreement with the qualitative analysis of Bois et al. (2011), who showed that temperature fluctuation is only important when the contact interface is close to debonding.

Fig. 18. (a) The maximum inner casing pressure the wellbore system can withstand without shear failure (Ptolerance) for staged downhole conditions scenarios. (b) The temperature decrease required to initiate MA during injection-related cooling for staged downhole conditions scenarios.

5.6. Summary of factors affecting MA occurrence

In order to evaluate the factors contributing to MA occurrence, various downhole scenarios presented in Table 2 are compared and evaluated with respect to the required maximum inner casing pressure, Ptolerance, necessary to initiate shear failure at the inner cement sheath (Fig. 18a), and the required temperature drop necessary to initiate debonding at the cementformation interface during injection-related cooling (Fig.18b).

With respect to Ptolerance, Fig.18a shows that:

(1) The poro-elastic bulk shrinkage coefficient is a significant parameter. Smaller magnitudes of s (i.e. a smaller degree of poro-elastic volumetric shrinkage) result in a lower magnitude of differential stress and thus a higher Ptolerancecan be sustained;hence,the less the cement shrinks,the better the cement integrity is.

(2) The cement pore pressure decrease during hardening has a minor influence on Ptolerance.From 0%to 100%of the cement pore pressure decrease, Ptoleranceonly increases from 28.1 MPa to 37.2 MPa.

(3) Temperature fluctuations during the hardening process decreases Ptolerancefrom 30 MPa (SDCS-BaseCase-PTesting) to 23.4 MPa, as the cooling effect during the later stage of the‘Cement hardening’step increases the differential stress.This observation is significant as the cement is weakened.

(4) Cement integrity increases with increasing depth.

With respect to the required temperature drop to initiate debonding,Fig.18b shows that:

(1) The poro-elastic bulk shrinkage coefficient also affects the tolerance of the system against debonding due to injectionrelated cooling. For s = 0, 0.25, and 0.5, debonding occurs at the cement-formation interface after temperature decreases of 112°C, 68°C, and 10°C, respectively. Higher temperature differences during cooling can be sustained for low cement bulk shrinkage; hence, the lower the cement shrinks, the better the cement integrity is.

(2) The cement pore pressure decrease has a significant influence on the tolerance of the system against injection-related cooling induced MA.For pore pressure decrease of 20%,50%,75%, and 100%, debonding occurs at the cement-formation interface after the temperature decreases of 10°C, 44°C,75°C, and 103°C, respectively. That is to say, if the cement pore pressure decreases more, higher temperature differences can be sustained. Since quantitative measurements of cement pore pressure evolution for downhole conditions are not publicly available,further researches in this direction are recommended.

(3) Temperature fluctuations promote initiation of debonding failure.This is due to the cooling effect occurring during the‘Cement hardening’ step which induces tensile thermal stresses and decreases the contact pressure at the cementformation interface. Ignoring cement temperature fluctuation may lead to underestimation of MA occurrence and resulting MA aperture. This factor is important when the contact pressure at the interface is close to debonding,but it is not enough to initiate MA at the interface under large compression by itself.

(4) Cement integrity increases with increasing depth.

5.7. Implications for design of field operations

Based on the modeling results, several suggestions can be provided for field operations to reduce the likelihood of MA occurrence:

(1) Accelerators can speed up the cement hydration reaction,promote the development of the ultra-low permeability cement matrix, impede formation water from entering the cement, and enhance the cement pore pressure decrease.Adding a moderate amount of accelerators to the cement slurry thus helps to mitigate the debonding and shear failure risks.

(2) Expanding additives are an essential component in controlling the bulk shrinkage of the cement system and reducing the risk of debonding and shear failure.However,the amount of expanding additives should be carefully evaluated(e.g.by using the proposed approach of this study)to avoid inducing excessive compressive stress and increasing shear failure risk.

(3) For pressure testing performed after cement hardening(i.e. repeat formation test), especially for deeper wells(i.e. ＞2500 m in Fig.12), shear failure is likely to occur in the cement and needs to be considered for further operations.

(4) For injection operation, a large temperature difference between injection fluid and formation should be avoided.If injecting cold fluid is inevitable (e.g. offshore injection well in the North Sea), strong measures should be taken such as adding (additional) expanding additives into the cement system. Moreover, a higher injection pressure increases the compressive contact pressure at the cementformation interface, which can help to inhibit the debonding failure.

(5) The fluctuation of the cement temperature during hardening promotes the onset of shear and debonding failures. Since the numerical simulation of this process is based on a qualitative adaptation, representative quantitative measurements under downhole conditions are recommended.

6. Conclusions

The results of this study have shown that an MA initiates due to two major mechanisms that are related to loads during operations: (a) due to localized shear failure at the inner cement sheath induced by excessive inner casing pressure; and(b) due to debonding failure induced by injection-related cooling. It can be summarized that for shear failure due to excessive inner casing pressure, i.e. MA initiates at the casingcement interface, the poro-elastic bulk shrinkage coefficient(s) is the crucial factor, with the cement temperature fluctuations and pore pressure decrease during hardening also having significant influence. For tensile debonding failure at the cement-formation interface due to injection-related cooling,the poro-elastic bulk shrinkage coefficient (s) and the cement pore pressure decrease during hardening are the critical factors,and temperature fluctuation and simulating depth also have significant influences. The results documented in this study can raise awareness of predicting and evaluating MA under downhole conditions and can/should be used to supplement and improve future laboratory experiments.

Declaration of competing interest

The authors confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgments

The authors would like to thank Chevron ETC for financial support for this study.The authors are very grateful for the careful and constructive reviews by three anonymous reviewers, which greatly improved this contribution.

Appendices A-D. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2020.03.003.