Indirect determination of shear wave velocity in slow formations using full-wave sonic logging technique

Franiso Beltran, Alvaro Yañez-Gonzalez, María J. Crespo

a Belgar Engineering Consultants, Gabriel García Márquez 9, Collado-Villalba, 28400, Spain

b ESTEYCO, Menéndez Pidal 17, Madrid, 28036, Spain

c Principia Engineering Consuxltants, Velázquez 94, Madrid, 28006, Spain

Keywords:Sonic logging Slow formation Shear wave velocity Poisson’s ratio P-wave packet

A B S T R A C T This article presents a case study concerning a seismic characterization project. Full-wave sonic logging was used to characterize the shallow compressional wave and shear wave velocity profiles in the site.Anomalous values of the Poisson’s ratio derived from the velocity profiles suggested that the boreholes might have traversed slow formations (i.e. with shear wave velocity smaller than the borehole fluid compressional wave velocity or “mud-wave speed”) and that conventional processing of the sonic logs might have misinterpreted the direct arrivals of fluid acoustic waves as arrivals caused by shear wave propagation in the rock. Consequently, the shear wave velocity profiles provided by the contractor were considered to be unreliable by the project team. To address these problems, a non-conventional determination of the shear wave velocity was implemented,based on the relationship between the Poisson’s ratio of the rock formation and the shape of the first train of sonic waves which arrived to the receivers in the sonic probe. The relationship was determined based on several hundreds of finite element simulations of the acoustic wave propagation in boreholes with the same diameter as used in the perforations.The present article describes how this non-conventional approach was developed and implemented to obtain the shear wave velocity profiles from the raw sonic logs.The approach allows an extension of the range of applicability of full-wave sonic logging to determination of shear wave velocity profiles in formations with low compressional wave velocities. The method could be used to obtain shear wave velocity profiles where compressional wave velocity is as low as slightly larger than the mud-wave speed. A sample sonic log in Log ASCII Standard (LAS) format is provided as supplementary material to this paper via Mendeley Data, together with the FORTRAN source code used to process the log following the approach described in this study.

1. Introduction

The work described in this article originated from a seismic characterization project. Characterization normally requires the shallow shear wave velocity (VS) profiles to be defined, together with their range of uncertainty.Uncertainty in the VSprofiles can be reduced by site investigation campaigns using different geophysical techniques.

One of the techniques selected by the project was the full-wave sonic logging(Telford et al.,1991;Cogswell,2015).It is a relatively inexpensive technique,which operates in uncased boreholes filled with fluid.Basically,a sonic probe is lowered down to the bottom of the borehole using a winch.Then,the probe is raised at a constant speed while a transmitter in the probe sends sonic pulses at a constant time interval. The receivers mounted in the probe record the acoustic pressure signal produced by each of the pulses. From the processing of these records, compressional, shear and tube wave arrivals at the receivers are identified.Time differences allow for determination of the corresponding wave velocities.

The technique is normally considered to be adequate for investigation of compressional wave velocity (VP) and shear wave velocity (VS) profiles in medium to hard rocks. Particularly, the technique does not offer a direct determination of the shear wave velocity when this velocity is smaller than the mud-wave speed,that is, smaller than the compressional wave velocity in the fluid filling the borehole (Cheng and Toksöz, 1983; Stevens and Day,1986; Haldorsen et al., 2006). A formation whose shear wave velocity falls below the mud-wave speed is normally designated as a“slow formation” in the literature.

Note that the mud-wave speed is normally in the order of 1500 m/s. Hence, when the borehole crosses geological materials with VSsmaller than this value, care should be taken when processing the sonic logs,in order to avoid misinterpretation of mudwave direct arrivals (mud arrivals) as the ones caused by shear wave propagation in the rock. Misinterpretation normally leads to anomalous values of the Poisson’s ratio computed from interpreted VPand VS.

In the project which motivated the work described in this paper,conventional (semi-automatic) processing of the sonic logs produced anomalous values of the Poisson’s ratio at some horizons,with even negative values in some cases. This led to the suspicion that a slow formation could have been traversed and consequently,that the interpreted VSprofiles were not reliable. At the time this conclusion was reached, the boreholes had already been encased for performing other types of testing and therefore, using a different kind of suspension probe, which was more adequate for softer materials (e.g. P-S logging), was not possible.

For this reason,the project decided to explore the possibility of using the sonic logs to obtain an indirect estimate of VS.A literature review showed that the most popular approach to obtain such an estimate was based on the analysis of arrivals of the tube waves,designated by some authors as Stoneley waves (e.g. Stevens and Day, 1986). This approach required some significant lowfrequency content (<5 kHz) in the signal produced by the transmitter mounted on the sonic probe.Unfortunately,this was not the case and the arrivals of Stoneley waves were hardly identifiable in the sonic records.

As a consequence,an approach which was only suggested by the literature had to be explored:the correlation between the shape of the P-wave packet that arrives at the receivers and the Poisson’s ratio of the formation(Cheng and Toksöz,1983).The present article describes how this approach was developed and implemented to obtain the VSprofiles from the sonic logs.The authors could not find any previous implementation of the suggestion by Cheng and Toksöz (1983) in the literature. A sample sonic log in Log ASCII Standard (LAS) format is provided as supplementary material to this paper via Mendeley Data, together with the FORTRAN source code used to process the log following the method described in this article.

Even though the nature of the problem may be somewhat different,it should be mentioned that significant research has been carried out recently in the field of location of acoustic emission sources based on identification of compressional and shear wave arrivals to acoustic sensors (e.g. Dong and Li, 2013; Dong et al.,2019). This problem occurs in mining engineering, where safe exploitation requires prediction of large rockbursts from data gathered by a monitoring system. In that context, arrival times of compressional and shear waves have been used to calculate and fit the source location without the need for pre-measured wave velocity values (Dong and Li, 2013).

2. Description of the problem

2.1. Field work

Sonic logging was performed in boreholes with nominal drilling diameter of 96 mm and depths between 100 m and 150 m. The probe was a full-wave triple sonic probe manufactured by Robertson Geologging with diameter of 45 mm(RG,UK).It is a 2.45 m long probe,with a single transmitter and three receivers,located at 60 cm, 80 cm and 100 cm from the transmitter, respectively. After each shot of the transmitter, 512 samples were collected by each receiver, separated by an interval of 4 μs. Recorded data samples were sent to the RG Micrologger II console.

For performing the logging, the probe was descended into the borehole filled with fluid, up to the lowest point of interest. Then,the probe was lifted at a constant speed of 3 m/min.The transmitter sent a pulse every 1 cm, that is, every 0.2 s. Hence, the raw logs contained a sonic record at each of the receivers every 1 cm along the borehole.

Frequency set up in the transmitter of the probe was not reported by the contractor.It has been assumed that a 15 kHz acoustic pulse was used,which is considered to be a standard choice in this kind of field testing.

2.2. Processing of sonic probe records by the contractor

Velocity analysis performed by the contractor was based on the conventional“semblance processing”(Kimball and Marzetta,1984;Haldorsen et al., 2006). For VPprofiles, the contractor used the“adjust to extremum” algorithm, which looks for a maximum of coherence among signals at the receivers, combined with some manual picks to adjust the slowness diagrams.

2.3. Analysis of reported VP and VS profiles

For illustration purposes, Fig.1 shows a sample velocity profile reported by the contractor,corresponding to one of the boreholes,which crossed deposits from the Tertiary (sandstones and conglomerates, with some clay lenses). The blue and red lines represent VPand VS,respectively.Note that values of VSseem to be fairly constant at about 1500 m/s in most of the length of the borehole;in contrast, there were significant variations in VP. This was a first indication that the interpreted VSmight be associated with the fluid filling the borehole, rather than with the formation.

The Poisson’s ratio can be obtained from VPand VSusing the relationship between VP, VSand the Poisson’s ratio ν (see Eq. (1))(Shearer,1999).The resulting Poisson’s ratio profile was calculated from the velocity profiles and it is also shown in Fig.1.

The typical values of Poisson’s ratio for geologic materials are between 0.1 and 0.35 (Gercek, 2007); very seldom are values smaller than 0.05 or larger than 0.4 found. Therefore, the anomalous values on the profile shown in Fig.1b, especially the negative ones, were a strong indication that the borehole went through a slow formation and that sonic logs needed to be reinterpreted.After a lengthy interaction with the contractor, it was concluded that such a reinterpretation was not an easy task with the commonly used tools and the contractor decided not to investigate the anomaly further. This provided the motivation for the development of the methodology described in the following paragraphs.

3. Methodology

3.1. Theoretical background

3.1.1. Direct determination of compressional wave velocity (VP)

Fig.1. (a) Sample velocity profiles reported by the contractor and (b) Poisson’s ratio profile derived from them.

Fig. 2 shows a sample of sonic records at the three receivers of the full-wave triple sonic probe used by the contractor.The arrows mark the first arrivals at the receivers, which correspond to the compressional wave propagated in the formation at speed VP, that is, the refracted head wave propagated along the formation-fluid interface at speed VP(Haldorsen et al., 2006).

If the times of these first arrivals to the closer, middle and farther receivers are designated as tC,tM,tF,respectively,then,from the known distance between receivers (Δz = 20 cm), up to three estimates of VPvelocity can be obtained as follows:

3.1.2. Influence of formation Poisson’s ratio on the sonic logs in a slow formation

Fig. 3 shows a schematic of the different waves arriving at a receiver during a typical sonic probe test in a slow formation. The first arrival of waves, that corresponds to the so-called P-wave packet, is large in amplitude, relatively monochromatic, and with long duration.Afterwards,the direct fluid(mud)wave arrives,with speed of about 1500 m/s. Finally, the Stoneley wave comes in,which has a smaller frequency.

As early as in 1983, researchers realized that the amplitude and duration of the P-wave packet were sensitive to the Poisson’s ratio in the rock formation(Cheng and Toksöz,1983).The amplitude of the Pwave packet was found to be roughly proportional to the Poisson’s ratio of the formation(Fig.4).The analytical relationship between the amplitude of the P-wave and the Poisson’s ratio was not reported.

Thus,in cases where the Stoneley waves are hard to identify,the amplitude of the P-wave packet could be used to provide an estimate of the Poisson’s ratio.Direct determination of VP(see Section 3.1.1) and evaluation of the Poisson’s ratio allow for an indirect determination of VSin the rock formation.

3.1.3. Correlation of P-wave shape and Poisson’s ratio

In this work,the correlation of the P-wave packet shape and the formation Poisson’s ratio was obtained empirically using a battery of finite element analyses.For this purpose,a finite element model of a 100 mm diameter borehole filled with fluid was developed.The model is shown in Fig. 5. The model takes advantage of the axial symmetry of the problem. Hence, it is a two-dimensional (2D)model. The formation was assumed to be homogeneous and isotropic, with properties varying within the limits shown in Table 1.

Fig.2. Sample of sonic record at receivers 1,2 and 3.Arrows indicate first wave arrivals at each receiver. Amplitudes are given as arbitrary units.

The fluid was modeled as an acoustic medium, with density of 1200 kg/m3and VPof 1.4 km/s. Attenuation in the fluid was introduced by a quality factor Qfof 25 (Gibowicz and Kijko,1994;Cheng and Toksöz, 1983). Pressure pulse produced at the transmitter was modeled using a 15 kHz Ricker wavelet (Wang, 2015;Toksöz et al., 1983), with a maximum amplitude of 10 kPa. The shape of the P-wave packet was not dependent on the selected maximum amplitude.

Analyses were carried out using ABAQUS/Explicit v. 6.14-2(Dassault Systèmes Simulia, 2013). A sample input file for a particular set of properties of the formation has been provided as supplementary materials at the end of this article.

Fig.6 shows the sonic pressure at the first receiver computed for different Poisson’s ratios,at a constant compressional wave velocity of 1650 m/s and density of 2000 kg/m3in the formation. The sensitivity of the signal to Poisson’s ratio was confirmed by the analyses.Note that the artificial signals had three initial peaks.The first peak(Peak 1)was negative,with small relative amplitude.The second (Peak 2) was positive, with medium relative amplitude.Finally, the third (Peak 3) was negative, with large relative amplitude.

In the sonic logs coming from the field, the first peak is sometimes difficult to identify,due to the relatively low resolution of the records(one point every 4 μs)and the signal-to-noise ratio(SNR)of the signal.Hence,it was decided to use a shape factor based on the other two peaks to correlate the P-wave packet shape with the Poisson’s ratio.

Fig. 3. Schematic of a typical sonic record in a slow formation, showing arrival of the P-wave packet, the sonic wave transmitted directly by the borehole fluid and the Stoneley wave propagated along the formation-fluid interface. Adapted from Cheng and Toksöz (1983).

After some trials with other possibilities, the shape factor that showed best results was

where P2and P3are the (algebraic) amplitudes at Peak 2 and Peak 3, respectively. Since the time interval between the two peaks was fairly constant with varying Poisson’s ratio, the selected shape factor is a dimensionless approximation to the average absolute value of the derivative of the signals between Peak 2 and Peak 3.

Fig. 5. Finite element model used in the computation of P-wave packet shape factor(SF).

Once the shape factor was selected,i.e.Eq. (3),a series of finite element analyses was used to define the dependence between the Poisson’s ratio, compressional wave velocity, shape factor and the mass density of the formation material, within the ranges defined in Table 1.Results are presented in Table 2 and graphically in Fig.7.Values given in the table are for the first receiver(60 cm away from the transmitter) and a density of 2000 kg/m3in the formation.Differences with values computed for other densities(e.g.1900 kg/m3and 2200 kg/m3) are smaller than 5% for VPvalues larger than 1700 m/s.

It can be seen from Table 2 that the Poisson’s ratio ν is basically proportional to the selected shape factor (SF) for compressional wave velocities (VP) above 2000 m/s, as suggested by Cheng and Toksöz (1983). For the first receiver, a good linear correlation for 2000 m/s < VP< 3000 m/s and the present borehole diameter(100 mm) is given by

with a coefficient of determination (R2) of 0.989.

Similar correlations may be obtained for the other two receivers of the probe. However, the first receiver was used since its signal was stronger(better SNR).

3.1.4. Indirect determination of shear wave velocity (VS)

Indirect determination of shear wave velocity (VS) is based on the direct determination of the compressional wave velocity (VP)(see Section 3.1.1) and of the shape factor (SF) (see Section 3.1.3)from the sonic log. Using these two values, an estimate of the Poisson’s ratio can be obtained from the correlation in Table 2.Then, shear wave velocity is estimated using the well-known expression (Kramer,1996):

3.2. Processing of raw records

The listing of the FORTRAN program used for processing the records is provided in the supplementary materials. An overall description is provided in the following sections. Fig. 8 shows the general workflow.

3.2.1. High-pass filter

For each record,the first step of the processing was elimination of the Direct Current (DC)-Offset, which appeared in the time histories as a constant reference value different from zero.A high-pass filter, with a cut-off frequency of 1 kHz was used.

3.2.2. First arrival times

After elimination of the DC-Offset, the next step was determination of the first arrival times.The problem was addressed by the identification of Peak 1, Peak 2 and Peak 3 in each of the records(see Fig.6).Each of these peaks had an arrival time and amplitude of the signal.

Table 1 Range of variation of formation properties used to compute P-wave packet shape factor.

Fig. 6. Artificial signals computed at the receiver closest to the transmitter, for different Poisson’s ratios.

Table 2 Computed shape factors(SF)as a function of Poisson’s ratio(ν)and compressional wave velocity(VP).Values given in the table are for the position of the first receiver(60 cm away from the transmitter)and a density of 2000 kg/m3 in the formation. Nominal diameter of borehole is 100 mm.

Peak 1 (the first one) had usually a very small amplitude when compared with the other two. In the records provided by the contractor,probably due to the small time-resolution and SNR,this peak was the most difficult one to be identified; and for many times, it was masked by the noise of signals. The strategy was to identify Peak 3 at first. Peak 3 is the largest one. Once Peak 3 was identified, Peak 2 was found by going back in time until the peak was found.Peak 3 can be easily distinguished from noise by setting a numerical threshold.

3.2.3. Compressional wave velocities

Once Peak 2 and Peak 3 were identified for the three receivers,estimates of compressional wave velocity (VP) were computed using Eq. (2).

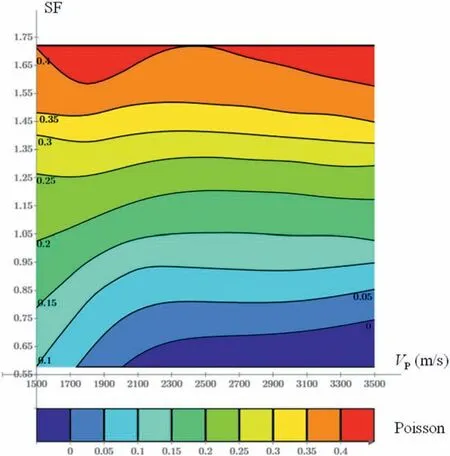
Fig.7. Contours of Poisson’s ratio as a function of shape factor(SF)and compressional wave velocity (VP, unit: m/s). Values are for a density of 2000 kg/m3 in the formation.

No semblance analysis was performed, which perhaps could have improved the accuracy of estimates. However, note that the probe had only three receivers,which is in the lower limit to apply the semblance analysis. Hence, a low-quality signal at any of the receivers could prevent the semblance analysis from being performed or, if performed, it could produce misleading results.

3.2.4. Poisson’s ratio

Using the amplitudes at Peak 2(P2)and Peak 3(P3)at each of the three receivers, three SF values can be obtained for the signal at each receiver using Eq. (3).

The SF value for the first receiver was selected for computation of the Poisson’s ratio, since it was at the first receiver where the signal was stronger.From this shape factor,the Poisson’s ratio was obtained by linear interpolation using the values given in Table 2.

3.2.5. Shear wave velocities

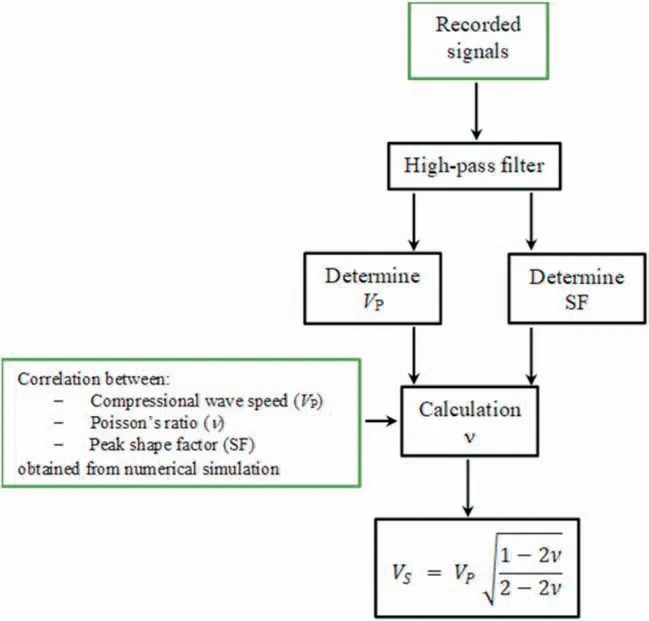
Fig. 8. Flowchart of the proposed indirect shear velocity calculation method.

Fig.9. Poisson’s ratio derived from P-wave packet shape factors and resulting reprocessed velocity profiles(values averaged over 50 cm):(a)Compressional and shear wave velocity profiles, and (b) Poisson’s ratio profile.

Shear wave velocity (VS) was obtained from VPand ν, using Eq.(5). Note that shape factors given in Table 2 were computed for a formation mass density of 2000 kg/m3.However,the actual value of the density along the boreholes was not measured. The authors judged that the density along the boreholes would be 1900-2200 kg/m3.Variation of the shape factors within these limits of the density was determined to be small and could be bounded by an error of ±5%.

Using the approximate correlation given by Eq.(4),a 5%change in the shape factor leads to 2% (= 5% × 0.409) change in the Poisson’s ratio.For Poisson’s ratios between 0.2 and 0.35,a variation 2%of the Poisson’s ratio produces a change in the shear wave velocity(VS)between 1.2%and 2.5%of the compressional wave velocity(VP).This was considered to be an acceptable increase of uncertainty,given the current constraints for the indirect determination of VS.

4. Results

4.1. Sample raw records from sonic logging

A sample raw sonic logging set of data has been provided as supplementary materials so that the interested reader could reproduce the results given in the following section. The raw data set was the one processed by the contractor to obtain the profiles as shown in Fig.1.It corresponds to just one of the boreholes used in the characterization project.

The set of raw data in the supplementary materials has been provided as a file with LAS format, which can be opened by a regular text editor.After some descriptive lines,the file contains three blocks of data, corresponding to the closest receiver (60 cm), the most distant receiver (100 cm), and the intermediate receiver(80 cm), respectively. Within each of these blocks, each line contains the complete time history of acoustic pressure at a certain depth. The line has 513 numerical values. The first value is the depth at which the record was taken, and the other values correspond to the amplitudes of the sonic record at a 4 μs time step.Origin of depths was always the ground surface and there was a record every 1 cm of depth.

4.2. Reprocessed profiles

Fig.9 shows the Poisson’s ratio profile obtained for the selected borehole, computed from the compressional wave velocity (VP)directly derived from the sonic log and the sonic wave shape factor,as described in Section 3.2.Fig.9 also gives the compressional wave velocity (VP) and the shear wave velocity (VS) profiles obtained using the new method presented in Section 3. The differences between the profiles in Fig. 9 and the ones initially estimated by the contractor for the same borehole (see Fig.1) are apparent:

(1) The values of Poisson’s ratio are now within the range of 0.19-0.22, basically all along the depth, which are well within the range expected for geologic materials and also fall within the range where the regression by Eq. (4) is reasonable.

(2) VPand VSprofiles are now relatively parallel, which corresponds to a fairly constant Poisson’s ratio with depth.

(3) VPprofiles in Figs.1 and 9 are relatively similar, that is, the approach described in this article produces a compressional wave velocity profile consistent with the one obtained by the conventional approach used by the contractor.

(4) VSresulting from the reprocessing (Fig. 9) are between 1000 m/s and 1500 m/s along significant portions of the profile, which suggests that the borehole indeed crossed slow formations. Comparing Figs. 1 and 9, it is noted that anomalous Poisson’s ratios in Fig.1 correspond to stretches along the borehole with VSvalue smaller than 1500 m/s in Fig. 9.

5. Conclusions

Within a seismic characterization project, an optimistic assumption about the shear wave velocity (VS) values at the site motivated selection of the full-wave sonic logging technique.This technique cannot provide a direct measurement of the shear wave velocity profile when the velocities are smaller than about 1500 m/s.

The Poisson’s ratio profiles obtained from the VPand VSprofiles provided by the contractor showed anomalous values, which suggested that the boreholes were crossing slow formations, that is,horizons with VSsignificantly smaller than 1500 m/s.Hence,the VSprofiles provided by the contractor were considered to be unreliable by the project team.

An approach for indirect determination of the VSwas developed and implemented. The approach was inspired by seminal work performed in the 1980s,which identified a connection between the formation’s Poisson’s ratio and the wave shape of the first train of acoustic waves(P-wave packet)reaching the receivers(Cheng and Toksöz,1983).In the present work,this connection was determined empirically, using finite element simulation, for the particular conditions of the project, such as the borehole diameter and the sonic probe configuration.

Reprocessing of the raw sonic logs using the newly developed approach produced VSprofiles that were consistent with those obtained using other geophysical techniques. Therefore, sonic logging results could eventually be used to reduce the uncertainty levels in the shallow shear wave velocity profiles, as originally intended by the project.

On the other hand, the new approach produced compressional wave velocity (VP) profiles that were consistent with those calculated by the contractor using the conventional approach.Hence,the new calculation of VPvalues would not be strictly necessary:the VPvalues provided by the contractor could have been directly used.

For the conditions of the project, particularly for the configuration of the sonic probe used in the field work, practical application of the approach presented in this paper extends to compressional wave velocities VPin the formation as low as 1600 m/s. For smaller VP, the initial P-wave packet becomes distorted by the direct arrival of the acoustic wave travelling through the fluid. For the common range of Poisson’s ratio in geological materials, this means that the approach can be used for indirect determination of shear wave velocities VSas small as 750-900 m/s.This allows extending somewhat the usual domain of application of the full-wave sonic logging technique.

This work was performed within the time limits of an industrial project. Additional research would be necessary for potential refinement and generalization, for example, to other borehole diameters or other sonic probe designs.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2020.05.009.