Influence of degree of interlock on confined strength of jointed hard rock masses
Navid Bahrani, Peter K. Kaiser
a Department of Civil and Resource Engineering, Dalhousie University, Halifax, Nova Scotia, Canada
b Bharti School of Engineering, Laurentian University, Sudbury, Ontario, Canada
Keywords:Rock mass strength Degree of interlock Non-persistently jointed rock mass Blocky rock mass Geological strength index (GSI)GSI strength equations
A B S T R A C T The strength of jointed rock mass is strongly controlled by the degree of interlock between its constituent rock blocks.The degree of interlock constrains the kinematic freedom of individual rock blocks to rotate and slide along the block forming joints. The Hoek-Brown (HB) failure criterion and the geological strength index (GSI) were developed based on experiences from mine slopes and tunneling projects in moderately to poorly interlocked jointed rock masses. It has since then been demonstrated that the approach to estimate the HB strength parameters based on the GSI strength scaling equations(called the‘GSI strength equations’)tends to underestimate the confined peak strength of highly interlocked jointed rock masses (i.e. GSI >65), where the rock mass is often non-persistently jointed, and the intact rock blocks are strong and brittle. The estimation of the confined strength of such rock masses is relevant when designing mine pillars and abutments at great depths, where the confining pressure is high enough to prevent block rotation and free sliding on block boundaries. In this article, a grain-based distinct element modeling approach is used to simulate jointed rock masses of various degrees of interlock and to investigate the influences of block shape,joint persistence and joint surface condition on the confined peak strengths. The focus is on non-persistently jointed and blocky (persistently jointed)rock masses, consisting of hard and homogeneous rock blocks devoid of any strength degrading defects such as veins.The results from this investigation confirm that the GSI strength equations underestimate the confined strength of highly interlocked and non-persistently jointed rock masses. Moreover, the GSI strength equations are found to be valid to estimate the confined strength of persistently jointed rock masses with smooth and non-dilatant joint surfaces.
1. Introduction
The unconfined compressive strength (UCS) of jointed rock masses is an important parameter for design of underground excavations, especially when dealing with rock failure and support design near excavation boundaries,where the confining pressure is relatively low. Good knowledge of the strength of jointed rock masses at elevated confining pressures becomes relevant when designing wide pillars and mine abutments at great depths, or when using continuum numerical models for simulating largescale problems, where the failure envelope of the jointed rock mass for a wide range of confinements is required.
Bahrani and Kaiser(2013)and Bewick et al.(2019)discussed that conventional approaches for rock mass strength estimation, which were originally established for design of excavations in heavily jointed rock masses,are flawed when applied without modification to massive and moderately jointed hard rock masses. For example,the geological strength index (GSI) (Hoek,1994; Hoek et al.,1995)used to characterize jointed rock masses and estimate the Hoek-Brown (HB) strength parameters (Hoek and Brown, 1997, 2019;Hoek et al., 2002) was developed based on experience from mine slopes and near-excavation behavior of tunnels (i.e. engineering problems at low confinement)in heavily jointed and relatively weak rock masses.The application of these approaches for estimating the confined strength of jointed rock masses has been successful when the rock mass conforms to conditions used to develop them.However, these approaches are limited when dealing with nonpersistently jointed hard rock masses, when rock blocks cannot form,rotate or slide without failure through intact rock.
The focus of this article is on the confined strength of nonpersistently jointed and blocky rock masses consisting of hard,brittle and homogeneous blocks devoid of strength degrading defects such as veins. Such rock masses are typically classified with GSI values greater than 65(Cai et al.,2004).A grain-based distinct element model, previously calibrated to the laboratory properties of intact and heat-treated marbles, is used to investigate the influence of degree of interlock on the confined strength of rock mass.The heat-treated marble serves as an analogue for a highly interlocked jointed rock mass. The grain-based model is then modified to simulate a well interlocked blocky rock mass. The influences of joint persistence and joint frictional strength, as the factors contributing to the degree of interlock and rock mass strength,are also investigated on both rock mass models.
The results presented in this context confirm the limitations of the GSI strength scaling equations (called the ‘GSI strength equations’) for estimating the confined strength of non-persistently jointed and blocky hard rock masses, suggesting a need for a revised approach when dealing with such rock masses under highly confined conditions.
2. Historic development of the Hoek-Brown failure criterion and the GSI system
The HB failure criterion was developed by Hoek and Brown(1980) to capture the nonlinear failure envelope of intact rock and rock masses for design of underground excavations in jointed rock masses that can be represented by a homogeneous and isotropic material model.The rock mass strength(σ1)using the HB failure criterion in its generalized form is a function of confinement(σ3) according to the following equation:

where σciis the uniaxial compressive strength of the intact rock,mbis a reduced value of the intact rock parameter mi, and s and a are the material constants. The values of miand σciare obtained by statistical fit to peak strength data within a confinement range of 0 to 0.5UCS,where UCS is the intact rock strength obtained directly from laboratory unconfined compression tests. The empirical constants mband s are related to the angle of internal friction of the rock mass and its cohesive strength. The constant a controls the curvature of the failure envelope.It is typically near 0.5 for high GSI values(>55)and reaches 0.6 for extremely poor ground.Hoek and Brown (1997) emphasized that the parameter recommendations for the HB failure criterion are based on sparse data and therefore are intended to serve as rough guides in preliminary design calculations. They emphasized that every attempt must be made to determine the required strength parameters by laboratory and in situ testing and by in situ observations of the full-scale performance of the rock mass around excavations.
The concept and early developments of the HB failure criterion are based on the laboratory strength data of intact and jointed Panguna andesites (Hoek and Brown,1980), from the Bougainville open pit copper mine in Independent State of Papua New Guinea.Professor Hoek became involved in this project in the early 1980s in association with a project on rock slope stability at Imperial College of Science and Technology, UK. He visited the mine several times over the years as a consultant until the mine was abandoned in the late 1980s as a result of civil war in the Solomon Islands. These islands are in a very active earthquake belt between Japan and New Zealand. As a result of its tectonic history, the Panguna andesite consists of strong and brittle rock (mean UCS of 265 MPa) but is heavily jointed with rock blocks typically measuring 50-200 mm(Fig.1a).
Dr.John Read was a superintending geotechnical engineer at the mine for a large part of its short life and was able to provide detailed descriptions of the geology of the andesites and granodiorites in which the open pit was mined. The challenge at the time was to arrive at rational method for designing 1000 m high slopes in this very heavily jointed rock mass.This was tackled by Professor Hoek,in association with Dr.John Bray and David Pentz and a number of graduate students,including Peter Cundall,John Sharp,Nick Barton and others (Hoek, personal communication, 2011).
The basic decision was to treat the rock mass as a compacted rockfill and to design the slopes using available limit equilibrium methods.At this time,the rock mechanics group at Imperial College worked very closely with the soil mechanics group (Professors Skempton and Bishop) and used the slope stability software developed by Morgenstern and Price (1965). In order to estimate the strength of the rock mass, specimens of rock from bench faces were gathered by a front-end loader,dumped into large drums and transported to the Snowy Mountains Laboratory in Cooma,Australia. There they were compacted as much as possible into a 1 m diameter rockfill triaxial cell (Fig.1b) and tested.
At a later stage in the project,Bougainville mine constructed its own smaller rockfill triaxial cell and carried out tests on site(Fig.1c).Professor John Jaeger of the Australian National University in Canberra was also engaged as a consultant by the Bougainville mine and arranged for small specimens of intact andesite and 150 mm diameter core of closely jointed andesite to be transported to his laboratory.The 150 mm diameter cores were wrapped in thin copper foil and then tested in triaxial compression.Fig.2a presents the laboratory test results and initial analyses made during the development of the HB failure criterion in the early 1980s (Hoek,personal communication, 2011).
Hoek and Brown(1980)presented the HB parameter s and the ratio mb/mi(on a logarithmic scale)as a function of the rock mass classification parameters RMR and Q for various categories of Panguna andesite specimens(Fig.2b).They found the best fit line to the strengths of intact and jointed Panguna andesite to provide approximate relationships between s and mb/miand the classification ratings. In Fig. 2b, the jointed andesite covers low RMR and Q values representing weak and poorly interlocked rock masses. As can be seen from this figure, there was no data available for RMR values greater than 50 or Q values greater than 4 (i.e. fair to extremely good rock masses). The functional relationship was anchored at the intact rock strength for RMR = 95 and Q = 400.
Based on the concepts developed at Bougainville and geotechnical engineering experience from slope stability and tunneling projects since then, Hoek et al. (1995, 2002) proposed strength equations based on the GSI system for estimating the unconfined and confined strengths of jointed rock masses of varying qualities.The rock mass strength parameters mb,s and a are functions of the GSI value and can be determined using the following equations(GSI strength equations):

where D is a factor to account for excavation disturbance related to blast damage in the immediate vicinity of excavation walls. It ranges from 0 to 1 to cover the range of undisturbed ground as encountered in mechanically excavated underground openings(i.e.D = 0) to disturbed ground(i.e. D = 1).

Fig. 1. (a) Drs. John Read and Kevin Rosengren examining a typical bench face in jointed andesite of the Bougainville mine; (b) Rockfill triaxial cell, for testing 1 m diameter specimens, in the Snowy Mountains Laboratory in Cooma, Australia; and (c) Rockfill triaxial cell, for testing 0.5 m diameter specimens at the Bougainville mine site.
According to Hoek and Brown (2019), the GSI system was developed to estimate the strength of rock masses comprised of interlocking angular blocks, in which the failure process is dominated by block sliding and rotation without a great deal of intact rock failure(i.e.GSI values less than 65).Bahrani and Kaiser(2013)investigated the applicability of the GSI strength equations for estimation of confined strength of jointed andesite.First,they fitted the HB failure envelope to the intact strength of andesite(GSI=100,Fig.3a),and then reduced the GSI values,in increments of 10 from 90, until the strength of jointed andesite was matched. Fig. 3a shows that both the unconfined and confined strengths of the jointed rock mass decrease as the GSI value decreases from 100 to 10. The minimum and maximum strengths of heavily jointed andesite are bound with the GSI values of 10 and 30, respectively(Fig. 3b). The strength of the recompacted specimens can be approximated with GSI = 2 (Fig. 3c). Note that a GSI value of 2,which is out of the range of applicability of the GSI strength equations, was chosen to match the strength of the recompacted andesite under an unconfined condition.According to Hoek(1998),such a precise GSI value to estimate the strength of a jointed rock mass is not realistic.It can be seen from Fig.3 that the values of the constants m and s decrease from the intact andesite (i.e. mi= 24 and s=1 for GSI=100)to those of jointed andesite(i.e.mb=0.96 and s = 0 for GSI = 10). The equivalent friction angle or slope of a Mohr-Coulomb fit for the jointed andesite ranges from 24°to 30°(not shown in Fig. 3b).
The analysis conducted above demonstrates how the rock strength decreases with increasing specimen size and confirms that the GSI system provides a reliable means of estimating the confined strength of 150 mm diameter heavily jointed andesite and 1 m diameter highly compacted rockfill specimens from standard laboratory-scale specimens of intact andesite. The results of this analysis are consistent with those of previous studies, confirming that the HB failure criterion and the GSI strength equations provide a reliable approach for estimating the strength of moderately to heavily jointed rock masses,represented by GSI values less than 65(e.g. Diederichs et al., 2007; Brown, 2008; Carter et al., 2008;Eberhardt, 2012). It also suggests that the GSI approach to obtain rock mass strength parameters was developed on weak rock masses having a UCS of nearly zero,although the intact rock is very strong.
It will be demonstrated next, based on the numerical results of jointed rock masses,that the GSI strength equations underestimate the confined strength of non-persistently jointed hard rock masses.
3. Factors influencing degree of interlock in a jointed rock mass
According to Hoek and Brown (1980), the strength of a jointed rock mass is controlled by the degree of interlock,which describes the kinematic freedom of individual rock blocks to rotate and slide along each other.The higher the degree of interlock,the larger the rock mass strength. Unfortunately, the degree of interlock cannot be quantified but the blockiness and joint surface conditions are related to the degree of interlock. Terzaghi (1946) and others,including Bieniawski (1989) and Barton et al. (1974), have used these parameters for the rock mass classification systems RMR and Q, respectively. Hoek (1994) and Hoek et al. (1995) adopted them for the development of the GSI system and, most importantly, for strength estimation of jointed rock masses of various qualities.The degree of interlock in the GSI chart is controlled by the geometric shape of the rock blocks (i.e. vertical axis in the GSI chart, Fig. 4).The most interlocked rock mass in Fig.4(after a massive rock mass)is a blocky rock mass that consists of undisturbed rock blocks formed by three orthogonal persistent joint sets. The least interlocked rock mass is a disintegrated rock mass that consists of a mixture of angular and rounded rock pieces.
The following review summarizes the main factors contributing to the degree of block interlock including block shape, block size,joint orientation, joint surface condition, joint persistence, and block strength:
(1) Block shape. Rock masses in terms of block shape are classified as massive, blocky, tabular, columnar, irregular, and crushed. The number of joint sets and their orientations define the shape of the blocks (ISRM,1978). The geometric shape of the blocks contributes to the degree of interlock in a jointed rock mass. In a complex shaped block assembly, the geometric incompatibilities between the blocks inhibit them from rotating or sliding. Particularly, convex block shapes contribute to interlock. If deformed, this leads to geometric dilation or a bulking process that must precede failure. A high(geometric)dilation leads to a steep failure envelope at low confinement, resulting in a rapid increase in the rock mass strength with increasing confinement (Bahrani et al.,2014).

Fig. 2. (a) Plot of the results of Bougainville tests on andesite compacted rockfill and Jaeger’s tests on 150 mm diameter core of jointed andesite (from Dr. Hoek’s personal notes); and (b)s and mb/mi values for the Panguna andesite plotted against rock mass classification parameters RMR and Q (after Hoek and Brown,1980).
(2) Block size.The size of blocks also contributes to the degree of interlock. The number of joint sets, joint spacing, and joint persistence determine the block size(ISRM,1978;Kim et al.,2007).Rock masses composed of large blocks tend to be less deformable and develop arching and interlock in underground openings (ISRM, 1978). Rock masses consisting of small rock blocks tend to fail due to block rotation.Therefore,the larger the blocks, the higher the degree of interlock and the rock mass strength.
(3) Joint orientation. The orientation of joints relative to the loading direction controls the freedom of rock blocks to slide and rotate and therefore the degree of block interlock in a jointed rock mass. Singh et al. (2002) and Huang et al.(2019) identified four distinct modes of failure from the results of physical models and numerical simulations of jointed rock masses consisting of two perpendicular joint sets (in two dimensions): tensile failure and splitting of intact rock blocks,shearing of intact rock blocks,rotation of rock blocks and sliding of rock blocks along joints. The observed failure modes are attributed to the orientation of joints relative to the loading direction and associated degree of interlock. Sliding of rock blocks along joints and block rotation are the main modes of failure if the joints are critically oriented(i.e.joint parallel to 45°+φ/2,where φ is the joint effective friction angle), as was also observed in laboratory tests by Ladanyi and Archambault(1970).A rock mass with joint sets oriented sub-parallel or sub-perpendicular to the loading direction presents a higher strength because failure is largely controlled by the strength of intact rock blocks.In such rock masses,the strength envelope increases nonlinearly with increasing confinement, whereas those with critically oriented joint sets represent purely frictional behavior (i.e. linear failure envelope) with no or very small initial dilation and a comparatively low cohesive strength(Hoek,1983).
(4) Joint surface condition. The non-planarity of discontinuities(roughness and waviness)contributes to the degree of block interlock. The surface roughness decreases the ability of blocks to slide and rotate during the failure process by increasing the area of contact between blocks, limiting the kinematic freedom at the block surface scale. Based on Patton (1966)’s bilinear shear strength envelope for rough discontinuities, the dilational characteristics due to roughness lead to a rapid increase in normal stress and thus shear strength. Beyond a critical normal stress, dilation is suppressed, and failure occurs by shearing off the asperities.Considering the intact rock and the rough joint in the Patton’s rock-joint system as an analogue for rock blocks and rough block boundaries (i.e. discontinuities), Bahrani and Kaiser (2017) discussed that at low confinement (σ3< UCS/10),failure occurs mainly along the block boundaries causing geometric dilation and resulting in a steep failure envelope represented by a high equivalent friction angle (i.e. basic friction angle plus dilation angle). Beyond this confining pressure threshold (σ3>UCS/10), the sliding along block boundaries is inhibited and failure occurs by breaking through the rock blocks or at least block corners,resulting in a shallower failure envelope.
(5) Joint persistence.Persistence defines the areal extent or size of discontinuities.According to ISRM(1978),persistence can be crudely quantified by measuring the trace lengths of discontinuities on exposed surfaces. The joint persistence K is defined by Einstein et al. (1983) as

where JL is the length of a joint segment,and RB is the length of the rock bridge between two joint segments.
Joint persistence influences, and when non-persistent,dominates the failure process and thus the degree of interlock and rock mass strength. The presence of rock bridges forces failure through intact rock and highly restricts rock blocks from sliding or rotating. Rock bridges have to fail before any sliding or rotation is possible and this has a major influence on the strength of non-persistently jointed rock masses,particularly with strong intact rock.At low confining pressures, unstable tensile crack or fracture propagation leads to wing crack formation within the rock bridge from the tips of pre-existing discontinuities. With increasing confining pressure, tensile crack formation is constrained,and unstable propagation is inhibited.Hoek and Bieniawski(1965)showed that the length of crack propagation from the tips of a pre-existing crack is highly dependent on the confining pressure. They found that the crack length under triaxial compression is sensitive to the ratio of σ1/σ3,and its extension reduces to less than 10% of its original length for confining pressures greater than about 10% of the applied major principal stress. This means that much higher loads are required before damage can be accumulated in a rock at high confinement (σ3>0.1σ1) than at low confinement(σ3< 0.1σ1).
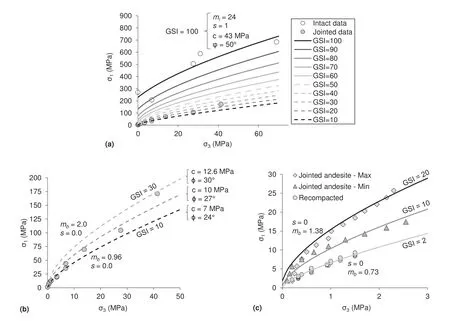
Fig. 3. (a) Strengths of intact and jointed andesites (tested by Jaeger,1970) and the HB failure envelopes for GSI values ranging from 100 to 10; (b) Closer view of the strength of jointed andesite bound with GSI values of 10 and 30; and (c) Strengths of recompacted rockfill and jointed andesite specimens tested by Bougainville copper mine and corresponding strength envelopes with GSI values of 2,10 and 20.
(6) Rock block strength.The strength of a rock block is influenced by the strength of the intact part of the block as well as the strength of discrete defects (e.g. veins) within a block. In a highly interlocked jointed rock mass at low confinement,the high rock block strength causes geometric dilation, resulting in a rapid increase in the confined strength and thus a steep failure envelope. At high confinement, this dilation is constrained and, by analogue to Patton (1966)’s experiments (as explained above), a bilinear strength envelope emerges, as failure occurs by shearing through the rock blocks. If the blocks are weak, the rock mass can easily fail by shearing through the rock block at low confinement and this reduces the initial dilation.Therefore,the increase in the strength of a jointed rock mass consisting of weak rock blocks is more gradual with increasing confinement, resulting in a lower strength at high confinement than that of a rock mass consisting of strong rock blocks. In this respect, the presence of strength degrading defects (e.g. veins) can contribute to the strength and failure mode of rock blocks,and therefore jointed rock masses(Pierce et al.,2009;Day et al.,2019).
4. Analogues for highly interlocked jointed rock masses
A highly interlocked jointed rock mass consists of hard brittle rock blocks and joints that are rough and non-persistent. Kaiser et al. (2011), Valley et al. (2011) and Bahrani (2015) hypothesized that the confined strength of a highly interlocked jointed rock mass is much higher than that obtained from common empirical approaches(e.g.GSI system). Unfortunately, data for back analysis of rock mass strength,especially at high confinement,are limited and conducting in situ experiments to back analyze rock mass strength requires extensive investment and planning.Conducting laboratory tests on large-scale rock mass specimens is expensive and timeconsuming and, furthermore, most facilities cannot test largescale hard brittle rocks at high confining pressures. Therefore,knowledge and understanding of the behavior and strength of highly interlocked rock masses under a wide range of confining pressures require conducting laboratory tests on physical models(Brown,1970;Brown and Trollope,1970)or analogues (Rosengren and Jaeger,1968; Gerogiannopoulos,1976; Gerogiannopoulos and Brown, 1978) for such rock masses. The following sections provide a review of published laboratory tests on analogues for highly interlocked jointed rock masses.
4.1. Granulated marble
Rosengren and Jaeger (1968) and Gerogiannopoulos (1976)found that if intact Wombeyan and Carrara marble specimens are heated to 600°C, the anisotropy of thermal expansion of calcite crystals causes separation of the grains at their boundaries. This results in the generation of a highly interlocked but weakened material,which is referred to as granulated marble.The granulated marble with randomly oriented grain boundaries and nearly zero tensile strength is considered an analogue for a highly interlocked and non-persistently jointed rock mass (Bahrani and Kaiser, 2013;Bahrani et al.,2014).
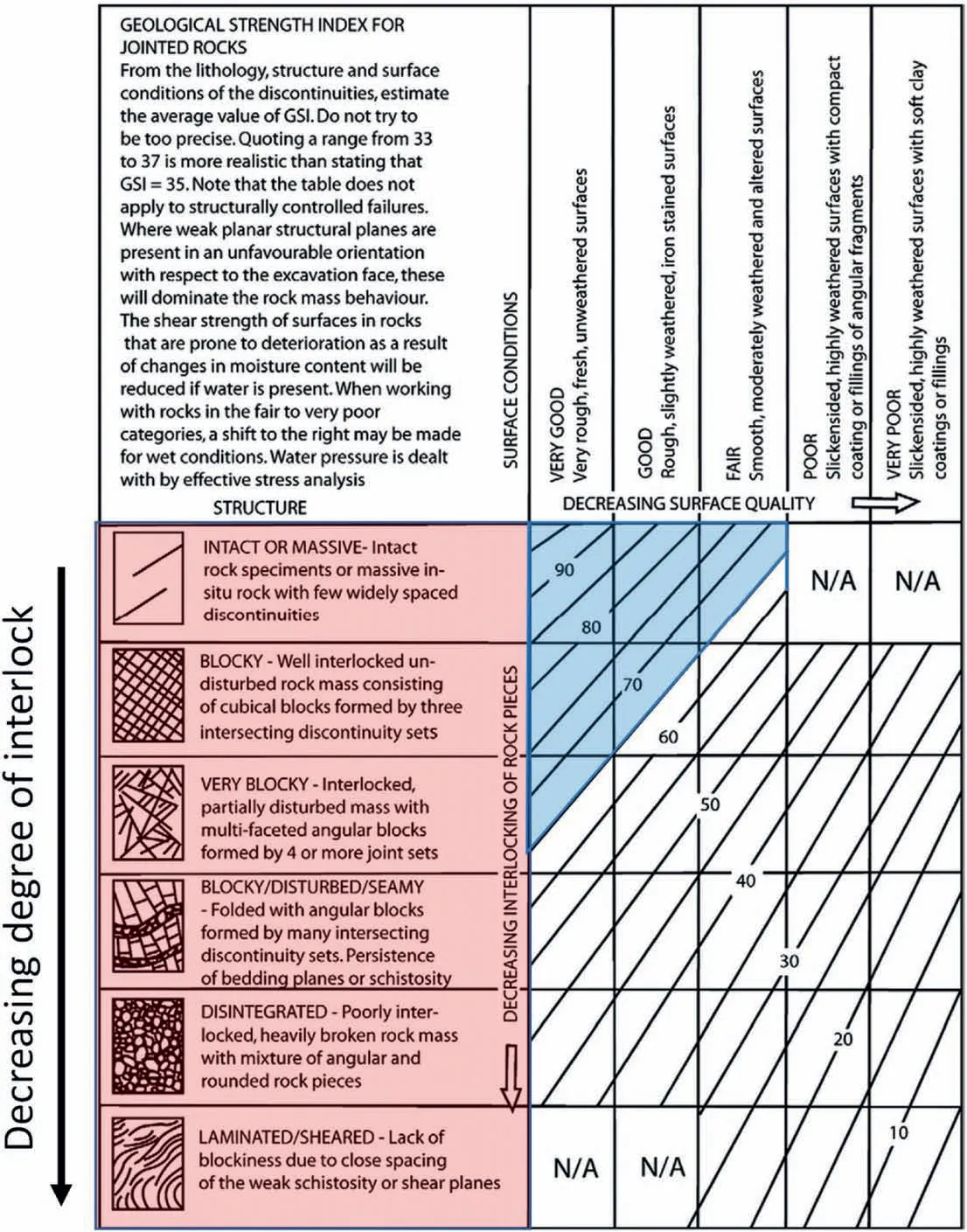
Fig.4. The GSI chart highlighting different rock mass structures,representing various degrees of interlock.The area with GSI >65 is highlighted in blue(after Hoek and Brown,1997,2019).
The results of laboratory tests on intact and granulated marbles by Rosengren and Jaeger (1968), Gerogiannopoulos (1976) and Gerogiannopoulos and Brown (1978) are presented in Fig. 5. The UCS of the granulated marble(UCSd)is less than half of the intact marble strength (UCSi). The strength of the granulated marble rapidly increases with increasing confinement and approaches but never reaches that of the intact marble. At low confinement(σ3< UCSi/10), the strength envelopes of the granulated marble have equivalent friction angles (φe) between 55°and 65°. The equivalent friction angles (φeconsists of basic friction angle, φb,and dilation angle, i) of the intact marble for this range of confinement are between 35°and 48°. Beyond this confining pressure threshold (σ3≥UCSi/10), the strength envelopes have equivalent friction angles ranging between 10°and 32°for both intact and granulated marbles.
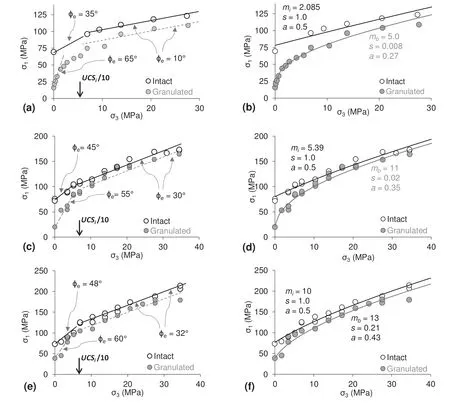
Fig.5. Triaxial strength data of intact and heat-treated (granulated) marbles and their confined strength matched using the HB strength parameters for:(a, b)Wombeyan marble reported by Rosengren and Jaeger (1968); (c, d) Wombeyan marble reported by Gerogiannopoulos (1976) and Gerogiannopoulos and Brown (1978); and (e, f) Carrara marble reported by Gerogiannopoulos (1976) and Gerogiannopoulos and Brown (1978).
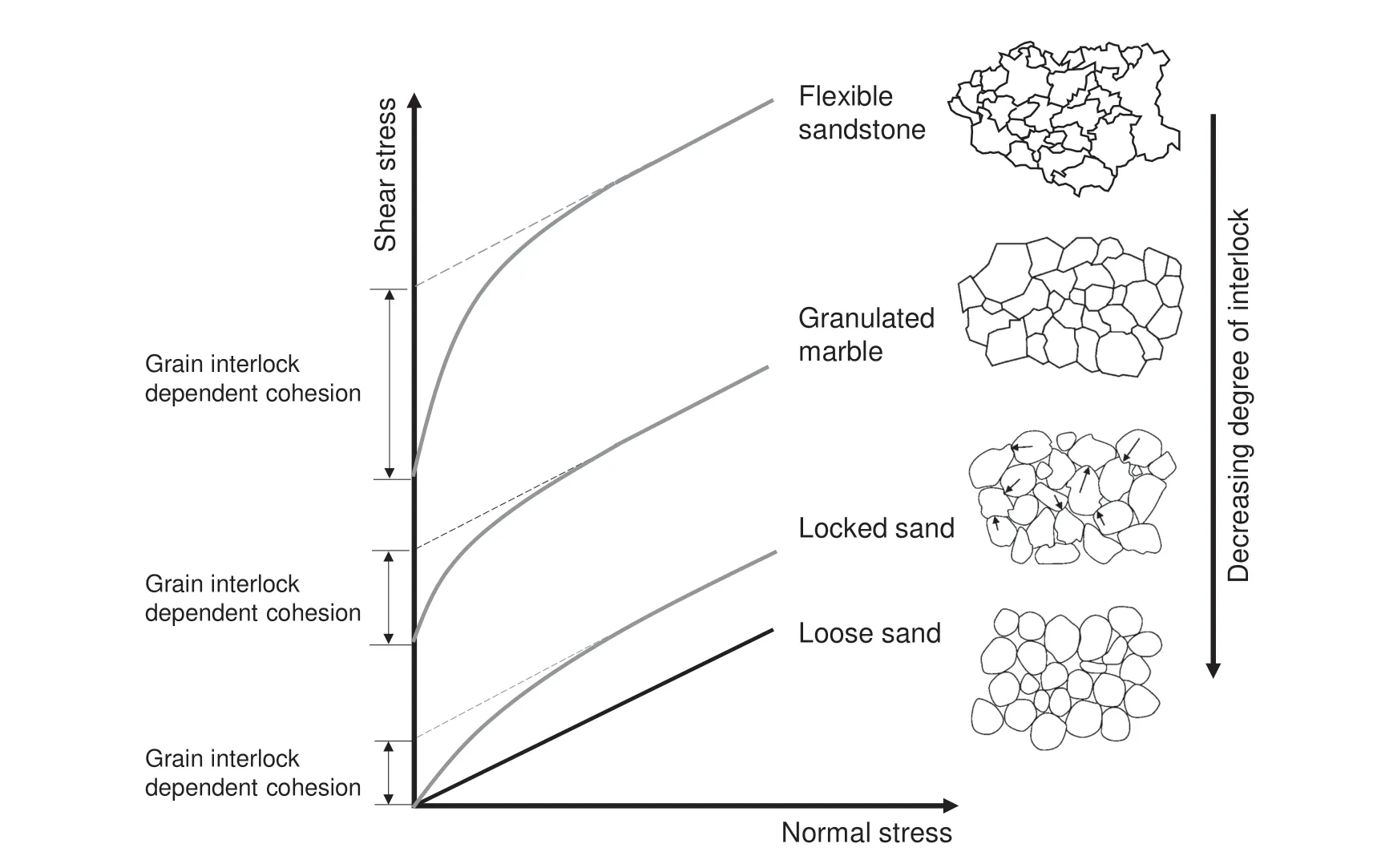
Bahrani and Kaiser (2013) analyzed the results of triaxial tests on heterogeneous(damaged and defected)rocks,including marble data presented in Fig. 5, as analogues for non-persistently jointed rock masses and suggested that a high value of mb, potentially exceeding mi(i.e. about 2.4 times higher than mi), and an a value smaller than 0.5 (i.e. about 0.38) will provide a better fit to the confined strength of such rock masses.The use of high m and low a values has also been suggested by Amann et al. (2012) to describe the strength of over-consolidated Opalinus clay. Fig. 5b, d, and f demonstrates how the confined strength of granulated marble is matched using the HB failure criterion by modifying the values of the GSI strength parameters mband a.In these figures,an mbvalue higher than miis used to capture a steep rise in the failure envelope at low confinement(σ3 The observed rapid increase in the strength of granulated marble with increasing confinement and its highly curved strength envelope is due to the tight and highly interlocked grain structure, the roughness of the grain boundaries and the corresponding high dilation at low confinement. Beyond a critical confinement (about UCSi/10 as shown in Fig. 5), dilation is suppressed due to shearing off the grain boundary asperities and breaking through the grains. Locked sand is a type of sand that is tightly compacted with concave grain boundaries providing extra interlock (Dusseault and Morgenstern, 1978, 1979). Locked sands have peak frictional strengths considerably in excess of those displayed by loose and dense sands due to their high dilation at low normal stress, which results in steeply curved failure envelopes (Fig. 6). Athabasca oil sands, Saint Peter sandstone in Minneapolis, and Swan River sandstone in Manitoba are examples of locked sands. Field evidence indicating high strength of oil sands includes natural oil sand slopes of 65 m high at slope angles of up to 55°.According to Dusseault and Morgenstern(1978,1979),slopes less than 65 m high and sections of some other slopes have also been observed to exist at steeper inclinations(e.g.slope height less than 15 m with angles of up to 90°). Fig. 6. Shear-box test results on oil sand showing envelopes for peak and residual strengths (after Dusseault and Morgenstern,1978,1979). The grain structure of the locked sand was suggested by Dusseault and Morgenstern (1978,1979) to be responsible for the observed behavior in the laboratory and the field. Locked sands have an apparent cohesion of about 140 kPa due to the high degree of grain interlock although they lack true cohesion at zero normal stress due to the lack of cement between the grains(fresh oil sand can be remolded readily in the hand) (see Fig. 6). The tight grain structure of oil sand consisting of interpenetrative fabric and long grain contacts results in high rates of dilation at low normal stresses.With increasing normal stress,the dilatancy is suppressed in favor of grain and grain boundary asperity shearing,resulting in a curved shear strength envelope, as depicted in Fig. 6. Itacolumite or flexible sandstone is another example of an analogue for a highly interlocked jointed rock mass (Dusseault,1980). This type of sandstone can move freely over a limited arc,then locks, and displays only elastic behavior. Dusseault (1980)reported on the laboratory beam-bending tests conducted on itacolumite slabs. He observed a large mid-point deflection with inelastic stress-strain curve and strain-stiffening behavior during most of the loading range. Such an unusual behavior was also observed upon torsion and axial tension-compression. Through the observation of thin sections and scanning electron microscope images taken from Indian and American itacolumite specimens, Dusseault (1980) concluded that individual quartz grains are physically separate (i.e. no infilling mineral), and intensely interdigitated with pyramidal overgrowths projecting into corresponding gaps in adjoining grains.This resulted in a high tensile strength of the material, but the individual grains can be easily rubbed off a corner.Itacolumite was suggested by Dusseault(1980) to display highly curvilinear failure envelope due to fabric cohesion, as opposed to intergranular cementitious cohesion,arising from its angular and interdigitated quartz grains and the corresponding dilation. Granulated marble, locked sand and flexible sandstone have several important similarities: a lack of cement between mineral grains and highly curvilinear failure envelopes as a result of high degree of interlock between their grains. Fig. 7 compares the schematic strength envelopes and fabrics of grain assemblies for flexible sandstone,granulated marble,locked sand and loose sand,showing a decreasing degree of interlock with decreasing grain irregularity,surface roughness,and increasing porosity.In all cases,dilatancy at low normal stresses(or low confinement)is large and suppressed in favor of grain and grain boundary asperity shearing at larger normal stresses (or high confinement). Note that the higher the degree of interlock, the higher the curvature of the strength envelope at low normal stress, and the higher the grain interlock-dependent cohesion. Similar behavior (i.e. high curvilinearity of failure envelope)is expected in highly interlocked jointed rock masses, which have a significant block interlock-dependent(apparent)cohesion,as reported by Patton(1966)and Ladanyi and Archambault (1970). This behavior is investigated using a grainbased distinct element modeling methodology in the following sections. Fig. 7. Schematic failure envelopes for flexible sandstone, granulated marble, locked sand and loose sand (modified after Dusseault,1980) and fabric of granular assemblies with decreasing degree of interlock from top to bottom: Flexible sandstone (drawn from Dusseault,1980), granulated Wombeyan marble with a porosity of less than 4% (drawn from Rosengren and Jaeger,1968),locked sand with a porosity of 27%-33%,with interpenetrative contacts indicated by arrows(after Dusseault,1980),and densely packed rounded sand with a porosity of 31%-34% (after Dusseault,1980). Fig. 8. (a) Grain-based model of Wombeyan marble; and (b) Correspondence between the strengths of laboratory and numerical specimens of intact and granulated marbles(Bahrani et al., 2014). Parallel bonds inside the grains are not shown in Fig. 8a. A numerical approach based on the distinct element method was used by Bahrani et al. (2014) to simulate the laboratory behavior of intact and granulated Wombeyan marbles reported by Gerogiannopoulos(1976)and Gerogiannopoulos and Brown(1978)(Fig.5c).This model was generated using the two-dimensional(2D)particle flow code (PFC) and its embedded grain-based modeling(GBM)methodology developed by Potyondy (2010). In the GBM, a rock specimen is simulated with its polygonal deformable and breakable grains. The grain-internal material (base material) is represented by several circular particles interacting through a parallel bond logic (Potyondy and Cundall, 2004), and the grain boundaries are simulated using the smooth-joint contact logic(Pierce et al., 2007). The parallel bonds are assigned a tensile strength and cohesion. Therefore, the grains, simulated as an assembly of several particles bonded together using parallel bonds,are cohesive. Once a parallel bond breaks, the displacement field and the transition to the residual strength are controlled by particle geometry and friction at particle-particle contact.Fig.8a shows the GBM used to simulate Wombeyan marble,and Fig.8b presents the calibration results, indicating excellent correspondence between the strengths of intact and granulated Wombeyan marbles from laboratory tests and those obtained from the calibrated GBMs.The average grain size of Wombeyan marble is between 1 mm and 2 mm (Rosengren and Jaeger,1968; Gerogiannopoulos,1976). The GBM constructed by Bahrani et al. (2014) had a simple grain structure consisting of two different-sized polygonal grains with average sizes of 1 mm and 2 mm that were randomly distributed within the specimen (see Fig. 8a). The calibration procedure and detailed results were described by Bahrani et al. (2014). In the following sections, the calibrated GBM of granulated Wombeyan marble is used as an analogue of a highly interlocked jointed rock mass. The cohesive grains and frictional grain boundaries represent rock blocks and joints, respectively. This calibrated grain-based model is then modified to investigate various factors contributing to the degree of interlock (e.g. block shape, joint persistence and joint surface condition)and therefore to variations in rock mass strength. Block shape or block geometry is one of the main factors controlling the degree of freedom for rock blocks to slide and rotate.Two rock mass structures (block geometries) were chosen to investigate the influence of block shape on the strength of jointed rock masses: polygonal blocks representing a highly interlocked jointed rock mass and rectangular blocks representing a rock mass with persistent joints (see Fig. 9). The models shown in Fig.9 are both analogue for jointed rock masses as they are of identical size.In PFC(and in general in DEM),the model size has no influence on the simulation results as long as the number of particles and joints,the size of particles and the size of blocks relative to the model size are kept constant. Two important parameters that should be considered when upscaling a numerical model are the joint stiffness and loading rate. As demonstrated by Bahrani and Kaiser (2016), when changing the model size, the loading rate should be adjusted until the macroproperties of the model become independent of the model size;the larger the model,the lower the strain rate.Based on the above discussion, it is suggested that if the analogue rock mass models shown in Fig. 9 are scaled up to 2 m × 5 m or 20 m × 50 m, the simulation results in terms of the strength and deformation properties will be comparable to those obtained in this investigation, as long as the joint stiffness and loading rate are properly adjusted. The structure of the synthetic rock mass (SRM) specimen with polygonal blocks is the same as the grain-based model of Wombeyan marble (Fig. 8a). Due to the shape of the blocks, this SRM specimen serves as an analogue for a ‘highly interlocked’ jointed rock mass and is referred to as RMHIhere.The structure of the SRM specimen with rectangular blocks formed by continuous joints is similar to a blocky rock mass(see GSI chart by Hoek et al.,1995 in Fig.4).Due to the shape of the blocks,this SRM specimen serves as an analogue for a ‘well interlocked’ jointed rock mass and is referred to as RMWIherein. Fig. 9. Two rock mass structures representing: (a) A highly interlocked, nonpersistently jointed rock mass (RMHI); and (b) A well interlocked, persistently jointed rock mass (RMWI). The specimen width is 20 mm in both models. The structures of the two SRM specimens are comparable in the sense that the blocks in both cases are formed by continuous block boundaries, i.e. the joints are all connected and do not terminate within intact rock.However, the main difference between the two structures is that the block boundaries in the RMHIspecimen are randomly oriented, therefore no single well-defined continuous joint set is formed(i.e.the‘joints’are non-persistent),whereas the RMWIspecimen consists of two well-defined persistent joint sets that extend entirely through the model. Fig. 10 presents the distributions of block boundary orientations in the RMHIand RMWIspecimens. The RMWIspecimen has two distinct block boundary orientations(i.e.40°and 140°from vertical).In the RMHIspecimen,the block boundary orientations are relatively uniformly distributed from zero to 180°from vertical, and therefore, no obvious preferential orientation can be identified for this model. Fig. 10. Distributions of block boundary orientations in analogues RMHI and RMWI models. The properties of the intact rock blocks and the joints in these SRM specimens are the same as those of the grain-based model calibrated to the properties of granulated Wombeyan marble(Table 1).This means that the joints are simulated as frictional,nondilatant contacts with an effective friction angle of 50°and zero tensile strength and cohesion. The bonded particle model without smooth joints(representing a massive rock mass)has an intact UCS of 118 MPa.The dip angles of the two joint sets in the RMWIspecimen were chosen so that the joints are inclined but not parallel to the direction of critical shear stress on joints (not at 45°+ φj/2 = 60°, where φjis the joint friction angle). The spacing between the joints in the RMWIspecimen was chosen so that the number of smooth-joint contacts is comparable to that in the RMHIspecimen;the RMHIand RMWIspecimens consist of 8286 and 8384 smoothjoint contacts, respectively. By choosing the same properties for the intact rock and the joints and similar numbers of smooth-joint contacts in these SRM specimens, the block shape is the only variable, and its influence on the rock mass strength can be established. Fig. 11a presents the peak strength envelopes of the highly interlocked rock mass (RMHI) and the well interlocked rock mass(RMWI)under unconfined and confined conditions.The UCS of the RMHIspecimen is about 20 MPa whereas it is about 1 MPa for RMWI.The confined strength increases nonlinearly with a high initial equivalent friction angle of φe=58°for RMHIand slightly less at 55°for RMWI, respectively. The equivalent friction angle gradually decreases with increasing confining pressure.For confining pressures greater than 10 MPa, the strength can be represented by a linear failure envelope with a friction angle of 28°for RMHIand 29°for RMWI, respectively. Fig.11b shows the change in the equivalent friction angle(φe)for different ranges of confining pressures for the two SRM specimens.For the highly interlocked rock mass (RMHI) specimen, the change in the equivalent friction angle with increasing confinement is gradual; it decreases from 58°for the confining pressure range of 0-3.4 MPa to 22°for the confining pressure range of 27.6-34.5 MPa. In the case of well interlocked rock mass (RMWI) specimen, the equivalent friction angle initially decreases at a slower rate at low confinement (σ3< 10.3 MPa) from 55°to 50°. It then drops to 34°for the confining pressure range of 10.3-13.7 MPa,and eventually decreases to 30°at the confining pressure range of 27.6-34.5 MPa. As shown in Fig.11,the main difference between the two SRM specimens is their strengths and strength developments at low confinement(σ3<10.3 MPa).The strength envelope of the highly interlocked rock mass specimen is nonlinear whereas that of the well interlocked rock mass specimen is bilinear. Due to the difference in geometries of the constituent blocks, the degrees of interlock and the dilational behavior differ at low confinement.This was further investigated by analyzing the types and patterns of intra-block fracturing at different levels of confinements. For this purpose, the numbers of intra-block tensile and shear fractures at the peak strength in both SRM specimens are compared in Fig.12. In the RMHIspecimen, intra-block tensile fracturing dominates the failure at all confining pressures, and intra-block shear fracturing starts at low confining pressures. The number of fractures(shear or tensile) prior to the peak strength increases with increasing confinement.On the contrary,in the RMWIspecimen,no intra-block fracturing occurs at confinement of zero to about 10 MPa, indicating that failure occurs by sliding along frictional joints.Minor intra-block tensile fracturing occurs at confinement of 6.9 MPa, and shear fracturing occurs only at high confining pressures (i.e. 27.6 MPa and 34.5 MPa). A further comparison of Figs.11 and 12 indicates that the nonlinearity of the strength envelope is controlled by the tensile cracking of the blocks, which occurs prior to the peak strength. In the RMHIspecimen where the strength envelope is nonlinear, the intra-block tensile cracking occurs at all confining pressures. As shown in Fig.11b,the equivalent friction angle decreases graduallywith increasing confining pressure.In the RMWIspecimen,the two sections of the bilinear strength envelope and the corresponding equivalent friction angles (i.e. Fig. 11a) correspond well with the observed intra-block tensile cracking.No tensile cracking occurs at confining pressures covering the first section of the bilinear envelope represented by an equivalent friction angle of 55°. Tensile cracking occurs at confining pressures greater than 10 MPa, corresponding to the second section of the bilinear envelope, represented by an equivalent friction angle of 29°. Table 1 Properties of blocks (balls and parallel bonds) and joints (smooth joints) in RMHI and RMWI specimens (after Bahrani et al., 2014). The evolving fracture patterns in the RMHIand RMWIspecimens are presented inFig.13 at five confining pressures(note thatslipof the frictional joints is not shown).In the RMHIspecimen,two dense‘shear zones’are generated by the interaction of intra-block tensile fractures at high confining pressures.First signs of localization are evident at 13.8 MPa confinement,and a continuous‘shear zone’is established at 34.5 MPa confinement. In the RMWIspecimen, ‘shear zones’ formation is more disperse and is not yet fully developed at 34.5 MPa confining pressure. Sliding along frictional joints (not shown)dominates the failure of thewell interlocked rock mass specimen for a wide range of confining pressures(0 MPa<σ3<20.7 MPa). Further insight into the failure modes of the two SRM specimens was obtained by analyzing the particle velocity vectors at selected locations inside the specimens at low (σ3= 3.5 MPa) and high(σ3=34.5 MPa)confining pressures,as illustrated by Fig.14: (1) Low confinement(σ3<10.3 MPa).At confining pressures less than 10.3 MPa, failure involves opening of block boundaries leading to dilation in the highly interlocked rock mass(RMHI)specimen. The direction of velocity vectors indicates movements of the blocks nearly perpendicular to the loading direction. At 3.5 MPa confining pressure, minor intra-block fracturing results in the generation of small shear planes. In the well interlocked rock mass (RMWI) specimen, failure involves a combination of sliding along block boundaries and block rotation. No intra-block fracturing occurs in the RMWIspecimen at 0 MPa and 3.5 MPa confining pressures. Fig.11. (a) Comparison between the strengths of highly interlocked (RMHI) and well interlocked (RMWI) rock mass specimens; and (b) Comparison between equivalent friction angles (φe) of RMHI and RMWI specimens for different ranges of confining pressures. Fig. 12. Numbers of intra-block tensile and shear fractures prior to reaching the peak strengths in (a) highly interlocked (RMHI) and (b) well interlocked (RMWI) rock mass specimens. Fig.13. Comparison of intra-block fracturing patterns in the RMHI and RMWI specimens up to their peak strengths for different values of confining pressures.Boxed areas in the top figures are zoomed in and shown in the lower figures.Green lines represent the frictional block boundaries(smooth-joint contacts);and red and blue lines represent the intra-block tensile and shear fractures (i.e. broken parallel bonds), respectively. (2) High confinement (σ3>10.3 MPa). At confining pressures greater than 10.3 MPa, the accumulation and interaction of intra-block tensile and shear fractures result in the formation of major shear fractures in the highly interlocked rock mass(RMHI) specimen. In the well interlocked rock mass (RMWI)specimen,a combination of sliding along frictional joints and tensile fracturing through the blocks drives the rock mass to failure. At 34.5 MPa confining pressure, the directions of velocity vectors in both SRM specimens are dominated by the intra-block fractures rather than the frictional joints. In summary, the block geometric interlock influences the strength development at low confinement because of different inter- and intra-block failure modes. The higher the block geometric interlock, the larger the strength at low confinement. Fig.14. Comparison of failure modes of RMHI and RMWI specimens at low and high confining pressures.Frictional joints and velocity vectors are shown with green lines and gray arrows, respectively. Fig.15. Examples of a massive jointed rock mass model (K′ = 0), a persistently jointed rock mass model (K′ = 1), and a non-persistently jointed rock mass model (K′ = 0.5). Blue circles refer to the locations of parallel bonds and black lines refer to the frictional smooth-joint contacts, respectively. The persistence describes the areal extent or size of a discontinuity within a plane.It influences the strength and failure modes of a jointed rock mass under different loading conditions.As discussed by Einstein (1993), instability is more likely to occur if joints are fully persistent. The presence of rock bridges in a non-persistently jointed rock mass prevents rock blocks from rotating or sliding and falling from an excavation or slope until the rock bridges have failed. As discussed earlier, the joint persistence influences the degree of interlock in a jointed rock mass, and it decreases with increasing joint persistence. In this section, the influence of joint persistence on the strength of the RMHIand RMWIspecimens is investigated. The SRM specimens were modified to simulate massive and non-persistently jointed rock masses. A massive rock mass was simulated by removing all smooth-joint contacts (i.e. block boundaries)and replacing them with parallel bonds with identical properties as used to bond the particles inside the blocks.Similarly,a non-persistently jointed rock mass was simulated by randomly removing a number of smooth-joint contacts and replacing them with parallel bonds. Fig.15 shows three examples: a massive rock mass where all the contacts are bonded using parallel bonds (locations of parallel bonds are indicated by blue circles), a fully persistently jointed rock mass where the block boundaries are simulated using smooth-joint contacts (black lines), and a nonpersistently jointed rock mass where 50% of the smooth-joint contacts are replaced with parallel bonds. The K′ratio refers to as the ratio of the number of smooth-joint contacts in a non-persistently jointed rock mass specimen to the total number of smooth-joint contacts in the persistently jointed rock mass specimen.As an example,the step-by-step procedure to construct a non-persistently jointed rock mass specimen with a K′ratio of 0.5 (right image in Fig.15) is described below: Fig.16. Examples of RMHI and RMWI specimens with non-persistent(K′ <1)and persistent(K′ =1)joints.Black lines are smooth-joint contacts.Parallel bonds inside the blocks are not shown. Fig. 17. Influence of K′ ratio (joint persistence) on UCSs of highly interlocked (RMHI)and well interlocked (RMWI) rock mass specimens. (1) All the smooth-joint contacts in the fully persistently jointed rock mass specimen were first identified. (2) 50% of these smooth-joint contacts were randomly deleted from the specimen. (3) The particle-particle contacts whose smooth-joint contacts were removed in the previous step were identified. (4) Parallel bonds with properties identical to those between the particles inside the blocks were added to the contacts identified in the previous step. Various levels of joint persistence in a jointed rock mass were simulated by varying K′from 0 to 1 with increment of 0.1,following the procedure described above.Fig.16 shows examples of RMHIand RMWIspecimens with non-persistent and persistent joints. The UCSs of the RMHIand RMWIspecimens as a function of K′ratio are presented in Fig. 17. The UCS of the massive rock mass(K′=0)is about 118 MPa.This is equal to the lower bound strength of calcite grain,which has a UCS of between 120 MPa and 150 MPa(Lama and Vutukuri,1978). Note that calcite grains in granulated marble serve as an analogue for homogeneous rock blocks in a jointed rock mass. The UCS values of both RMHIand RMWIspecimens decrease nonlinearly with increasing K′ratio or joint persistence. The respective strengths are comparable for K′ratios less than 0.5. For higher K′ratios, the strength of the RMWIspecimen decreases more rapidly,as slip along joints occurs more easily as the structure of the RMWIspecimen approaches a persistently jointed rock mass (K′= 1). The RMHIspecimen retains more than 50% of the UCS till K′>0.8. It also has a UCS of about 20 MPa at K′= 1. Fig.18. Influence of joint persistence (K′ ratio) on the confined strength of: (a) highly interlocked (RMHI) and (b) well interlocked (RMWI) jointed rock mass specimens. The influence of joint persistence on the failure envelope or confined strength of RMHIand RMWIspecimens is illustrated in Fig.18.The strengths of RMHIand RMWIspecimens are comparable at high confinement (σ3>10 MPa) because intra-block fracturing dominates and joint slip is inhibited due to the combined influence of confinement and block boundary interlock arising from the relatively high friction angle of the joints (i.e. 50°). The main difference between the two SRM specimens is their strengths at low confinement (σ3<10 MPa) and for K′ratios greater than 0.5. The RMHIspecimen exhibits higher strength due to higher dilation caused by the shape of the blocks.In other words,as the rock mass structure approaches a persistently jointed rock mass(K′=1), the influence of slip along joints dominates the failure of the RMWIspecimen at low confinement (σ3< 10 MPa), making it a weaker material than the RMHIspecimen. The joint surface condition has a fundamental influence on the shear strength of rock joints. Factors controlling the joint surface condition include the joint roughness(i.e.JRC in the Barton-Bandis joint shear strength criterion) and the joint wall compressive strength (i.e. JCS in the Barton-Bandis joint shear strength criterion)(Barton,1973).The joint surface condition controls the degree of interlock along the joints (i.e. block boundary interlock). The degree of interlock increases with increasing joint roughness and wall compressive strength. In the calibration of the grain-based model of Wombeyan marble and for the simulation of jointed rock masses, the joint roughness was not explicitly simulated,as the smooth joint logic in PFC considers joints as smooth surfaces.To account for varying joint surface conditions and specifically to consider the added resistance due to joint roughness,the smooth joint friction angle in the jointed rock mass models was increased from its basic friction angle(φj)to the ‘equivalent’ friction angle (φj+ i), where i represents the joint dilation angle. For example, the joints in the RMHIand RMWIspecimens were assigned an equivalent joint friction angle of 50°.This represents a rough joint,which has a basic friction angle of 35°and a dilation angle of 15°.Strictly speaking,this only takes a part of the effect of joint roughness into account, which is the increase in strength but not the normal deformation,as it still is a smooth joint.Hence,the actual effect of joint roughness on dilation is higher than what is simulated here. The influence of the ‘equivalent’ joint friction on the strengths of the RMHIand RMWIspecimens is illustrated in Fig. 19. Fig. 19a shows that a reduction in joint equivalent friction angle from 50°to 20°reduces the UCS of the RMHIspecimen from about 20 MPa to nearly zero. The strength envelopes of all RMHIspecimens are nonlinear,independent of the value of joint friction angle.This is because the shape of the blocks prevents sliding along joints without intra-block fracturing even with a low joint friction angle. The UCS of the RMWIspecimen is nearly zero for all values of joint friction angle(Fig.19b),but the confined strength of the RMWIspecimen is strongly controlled by the smooth joint friction angle,and the confined strength decreases much more rapidly with decreasing joint friction compared to that of RMHIspecimens. The bilinear shape of the strength envelope vanishes with decreasing joint friction. The strength envelopes of the RMWIspecimens with friction angles greater than 40°are bilinear and become linear for lower joint friction angles(shown for 29°and 20°).The linearity of the strength envelopes of the RMWIspecimens with low joint friction angles is interpreted to be due to the freedom of the rock blocks to slide along persistent joints. It is concluded from the results presented in Fig.19 that the shear strength of the joints has much less effect on the confined strength of highly interlocked jointed rock masses with randomly oriented joints than that on the well interlocked jointed rock masses with well-defined persistent joint sets. In summary, the condition of block forming joints plays a dominant role in the confined strength and failure mode of blocky rock masses but much less in moderately or non-persistently jointed rock masses. As discussed earlier, the initial development of the HB failure criterion was based on the results of triaxial tests on Panguna andesite.Hoek and Brown(1980)also analyzed triaxial test data of Westerly granite (Wawersik and Brace,1971) and intact and granulated (heat-treated) Wombeyan marbles (Rosengren and Jaeger,1968; Gerogiannopoulos,1976) during the development of the HB failure criterion.For Westerly granite,they used different post-peak fracturing stages representing jointed rock masses of various qualities and determined their HB strength parameters.They found that the values of the HB strength parameters m and s decrease as fracturing of Westerly granite progresses;the value of m is reduced from mito mbby a factor of about 2, and the value of s decreases from 1 to 0 as the strength of granite is reduced from the peak to the ultimate. For Wombeyan marble, they found that the value of the constant s dropped from 1 for the intact marble to 0.19 for the granulated marble, whereas the value of the constant m increased from mi= 4 for the intact marble to mb= 5.26 for the granulated marble. Fig.19. Influence of joint equivalent friction angle on the confined strength of (a) highly interlocked (RMHI) and (b) well interlocked (RMWI) jointed rock mass specimens. Sj Phi denotes the smooth joint friction angle. Hoek and Brown (1980) discussed that after granulation, the calcite grain became the basic unit of the granulated marble,which would be expected to have a higher value of σcithan the intact(not heat-treated)marble.They hypothesized that if the unconfined and confined strengths of calcite crystals could have been measured and analyzed as the intact rock analogue,the value of mbfor granulated marble(rock mass analogue)would have been determined to be less than 5.26.Furthermore,they noted that the observed increase in the value of m, which is against the trend of the results of Panguna andesite and Westerly granite,could likely be due to the high degree of geometric interlock caused by the shape of calcite grains and the roughness of their grain boundaries. They further discussed that such a high degree of interlock would exist in very massive rock at considerable depth below ground surface. For these reasons, they suggested that the granulated marble would not be a reasonable analogue for moderately to poorly interlocked jointed rock masses such as the heavily jointed and weathered Panguna andesite.Therefore, they used neither the results of laboratory tests on Wombeyan marble in the development of the HB failure criterion nor the GSI strength equations.This suggests that the applicability of the GSI strength equations must be limited to strength estimation of moderately to poorly interlocked jointed rock masses. For this reason, the limitations of the GSI strength equations(Eqs. (2)-(4)) for estimating the confined strength of interlocked rock masses are investigated in this section. For this purpose, the HB failure criterion (Eq. (1)) with GSI = 100 was first fitted to the strength of the massive rock mass model(i.e.PFC specimen where all particles were bonded with parallel bonds;K′=0 in Fig.15).The GSI was then lowered until the reduced UCS matched those of RMHIand RMWIspecimens with fully persistent joints (K′= 1). This analysis was conducted for different values of smooth joint friction angle for both SRM specimens. Fig. 20 presents the results of this analysis for the highly interlocked rock mass(RMHI)specimen with smooth joint friction angles of 50°and 20°. The HB failure envelopes obtained with the GSI strength equations anchored at the UCS of the RMHIspecimen consistently underestimate its confined strengths independent of the value of joint friction angle.The simulated strength is up to two times higher than that obtained from the GSI strength equations.This is attributed to the fact that the GSI strength equations for determination of HB strength parameters were not developed for the estimation of the confined strength of highly interlocked jointed rock masses as reviewed above. The results for the well interlocked rock mass(RMWI)specimens with fully persistent joints for various smooth joint friction angles(50°-20°) are presented in Fig. 21. It is found that the UCS of the RMWIspecimen can be matched with GSI = 20 for all the cases,because its strength is independent of the smooth joint friction angle under the unconfined condition. However, the GSI strength equations again consistently underestimate the confined strength of the RMWIspecimen for joint friction angles of 50°-30°,and the confined strength of the RMWIspecimen decreases and approaches that estimated by the GSI approach as the joint friction angle decreases to 30°. The confined strength estimated by the GSI approach matches that of the RMWIspecimen at a joint friction angle of 20°. Fig. 20. Comparison between the confined strength of rock masses estimated using the GSI approach and those of highly interlocked jointed rock mass (RMHI) models having smooth joint friction angles (SJ Phi) of (a) 50° and (b) 20°. Fig.21. Comparison between the confined strengths estimated using the GSI approach and those of well interlocked rock mass for different smooth joint friction angles (SJ Phi) of 50°, 40°, 30° and 20°. The main difference between Panguna andesite jointed rock mass described earlier and the simulated RMWIspecimen is the rock block conditions. The Panguna andesite rock blocks are heavily disturbed and much weaker than the intact andesite specimens tested in the laboratory (Fig. 3a). The joint surface in this rock mass is also heavily weathered (Hoek and Brown,1980)and must have had a relatively low friction angle. The strength envelopes estimated using the GSI strength equations match that of the RMWIspecimen only when the smooth joints in the RMWIspecimen are assigned a very low friction angle (Fig. 21). This suggests that the GSI strength equations can only be used to properly estimate the confined rock mass strength in well interlocked, persistently jointed rock masses consisting of hard brittle rock blocks,if the block boundaries are smooth and free to move. It is concluded from these analyses that the GSI strength equations are not applicable to highly and well interlocked jointed rock masses consisting of hard brittle rock blocks bound with dilatant joints.However,the GSI strength equations can be used to estimate the confined strength of well interlocked,persistently jointed hard rock masses when the joint surfaces are non-dilatant and smooth. The influence of the degree of interlock on rock mass strength was recognized during the early development stages of the HB failure criterion and later introduced into the GSI system. The determination of this parameter and therefore the GSI value for a jointed rock mass are challenging and subjective. In an effort to make the determination of the GSI value for a jointed rock mass more objective, Cai et al. (2004) replaced the degree of block interlock in the GSI system with the block size or block volume.In this study,it is shown how the strengths of the two analogous rock mass models,having similar block sizes,can vary,especially at low confinement. The two analogous rock mass models represent two extreme cases in terms of the degree of block interlock in blocky hard rock masses. In the highly interlocked rock mass model, the rock mass consists of polygonal blocks, where joints forming the blocks terminate on other joints but are not continuous and therefore do not generate planes of weakness throughout the model. An example of a highly interlocked jointed rock mass with a similar block geometry is a rock with columnar jointing, which often develops in basalt and dolerites.In columnar jointed rock masses,the medium is divided into columns that are typically hexagonal with side lengths in the order of a few tens of centimeters.The columns are also usually intersected by cross joints that become less regular with depth (Jaeger et al., 2007). In such rock masses, the columns can slide along their long axis yet, due to the high degree of interlock between these columns in the direction perpendicular to their long axis, they cannot rotate or slide without disrupting the rock mass fabric or breaking through the intact rock. In the well interlocked rock mass model,the rock mass consists of two continuous joint sets or planes of weakness with a constant joint spacing. In this case, the failure of the rock mass involves sliding along the joints at low confinement, and a combination of block rotation and intra-block failure at higher confinement.Therefore, the strength envelopes of the two analogous rock mass models exhibit different levels of nonlinearity. The highly interlocked rock mass model exhibits a nonlinear strength envelope with a continuously changing slope, whereas the well interlocked rock mass model shows a bilinear strength envelope, suggesting two distinct failure mechanisms at low and high confinements.Future studies could consider an intermediate case to better understand the influence of the degree of block interlock on the failure mechanism and the peak strength of jointed rock masses at various levels of confinement. The HB failure criterion and the GSI system were developed to provide a simple approach to estimate the strength of jointed rock masses and to provide input to continuum-based numerical models. In practice, the challenge is to determine the degree of interlock for a jointed rock mass, especially in underground excavations. The modeling results presented in this article offer a first contribution to assist in this challenging task.Future studies should be conducted towards better quantification of the degree of block interlock for a jointed rock mass. Discrete fracture network(DFN)models are powerful tools that can be used as an aid to explicitly account for the presence of discontinuities and construct various degrees of block interlock based on the data obtained from geological field mapping, and core and borehole logging. The integration of the DFN into numerical models to generate SRM models allows for a better understanding of the failure process and strength and deformation properties of rock masses at various scales (e.g. Grenon and Hadjigeorgiou, 2003; Mas Ivars et al., 2011; Farahmand et al.,2018). The GBM is a type of SRM that is now implemented in various numerical programs based on finite element, discrete element and hybrid finite-discrete element methods such as RS2(Bewick et al.,2012),universal distinct element code(UDEC)(e.g.Lan et al., 2010; Gao and Stead, 2014; Sinha and Walton, 2020),PFC(e.g.Potyondy,2010;Bahrani et al.,2014;Liu et al.,2018),and Irazu (Abdelaziz et al., 2018). This modeling approach, as demonstrated in this paper, allows creating polygonal blocks to simulate heterogeneities at various scales.The investigation of the influence of block interlock on rock mass strength in this study was limited to two dimensions. With the rapid increase in the computation power, it is also possible to create blocks of various shapes in three dimensions, e.g. using the bonded block model(BBM) implemented in 3DEC (e.g. Garza-Cruz et al., 2014;Ghazvinian et al., 2014). The challenge in all these numerical methods is the lack of calibrated model input properties; therefore, an iterative model calibration is usually adopted. As discussed by Bahrani et al.(2014) and Sinha and Walton (2020), and demonstrated by Bahrani and Hadjigeorgiou (2018), the number of unknowns in the necessary input parameters for these models (i.e. SRM, GBM,and BBM) is often more than the knowns. Therefore, more than one combination of input properties can lead to a ‘calibrated’model for a given loading condition. However, this ‘calibrated’model may not necessarily be valid for a different loading condition or stress path. For example, a GBM or a BBM calibrated to the strength of a rock under an unconfined condition may not properly estimate (i.e. underestimate or overestimate) the confined strength of the rock. This poses a major challenge when estimating the confined strength of jointed rock masses,which is relevant for the design of pillars in deep mines, using the SRM modeling approach.This is because the calibration of SRM models is usually conducted based on the observation of rock mass failure near the tunnel walls,where the confinement is relatively low(i.e.in the range of a few megapascals). In such situations, integrated investigations of rock mass behavior through geological mapping,field observation, and deformation and seismic/micro-seismic monitoring provide valuable data to improve model calibration,resulting in a more reliable predictive tool for forward analysis and excavation design. A grain-based model previously calibrated to the laboratory properties of Wombeyan marble was extended to simulate highly and well interlocked jointed rock masses to investigate factors contributing to the degree of interlock in a jointed rock mass,including block shape,joint surface condition and joint persistence. The highly interlocked rock mass model consisted of polygonal blocks and the well interlocked rock mass consisted of two nearly orthogonally persistent joint sets.The SRM specimens consisted of hard brittle homogeneous rock blocks,having a block UCS of about 118 MPa, joints with zero tensile strength and cohesion, and a relatively high equivalent friction angle of 50°.It was found that the main difference between the two rock mass specimens is their strength and failure mechanisms at low confinement(i.e.σ3 (1) Unconfined condition. The highly interlocked rock mass specimen fails at a peak stress of about 20 MPa,whereas the strength of well interlocked rock mass specimen is only 1 MPa. (2) Low confinement (σ3< 10.3 MPa). The highly interlocked rock mass represents a higher strength at low confinement compared to the well interlocked rock mass. Its failure involves opening of blocks at their boundaries as well as some intra-block fracturing. The well interlocked rock mass fails mainly due to sliding of blocks along their frictional boundaries. (3) High confinement (σ3>10.3 MPa). The strengths of highly interlocked and well interlocked rock masses at high confinement are comparable, as the slip along the joints is inhibited and failure occurs due to intra-block fracturing.Their failures involve intra-block fracturing, although this is more dominant in the highly interlocked rock mass. Various levels of joint persistence were simulated in both rock mass models. It was found that the strengths (unconfined and confined) of highly interlocked and well interlocked rock mass decrease as the level of joint persistence increases. Moreover, the nonlinearity of the strength envelope in both rock masses increases with increasing persistence (K′) as complete blocks with fully persistent joints are formed. The influence of joint surface condition (friction angle) on rock mass strength was investigated by varying the joint friction angle from 50°for rough and dilatant joints to 20°representing smooth and non-dilatant joints. It was found that the nonlinearity of the strength envelope of the highly interlocked rock mass is not affected by the joint friction. On the other hand, the joint friction angle influences the nonlinearity of the strength envelope in the well interlocked rock mass,and the strength envelope is bilinear for joint friction angles greater than 30°and becomes linear for lower joint friction angles. The results of the numerical simulations showed that the strength of non-persistently jointed and blocky hard rock masses(i.e. for GSI >65) is strongly dependent on the degree of interlock and in general higher than that predicted by the GSI strength equations.A more accurate strength estimation of such rock masses can be achieved only if factors such as the shape of rock blocks,joint roughness and joint persistence are considered. It was demonstrated that the HB failure criterion should not be used to estimate the strength of non-persistently jointed and blocky hard rock masses(GSI >65).The HB failure criterion may be used to estimate the confined strength of well interlocked persistently jointed rock masses consisting of hard rock blocks,only if the joints are smooth and non-dilatant. The results presented in this paper highlight the need for revised criteria for estimation of the confined peak strength of nonpersistently jointed and blocky hard rock masses. Declaration of competing interest The authors confirm that there are no known conflicts of interest associated with this publication, and there has been no significant financial support for this work that could have influenced its outcome. Acknowledgments This research was supported by the Natural Sciences and Engineering Research Council of Canada, MIRARCO Mining Innovation,the Center for Excellence in Mining Innovation (CEMI), and Itasca Consulting Group. The authors wish to thank Dr. Evert Hoek for sharing his notes on the historical development of the HB failure criterion including laboratory test data on Panguna andesite and acknowledge his many constructive comments and suggestions during the conduct of the research reported here.4.2. Locked sand

4.3. Flexible sandstone

5. Simulation of rock masses of various degrees of block interlock
5.1. Influence of block shape




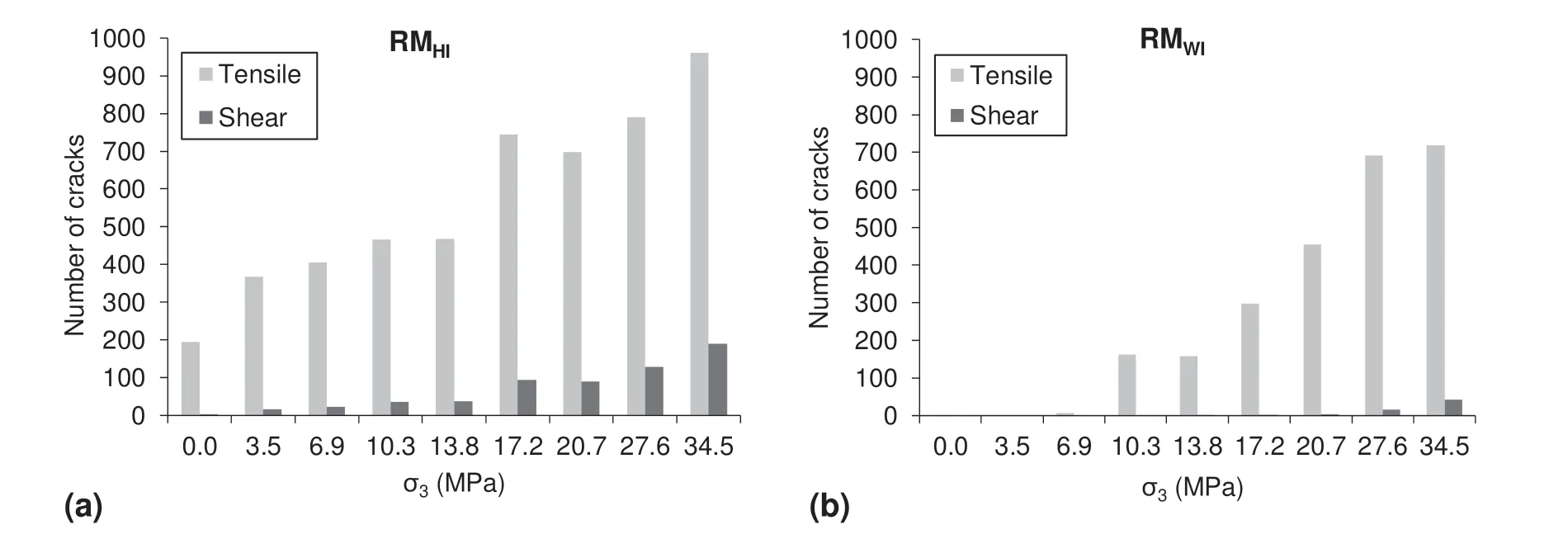

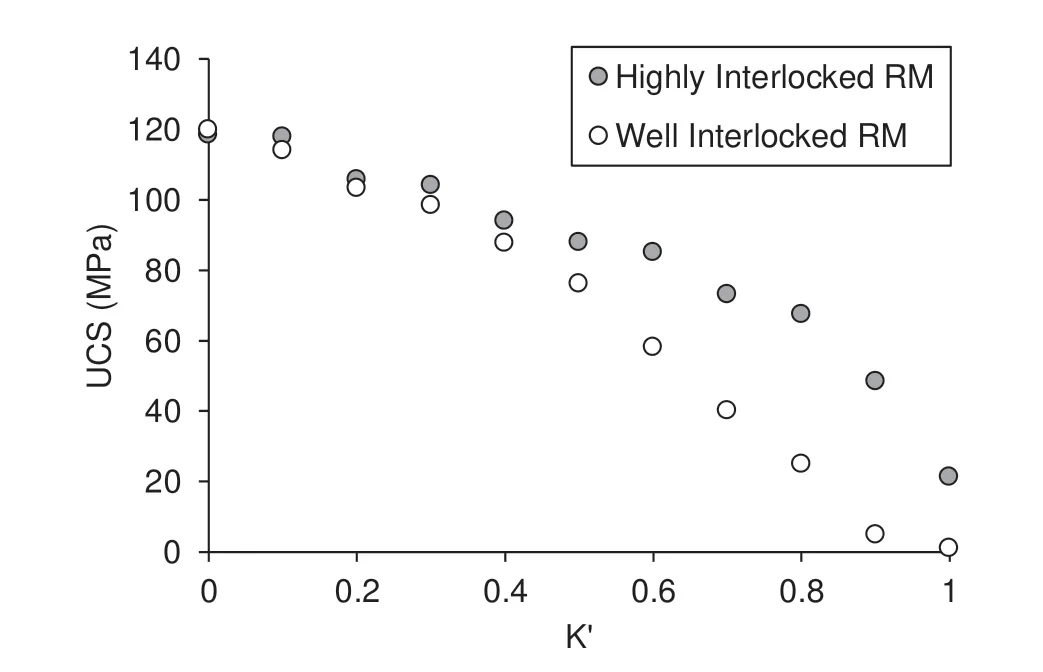
5.2. Influence of joint persistence



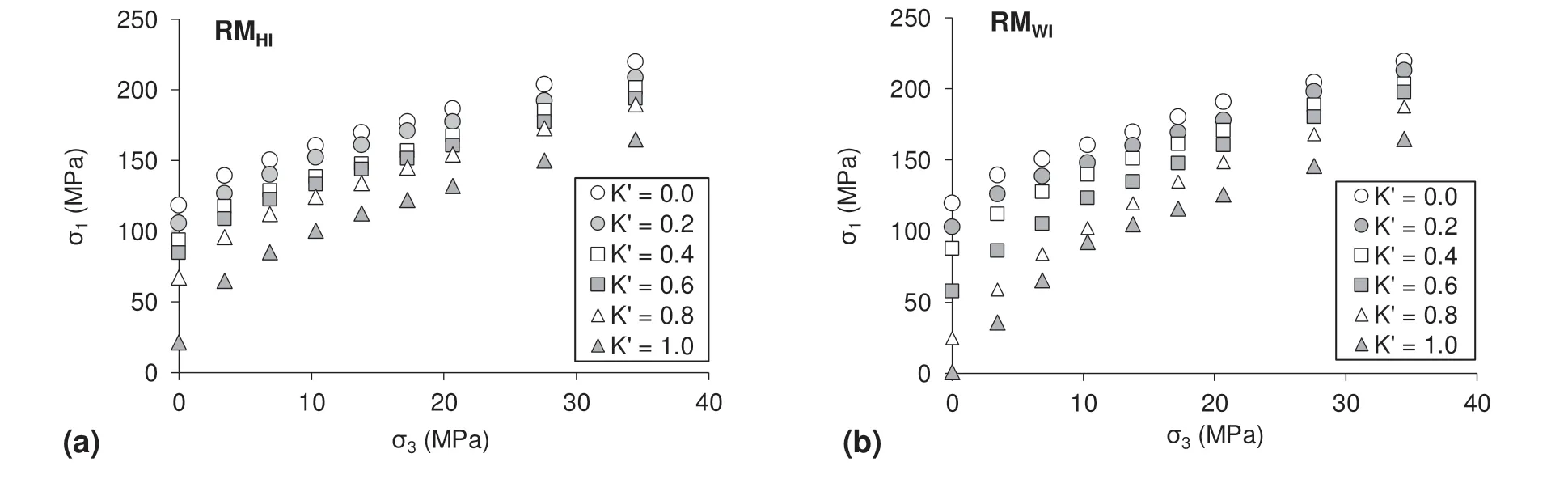
5.3. Influence of joint surface condition
6. Limitations of applicability of GSI strength equations for blocky hard rock masses



7. Discussion
8. Summary and conclusions
 Journal of Rock Mechanics and Geotechnical Engineering2020年6期
Journal of Rock Mechanics and Geotechnical Engineering2020年6期
