Performance analysis of empirical models for predicting rock mass deformation modulus using regression and Bayesian methods

Adeyemi Emman Aladejare, Musa Adeayo Idris

a Oulu Mining School, University of Oulu, Oulu, Finland

b Division of Mining and Geotechnical Engineering, Department of Civil, Environmental and Natural Resources Engineering, Luleå University of Technology, Luleå,Sweden

Keywords:Deformation modulus Rock mass Regression equation Bayesian method Performance analysis Rock mass rating (RMR)

A B S T R A C T Deformation modulus of rock mass is one of the input parameters to most rock engineering designs and constructions.The field tests for determination of deformation modulus are cumbersome,expensive and time-consuming. This has prompted the development of various regression equations to estimate deformation modulus from results of rock mass classifications,with rock mass rating(RMR)being one of the frequently used classifications.The regression equations are of different types ranging from linear to nonlinear functions like power and exponential. Bayesian method has recently been developed to incorporate regression equations into a Bayesian framework to provide better estimates of geotechnical properties.The question of whether Bayesian method improves the estimation of geotechnical properties in all circumstances remains open. Therefore, a comparative study was conducted to assess the performances of regression and Bayesian methods when they are used to characterize deformation modulus from the same set of RMR data obtained from two project sites.The study also investigated the performance of different types of regression equations in estimation of the deformation modulus.Statistics, probability distributions and prediction indicators were used to assess the performances of regression and Bayesian methods and different types of regression equations. It was found that power and exponential types of regression equations provide a better estimate than linear regression equations.In addition, it was discovered that the ability of the Bayesian method to provide better estimates of deformation modulus than regression method depends on the quality and quantity of input data as well as the type of the regression equation.

1. Introduction

Design of engineering structures such as rock foundations,slopes, and other underground openings in or on a rock mass requires adequate information on the geotechnical properties of the rock mass,most notably the deformation modulus(Em),as they help to understand the rock mass response to external perturbations(Aladejare and Wang,2019a,b).In addition,adequate knowledge of Emwill enable safe and cost-effective design of the engineering structures. Since rock mass comprises of intact rock blocks separated by tightly interlocking discontinuities, the properties of the intact rock cannot represent, directly, the properties of the rock mass. Hence, to determine the properties of the rock mass such as Em, empirical or experimental methods are usually utilized (Shen et al., 2012; Idris et al., 2013). Experimental methods such as in situ tests are expensive and time-consuming.Besides, the experimental method requires a test drift, which may not be available at the preliminary stage of the design. Therefore,empirical methods are often used to estimate rock mass properties indirectly because they are simple and cost-effective. Several researchers have proposed different empirical models to estimate the values of Embased on the rock mass classification systems(Gokceoglu et al.,2003;Khabbazi et al., 2013;Kavur et al., 2015).

The common rock classification systems are rock quality designation (RQD) (Deere et al., 1967), rock mass rating (RMR)(Bieniawski,1976,1989), tunneling quality index (Q) (Barton et al.,1974; Barton, 2002), geological strength index (GSI) (Hoek et al.,1995, 1998), and rock mass index (RMi) (Palmström, 1996a,b).Among the rock mass classification systems that are used to estimate Em, RMR has been the most investigated. This is one of the reasons for numerous empirical models relating RMR to Emin the literature (e.g. Gokceoglu et al., 2003; Isik et al., 2008; Khabbazi et al., 2013; Nejati et al., 2014; Karaman et al., 2015). These empirical models are developed using different databases and assumptions(Alemdag et al.,2016;Panthee et al.,2018).As shown in Fig. 1, the estimation of rock properties involves different uncertainties. The data of rock properties used in the rock mass classification systems often have inherent variability (Stille and Palmström, 2003; Palmstrom and Stille, 2007; Idris, 2014;Aladejare, 2016; Aladejare and Wang, 2017a). The inherent variability is the actual variability because rocks are natural materials,and their properties vary spatially and are affected by various geological processes that they have undergone in their geological histories (Wang et al., 2016a). During the determination of the input data for the rock mass classification systems using in situ or laboratory tests,measurement errors and statistical uncertainty are added to the inherent variability already present in the rock properties (Phoon and Kulhawy, 1999a; Wang and Aladejare,2016a). Measurement errors include both systematic bias and random errors associated with the measurement process used,while statistical uncertainty occurs when statistical inference is made based on some samples, rather than all samples, of a population(Wang et al.,2016a).When regression equations are used to estimate rock mass properties such as the case of Emfrom RMR,transformation uncertainty, which is due to the simplification in the regression models (Phoon and Kulhawy, 1999b; Aladejare,2020), is added to the variability and uncertainties already present in the RMR data. All these variability and uncertainties then propagate through the RMR data and regression equation to the estimated Em. Using information from such estimates in rock engineering practice may lead to a misleading design and analysis,which is often the cause for the disparity between the expected and actual performances of rock structures like tunnels, foundations and open pit. Therefore, there is a need to explicitly model the uncertainties,especially when using a regression model to estimate Em. Such modeling can be accomplished using Bayesian method(Wang and Aladejare, 2016b; Aladejare and Wang, 2017b; Asem and Gardoni, 2019).

Bayesian approach has recently been used in rock mechanics to explicitly model the uncertainties in intact rock properties (Wang and Aladejare, 2015, 2016a,b; Aladejare and Wang, 2018; Asem and Gardoni, 2019). Fattahi and Ilghani (2019) used Bayesian method to identify the most appropriate models to predict Emamong several candidate models using data of four different parameters including RMR. Feng and Jimenez (2015) selected the most appropriate model, among four commonly used models, to estimate Embased on its RMR or GSI values. However, the two studies mainly focused on identifying appropriate models and updating the model parameters for estimation of Em.No study has been reported to directly investigate the suitability of incorporating regressions between RMR and Eminto Bayesian framework, by comparing the performance of the Bayesian method to regression method. Therefore, the objective of this paper is to assess the performance of regression equations for predicting Emwhen they are used directly and/or incorporated into Bayesian frameworks.This paper presents a comparative study between the regression and Bayesian approaches when they are used to characterize Emfrom the same set of RMR data obtained at a project site. In addition,the study seeks to assess the performance of different types of regression equations and infer the suitability of different types of regressions for estimation of Em. Firstly, a review of existing regression models for estimating Emfrom RMR data was briefly presented, followed by discussion on prediction indicators for regression equations. The prediction analysis was performed to select regression equations with good performances. A Bayesian framework was presented and incorporated with the selected regression equations to improve the estimations from the regression equations. Data from two sources were used to illustrate the effect of incorporating regression models into Bayesian method and to establish whether it leads to better estimation of Em.

2. Regression models for estimating rock mass deformation modulus

The in situ determination of Emhas remained one of the most daunting tasks in the field of rock mechanics because of the associated practical and economic difficulties(Zhang and Einstein,2004;Edelbro et al.,2007).Therefore,many empirical models are proposed, based on rock mass classification system and related intact rock properties such as intact rock strength and modulus(e.g.Hoek and Diederichs,2006;Karaman et al.,2015).Among the various rock mass classification systems,RMR is one of the widely used classifications (Zhang et al., 2019). The RMR value can be obtained from six cumulative ratings of the classification parameters, which are the ratings of the uniaxial compressive strength(UCS) of intact rock, RQD, spacing of discontinuities, condition of discontinuities, groundwater conditions and orientation of discontinuities relative to the tunnel alignment. The ratings of the parameters are contained in the guideline by Bieniawski (1989).Although other rock mass classification systems are also used for rock engineering designs such as GSI, the RMR system is considered in this study due to the possibility to consider the interactions of the classification parameters and its wide acceptance and usage. Researchers have developed many empirical models based on the RMR to estimate Em. Table 1 presents some of the regression equations proposed by different researchers to estimate Emusing the RMR classification system.Note that not all the regression models for estimating Emfrom RMR are listed in Table 1. Table 1 mainly lists the regression equations used in this study to investigate the performance of regression equations during prediction of Em.

Fig.1. Uncertainties propagation through regression estimation of rock properties (modified after Phoon and Kulhawy,1999a).

Table 1 Some RMR-based empirical equations for estimating rock mass deformation modulus.

3. Prediction indicators for regression models

Absolute average relative error percentage (AAREP), F statistic(F), root mean square error (RMSE) and R-squared (R2) were adopted in this study as indicators to assess the reliability of prediction by regression equations:

where N is the number of testing data used;var(.)is the variance;Emimesand Emiestare the deformation moduli of rock masses obtained from the in situ data and derived from the regression equations,respectively;andandare the mean values of Emobtained from the in situ data and estimated from the regression equations, respectively.

AAREP is used to judge the prediction accuracy of a model or method, by computing the relative error between measured and predicted values. RMSE is the standard deviation of the errors associated with the estimation if it is unbiased. Therefore, the smaller the AAREP and RMSE,the more reliable the estimation.R2is the proportion of the variance in the output variable that the model can predict from the input variable.The F statistic was used in this study to compare the variances of two data sets(i.e.measured and estimated values)and evaluate the quality of regressions.Contrary to AAREP and RMSE, the larger the R2and F, the more reliable the estimation and vice versa.

4. Bayesian method

Estimations of many rock mass properties typically make use of regressions to quantify the relationship between measured and predicted variables. In this study, Emwas predicted using RMR variables and regression equations. As regression equations are developed through data fitting for a specific site, there is an error in using such models for rock property estimation(Ditlevsen,1981; Wang and Aladejare,2016b). This uncertainty is not accounted for when regression models are directly used to estimate Em.In this section,a Bayesian framework is presented to infer and update the estimates of Emfrom regression equations by incorporating state of existing knowledge about Emand explicitly modeling the uncertainties arising from estimation of Em.

Consider the regression equations used in Section 3 for examples, which are used to estimate Emwhen it cannot be measured directly. Generally, values of Emestimated from the regression equations can be simply written as a function of RMR as

where f（RMR;εR）represents a functional relationship between Emand RMR, and εRis a random variable representing the transformation uncertainty or modeling error associated with each regression equation (Phoon and Kulhawy, 1999b; Asem and Gardoni, 2019). Using the Bayesian framework, the updated knowledge on Emcan be expressed as posterior distribution based on RMR data and prior knowledge/information about Em. In a Bayesian framework,the site data and the prior probability density function (PDF) for the model parameters of Emare updated according to the following updating rule(Wang and Aladejare,2015,2016a,b; Aladejare and Wang, 2017b; Aladejare et al., 2020) as

where fII（Em） is the posterior PDF that represents the updated knowledge about Em, K is a normalizing factor that ensures that fII（Em） is a proper PDF, L（Em） is the likelihood function which relates the RMR data with regression equation,and fI（Em）is the prior PDF which reflects expertise’ knowledge on Embefore observed data become available. fI（Em） can be assumed as a joint uniform distribution of the distribution parameters of Em,such as the mean μ and standard deviation σ.The likelihood function L（Em）is the PDF of site observation data RMR for a given set of model parameters μ and σ(i.e.L（Em） = P（RMR|μ， σ）).It probabilistically quantifies the information of μ and σ provided by RMR. Likelihood model is derived to probabilistically relate(μ,σ)to RMR.Then,the likelihood function is formulated according to the likelihood model.The exact formulation of the likelihood function depends on the function of each regression equation, and how the values of Emare estimated using RMR data.

As the resulting PDF from Eq. (6) is often complicated and difficult to express analytically (Wang and Aladejare, 2015; Asem and Gardoni, 2019; Fattahi and Ilghani, 2019), a Markov chain Monte Carlo (MCMC) simulation technique is used to numerically solve the resulting PDF.The MCMC simulation was used to simulate a sequence of samples of Emas a Markov chain with the PDF of Emas the Markov chain’s limiting stationary distribution (Fattahi and Ilghani, 2019). The samples simulated after the Markov chain reaches its stationary condition are taken as the samples of Em. The simulated samples reflect the posterior knowledge of Em,which is an integrated knowledge of prior information and RMR data.From a statistical point of view,the samples simulated from the posterior distribution of Emthrough MCMC are equivalent to those Emdata obtained from laboratory tests for the same site. The step-by-step algorithm and implementation of MCMC simulation from such complicated PDF have been reported in Wang and Cao (2013) and Wang and Aladejare(2016a).In addition,the entire process of using Bayesian method to update and simulate samples of Emcan be performed using Bayesian equivalent sample toolkit (BEST)(Wang et al.,2016b).BEST is an Excel add-in program for implementing the Bayesian equivalent sample method. Users only need to supply basic information like regression model, input data, set of prior information, number of desired simulations, and the add-in will return a specified simulation of desired rock property samples.

5. Illustrative examples

To assess the performances of empirical models for predicting Em,data from two case studies and the regression equations listed in Table 1 were used. Table 2 presents Emand RMR reported by Serafim and Pereira(1983)and re-presented by Barton(1995).The data were adopted for Case I in this study,and it consists of 15 data points of Emand RMR. Table 3 presents Emand RMR reported by Khabbazi et al. (2013). The data were adopted for Case II in this study,and it consists of 10 data points of Emand RMR.For the two cases, the data of RMR will be used with regression equations in Table 1 to estimate Em.The measured Emdata presented in Tables 2 and 3 are for validation, to compare the estimated Emfrom the regression equations with the measured Emfrom the site.

To estimate Emusing Bayesian approach,the selected regression equations from regression analysis together with RMR data and prior knowledge of Emwere incorporated into Bayesian framework.The prior knowledge of Emadopted in this example is the typical ranges of mean (μ) and standard deviation (σ) of Emwhich were compiled from the data and statistics of Emreported in the literature.The prior knowledge(i.e.fI（Em）)is quantitatively reflected by a joint uniform distribution with a μ value ranging from 1.1 GPa to 39.6 GPa and a σ value ranging from 1 GPa to 20 GPa (Gokceoglu et al., 2003; Aladejare and Wang, 2019a). The posterior PDF from the integration of regression equation, RMR data and prior knowledge is then incorporated into MCMC simulation to generate 10,000 samples in order to determine the statistics and probability distribution of Em.The performances of the regression analysis and Bayesian approach to estimate Emare discussed in the next subsections.

5.1. Performance of regression method

Using the RMR in Cases I and II (i.e. from Tables 2 and 3,respectively)and regression equations from Table 1,Emvalues are calculated. The calculation results of Emfor the two cases are presented in Tables 4 and 5.Table 4 contains the measured Emfor Case I and the estimated Emobtained using RMR data and the seven regression equations in Table 1. The table also includes the means and standard deviations estimated for the measured Emand the estimated Emfrom the seven regression equations in Table 1.For both mean and standard deviation,only the estimatesfrom the first and last regression equations in Table 1(Aydan et al.,1997; Read et al.,1999) are close to the mean and standard deviation of the measured Em.The estimates from other five regression equations in Table 1 significantly underestimate the mean and standard deviation of Em. The two regression equations that provide satisfactory statistics of the mean and standard deviation are power functions.This may indicate that the relationship between Emand RMR is nonlinear and are better represented in the form of power function. For Case II as presented in Table 5, the mean and standard deviation estimated from the fourth and sixth regression equations in Table 1(Gokceoglu et al.,2003;Khabbazi et al.,2013)are close to the mean and standard deviation of the measured Em.The estimates from some of other five regression equations significantly overestimate Em,while others underestimate Em.For Case II, a power and an exponential function provide satisfactory statistics of the mean and standard deviation. This further indicates that there is nonlinearity between Emand RMR. For both cases, no linear regression equation provides satisfactory estimates of the statistics of Em. This suggests that using linear regression to estimate Emfrom RMR may lead to underestimation or overestimation of Em.

Table 2 RMR and Em of Case I (After Serafim and Pereira,1983; Barton,1995).

Table 3 RMR and Em of Case II (after Khabbazi et al., 2013).

To further assess the performances of the regression equations,four prediction indicators were used. The analysis results are presented in Tables 6 and 7.For Case I in Table 6,regression equations of Read et al.(1999)and Aydan et al.(1997)show higher estimation accuracies compared to others. Both regression equations have AAREP values less than 50%, while other equations have AAREP greater than 50%. The two regression equations have F statistic values greater than 140, while other regression equations have F statistics of less than 1. For RMSE, the two regression equations have estimates less than 5 GPa,while others have RMSE estimates greater than 10 GPa. For R2, the two regression equations have values more than 92%, while others have slightly lower values.Since AAREP and RMSE accounts for the error in using regression equations for estimation of parameters, the lower the ARREP and RMSE, the better the predictive performance of regression equation. Therefore, the regression equations of Read et al. (1999) and Aydan et al. (1997) with the lowest values of AAREP and RMSE provide better estimates of Emthan other equations.Also,F statistic and R2are used to compare the similarity in the variances of two groups of estimates, the regression equations of Read et al. (1999)and Aydan et al. (1997) have the highest values of F statistic and R2with better estimates of Em.

For Case II,the regression equations of Khabbazi et al.(2013)and Gokceoglu et al. (2003) show higher estimation accuracies compared to others. Both regression equations have AAREP values less than 10%. The two regression equations have F statistic values greater than 200,while other regression equations have F statistics less than 100. For RMSE, the two regression equations have estimates less than 0.3 GPa.For R2,the two regression equations have values more than 98%, while other equations have slightly lowervalues.From the definitions of AAREP and RMSE,the results imply that Khabbazi et al. (2013) and Gokceoglu et al. (2003) with the lowest values of AAREP and RMSE provide better estimates of Emthan other equations. Also, the regression equations of Khabbazi et al. (2013) and Gokceoglu et al. (2003) having the highest values of F statistic and R2provide better estimates of Em.

Table 4 Data and statistics of Em for Case I.

Table 5 Data and statistics of Em for Case II.

Table 6 Prediction performance of different regression equations for Case I.

Table 7 Prediction performance of different regression equations for Case II.

5.2. Performance of Bayesian method

Using the two regression equations,which perform best in each case,with the RMR data and prior knowledge of Emin the Bayesian framework mathematically represented in Eq. (6), samples of Emwere simulated by MCMC. The statistics and probabilitydistribution of Emfrom the Bayesian approach were estimated to determine whether the incorporation of the regression equations into Bayesian framework leads to improved estimation of Emor not. Tables 8 and 9 show the mean and standard deviation of Emestimated from Bayesian approach for Cases I and II, respectively.In Table 8, it is observed that the Bayesian estimation of Emfor regression equations of Read et al. (1999) and Aydan et al. (1997)have smaller mean absolute differences. Also, the Bayesian estimation of Emfor regression equation of Aydan et al. (1997) have smaller standard deviation absolute difference while that of Read et al. (1999) is only slightly higher. This shows that incorporating the prior knowledge with regression equations and 15 RMR data in the Bayesian framework improves the estimates of Em.In Table 9,it is observed that the Bayesian estimation of Emfor regression equations of Khabbazi et al. (2013) and Gokceoglu et al. (2003)have higher mean absolute differences and standard deviation absolute differences. This shows that incorporating the prior knowledge with regression equations and 10 RMR data in the Bayesian framework does not improve the estimates of Emin Case II, as it causes the estimated Emto deviate further from the measured Em.

Table 8 Comparison of estimated Em from regression and Bayesian analyses with measured Em (Case I).

Table 9 Comparison of estimated Em from regression and Bayesian analyses with measured Em (Case II).

To further investigate the performance of the Bayesian method in estimation of Em, the cumulative distribution function (CDF)plots of the Emsamples estimated from regression and Bayesian methods are plotted and compared with the CDF of measured Emfor both cases in Figs.2 and 3.For both regression equations in Case I as shown in Fig. 2, the Bayesian method improves the distributions of estimated Emsamples.This makes the CDF plot of Emfrom the Bayesian method to be closer to that of the measured Em. It shows that the disparities between the measured and estimated Emusing only regression equations are significantly reduced by introduction of prior knowledge in the Bayesian method. For both regression equations in Case II as shown in Fig. 3, the Bayesian method does not provide any noticeable improvement to the distributions of estimated Emsamples. The difference in the performances of the Bayesian method as noticed in the two cases may be due to the quality and quantity of data or general prior knowledge used in the method.If the input data are not of good quality,it will affect the results from the Bayesian method, because it forms a substantial part of the inputs to the Bayesian method. When the input data are relatively small, estimates from Bayesian method may be dominated by prior knowledge,and if the prior knowledge used is not consistent with the data from the specific site, the results obtained from Bayesian method might be affected.

Fig. 2. Cumulative distribution plots for Case I: (a) Regression equation from Read et al. (1999), and (b) Regression equation from Aydan et al. (1997).

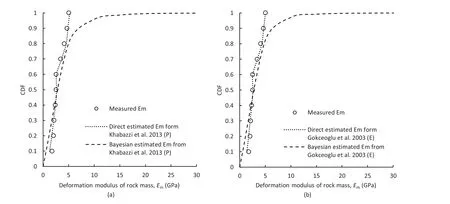
Fig. 3. Cumulative distribution plots for Case II: (a) Regression equation from Khabbazi et al. (2013), and (b) Regression equation from Gokceoglu et al. (2003).

Table 10 Comparison of Em estimated from regression and Bayesian method using different prior information for Case II.

6. Effect of prior knowledge on Bayesian method

The performance of Bayesian method obviously depends on the prior knowledge used in the Bayesian analysis(see Section 5.2).The results from Case I show that the Bayesian method performs better than regression method, whereas in Case II, the performance of Bayesian method is not convincing. The use of general prior knowledge may have influenced the performance of Bayesian method in Case II. Therefore, the prior knowledge should use, as much as possible, the information available from the specific site.When the prior knowledge used is not consistent with the data from the specific site,the results from Bayesian method might not be consistent with the measured data at the site(e.g.Case II).In this section, an improved prior knowledge is used by making use of other information available from Case II to develop an improved prior knowledge and to explore the effect of prior knowledge on the results from Bayesian analysis for Case II.

To incorporate the information from the site in Case II,the range of prior knowledge used in Section 5 is further reduced by taking the site-specific RMR information into consideration. The upper bound of the prior mean value of Emis reduced using the upper bound value of RMR from the site with general range of RMR (0-100) and the general range of prior mean value of Emby interpolation. This gives a new range of prior mean value of Emas 1.1-22.7 GPa.The range is reasonable,since the 10 available Emvalues also fall within the improved range of prior knowledge of Em. The six-sigma rule, which can be used to estimate the standard deviation of data when only a range of the data are available, is used to estimate the upper bound value of standard deviation as 3.6 GPa.On the other hand,the minimum standard deviation of Emis taken as 0 GPa because of the non-negative physical meaning of standard deviation. This set of ranges (i.e. μ ∈[1.1 GPa, 22.7 GPa] and σ ∈[0 GPa, 3.6 GPa]) is taken as the improved prior knowledge in this example.

Table 10 shows the results when the improved prior knowledge is used in Bayesian method, which are compared to the results obtained using regression method and when general prior knowledge(see Section 5)is used in Bayesian method.For both regression equations,using improved prior knowledge improves the estimates of mean and standard deviation of Em. The estimates of mean and standard deviation become more confident and consistent with the mean and standard deviation of the measured Emat the site. The relative differences in mean and standard deviation of Emreduced significantly when the prior knowledge was improved by considering information from the site. As the prior knowledge incorporates more information from the site, the estimates from Bayesian method become more consistent with the measured Emat the site. This indicates that the performance of Bayesian method can be greatly enhanced using improved prior knowledge which incorporates information from the site.

7. Conclusions

In this study, the performances of regression and Bayesian methods for estimation of Emwere investigated and illustrated,to assess the type of regression function suitable for estimation of Em.Besides, the study also assessed whether incorporating regression equations into Bayesian method leads to improvement in estimation of Em. The regression method makes use of regression equations and RMR data to estimate rock mass deformation modulus,while the Bayesian method uses the regression equations, RMR data and prior knowledge.Two cases(with 15 and 10 data of RMR,respectively) were used as illustrative examples to investigate the performances of the regression and Bayesian methods for estimation of rock mass deformation modulus.The following conclusions can be drawn from this study:

(1) There is a nonlinear relationship between Emand RMR.Therefore,using linear regression equations may not provide satisfactory estimates of rock mass deformation modulus from RMR data,since linear regressions may not capture the true nature of the relationship between the two rock mass properties of the same geological unit. Thus, it may be of advantage to use nonlinear regression functions like power and exponential regressions,when there is need to estimate rock mass deformation modulus from data of RMR. In this study, the power regression functions and one exponential regression function produced satisfactory estimates of Em.On the other hand, the estimates of rock mass deformation modulus from linear regression equations are not satisfactory.

(2) The performances of regression equations can differ considerably for the same input data. The fact that no regression equation produces satisfactory performance across the two illustrative cases shows that no regression equation can be taken as a universal model for empirical estimation of Emfrom RMR. Regression equations are developed using data from a geologic setting;therefore,they perform better when they are used to estimate Emof a site with a similar or very close geologic setting.

(3) Bayesian method can effectively enhance empirical estimation of Emfrom RMR. However, the results show that the performance of the Bayesian method for empirical estimation of Emdepends on the input data, regression equation and prior knowledge used in Bayesian framework. The performance of Bayesian method significantly depends on the prior knowledge used in the Bayesian analysis. Bayesian method benefits when the prior knowledge used is consistent with the data from the specific site.Therefore,the prior knowledge should use,as much as possible,the information available from the specific site.

Declaration of competing interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.